基于身份的可穿刺簽名方案

楊冬梅，陳越，魏江宏，胡學先

（信息工程大學數據與目標工程學院，河南 鄭州 450001）

1 引言

在基于公鑰基礎設施的密碼體制中，權威機構通過數字簽名為用戶頒發公鑰證書，保證了用戶公鑰的真實性和可信性。與此同時，用戶證書的頒發、存儲和撤銷以及認證核查等工作也帶來了繁重的管理開銷。為此，Shamir[1]在1984 年首次提出了基于身份的簽名（IBS,identity-based signature）方案，即以用戶的個人信息（如身份證號、手機號、電子郵箱地址等）作為其公鑰，而用戶私鑰由一個密鑰生成中心利用系統主密鑰來生成，簽名的驗證也只需要簽名用戶的公鑰對所對應的身份信息，從而避免了對公鑰基礎設施的依賴。

隨后，圍繞IBS 方案安全性增強、效率提升和功能擴展等方面，密碼學者提出了很多新的IBS 方案，如Cha[2]給出了完整的IBS 方案和該方案在隨機預言模型下的安全性證明，Paterson 等[3]在標準模型下構造了第一個高效的IBS 方案，楊小東等[4]提出了強不可偽造的基于身份服務器輔助驗證簽名方案，劉翔宇等[5]提出了第一個緊致安全的IBS 方案，田苗苗等[6]提出了格上基于身份的增量簽名方案以及侯紅霞等[7]提出了素數階群上基于非對稱對的身份基環簽名。在這些傳統的IBS 方案中，假設用戶私鑰都是絕對安全的。但在現實應用環境中，隨著網絡攻擊手段的多樣化，用戶私鑰泄露事件趨于高發。另一方面，一旦用戶私鑰被攻擊者竊取，攻擊者就可以產生任何消息的合法簽名，導致用戶之前生成的所有簽名都將失效。

為降低數字簽名方案中由私鑰泄露所帶來的損失，Anderson[8]在1997 年首次引入了前向安全數字簽名方案的概念，即要求在用戶私鑰泄露后，之前所生成的簽名是不能被偽造的，但他并沒有給出具體構造。Bellare 等[9]在1999 年的美密會上首次對這種密碼學原語進行了形式化定義，并基于RSA（Rivest Shamir Adleman）群上的整數分解問題給出了一個具體構造。隨后，學者對前向安全的數字簽名方案進行了大量而又深入的研究，提出了很多在安全性和效率方面具有各自優勢的相關方案，如Itkis 等[10]提出了具有高效簽名和驗證效率的前向安全簽名方案，Kozlov 等[11]給出了密鑰能快速更新的前向安全簽名方案，Libert 等[12]構造了不可信更新環境中前向安全的簽名方案，Abdalla 等[13]對文獻[9]方案的私鑰規模進行了優化等。以上這些前向安全的數字簽名方案均是基于公鑰證書的。為避免對公鑰基礎設施的依賴，Yu 等[14]在IBS 中引入了前向安全性，形式化地定義了前向安全的基于身份簽名方案，并給出了一個具體構造。

然而，如Green 等[15]所指出，上述傳統的通過周期性更新密鑰實現前向安全性的方法不夠靈活，導致其在實際部署中不可用。具體而言，傳統的前向安全IBS 方案[14]以固定的時間周期為單位（如每小時、每天等）更新用戶私鑰，這導致當前時間周期的私鑰泄露之后，攻擊者仍能偽造當前時間周期內的簽名。此外，傳統的前向安全IBS 方案采用二叉樹結構管理用戶密鑰和時間周期，使這些方案的密鑰更新效率較慢。

為克服已有前向安全IBS 方案在密鑰更新靈活性和效率方面存在的不足，本文提出了基于身份的可穿刺簽名（IBPS,identity-based puncturable signature）方案。這種新的簽名方案實現了細粒度的前向安全性，即每當用戶完成對某個消息的簽名之后，立即對私鑰進行更新，使更新后的私鑰不能再用來對同樣的消息進行簽名，保證了私鑰泄露之前所生成簽名的安全性。本文主要貢獻總結如下。

1) 對傳統的IBS機制進行了擴展，給出了IBPS機制的形式化定義，并通過安全模型刻畫了這種簽名方案的存在不可偽造性。

2) 將基于布隆過濾器的可穿刺公鑰密碼方案的構造思想應用到IBS，基于Paterson 等[3]的IBS方案構造了一個具體的IBPS 方案，其密鑰更新過程只需進行一次布隆過濾器中的元素刪除操作。

3) 基于計算性Diffie-Hellman（CDH,computational Diffie-Hellman）假設，在隨機預言模型下證明了所構造IBPS 方案滿足存在不可偽造性，并通過仿真實驗展示了方案的實際性能。

2 相關工作

Yu 等[14]基于Waters[16]提出的基于身份加密方案，利用二叉樹結構首次構造了前向安全的IBS 方案。在這種構造中，系統的生命周期被離散化為N個子周期，通過單向地周期性更新私鑰和刪除前一周期的私鑰，用戶可以在每個時間周期內使用不同的私鑰，從而實現了前向安全性。沿用類似的方法，魏江宏等[17]提出了前向安全的密文策略基于屬性加密方案；Wei 等[18]在前向安全IBS 的基礎上通過用戶撤銷引入了后向安全性；Oh 等[19]進一步考慮了系統主密鑰泄露的問題，提出了能同時抵抗用戶私鑰泄露和系統主密鑰泄露的IBS 方案；楊小東等[20]在標準模型下提出了可撤銷的基于身份的代理重簽名方案。

事實上，上述方案的構造方法在一定程度上源于前向安全的公鑰加密方案[21]，因此也就繼承了其局限性。為實現更實用的細粒度前向安全性，Green等[15]提出了可穿刺公鑰加密方案的概念，并基于支持非單調訪問結構的基于屬性加密方案構造了具體的可穿刺公鑰加密方案。隨后，Wei 等[22]構造了密文長度固定的可穿刺的基于身份加密方案。為提高可穿刺加密方案中私鑰穿刺的效率，Derler 等[23]進一步提出了布隆過濾器加密方案，并基于不同密碼學原語給出了多種構造方案。

類似于可穿刺的公鑰加密方案，可穿刺簽名方案同樣能提供簽名的細粒度前向安全性，由Bellare等[24]首次提出。但是，他們給出的通用構造依賴于不可區分混淆和單向函數，具有較高的計算開銷，在實際中不可用。Halevi 等[25]雖然也提出了一個可穿刺簽名方案，但是需要在私鑰穿刺操作后更新公鑰，帶來了較大的公鑰管理負擔。Li 等[26]基于布隆過濾器加密方案構造了具有較高穿刺效率的可穿刺簽名方案，并將其應用到了區塊鏈中的權益證明協議。

3 預備知識

3.1 布隆過濾器

布隆過濾器[27]是一種經典的隨機數據結構，通過一個簡短的二進制序列T來表示一個集合S，并能高效地判定一個元素s是否屬于該集合。具體而言，在集合S 上進行查詢時，若s∈S，則以概率1 返回1，表示s確實在集合S 中；若s?S，則以概率1-δ返回0，表示s不在集合S 中，其中δ為假陽性概率，即當s?S 時，仍以δ的概率返回1。

定義1布隆過濾器[27]。令U 為元素取值空間，其上的布隆過濾器 B=(BFGen,BFUpdate,BFCheck) 由3 個子算法組成，具體定義如下。

BFGen (?,k)，生成算法。以2個正整數 ?,k∈N為輸入，首先選擇k個一般的Hash 函數H1,…,Hk，其中Hj:U→[ ?]，并令（長度為? 且各個位置均為0 的字符串），最后輸出(H,T)。

BFUpdate (H,T,u)，更新算法。以Hash 函數族過濾器當前狀態T∈{0,1}?和一個元素u∈U 為輸入，首先令T′←T，然后對任意的整數j∈ [k]，令T′[H j(u)]=1，其中T′[i]表示T′的第i位，最后返回更新后的過濾器狀態T′。

BFCheck (H,T,u)，檢驗算法。同樣以Hash函數族過濾器的當前狀態T∈{0,1}?和一個元素u∈U 為輸入，然后計算并輸出一個比特

如上定義的布隆過濾器具有完善的完備性、假陽性概率有界、集合表示緊致等特性。

3.2 雙線性映射與CDH 假設

定義2雙線性映射。令G 和GT是2 個階為p的乘法循環群，其中p是一個長度為λ（安全參數）的素數，令g為G 的隨機生成元，則雙線性映射e:G × G →GT滿足下述條件的映射。

1) 雙線性：對任意的群元素x,y∈G 和任意的整數a,b∈Zp，e(x a,yb)=e(x,y)ab均成立。

2) 非退化性：e(g,g) ≠ 1。

3) 可計算性：對任意的群元素x,y∈G，存在一個多項式時間算法能有效計算出e(x,y)。

為方便描述，用一個五元組 (G,GT,g,p,e)來表示如上定義的雙線性映射。進一步，定義在群G 上的CDH 問題是指，給定群元素g a,gb∈G，要求計算gab，其中是隨機選取的整數。

定義3CDH 假設。對于任意一個概率多項式時間的攻擊者A，給定g a,gb∈G，若其輸出gab的概率是λ的可忽略函數，則稱CDH 假設在群G 上成立。

4 可穿刺的IBS 方案定義

4.1 形式化定義

IBPS 方案可看作一般的IBS 方案在安全性方面的增強，也可看作可穿刺簽名方案針對無公鑰基礎設施情形下的擴展。粗略而言，可穿刺的簽名方案比一般簽名方案多了一個私鑰穿刺算法，即當用戶的私鑰在每簽名完一個消息后，需要利用該消息在用戶私鑰上進行穿刺操作，以防用戶私鑰被再次用來產生該消息的簽名。

通過結合一般的IBS 方案[3]和可穿刺加密/簽名方案[23,26]的形式化定義，下面給出IBPS 方案的形式化定義，共由5 個多項式時間的算法組成。

Setup()λ，系統建立算法。輸入系統安全參數λ，輸出系統公開參數pp 和系統主密鑰msk。

Extract(pp,msk,ID)，私鑰提取算法。輸入系統公開參數pp、系統主密鑰msk 和用戶身份ID，輸出相應的初始私鑰skID。

Punc(pp,skID,m)，私鑰穿刺算法。輸入系統公開參數pp、用戶的當前私鑰skID和一個用該私鑰簽名過的消息m，輸出一個更新過的私鑰sk′ID，此時也稱sk′ID是被消息m穿刺過的私鑰。

Sign(pp,skID,m)，簽名算法。輸入系統公開參數pp、用戶當前私鑰skID和待簽名消息m，輸出對消息m的簽名σ。

Verify(pp,σ,m,ID)，驗證算法。輸入系統公開參數pp、簽名σ、簽名消息m和用戶身份ID，當σ是一個關于ID 和m的有效簽名時輸出1，否則輸出0。

一個IBPS 方案是正確的是指，對任意按正確方式生成的公開參數和主密鑰(pp,msk)←Setup(λ)、任意用戶初始私鑰skID←Extract (pp,msk,ID)以及任意簽名消息集M={m1,…,mq}和簽名消息m∈M，有

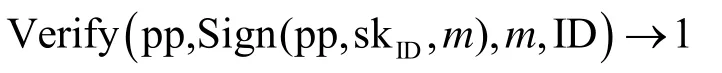
總成立。對反復穿刺q次后的用戶私鑰Punc(pp,skID,mi)(i∈ [q])，只要簽名消息m?M，則

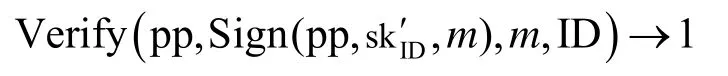
總成立。

4.2 安全性定義

為定義IBPS 方案的存在不可偽造性，在安全模型中給攻擊者提供了私鑰提取詢問、簽名詢問和私鑰穿刺詢問。此外，為刻畫前向安全性，還允許攻擊者詢問挑戰者身份所對應的私鑰，但所返回的私鑰必須是被挑戰消息穿刺過的。具體而言，IBPS方案的存在不可偽造性通過一個挑戰者C 和一個敵手A 之間的安全游戲來定義，主要包含以下3 個階段。

系統建立階段。給定安全參數λ，挑戰者C 運行系統建立算法Setup(λ)→(pp,msk)，然后將系統公開參數pp 發送給敵手A，而自己持有系統主密鑰msk。同時，挑戰者C 初始化4 個空集

詢問階段。在該階段，敵手A 可以自適應地進行以下3 種詢問。

1) 私鑰提取詢問。敵手A 向挑戰者C 提交一個用戶身份ID，要求挑戰者C 返回相應的私鑰skID。接收到該詢問后，挑戰者C 直接運行私鑰提取算法Extract(pp,ms k,ID)→skID，同時更新集合Qsk←Qsk∪{ID}，然后將skID發送給敵手A。

2) 簽名詢問。敵手A 向挑戰者C 提交一個用戶身份ID 和消息m，要求挑戰者C 返回相應的簽名σ。挑戰者C 首先調用私鑰生成算法Extract(pp,msk,ID) →skID，然后運行簽名算法Sign(pp,skID,m)→σ，同時更新集合Qsig←Qsig∪{(ID,m)}和Qσ←Qσ∪{σ}，最后將簽名 發送給敵手A。

3) 穿刺詢問。敵手A 向挑戰者C 提交一個用戶身份ID 和消息m，要求挑戰者C 返回相應被m穿刺過的用戶私鑰為此，挑戰者首先通過調用私鑰生成算法產生用戶的初始私鑰，即Extract(pp,ms k,ID)→skID，然后調用私鑰穿刺算法Punc(pp,skID,m)→同時更 新集合Qpunc←Qpunc∪{(ID,m)}，最后將穿刺過后的私鑰sk′ID發送給敵手A。

偽造階段。敵手A 結束詢問階段之后，輸出一個關于(m*,ID*)的簽名σ*。

若以下條件同時滿足，則稱敵手A 贏得了上述安全性游戲。

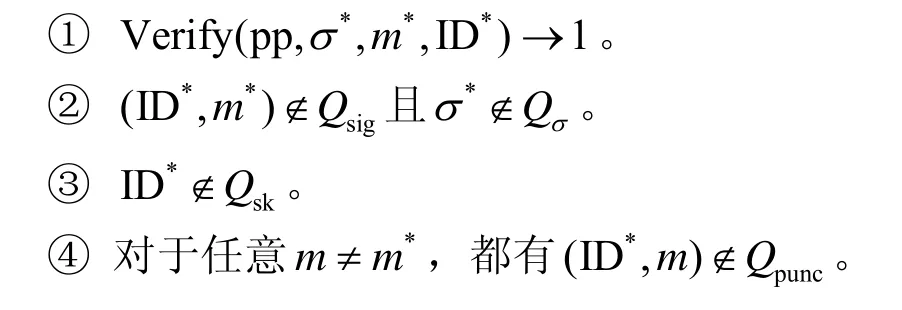
定義4IBPS 的存在不可偽造性。對任意一個針對IBPS方案的概率多項式時間敵手A，若其贏得上述安全游戲的概率是λ的一個可忽略函數，則稱該IBPS 方案滿足存在不可偽造性。

本文考慮一種較弱的存在不可偽造性，即選擇性存在不可偽造性，要求敵手A 在開始安全性游戲之前就將挑戰消息m*提交給挑戰者C。

5 方案具體構造

基于Paterson 等[3]的IBS 方案，本節給出一個具體的IBPS 方案構造，其核心在于如何實現用戶密鑰的穿刺操作。為此，本文借鑒Derler 等[23]提出的密鑰穿刺機制，利用布隆過濾器來管理用戶私鑰和簽名消息。具體而言，在生成用戶私鑰時，先初始化一個布隆過濾器(H,T)←BFGen(?,k)，然后對于T的每一個位置i∈[ ? ]，生成一個相應的私鑰構件ski；在對消息m進行簽名時，首先利用H將其映射到T的k個位置，從中選取一個滿足T[i′] ≠ 1的位置i′，然后利用相應的用戶私鑰構件進行簽名；在完成對m的簽名之后，將m添加到布隆過濾器中并更新其狀態BFUpdate(H,T,m)→T′，同時，在所有滿足T′[i]=1的位置，將相應的用戶私鑰構件設置為ski←⊥。可以看出，通過上述密鑰穿刺過程，用戶私鑰不能對已簽名過的消息進行再次簽名。具體構造的IBPS 方案由以下5 個算法組成。

Setup(λ)。給定系統安全參數λ之后，系統建立算法首先生成雙線性群 (G,GT,g,p,e)；然后，分別定義用戶身份標識空間ID={0,1}γ和簽名消息空間M={0,1}η，選擇 2 個 Hash 函數H:{0,1}*→{0,1}γ和H′:{0,1}*→{0,1}η，以及另外一個 Hash 函數H～ :N →G ；選擇隨機群元素g2,u0,vo∈G，以及2 個隨機向量u=(u1,… ,uγ)∈Gγ和v=(v1,…,vη)∈Gη；最后，選擇一個隨機整數α∈Zp，計算g1=gα，并令系統主密鑰為系統公開參數為pp={(G,GT,g,p,e),

Extract(pp,msk,ID)。給定系統公開參數pp、系統主密鑰msk 和用戶身份ID∈{0,1}*，私鑰提取算法首先將ID 映射到系統定義的身份標識空間，即令θ=H(ID)=(θ1,…,θγ) ∈{0,1}γ；然后，初始化一個布隆過濾器(H,T)←BFGen(?,k)，其中T=0?；選擇隨機整數r1,r2∈Zp，對任意整數i∈[? ]，按如下方式計算私鑰構件ski。

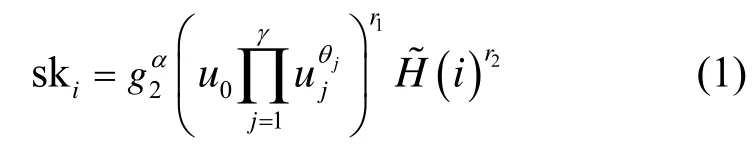
最后，按照如下結構輸出用戶私鑰。

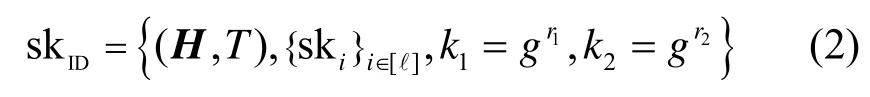
Punc(pp,skID,m)。給定系統公開參數pp、用戶的當前私鑰和一個消息m∈{0,1}*，令ω=H′(m)=(ω1,…,ωη)∈{0,1}η；然后，將消息m添加到布隆過濾器的集合中，并對其狀態進行更新，即令T′←BFUpdate(H,T,m)；對任意i∈［ ? ］，按照如下方式對相應的私鑰構件進行更新。

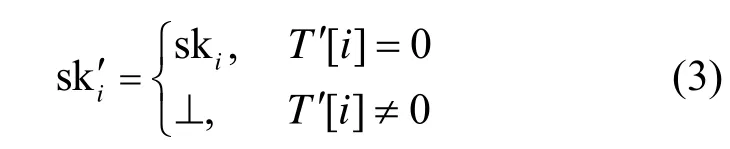
Sign(pp,skID,m) 。給定公開參數pp、用戶當前私鑰和待簽名消息m，若BFCheck(H,T,m)→1，則輸出錯誤符號⊥，否則，存在一個指標i*∈{i1,… ,ik}使其中i j=H j(m)(j∈ [k])；令ω=H′(m)=(ω1,…,ωη)，選取隨機指數rm∈Zp，計算

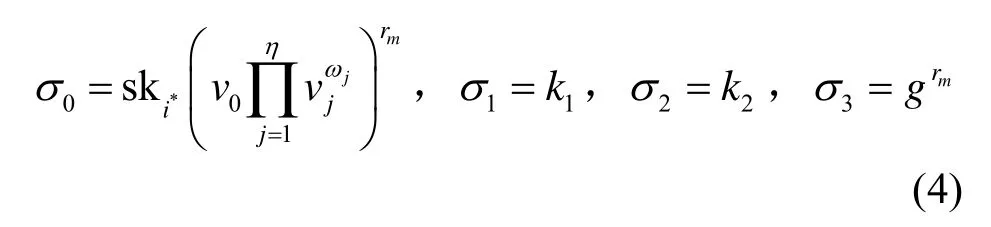
最后，返回簽名σ={i*,σ o,σ1,σ2,σ3}。

Verify(pp,σ,m,ID)。給定公開參數pp、簽名σ={i*,σ o,σ1,σ2,σ3}、消息m和用戶身份ID，首先令θ=H(ID)=(θ1,…,θγ)和ω=H′(m)=(ω1,…,ωη)；然后，驗證下述等式是否成立。

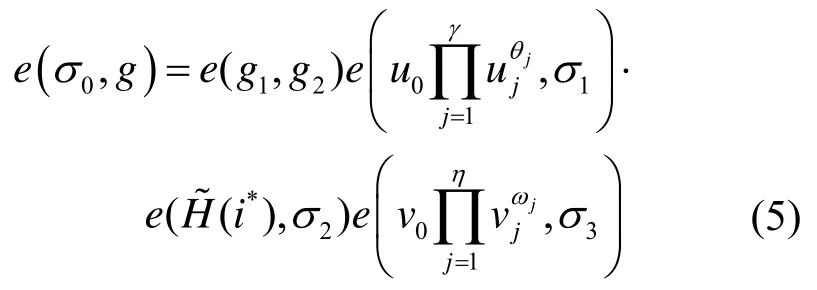
若等式成立，則說明σ是一個關于ID 和m的有效簽名，輸出1；否則輸出0。

方案正確性依據私鑰生成算法可知，私鑰構件sk*i的值為將其代入式(5)可得

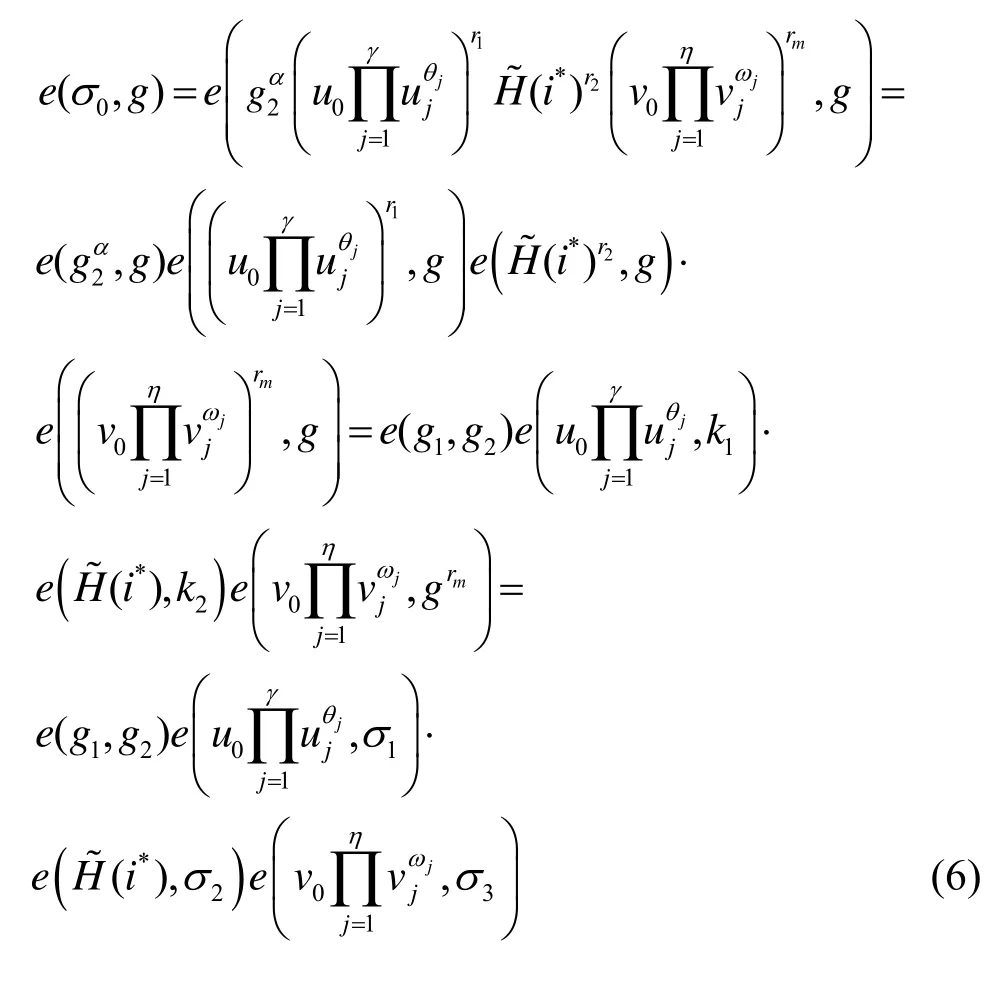
6 安全性證明及性能分析

6.1 安全性證明

定理1IBPS 方案安全性。對于依據安全參數λ生成的雙線性群 (G,GT,g,p,e)，若CDH 假設在群G 上成立，則所構造的IBPS 方案在隨機預言模型下滿足選擇性的存在不可偽造性。具體地，有

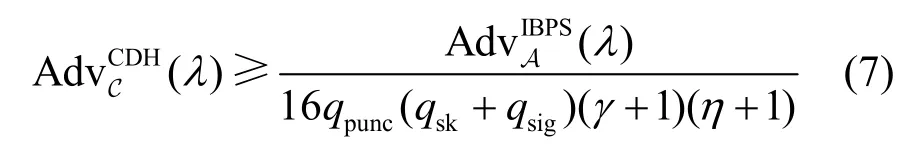
其中，qpunc是私鑰穿刺詢問次數，qsk是私鑰提取詢問次數，qsig是簽名詢問次數。

證明為證明定理1，主要采用Waters[16]提出的證明技巧，同時以隨機預言機的方式模擬Hash函數對其進行擴展。下面，給出挑戰者C 模擬安全性游戲各個階段的細節。

系統建立階段在初始階段，挑戰者C 收到一個雙線性群 (G,GT,g,p,e)，以及群G 上CDH 問題的實例(g a,gb)，其中a和b是選自中的隨機整數，C 的目標是計算出gab。此外，敵手A 需在安全性游戲開始之前提交挑戰消息m*。

在上述定義的基礎上，按如下方式設置所構造IBPS 方案的系統公開參數

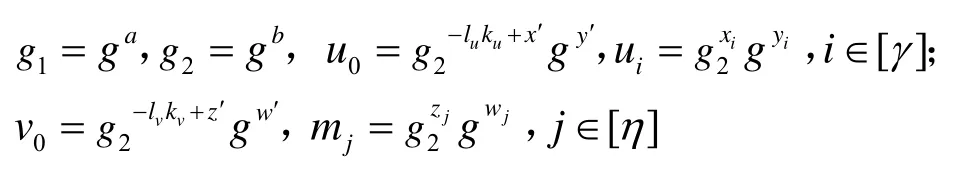
最后，C 初始化4 個空集Qsk←?、Qsig←?、Qσ←?和Qpunc←?，并將按照上述方式生成的系統公開參數發送給攻擊者A，同時還向其提供Hash 函數的查詢服務。

詢問階段在該階段，A 可以自適應地進行私鑰提取查詢、簽名查詢和私鑰穿刺查詢，這3 種詢問同時還涉及Hash 函數H,H′,的詢問。對于H和H′，挑戰者將它們模擬成一般的抗碰撞Hash函數。對于Hash 函數，挑戰者C 按照如下方式進行模擬：對任意i∈[ ? ]，選擇一個隨機整數ti∈Zp，若有i∈{H j(m*):j∈[k]}，則直接令否則令下面給出C 響應3 種查詢的方式。

1) 私鑰提取詢問。給定一個用戶身份ID，C 先令H(ID)=(θ1,…,θγ)，此時H被模擬成一個一般的抗碰撞Hash 函數。進一步，若有F(ID)=0 modp，則C 終止模擬，否則C 選擇隨機整數令然后，C 計算ID 所對應的私鑰構件ski

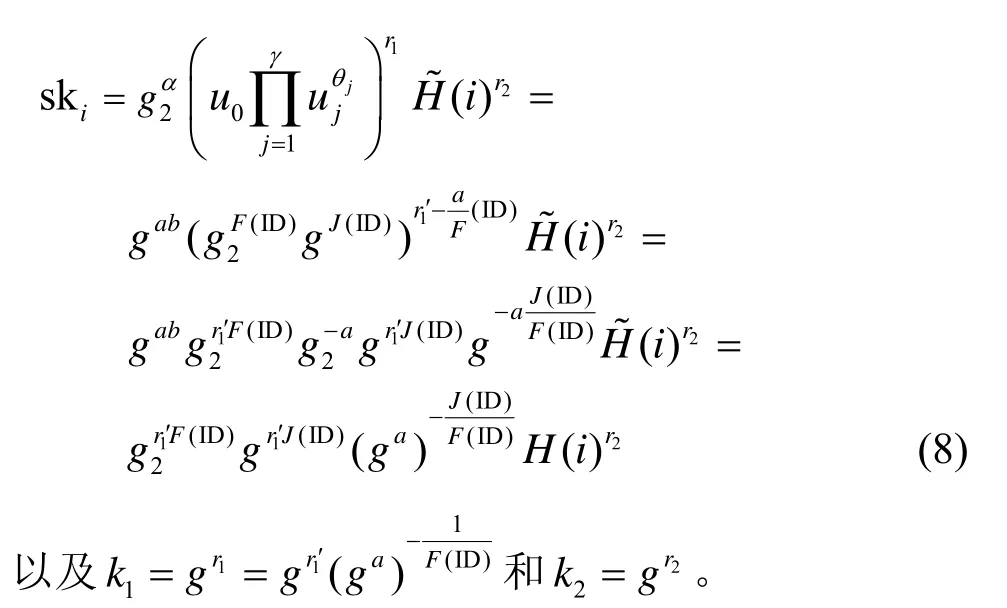
從式(8)中可以看出，盡管C 不知道系統主密鑰，但上述私鑰構件對其都是可計算的，并且與按照真實的私鑰提取算法所產生的私鑰是同分布的。最后，C 將ID 的私鑰發送給敵手A，同時更新集合

2) 簽名詢問。給定用戶身份ID 和待簽名消息m，挑戰者C 首先將它們映射到相應的二進制字符串，即此時若有則C 通過調用私鑰提取詢問先生成相應的用戶私鑰skID，然后直接利用IBPS方案的簽名算法即可生成關于ID 和m的正確簽名，并返回給敵手A。另一方面，若F(ID)=0 modp且K(m)=0 modp，則C 終止安全性游戲，否則C 選擇隨機整數并令，然后按照下述方式生成簽名

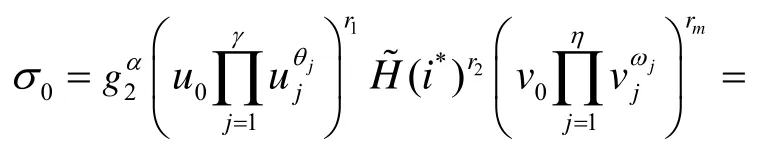
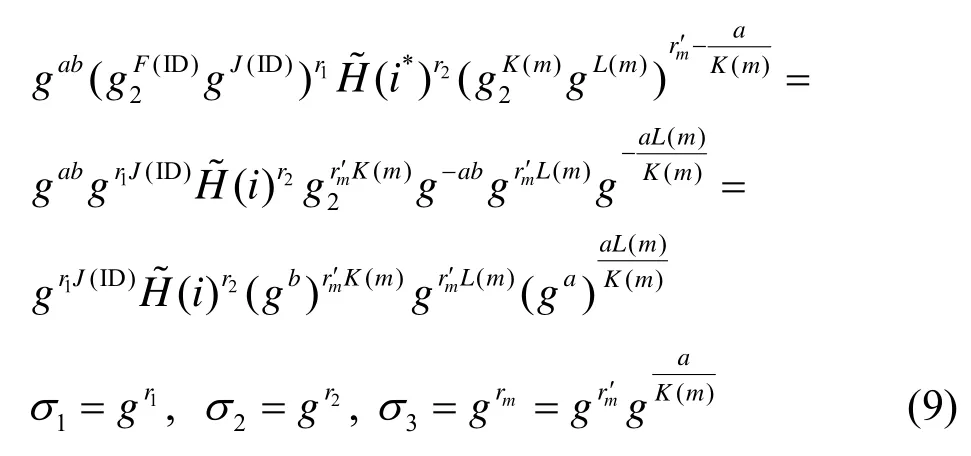
可以看出，上述簽名構件對C 都是可計算的，且與IBPS 方案中的簽名算法所產生的簽名同分布。最后，C 將關于ID 和m的簽名σ={i*,σ o,σ1,σ2,σ3}返回給敵手A，同時更新集合Qsig←Qsig∪{(ID,m)}和Qσ←Qσ∪{σ}。

3) 私鑰穿刺詢問。在響應該詢問之前，挑戰者C 先猜測敵手A 的第j次該詢問是關于挑戰身份ID*的查詢，若猜測失敗，則終止安全性游戲。對于關于其他用戶身份的私鑰穿刺詢問，C 先調用私鑰提取詢問得到相應的用戶私鑰，然后利用IBPS方案的私鑰穿刺算法即可得到穿刺后的私鑰，并將其返回給敵手A。特別地，對于A 的第j次詢問，由安全模型中對敵手的約束可知，此時A 提供的就是挑戰身份ID*和挑戰消息m*。為生成穿刺后的用戶私鑰，C 選擇隨機整數對任意i∈[ ? ]，若，則令ski←⊥，否則按照下述方式計算ski

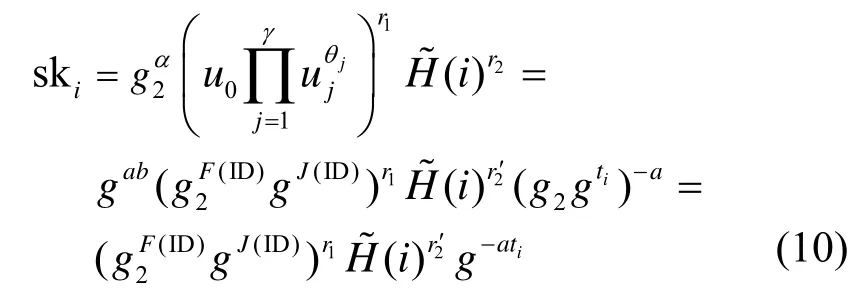
偽造階段敵手A 結束詢問階段之后，輸出一個關于(m*,ID*)的簽名同時滿足下述條件。

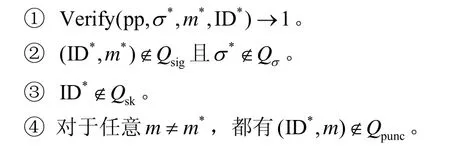
此時，若F(ID*) ≠0 modp或K(m*) ≠0 modp，則挑戰者C 直接終止安全性游戲。最終，若挑戰者C沒有終止安全性優勢，則可按照下述方式計算出gab。

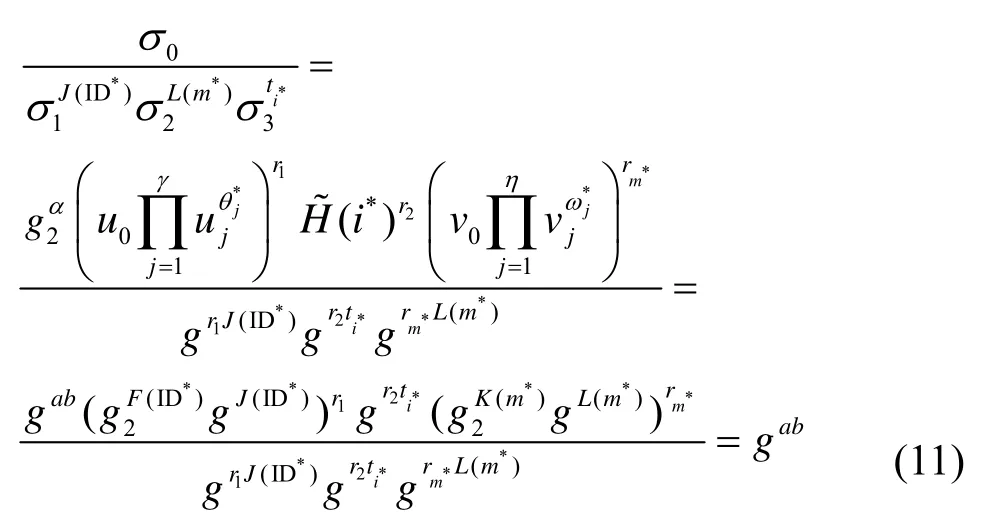
從而解決了給定的CDH 問題實例。

概率分析挑戰者C 能計算出abg的前提是不終止安全性游戲，而由Waters[16]的“artificial abort”分析技術可得，C 不終止安全性游戲的概率為

6.2 性能分析

表1 給出了本文所提IBPS 方案與其他相關簽名方案在計算開銷和存儲開銷方面的比較。在比較過程中，用e 表示一次模指數運算，p 表示一次雙線性對運算，γ表示用戶身份的長度，η表示簽名消息的長度，? 表示布隆過濾器的數組長度，N表示時間周期總數，G 表示一個群元素。在比較過程中忽略運算時間非常小的Hash 運算。

表1 相關簽名方案的計算/存儲開銷比較

從表1 中可以看出，相比于Paterson 等[3]的IBS 方案，本文所提IBPS 方案在私鑰提取算法上具有較大的計算開銷，這主要是由于為了實現細粒度的前向安全性，額外地為布隆過濾器所對應的二進制序列的每一個位置上都生成了一個私鑰構件。另一方面，相比于Yu 等[14]的前向安全IBS方案，本文所提IBPS 方案的密鑰穿刺/更新開銷主要是Hash 運算和刪除運算，幾乎可以忽略，而Yu 等[14]的前向安全IBS 方案的密鑰更新開銷與總的時間周期數目成對數關系。此外，在存儲開銷方面，本文所提IBPS 方案的公開參數規模與Paterson 等[3]的IBS 方案相當，而Yu 等[14]的前向安全IBS 方案具有更大的公開參數規模。在簽名長度方面，本文所提方案與Yu 等[14]的前向安全IBS 方案相同，均略高于Paterson 等[3]的IBS 方案。特別地，Yu 等[14]的前向安全IBS 方案的私鑰規模與總的時間周期總數的對數成平方關系，具有較高的存儲開銷。

表2 給出了相關簽名方案在安全性質方面的比較。從表2 可以看出，只有本文所提方案具有細粒度的前向安全性，但其安全性卻是在隨機預言模型下證明的，而非標準模型。此外，在安全性假設方面，Yu 等[14]方案的安全性基于一個更強的q-型Diffie-Hellman 指數困難性問題假設。

表2 相關簽名方案的安全性質比較

6.3 仿真實驗

為驗證所構造IBPS 方案的實際性能，將其在Charm[28]框架下進行了實現，并測試了各個算法的實際運行時間。所有的測試實驗均是在具有16 GB內存和i7-1160G7@1.20GHz CPU 的PC 上進行的。

在仿真實驗中，布隆過濾器中的集合規模設置為n=220，即允許用戶在一年中每天向其中添加 212個元素，同時布隆過濾器的假陽性概率設置為δ=10-3，表示布隆過濾器的字符串長度為?=1.7 ×107，Hash 函數個數為k=10。在一般的前向安全IBS 方案中，設定總的時間周期數為N=219，即允許用戶在一年的時間里每隔一分鐘更新一次私鑰。所采用的 Hash 函數均為SHA-256，橢圓曲線為Charm 提供的SS512 曲線和SS1024 曲線。

圖1 給出了相關基于身份簽名方案中各個算法運行時間對比。從圖1 可以看出，本文所提IBPS方案的私鑰抽取算法的運行時間要遠高于其他2 個方案，但該算法一般都是離線運行且執行一次，故在實際中不影響系統性能。另一方面，本文所提IBPS方案的私鑰更新效率非常高。具體地，在SS512 曲線下，私鑰穿刺算法的運行時間僅有2.32 s，而Yu等[14]方案中算法的運行時間則接近350 s，比本文所提IBPS 方案高了近150 倍。

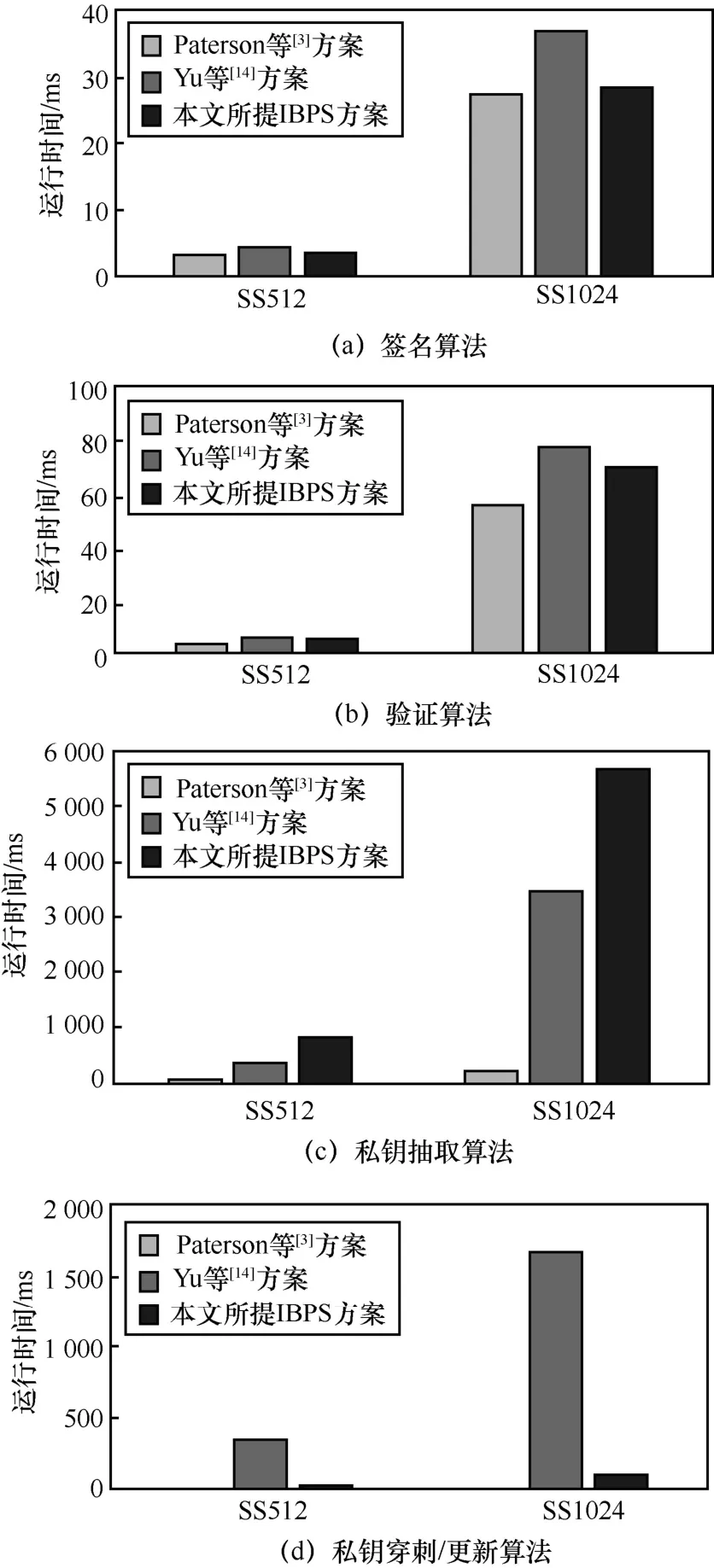
圖1 相關基于身份簽名方案中各個算法運行時間對比

圖2 給出了相關IBS 方案的存儲開銷。從圖2可以看出，由于產生了私鑰構件的多個備份，本文所提IBPS 方案具有較大的私鑰規模。

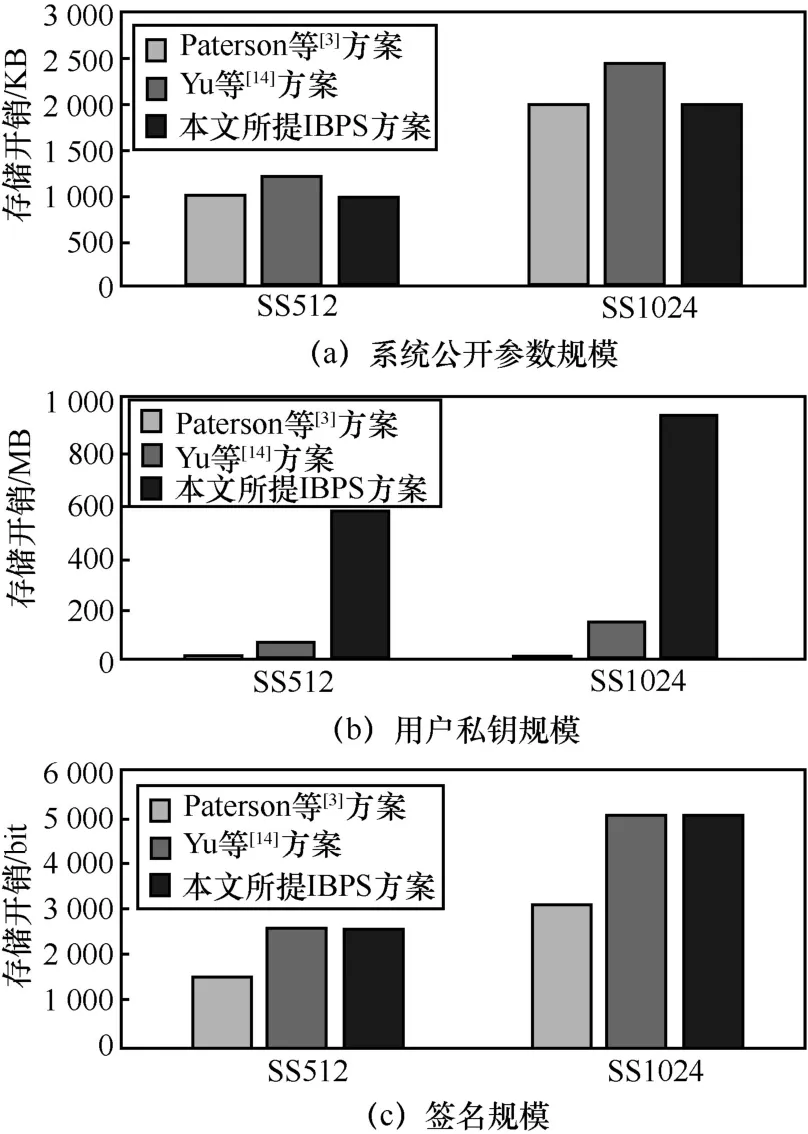
圖2 相關IBS 方案的存儲開銷

6.4 方案應用

本文所提IBPS 方案可以在任何部署過IBS 的場景中使用，以增強用戶私鑰的前向安全性。下面以IBPS 在監控系統的應用為例，如圖3 所示。目前的物聯網技術和無線通信技術支持部署大規模的監控系統，物聯網設備、智能手機、無線攝像頭、無線相機等向云服務器提供視頻和圖像，即向監控系統提供監控數據。一個安全可靠的監控系統，應該做到設備提供的視頻和圖像確保是真實的，不是被修改或偽造的；設備需要諸如公鑰證書等憑證來提供視頻和圖像的真實性；任何攻擊或私鑰泄露不會破壞所有以前的監控數據，即應當保證監控數據的前向安全。

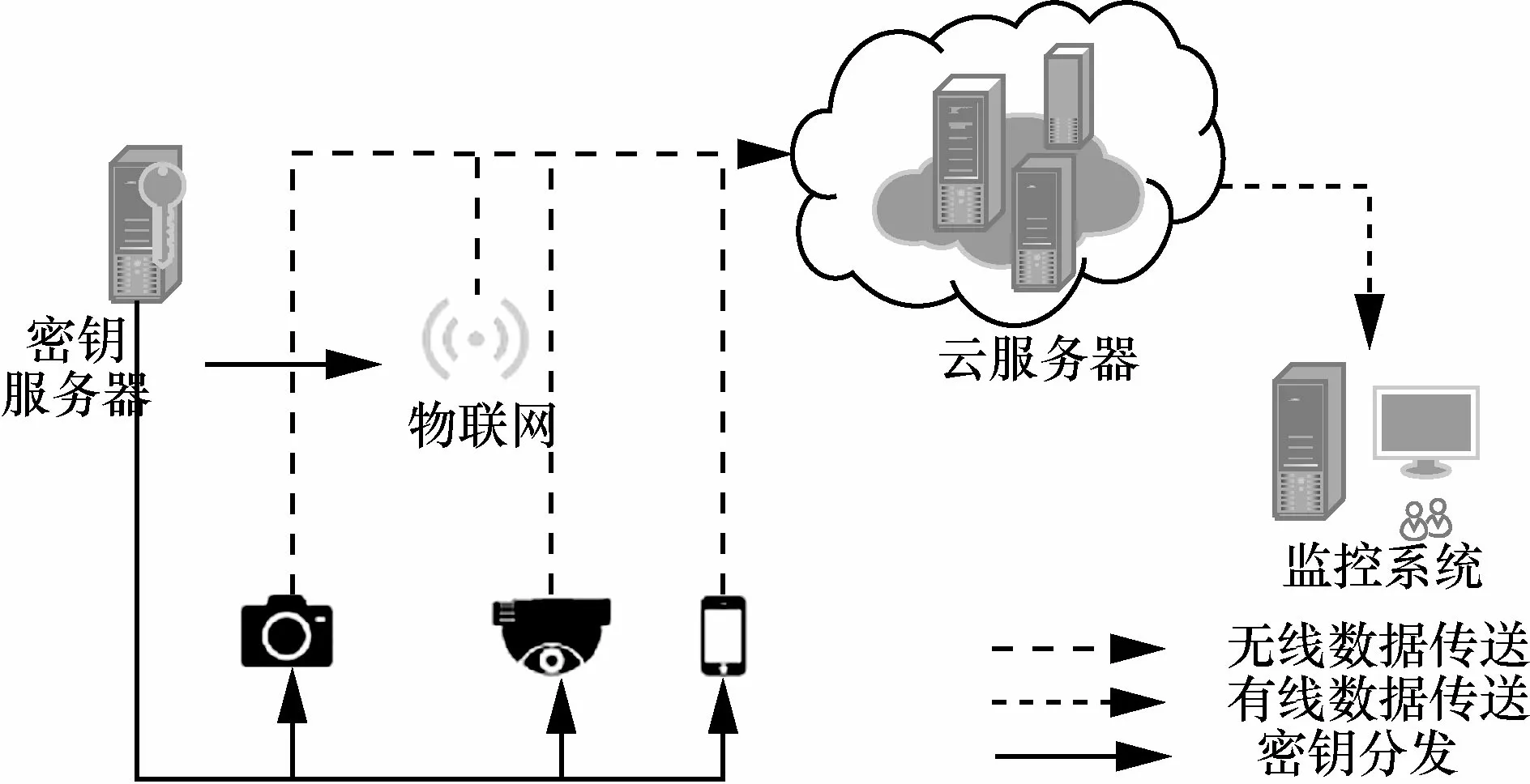
圖3 IBPS 在監控系統的應用

本文所提IBPS 方案為解決上述實際問題提供了可靠對策。圖3 中的每個設備將其身份標識注冊到云服務器，密鑰服務器負責為每個設備分發與其身份標識對應的私鑰，同時，把自己的公鑰發送給云服務器。當設備發送數據時，先對數據簽名，然后把簽名和數據一起發送，而云服務器只接受其簽名有效的數據。這樣，一方面保證了數據來源的真實性，另一方面云服務器利用密鑰服務器的公鑰驗證接收的數據，而設備不需要攜帶證書。每發送完一次數據，該設備都進行密鑰穿刺操作，完成私鑰的更新。這保證了任何設備在私鑰泄露的情況下，該設備所有以前的簽名仍然有效。

7 結束語

本文針對已有的前向安全的基于身份簽名方案的靈活性不強、私鑰更新效率較低的問題，通過引入可穿刺公鑰加密思想，提出了基于身份的可穿刺簽名方案。基于Paterson 等[3]的基于身份簽名方案，利用布隆過濾器構造了一個具體的基于身份的可穿刺簽名方案，以較高的存儲開銷為代價，實現了簽名的細粒度前向安全性和用戶私鑰的高效更新。安全性證明表明，本文所提IBPS 方案在隨機預言模型下滿足存在不可偽造性。理論分析和實驗結果表明，本文所提IBPS 方案在安全性和效率方面具有優勢，更適合在實際應用中部署。