一類圓邊界中求勻強電場的方法與技巧
鄧 艾 張海深
(湖北省武漢市吳家山中學,湖北 武漢 430040)
1 引言
高中階段在學習靜電場章節時,經常會遇到已知特殊幾個位置的電勢求勻強電場的大小與方向的題.求解勻強電場的過程滲透學生對U=E d公式的理解與應用,式中d是指沿電場線方向的距離,U是指電勢差.由此可見計算距離d過程往往伴隨位置關系的幾何分析.電勢差的分析蘊含對電場基本性質的認識,在有些情況下電勢差的計算往往還伴隨電勢能與其他能量轉化.這類問題一方面考查學生對電場本質的認識,需建構準確的完整的自然圖景;另一方面考查學生在處理場類問題時應建構正確的能量觀與相互作用觀,同時應具備一定的模型建構能力,科學推理能力.下面我們以一些典型例題詳細說明具體的解題思路與技巧.
2 電勢與電場強度
2.1 二維平面內電場強度求解
例1.如圖1所示,在平面直角坐標系中,有方向平行于坐標平面的勻強電場,其中坐標原點O處的電勢為0V,點A處的電勢為6V,點B處的電勢為3V,求勻強電場大小和方向.

圖1
方法1:等勢點法.取O A中點C,則C點電勢為3V,則B C作為等勢線,電場線垂直于B C線段,根據公式可求出場強E=200V/m;方向與x軸正方向成120°斜向左下方.
方法2:矢量分解法.x方向電場Ex=100V/m,y方向電場合成的勻強電場滿足方向同上.
2.2 三維平面內電場強度求解
例2.如圖2所示,空間中存在著勻強電場,長方體ABCD-A1B1C1D1中ADD1A1是邊長為1m的正方形,棱AB長2m,E、F為棱AB、CD的中點,E1、F1為棱A1B1、C1D1的中點.已知電勢φA1=0,φA=2 V,φE=4V,φB=6V,φC=8V.求勻強電場大小和方向.

圖2
通過以上2個例題介紹了求解勻強電場的基本方法.可以發現:在二維平面模型中,利用等勢點法與矢量分解的方法都可以很好地解決電場強度的求解.相比之下等勢點法更快,這種方法也更容易被學生理解.但是三維立體空間中,等勢點法在計算距離d時對學生的空間想象能力和計算能力提出較高的要求.因此當勻強電場在三維空間內分布但是方向不明的情況下,利用矢量分解的思想可以將三維空間問題轉化為3個相互正交方向上的一維問題的處理,有效降低思維的難度,因而這種情況下矢量分解的思想比等勢點法更有效.
2.3 二維圓平面內電場強度求解
例3.如圖3所示,a、b、c、d是圓O上的4點,AB=5c m,c d=8c m,∠b a c=60°,勻強電場的方向與圓所在平面平行,已知a、b、d3點電勢分別為φa=46 V、φb=21V、φd=10V,求該勻強電場.

圖3
方法1:求解勻強電場常見的基本思路是尋找等電勢點,再利用公式U=Ed進行計算.本題也可以充分利用圓平面內利用現有邊長關系與電勢數值,構建出等電勢點.
線段a d上總的電勢差為36V,按照比例進行六等份,每等份的電勢差為6V,因此圖4中φe=16V;線段AB上總的電勢差為25V,按照比例進行5等份,每等份的電勢差為5 V,因此圖2中φf=16V;可以發現e,f兩點電勢相等.線段a e=5c m,線段a f=6c m,∠d a c=53°,∠c a b=60°,可以發現a e×cos 53°=a f×cos 60°,因此e f⊥a e;電場的方向沿a c方向;電場強度大小滿足E=代入數據得E=10V/c m.
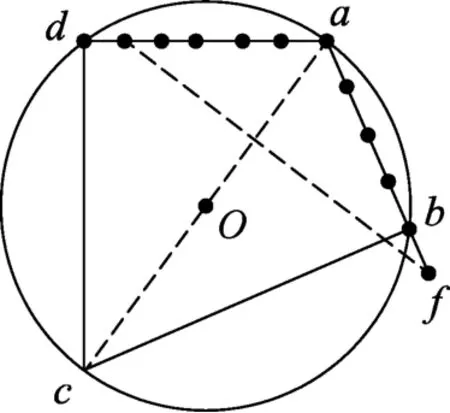
圖4
方法2:假設c點的電勢為φ,以da,dc為基底表示出的電場強度滿足以ba,bc為基底表示出的電場強度滿足E=-5m+兩種情況下場強E的大小相等,故62+解得φ=-54V,E=10V/c m,方向沿a c方向.
方法3:根據勻強電場在圓平面內的特點,b的等勢點一定在a為圓心,以AB長度為半徑的圓上.據此我們畫出這個圓,與題設給定圓的交點為e,如圖5所示.同時結合φa=46V、φd=10V,可判斷圓弧AB上一定存在電勢為21V的點,即兩圓的交點e.進一步分析可知:場強沿ac方向.

圖5
總結:例3運用3種方法求解電場強度.其中方法1解題的策略是突破圓的限制,整合邊長和電勢的數量關系,創設等勢點尋找電場強度;方法2是利用電場矢量沿不同方向進行分解的思想,直接建立關于c點電勢的方程;方法3基于平面內的勻強電場中,任意兩個等勢點應滿足的特點進行動態分析.
以上3道例題中,基于線,面,體3種模型和具體實例詳細闡述了求解勻強電場的基本方法與特殊技巧.這類題目解題的關鍵在于:分析問題情境,充分挖掘題目中幾何位置關系和特殊點的電勢值,需要學生利用數學知識解決物理問題.以例3中創設的圓邊界為例,電場強度的求解既可以突破圓邊界的限制,構建等勢點;也可以靈活利用圓形邊界上以直徑兩端為頂點的三角形的特殊性,充分利用隱含的直角坐標軸建立相關方程;也可以從平面內勻強電場的特殊性進行動態分析與處理.
在上述例題中,主要基本電勢差與電場強度的基本概念與公式的運用進行詳細的探討與分析.這些問題主要考查利用公式與具體的問題情境進行科學推理能力與模型建構能力.下文我們進一步以圓形邊界為依托,分析粒子在電場力作用下根據能量轉化信息求電場強度的基本思想與方法.
3 電勢能與電場強度
3.1 復合場與等勢線
例4.如圖6所示,勻強電場中有一半徑為R的圓形區域,勻強電場方向平行于圓所在平面(圖中未畫出),圓形區域處在豎直平面內,圓周上有8個點等間距排列.一重力不可忽略的帶正電小球從A點以相同的初動能在該平面內拋出,拋出方向不同時,小球會經過圓周上不同的點,在這些所有的點中,到達D點時小球的動能最大.已知小球質量為m,電荷量為q,重力加速度為g,求電場強度應滿足的條件.

圖6
在勻強電場中,如圖7所示,若勻強電場的方向水平向右,則與電場垂直的線a、b、c稱為等勢線.若帶電粒子在僅受電場力作用下運動,則粒子能量在相互轉化過程中保持動能與電勢能之和不變,意即粒子運動至同一等勢線上的動能均相同.

圖7
本題基本思想是將恒定的重力場與恒定的電場等效為一個復合場,復合場具有一個確定的方向,與復合場垂直的方向我們仍然可以定義為等勢線.粒子在復合場中運動,動能與勢能相互轉化.小球運動到D點動能最大,說明D點是圓平面上唯一一個勢能最小的位置,結合圓的幾何性質可知:等勢線與圓在D點的切線重合,復合場中等效場強的方向:沿過D點的半徑O D方向.如圖8所示,作出與O D垂直一系列等勢線,等勢線L2與圓有兩個交點,說明粒子從圓上這兩個點出射時勢能相同,動能相同;從功能關系的角度分析,沿場強方向的位移一樣,合力做功一樣,動能一樣.

圖8
解析:電場與重力場的合場強方向沿O D方向,因重力與電場的大小不確定,因此勻強電場的大小和方向不確定.但是根據矢量合成遵從的平行四邊形法則,可以找出最小的勻強電場的大小與方向.
針對部分學生可能出現的思維誤區:既然從A點出發,到D點動能最大,為什么復合場中合力方向不能沿AD方向?我們據此作出相關的幾何圖.假設復合場沿AD方向,則與AD垂直的D E方向為等勢線,如圖中標出的L1,可以看到等勢線L1順著圓往右下側移動,如圖9中L2,顯然L2勢能更小,出射出去的動能更大.從等勢線的變化趨勢來看,最低的等勢線應與圓相切.出現上述思維誤區的原因是:對有一定初始速度的粒子在復合場中做曲線運動時動力學過程和功能關系認識不全面.但是本題中如果改變初始條件即粒子從A點由靜止開始運動,則可以認為合力沿AD方向.

圖9
實際上將粒子運動與電場力、能量問題、圓邊界聯系的問題早在2020年全國Ⅰ卷的壓軸題中就曾經出現.我們以此為例再來體會一下在圓邊界中,創設不同的初始條件,從不同角度設置問題情境導致解決問題的差異性與相似性.
3.2 回顧高考題與改編高考題
例5.在一柱形區域內有勻強電場,柱的橫截面積是以O為圓心,半徑為R的圓,AB為圓的直徑,如圖10所示.質量為m,電荷量為q(q>0)的帶電粒子在紙面內自A點先后以不同的速度進入電場,速度方向與電場的方向垂直.已知剛進入電場時速度為0的粒子,自圓周上的C點以速率v0穿出電場,A C與AB的夾角θ=60°.運動中粒子僅受電場力作用.

圖10
(1)求電場強度的大小;
(2)為使粒子穿過電場后的動能增量最大,該粒子進入電場時的速度應為多大?
第(2)問解析:根據第(1)問勻強電場沿A C方向,與A C垂直的方向即B C方向等勢線,作出一系列平行的線段即為等勢線,可以發現最低等勢線處于與圓相切的D點.根據能量轉化與守恒,粒子到達D點的速度最大.
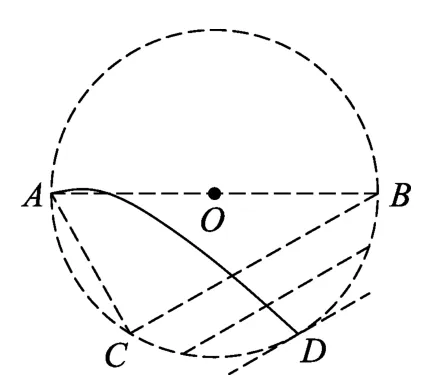
圖11
總結:在上述例4與例5中我們著重從等勢線的角度,快速分析如何尋找粒子從圓邊界中射出時最大動能點位置.這類問題往往涉及大量粒子源,給定初始動能,但是具體速度方向不確定,或者大量粒子源的速度方向確定,但是速度大小不確定的情況下,分析動能與電勢能轉化過程中的最值問題.
整合以上問題,我們可以對上述高考題進行改編,從不同角度與層面強化對問題的理解與認識.
試題改編:假設粒子進入電場時速度方向在圓平面內沿各個方向,但是粒子速度大小確定.
(1)若所有粒子能射出圓邊界,求入射粒子速度應滿足條件.
(2)若粒子射出圓邊界時與初動能相同,求滿足條件的入射粒子最小動能多大?
根據上述作出的等勢線,可知粒子出圓邊界的速度不變,則粒子運動的合位移一定沿過A點的等勢線,如圖12.根據運動的分解粒子速度平方滿足根據數學中不等式知識:當且僅當即時具有最小動能

圖12
3 結束語
圍繞靜電場中勻強電場的求解,我們從基本方法的梳理到特殊技巧與方法的運用.結合具體問題的探討,以圓邊界為例,從基本公式的運用到與電場有關能量問題的分析,較為系統地總結相關的解題技巧.這些例題能進一步促進學生形成電場的物質觀、運動觀、相互作用觀和能量觀.不同問題情境的創設能有效提升學生模型建構、科學推理、綜合分析、質疑創新的科學思維.[1]

