基于GeoGebra軟件的回旋加速器工作原理分析
——以2021年江蘇省高考物理第15題為例

石 超 吳夢雷

（1.江蘇省邗江中學，江蘇 揚州 225009；2.江蘇省揚州中學，江蘇 揚州 225009）

2019年教育部考試中心頒布了《中國高考評價體系》，針對高考命題，提出了“一核四層四翼”的要求，其中“四翼”指高考命題須兼顧基礎性、綜合性、應用性和創(chuàng)新性.回旋加速器工作原理對物理概念、科學思維的要求都很高，非常適合作為學習探索情境來考查學生的學科核心素養(yǎng).江蘇高考自“08方案”起，一直將其作為考查的重點，僅以計算題形式呈現(xiàn)的考題就呈現(xiàn)了3次.2021年是江蘇進入新高考的元年，第15題作為壓軸題，再次考查了回旋加速器的工作原理，旨在突出理論知識與生產生活實際、現(xiàn)代高科技的緊密聯(lián)系，是一道體現(xiàn)應用性和創(chuàng)新性的高品質試題.此類試題對學生的科學思維能力要求極高，筆者借助GeoGebra軟件直觀呈現(xiàn)了回旋加速器中粒子的運動軌跡，化抽象為形象，有效突破思維障礙，加深了學生對回旋加速器原理的認識.下面與讀者一同分析這道質量很高的高考試題.

例題.（2021年江蘇省高考第15題）如題圖1所示，回旋加速器的圓形勻強磁場區(qū)域以O點為圓心，磁感應強度大小為B，加速電壓的大小為U、質量為m、電荷量為q的粒子從O附近飄入加速電場，多次加速后粒子經過P點繞O做圓周運動，半徑為R，粒子在電場中的加速時間可以忽略.為將粒子引出磁場，在P位置安裝一個“靜電偏轉器”，如題圖2所示，偏轉器的兩極板M和N厚度均勻，構成的圓弧形狹縫圓心為Q、圓心角為α，當M、N間加有電壓時，狹縫中產生電場強度大小為E的電場，使粒子恰能通過狹縫，粒子在再次被加速前射出磁場，不計M、N間的距離.求：

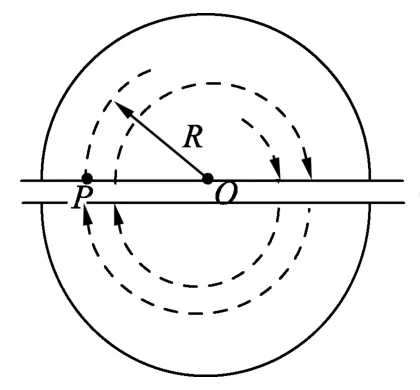
圖1

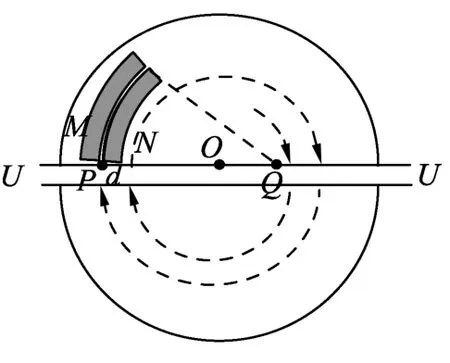
圖2

（1）粒子加速到P點所需要的時間t；

（2）極板N的最大厚度dm；

（3）磁場區(qū)域的最大半徑Rm.

解析：由題圖可知，帶電粒子在磁場中做順時針方向的勻速圓周運動，利用GeoGebra軟件作出粒子的軌跡，如圖3.

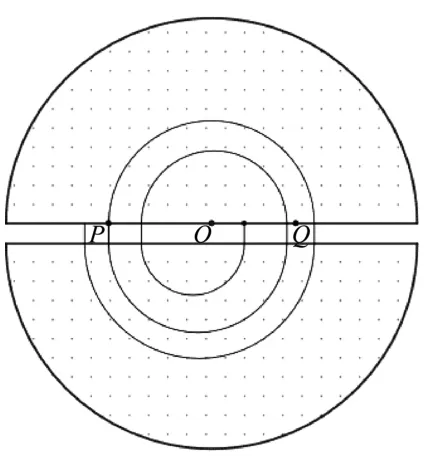
圖3

設粒子經過n次加速到達P位置，速度為vP，

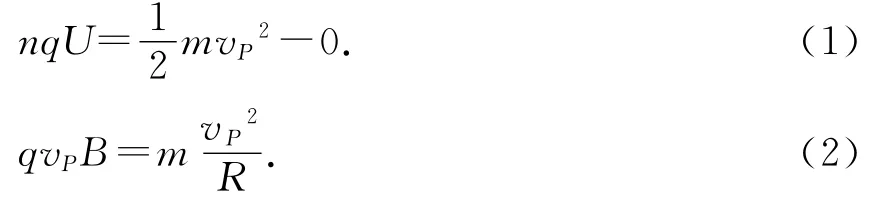
粒子加速到P點所需要的時間

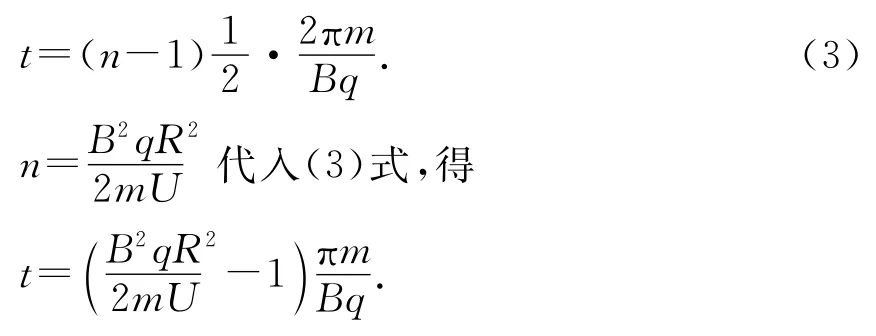
相較于后兩問，第（1）問較簡單，考生即使無法正確找到粒子出發(fā)點，但只要了解回旋加速器的工作原理，知道粒子的運動過程，畫出粗略的軌跡，就能正確作答.需要注意的是，粒子加速的次數(shù)容易出錯，應比半圓個數(shù)多1.

（2）設粒子經過n次加速后，半徑為rn，由（1）、（2）式，

粒子第n次經過D型盒邊界時，沿狹縫方向，距出發(fā)點的距離為

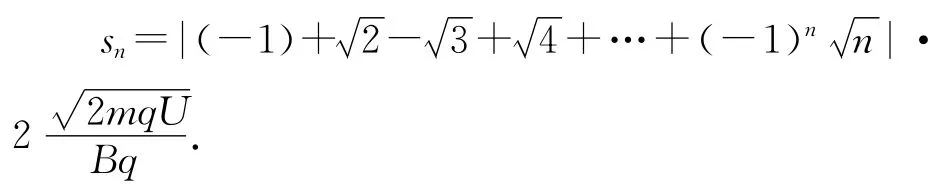
按圖3，n取奇數(shù)，粒子在出發(fā)點右側；n取偶數(shù)，粒子在出發(fā)點左側.每次經過加速，軌跡圓半徑均有一定程度放大，因此不難發(fā)現(xiàn)同側軌跡圓的圓心并不重合.如圖4所示，依據粒子運動規(guī)律，利用GeoGebra軟件的序列指令和映射指令可以作出粒子軌跡和圓心（圖4中靠得很近的點為相應軌跡圓的圓心）.依題意，在P位置安裝一個“靜電偏轉器”，粒子經過以O為圓心的P點，通過GeoGebra軟件改變板N的厚度，可作出圖5至圖7的動態(tài)變化過程.若極板N太厚，如圖7所示，板N的內側邊緣擋住軌跡Ⅰ，則粒子無法完成軌跡Ⅰ和軌跡Ⅱ而到達P點，所以極板N的最大厚度dm等于圖6中軌跡Ⅰ與軌跡Ⅲ的間距.因軌跡Ⅲ與軌跡Ⅰ的圓心不在同一點，所以dm≠而應該是

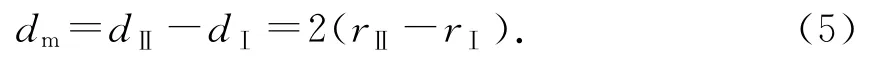
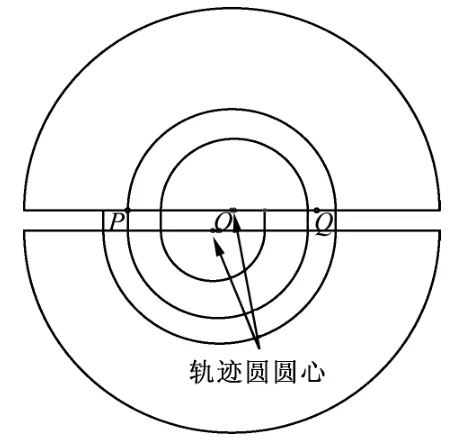
圖4

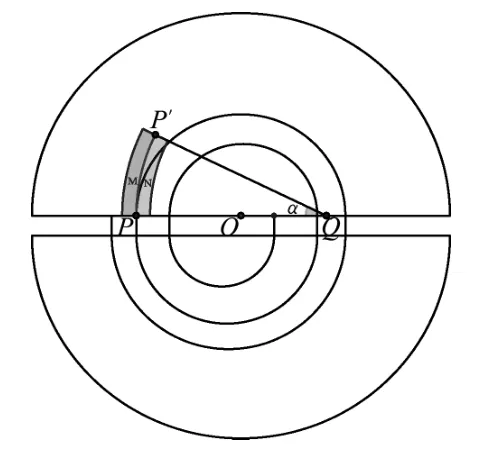
圖5

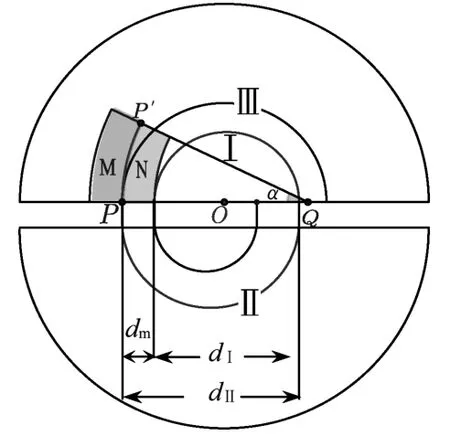
圖6

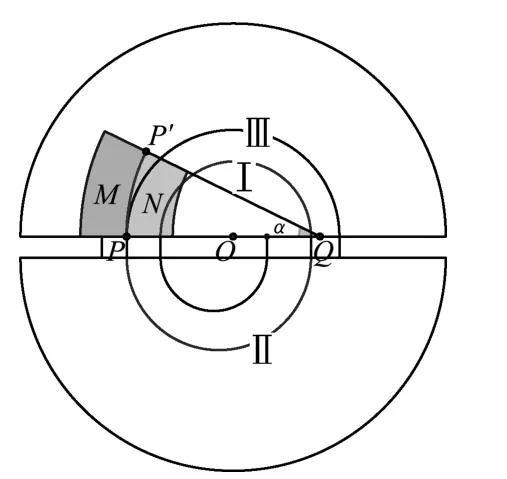
圖7

由（4）式知軌跡Ⅲ半徑

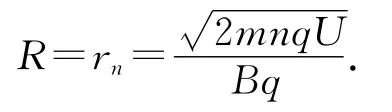
軌跡Ⅱ：

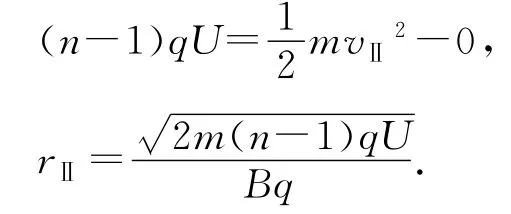
軌跡Ⅰ：

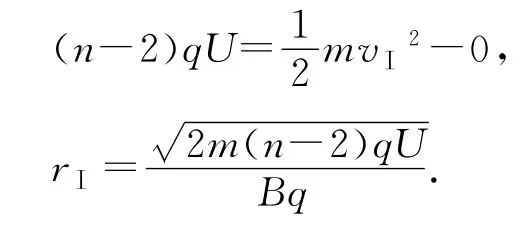
將rⅡ、rⅠ代入（5）式，得

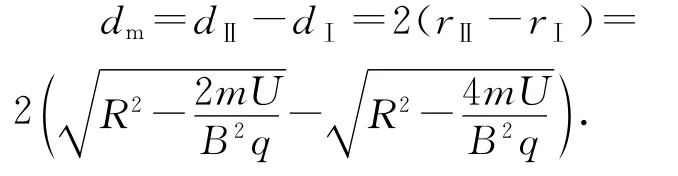
第（2）問，考生所犯的典型錯誤是認為dm=誤認為軌跡Ⅰ與軌跡Ⅲ具有相同的圓心.本問注重考查學生的思維能力和理論推導能力，有一定的難度.

（3）未安裝“靜電偏轉器”，粒子過P點：R=得

安裝“靜電偏轉器”后，粒子在P點速率并不能突變，圓心由O突變?yōu)镼，半徑增大，向心力減小，所以“靜電偏轉器”施加沿半徑向外的電場力，使粒子在洛倫茲力和電場力共同作用下沿“靜電偏轉器”的狹縫運動.電場力、洛倫茲力均與速度垂直，所以粒子做勻速圓周運動通過狹縫，設粒子繞Q點做勻速圓周運動的半徑為rQ，

粒子通過“靜電偏轉器”狹縫從P′點再次進入磁場以圓心為O′做半徑為R的勻速圓周運動，如圖8所示.若磁場半徑較大，粒子可運動至D型盒邊界而再次被加速，為避免這種情形，需減小磁場半徑至圖10中兩個半圓形虛線所示位置，使粒子在再次被加速前射出磁場.通過GeoGebra軟件改變磁場半徑，可作出圖8至圖10的動態(tài)變化過程（兩個半圓形虛線邊界即磁場邊界），由此可找出臨界條件：將粒子恰好能引出磁場，粒子軌跡與磁場邊界相切于G點.由幾何關系可知，此時O、O′、G三點共線.

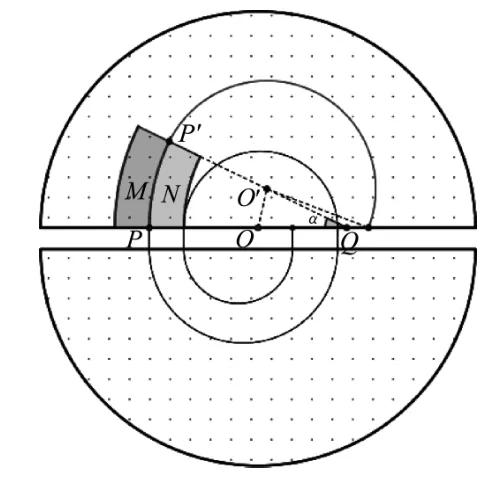
圖8

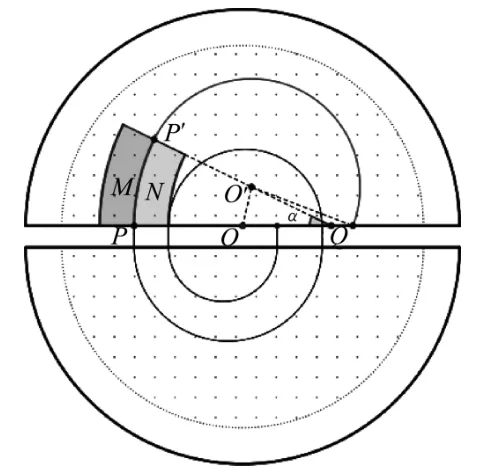
圖9

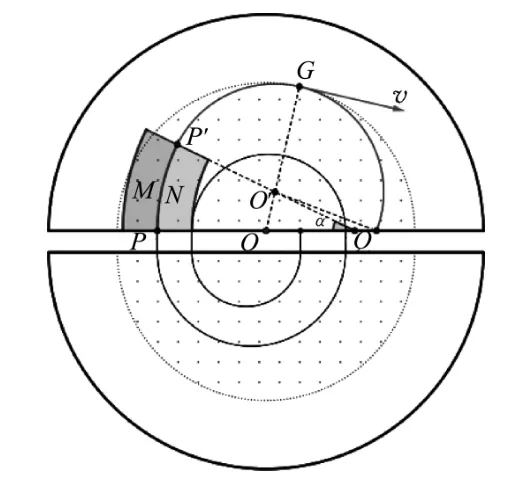
圖10

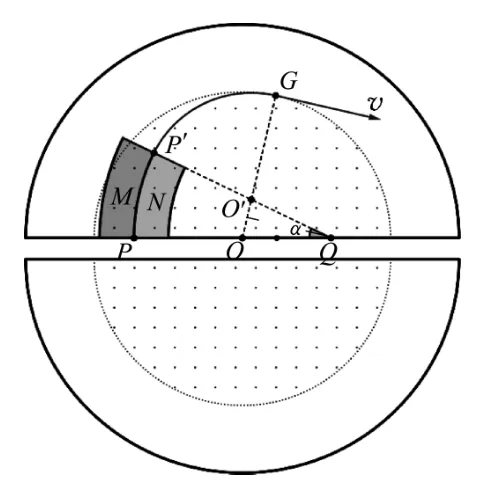
圖11

為方便計算，利用GeoGebra軟件隱藏粒子運動至P點前的軌跡，得到圖11.由圖11可清晰得出磁場區(qū)域的最大半徑

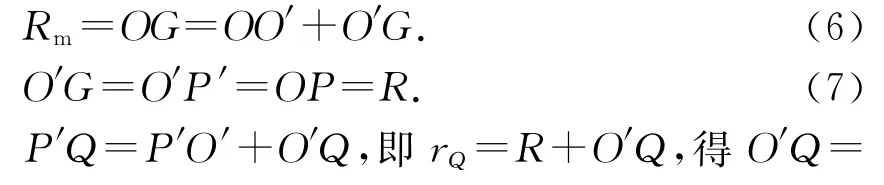
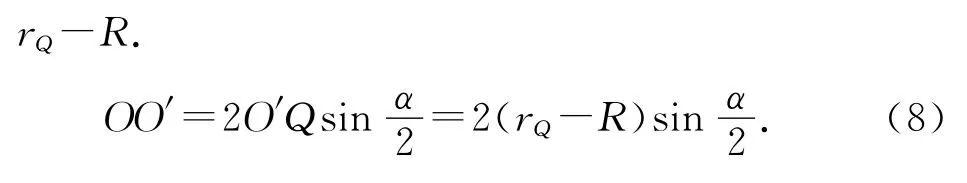
將（7）、（8）式代入（6）式得

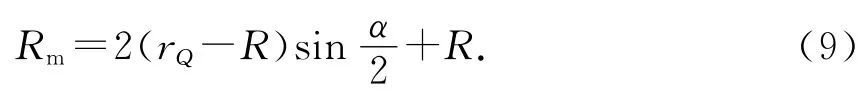
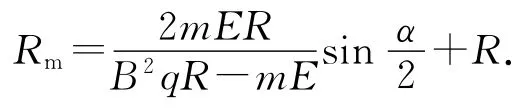
第（3）問通過巧妙地引入“靜電偏轉器”，重點考查了粒子在復合場中的勻速圓周運動、邊界磁場中勻速圓周運動的臨界問題等，有較強的綜合性，很好地體現(xiàn)科學思維和學科素養(yǎng).

小結：本題突出了“四翼”中的應用性和創(chuàng)新性，立足回旋加速器的工作原理，重點考查動能定理、帶電粒子在勻強磁場中運動規(guī)律.通過在粒子經過的P位置安裝一個“靜電偏轉器”，使粒子在再次加速前被射出磁場，構造了新的情境，著重考查學生的模型建構能力、推理論證能力，難度較大，學生在短時間內難以理清頭緒.通過GeoGebra軟件作出粒子的運動動態(tài)軌跡，并根據所求問題進行動態(tài)調整，可以化抽象為形象，使復雜問題變得簡單、直觀，學生更容易接受，同時也可以很好地幫助學生養(yǎng)成嚴謹?shù)乃季S習慣，提升其學科核心素養(yǎng).