基于轉矩分配函數的開關磁阻電機的效率優化方法

李孟秋，朱慧玉，高 天，沈仕其，徐宇峰

(湖南大學 電氣與信息工程學院，湖南 長沙 410082)

開關磁阻電機(Switched Reluctance Motor，SRM)由于結構簡單、工作可靠、制造成本低、調速性能優越等諸多優良性能,具有與其他類型電動機競爭的潛在優勢,被認為是未來具有很強競爭力的一種調速電動機[1]。但由于SRM自身的雙凸極結構，導致其具有時變的非線性電磁特性，會帶來轉矩脈動和噪聲、振動等問題[2]，使其無法廣泛應用于傳動系統當中。為了降低SRM的轉矩脈動，國內外研究人員采取了多種控制策略，如轉矩分配函數(Torque Sharing Function,TSF)控制策略[3]、直接轉矩控制[4]、電流預測控制[5]、神經網絡預測控制[6]、自適應控制[7]等。文獻[8]采用遺傳算法，在指數型TSF的基礎上對轉矩脈動進行優化，有效地降低了轉矩脈動，對于轉矩脈動起到了很好的抑制作用，未對銅耗、轉矩-轉速等指標進行綜合考慮。文獻[9]提出了對銅耗和轉矩脈動綜合優化控制的概念，以銅耗作為次級優化目標從TSF族中得到最優的TSF，改善了系統整體的性能。文獻[10]在指數型TSF的基礎上，以轉矩脈動和銅耗最小化為目標進行多目標優化，降低了轉矩脈動。文獻[11]在直線型TSF的基礎上，提出了二次型補償曲線，并以電流變化率和銅耗為優化目標得到最優TSF，有效地降低了峰值電流。文獻[12]利用Tikhonov 參數建立以電流變化率和銅耗為目標的目標函數，得到了多參數的TSF，有效地減少了轉矩脈動與峰值電流。文獻[13]利用電機磁鏈特性，建立以銅耗為目標的目標函數，得到了單參數的TSF，有效地減少了銅耗和計算時間。

雖然以上文獻在一定程度上或降低了電機的轉矩脈動，或減少了電機的銅耗，但在電機實際運行中，需要綜合考慮峰值電流、電流可控性、轉矩脈動和電機效率等因素，并根據電機運行速度的需要，選取適當的控制算法。本文在傳統TSF基礎上，根據SRM的非線性磁鏈特性，建立以瞬時相電流為優化對象的目標函數。利用遺傳算法對目標函數進行迭代計算，得到了參考電流曲線。在不同轉速條件下，以銅耗或轉矩脈動為優化目標，利用遺傳算法對權重參數進行優化，得到最優的參考電流曲線。仿真和實驗論證結果表明，該方法在較低轉速時能有效減小轉矩脈動、在較高轉速時能更好地降低銅耗，比傳統TSF效率更高，換相期間的轉矩脈動更小。

1 TSF

1.1 傳統TSF方法

TSF通過配置函數fk(θ)，將總參考轉矩分配給當前時刻位于不同位置的相位k，作為相參考轉矩。由此可以推導出TSF的解析式，如式(1)、式(2)所示。

Tk(θ)=Treffk(θ)

(1)

(2)

式中,Tref為總參考轉矩；Tk為第k相的參考轉矩,θon、θoff、θov分別為開通角、關斷角、重疊角。由式(2)可知，選取合適的frise和ffall函數可以使電機在換相區間輸出恒定的轉矩。

傳統的直線型TSF如圖1所示。TSF的性能可以通過以下3個方面進行評估：① 電機運行在導通區間所產生的銅耗；② 電機運行時的轉矩脈動；③ 電機運行的效率。

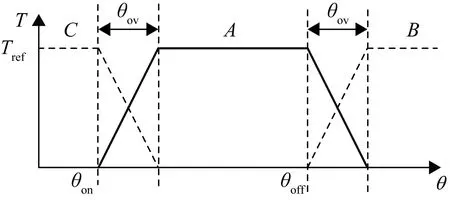
圖1 直線型TSF

1.2 TSF的評估指標

由于SRM的對稱結構，電機的銅耗可以用電流有效值表示，即在導通周期內瞬時相電流積分的均方根表示，如式(3)所示。

(3)

式中，IRMS為繞組電流的有效值；I為繞組電流的瞬時值。當電機轉動時，會產生反電動勢，即由轉子位置改變引起繞組中磁鏈變化的感應電動勢。在低速時，反電動勢產生的影響很小，可以忽略不計。高速時，由于此時轉速較大，則反電動勢對磁通的影響不能被忽略。

忽略繞組電阻的影響，由SRM電路方程可以推導出式(4)，并可以得到電機轉速與繞組磁鏈變化率之間的關系。

(4)

式中，Uk為繞組電壓；ω為電機轉速；λ為電機的磁鏈；I為繞組電流。由式(4)可知，隨著電機轉速的提高，磁鏈的變化率?λ/?θ降低，而為了滿足參考轉矩，則勢必要增加繞組上的電流。這一方面將導致更高的銅耗；另一方面，轉速越高，繞組通電周期越短，運動電動勢就越大，電流沒有充足的時間到達給定值，無法滿足參考轉矩，從而失去了轉矩分配的有效性，使得電機在換相期間產生較大的轉矩脈動。

如式(5)所示給出了轉矩脈動的定義：轉矩脈動可表示為電機導通期間瞬時轉矩脈動積分的均方根。

(5)

SRM的效率為有用功率與總功率之比。

(6)

在轉速恒定且外加電壓不變的情況下，式(6)可以簡化為平均轉矩與繞組電流有效值的正比例函數：

(7)

式中，U，I，η，m分別為外加電壓、母線電流、效率、比例系數。

2 新型TSF

在本節中，提出一種新型轉矩分配方法。通過結合電機的磁鏈特性和轉矩特性，將轉矩分配問題轉化為一個最優化求解問題。并通過離線求解該問題，得到滿足最優條件的TSF。

由式(3)可知，銅耗與瞬時相電流成正相關，而在電流換相區，存在多相電流同時產生銅耗，為了最大限度地降低銅耗并降低計算難度，本文以瞬時相電流為優化目標在換相區間建立最優化問題模型。

在換相區間，繞組上同時存在開通相電流和關斷相電流。由于關斷相需要一定退電流的時間，使得關斷相電流過大時產生負轉矩。本文通過引入權重參數σ抑制關斷相電流，建立的最優化目標表示為

(8)

式中，Ik和Ik-1分別為位于電流重疊區間繞組上的開通相電流和關斷相電流；J為目標函數的目標值。在求取最小的J的過程中，隨著σ增大，放大了關斷相電流對目標函數結果的影響，為了使J最小，關斷相電流隨之減小，達到抑制關斷相電流的效果。

而且相電流的優化跟蹤必須考慮以下3個約束。

① 由于不同電機具備不同的電流承受能力，使得電流不能無限制的增大，所以電流應處在電流額定范圍內，即

0≤Ik,k-1≤Irated

(9)

式中,Irated為電流額定值。

② 優化函數應滿足轉矩特性，即

Tref=T(Ik,θk)+T(Ik-1,θk-1)

(10)

其中，總參考轉矩Tref由開通相和關斷相提供；相轉矩T(I,θ)是轉子位置和相電流的函數，通過查表法可進行數據的查詢處理，T(I,θ)曲線如圖2所示。

圖2 SRM的T(I,θ)曲線

③ 聯立電機電壓方程和磁鏈特性，可以得到SRM的動態特性，以確保跟蹤當前電流模型。

(11)

式中，U，R，I，λ，Δt分別為電源電壓、繞組電阻、相電流、磁鏈和采樣時間。這個條件使得產生電流的相電壓在閾值電壓的范圍內，并在采樣時間內限制電流變化率。當此約束與其他約束同時滿足時，可以在磁鏈限制范圍內跟蹤電流基準，使轉矩脈動最小。

電機驅動可動態控制相位電壓，使電流變化率與參考電壓變化率相匹配。為了得到更好的電流跟蹤效果，本文采用了電流預測控制方式跟蹤參考電流，進一步降低由于電流跟蹤效果差導致的轉矩脈動。

因遺傳算法具備計算簡單、全局尋優能力強等特點，本文采用多重嵌套的遺傳算法計算該最優化問題，得到具有最優結果的參考電流剖面及相對應的權重參數。

3 權重參數的選擇

為了降低銅耗并滿足參考轉矩的需求，需在能產生極大轉矩的相位產生激勵電流。而對齊位置之前的激勵電流遠遠大于該位置之后的激勵電流。因此，當激勵電流的相位越超前時，電機銅耗就越高；但是在對齊位置后激發相位，將會導致負轉矩的產生。這表明，在選取激發相位時應結合獲取最低銅耗和減少負轉矩產生這兩種需求選擇平衡點。隨著電機轉速的升高，將會導致導通周期變短、感應電動勢增大等情況出現，使得實現這種平衡變得愈發困難。

本文在目標函數中引入權重參數σ，增加了選取激發相位的靈活性。隨著σ值的增大，目標函數中的關斷相電流會受到更大的抑制作用，進一步降低關斷相在對齊位置附近的轉矩。圖3和圖4為在12/8極SRM仿真模型上設定Tref=4 N·m、轉速在100 r/min和600 r/min(高速)的情況下，不同σ條件下的電流曲線和相轉矩波形，電流限幅為60 A。

由于較高的σ值會抑制關斷相電流，為滿足優化約束(式(9))，將導致導通相電流加大；為了使導通相電流增大，則需超前激發相位。簡而言之，增加σ會導致激發相位提前。為了使得電機可以根據需求在高轉速下運行，應提前激發相位。

分析圖3和圖4可知，電機在低速運行時，為了得到滯后的參考勵磁電流，應選取一個較低的σ值，從而獲得較低的峰值電流并降低銅耗；在高速運行時，為了提前激發相位，需要選取一個較大的σ值，從而抑制負轉矩的產生。

圖4和圖3對比可得，相電流在高速時的變化率顯著低于其在低速時的變化率。這是由于在本文所提出的最優化問題中，將電機磁鏈特性作為約束條件，從而限制電流變化率，增強電流跟蹤能力。而電機運行在高速時，電流變化率較低，如果沒有選取足夠高的σ值使得激發相位超前，則會產生電流拖尾的現象，使得退電流過程在負轉矩區工作，導致負轉矩的產生。

圖3 轉速為100 r/min、Tref=4 N·m時的數據

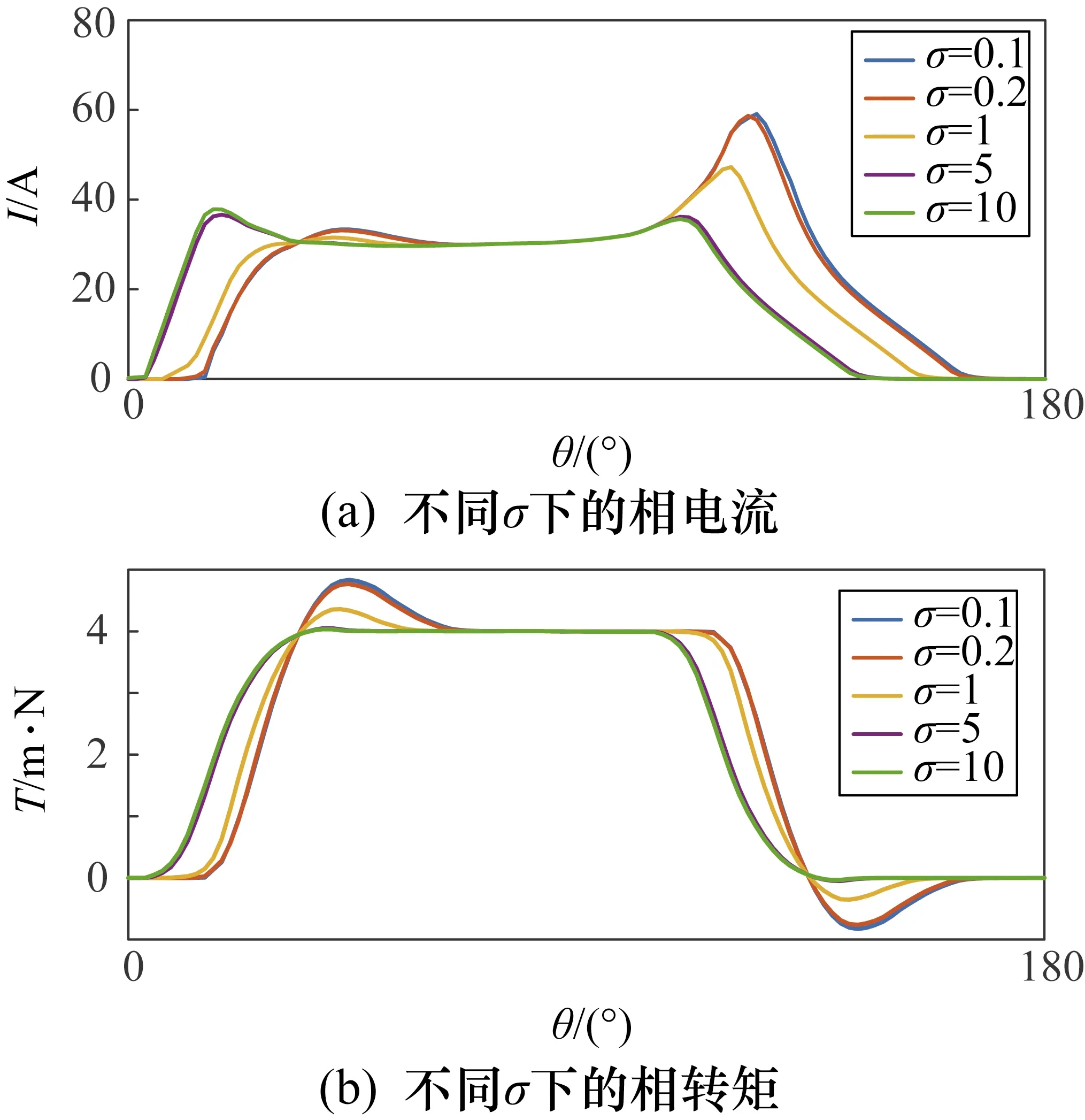
圖4 轉速為600 r/min，Tref=4 N·m時的數據

將上述所得的參考電流曲線用于仿真，比較不同σ下的銅耗與轉矩脈動，可以獲取到Tref=4 N·m、不同轉速下的輸出結果，如表1所示。

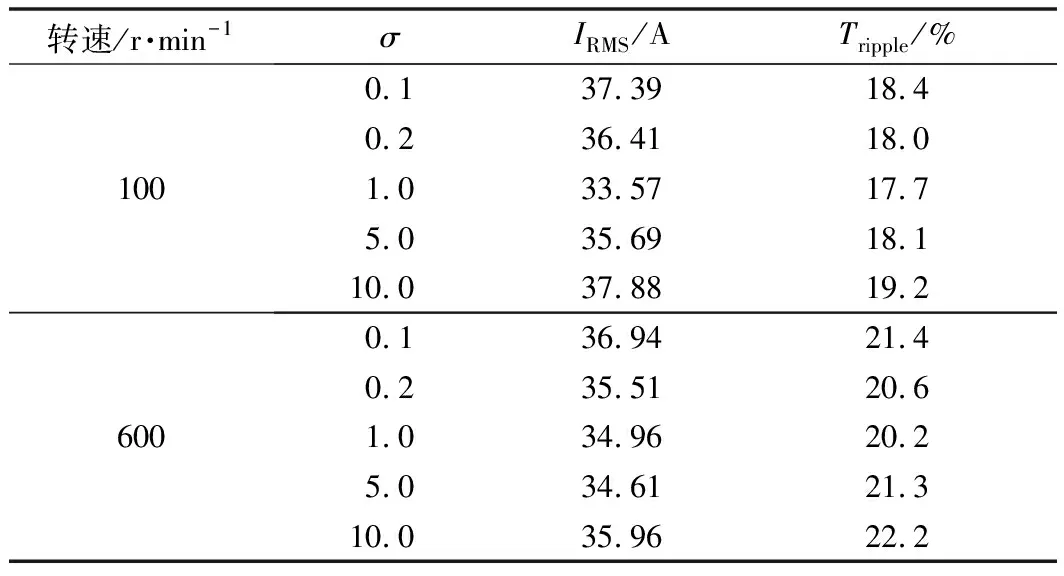
表1 不同轉速下σ對TSF動態特性的影響

由于電機模型實際電機之間存在誤差，使得輸出數據也會有些許偏差。由表1可以看出，低速時，為了使銅耗最小，σ的取值范圍應在0.2～5之間，并使得轉矩脈動最小。轉速較高時，σ的取值應大于5，從而在電機承受范圍內減少負轉矩的產生。

值得注意的是，當σ值增大時，激發相位提前且峰值電流將隨之增大，如表1所示。這是由于未對齊位置附近的轉矩變化率很低，需要極大的激發電流才能滿足Tref。因此，除了要考慮銅耗之外，還需根據電機的實際限制和電機驅動的具體要求，為選取最佳參考電流曲線附加限制。為了選取較為精確的σ，本文采用遺傳算法對σ進行篩選。

4 仿真與分析

為了驗證TSF，本文搭建了額定功率為1.5 kW的12/8極SRM的電機模型，并對此進行了仿真分析，選取Tref=4 N·m。

為了驗證本文所提出的新型TSF的性能，將該TSF與傳統TSF在相同條件下進行了對比分析。

4.1 新型TSF的參數識別和性能評估

對于新型TSF，本文在轉速和轉矩恒定的條件下，使用遺傳算法多次迭代，獲取滿足約束條件的σ值及參考電流，控制框圖如圖5所示。

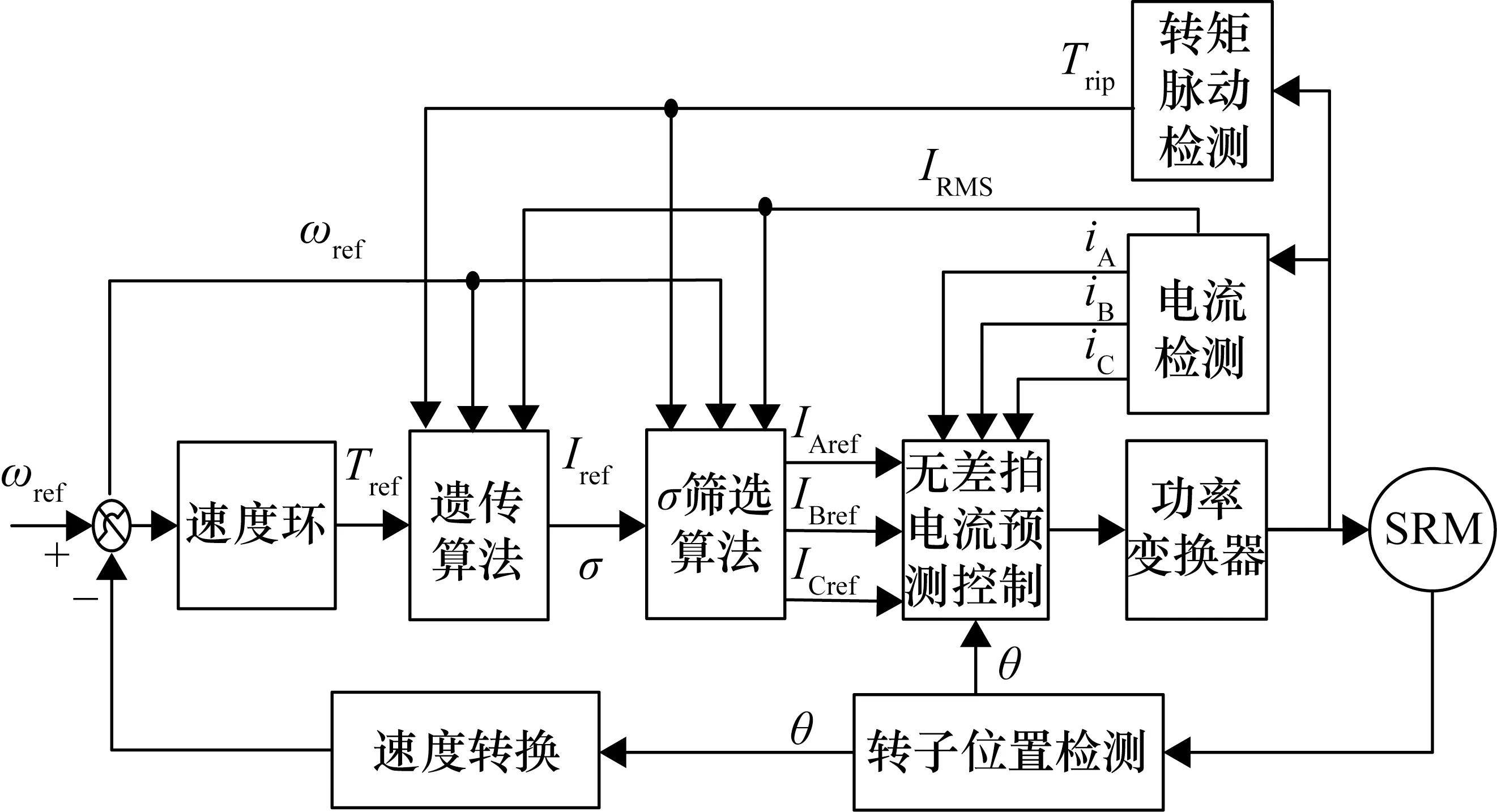
圖5 SRM控制框圖

采用遺傳算法為外部循環優化算法，將當前參考轉速、參考轉矩、輸出銅耗及對應轉矩脈動作為遺傳算法的輸入端，并將新型TSF作為優化目標，得到當前轉速與參考轉矩下的不同σ及其最優I(θ)曲線族。

將所得到的σ對應的I(θ)作為σ篩選算法的輸入端；并根據當前轉速的不同，設置對應的篩選條件：低速時以轉矩脈動最小為篩選條件，高速時以銅耗最小為篩選條件，從而得到最優參考電流曲線。

4.2 電流跟蹤

本文采用電流預測控制方式進行電流跟蹤，并對比了不同轉速、不同權重下的電流跟蹤效果。

如圖6、圖7為采樣頻率為10 kHz條件下，分別在100 r/min和600 r/min轉速下,權重參數不同時的電流跟蹤效果。

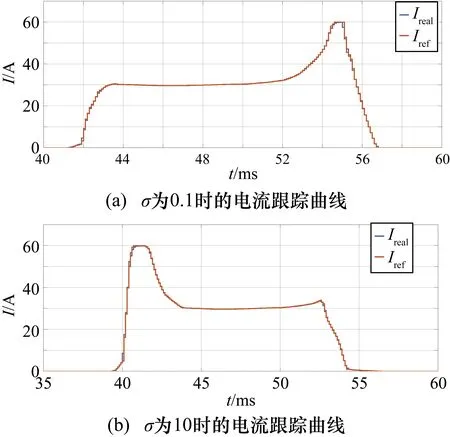
圖6 轉速為100 r/min時電流跟蹤曲線

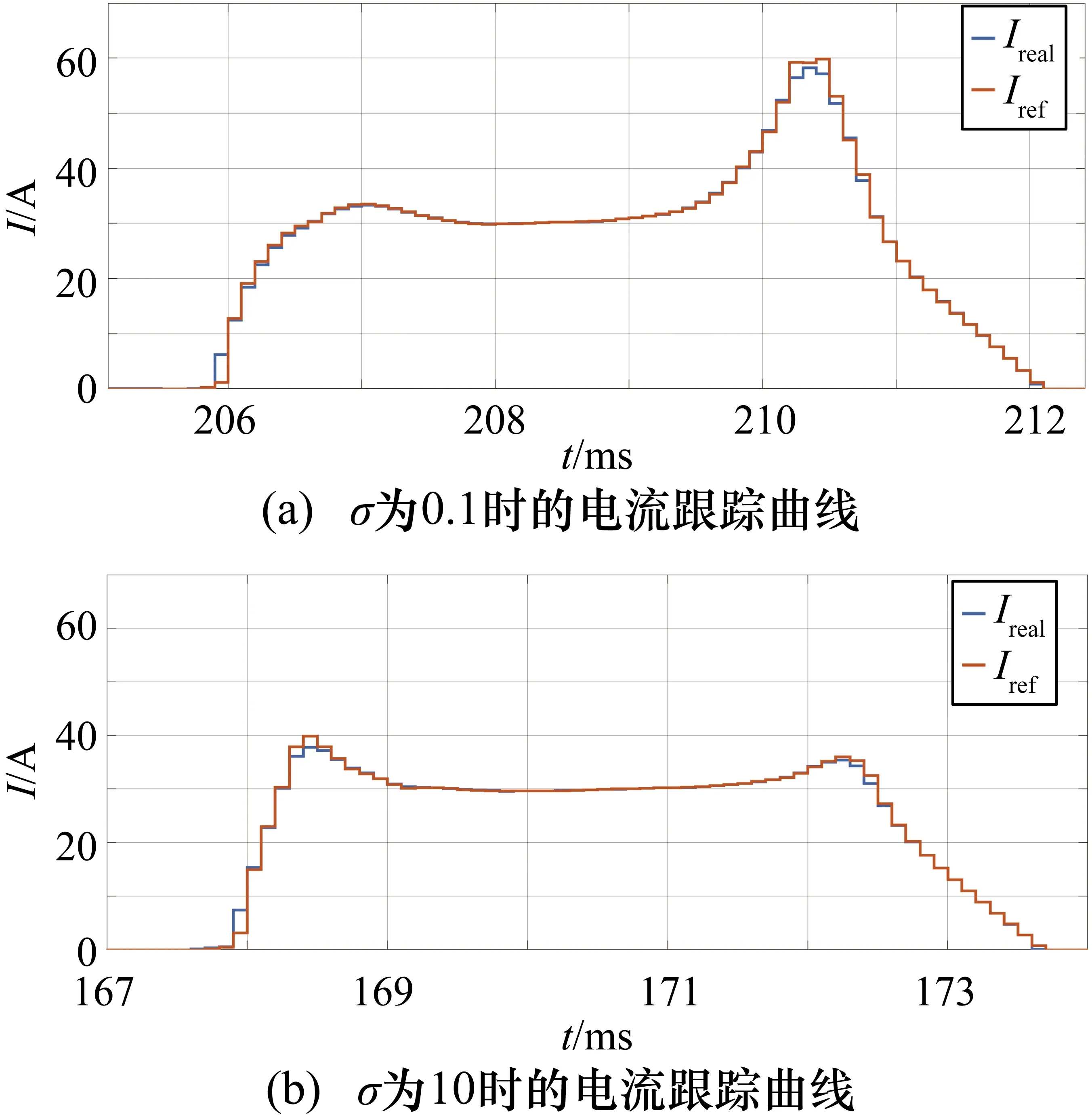
圖7 轉速為600 r/min時電流跟蹤曲線

由圖6可知，采用電流預測控制跟蹤電流后仿真的輸出電流與參考電流曲線在低速情況下基本相同，其跟蹤誤差并不隨σ變化而變化。對比圖6和圖7可知，隨著轉速的升高，參考電流曲線也會相應地限幅，加強電流跟蹤效果。

4.3 新型TSF的動態仿真

當Tref=4 N·m、采用電流預測控制跟蹤電流且轉速分別為100 r/min和600 r/min時，采用傳統TSF和新型TSF之間的數據對比如表2所示。

根據表2數據分析可得，在較低轉速時傳統TSF中余弦型TSF具備較低的轉矩脈動，且新型TSF的轉矩脈動略低于余弦型TSF的轉矩脈動，此時σ=1；而在較高轉速下，傳統TSF方法中余弦型TSF具備最低的IRMS，且新型TSF的銅耗略低于余弦型TSF，此時σ>5。

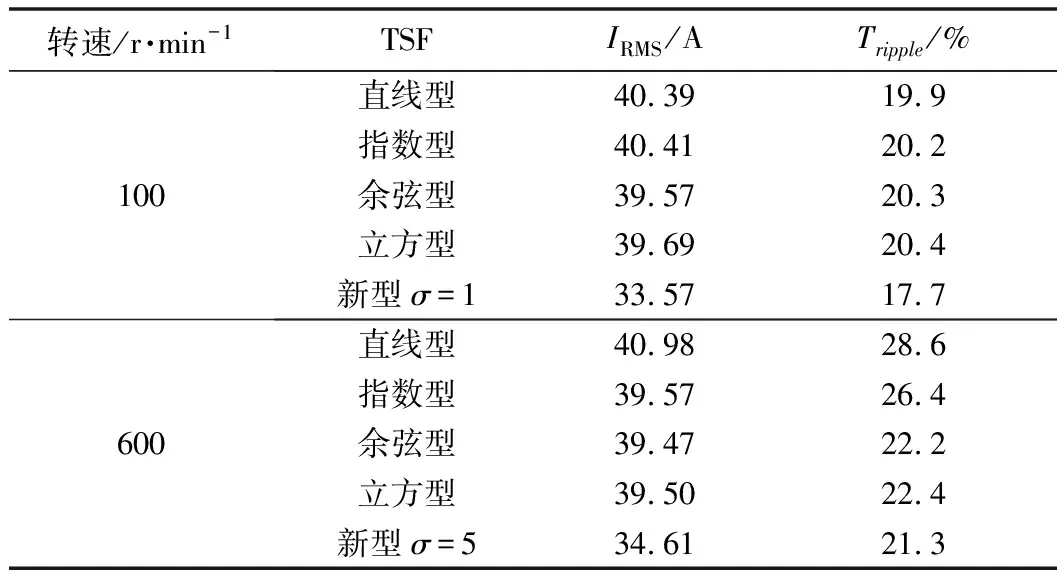
表2 不同轉速下不同TSF曲線的電機特性

轉速為100 r/min時，采用直線型TSF的相電流與總轉矩如圖8(a)所示，新型TSF的相電流和總轉矩如圖8(b)所示。

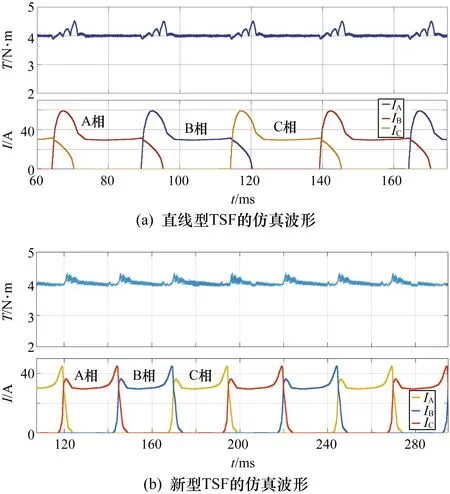
圖8 100 r/min時不同TSF的仿真對比

由圖8可知,采用新型TSF控制結合電流預測控制相較于直線型TSF控制可以在較低轉速有效地抑制轉矩脈動，加強電流跟蹤效果，并且降低換向期間的電流峰值，使得電機在較低轉速下既能降低轉矩脈動，也可以提高效率。

轉速為600 r/min時，采用余弦型TSF的相電流與總轉矩如圖9(a)所示，新型TSF的相電流和總轉矩如圖9(b)所示。

由圖9可知采用新型TSF控制結合電流預測控制相較于余弦型TSF控制方式可以在較高轉速下加強電流跟蹤效果，并且降低換向期間的電流峰值，提高了效率。

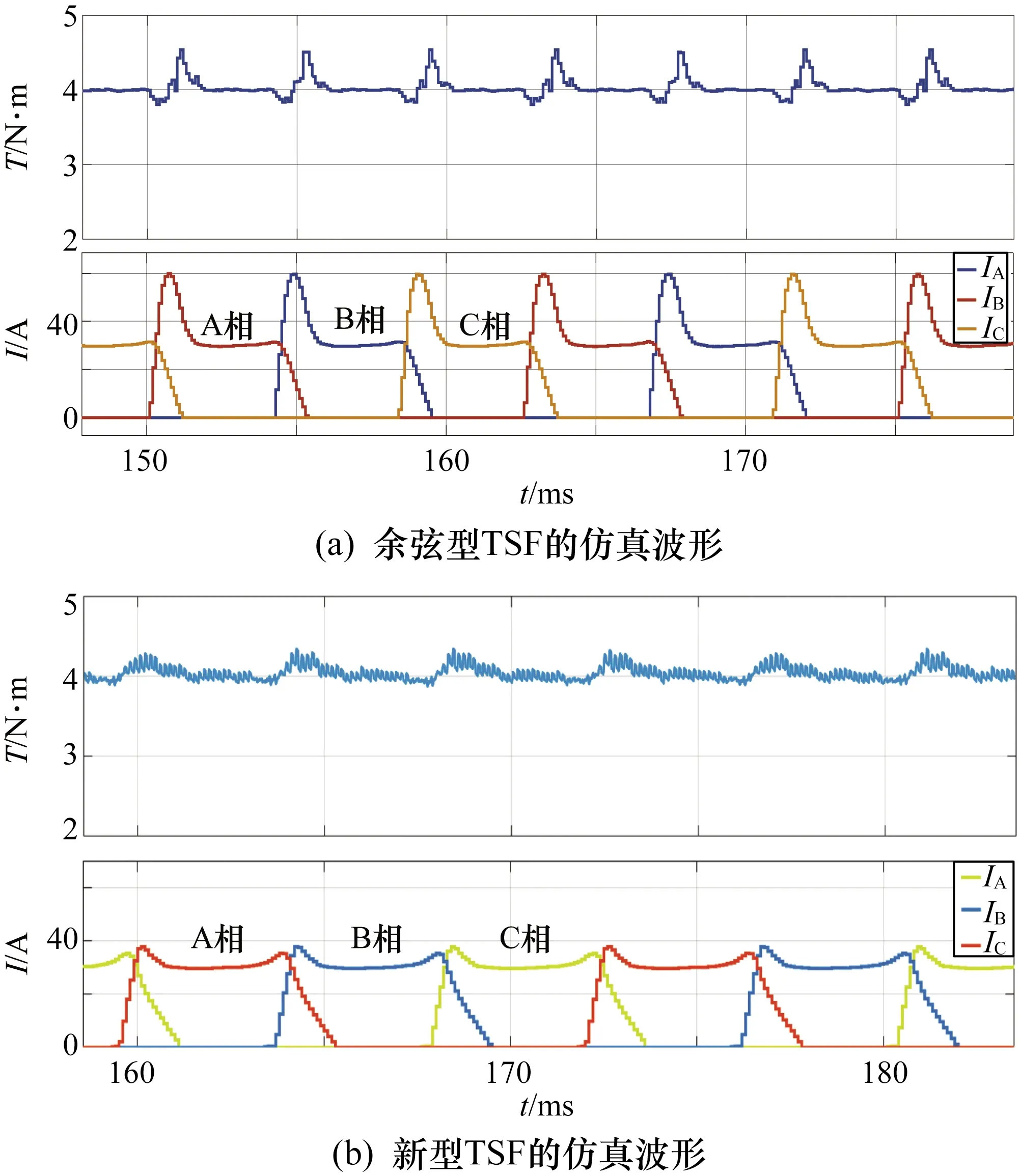
圖9 600 r/min時不同TSF的仿真對比

5 實驗驗證

該方法在額定功率1.5 kW的12/8極三相SRM上進行了實驗驗證，其中直流電源電壓US為72 V、開關頻率為10 kHz、磁粉制動器的負載轉矩為4 N·m。實驗平臺如圖10所示，主控芯片為TMS320F28335的DSP控制系統。分別在電機轉速100 r/min和600 r/min的情況下，對新型TSF和傳統TSF進行對比性實驗。

圖10 實驗平臺

轉速為100 r/min時，采用直線型TSF的相電流與總轉矩如圖11(a)所示，新型TSF的相電流和總轉矩如圖11(b)所示；轉速為600 r/min時，采用余弦型TSF的相電流與總轉矩如圖12(a)所示，新型TSF的相電流和總轉矩如圖12(b)所示。

由圖11可以明顯看出，在100 r/min時，采用新型TSF的轉矩脈動要低于采用傳統TSF。而在圖12中，傳統TSF的峰值電流為62 A，新型TSF的峰值電流為38.2 A，銅耗有所減小。

圖11 100 r/min時不同TSF的實驗對比

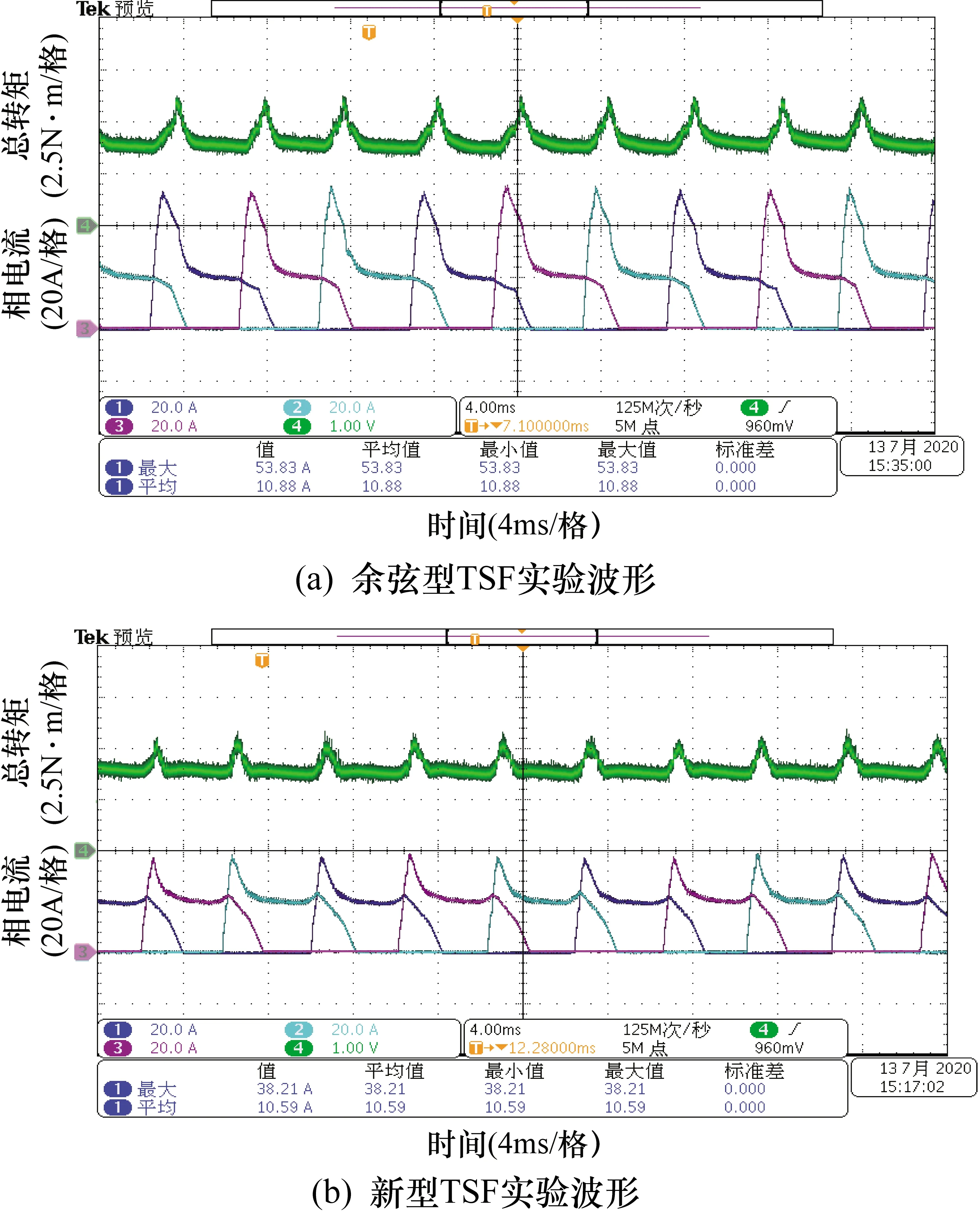
圖12 600 r/min時不同TSF的實驗對比

圖11、圖12是采用了電流預測控制跟蹤的實驗波形，相較于仿真數據而言，其相電流幅值在非換向區較小，這是因為在實際情況下，電機的電感系數會隨著電機使用時間的增加或安裝造成的誤差而改變，與標定的電機參數存在誤差，使得基于數據表的模型預測控制的精準性降低。

Tref=4 N·m時,采用不同TSF的電機性能如表3所示。

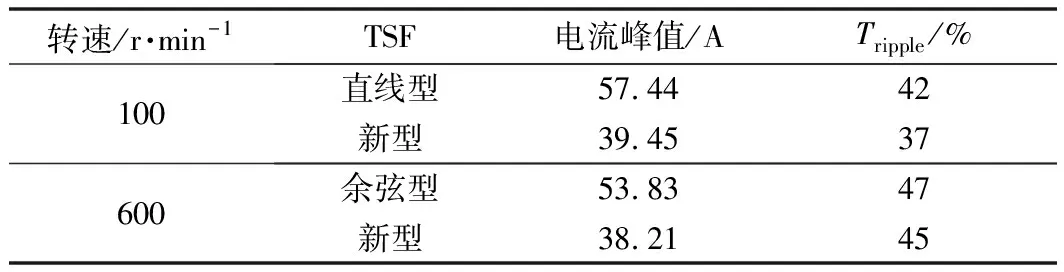
表3 不同轉速下不同TSF的電機性能

根據實驗與仿真結論的相對一致性可知，基于TSF的SRM的效率優化方法具備有效性。

6 結束語

由于SRM在運行時存在電流峰值過高、電流可控性下降等問題，使得銅耗較高、轉矩脈動較大。本文提出了一種基于TSF的SRM的效率優化方法。依據SRM的電機特性獲取新型TSF，并根據轉速變化的需求，綜合考慮后選取轉矩脈動與銅耗作為控制參數進行優化，從而得到最優的參考電流曲線，并通過電流預測控制跟蹤參考電流，提高了電流的可控性。仿真和實驗表明，優化后的新型TSF可以在較低轉速下降低轉矩脈動，在較高轉速下能有效地提升運行效率。但同時該方法對電機參數較為依賴，日后在這一方面需進行改進。