行星輪系動力學分析與響應表示方法研究

吳守軍，馮輔周，吳春志，矯英祺

（1.63963部隊，北京100072；2.陸軍裝甲兵學院車輛工程系，北京100072；3.32379部隊，北京100072）

引言

集中參數模型具有建模過程簡單、求解速度快等優點，在行星齒輪動力學分析中得到廣泛應用［1］。依據自由度數量可將集中參數模型分為純扭轉模型［2］、平移-扭轉模型［3］和橫-扭-擺耦合模型［4］。Inalpolat等［5］建立了行星齒輪平移-扭轉模型，利用單個嚙合力信號研究了齒輪制造誤差對嚙合頻率邊帶成分的影響，并結合Hanning窗權重函數近似表示齒圈測點的加速度信號；程哲［6］建立了直升機行星齒輪傳動系統的純扭轉動力學模型，并獲得太陽輪-行星輪和太陽輪-行星架相對位移響應，以此表示系統的整體響應。僅通過單嚙合副的響應表示系統響應，容易造成系統整體信息的損失，不利于響應機理的研究。楊文廣等［7］將內齒圈最高點的垂直方向加速度作為行星齒輪的系統響應，用于行星齒輪故障特性的仿真分析；桂勇等［8］考慮行星齒輪所有嚙合副的相對位移，分別與各個嚙合剛度相乘，再結合構造的路徑傳遞函數，用于表示行星齒輪系統的響應；雷亞國等［9］考慮信號傳遞路徑效應，將太陽輪豎直方向加速度、太陽輪-行星輪相對加速度及齒圈-行星輪相對加速度在豎直方向分量疊加，作為行星齒輪系統的加速度響應。該方法較為復雜，涉及較多的箱體結構，相關的系數難以確定，且多對嚙合副的嚙合線相對加速度在y方向疊加會產生抵消（選擇此方法與本文對比）；Liang等［10］將改進的漢明窗函數與行星輪加速度相乘，再將各個行星輪的響應疊加，作為行星齒輪系統的整體響應。本文的太陽輪固定，信號不存在路徑調制，因此該方法不適用；Parra等［11］將集中參數模型的行星輪-齒圈嚙合力分解到y方向，結合行星輪到測點的路徑調制，將各個嚙合力分量求和，作為行星齒輪系統測點的響應。該方法計算嚙合力時沒有考慮嚙合阻尼，且嚙合力y方向分量疊加時主要成分會相互抵消，所得信號規律不明顯（選擇此方法與本文對比）；Xue等［12］建立了行星齒輪集中參數動力學模型，并利用有限元法計算嚙合剛度，利用行星架轉速信號實現故障診斷，避免了傳遞路徑對信號的調制；Bacem等［13］提出了一種新的行星齒輪建模方法，建立了傳遞路徑的模型，從傳感器的視角表示構件的位移，通過實驗信號頻譜驗證了所提方法的正確性。

上述學者建立的行星齒輪集中參數模型均為齒圈固定的情況，針對太陽輪固定的情況尚未見研究。本文以某型坦克變速箱的K3行星排為研究對象，考慮時變嚙合剛度、嚙合阻尼、支撐剛度、支撐阻尼及嚙合相位差等非線性因素，建立其平移-扭轉動力學模型，提出一種太陽輪固定的行星齒輪系統響應表示方法，并通過仿真響應和實驗信號的嚙合頻率、故障頻率驗證了模型的正確性。

1 行星齒輪動力學建模

某型行星變速箱Ⅳ擋時的結構原理如圖1所示。K3行星排齒輪的模數為5 mm，壓力角為20°，楊氏模量為2.06×1011Pa，泊松比為0.3，詳細參數如表1所示。

表1 K3行星排齒輪參數Tab.1 Planetary gear parameters of K3

圖1 行星輪系結構原理（單位：mm）Fig.1 Schematic diagram of planetary gear（Unit：mm）

K3排構件的轉速關系為

式中ns為太陽輪轉速，nr為齒圈轉速，nc為行星架轉速，zr為齒圈齒數，zs為太陽輪齒數。

行星輪系嚙合頻率為

式中z為參考齒輪的齒數，nc為參考齒輪相對于行星架的轉速。

故障頻率ffault為式中Z為故障齒輪的齒數。

1.1 平移-扭轉動力學建模

K3排 由太陽輪s3、行星輪p?l、齒圈r和行 星架c組成，行星輪對稱不均勻分布，行星輪布局與平移-扭轉動力學模型如圖2所示。kbs3，cbs3分別為太陽輪支撐剛度與支撐阻尼；kbc，cbc分別為行星架的支撐剛度與支撐阻尼；kbr，cbr分別為齒圈的支撐剛度與支撐 阻 尼；kbp?l，cbp?l分 別 為 行 星 輪 的 支 撐 剛 度 與 支 撐 阻尼；根據文獻［14］，支撐剛度取1×108N/m，支撐阻尼取1.5×103N·s/m；kus3，cus3分別為太陽輪扭轉剛度和扭轉阻尼；kuc，cuc分別為行星架的扭轉剛度與扭轉阻尼；kur，cur分別為齒圈的扭轉剛度與扭轉阻尼；ks3p?l，cs3p?l分 別 為 太 陽 輪-行 星 輪 嚙 合 剛 度 和 嚙 合阻 尼；φp?l為 行 星 輪p?l的 位 置 角，φp?l=[0，48°，120°，168°，240°，288°］。

圖2 K3行星排示意圖Fig.2 K3 planetary row diagram

相對位移使得嚙合線拉伸為正，反之為負；中心構件受到的支撐力與位移方向相反；行星輪受到的支撐力與位移方向相同。根據牛頓第二定律建立各個構件的運動微分方程如下：

太陽輪

行星架

齒圈

行星輪

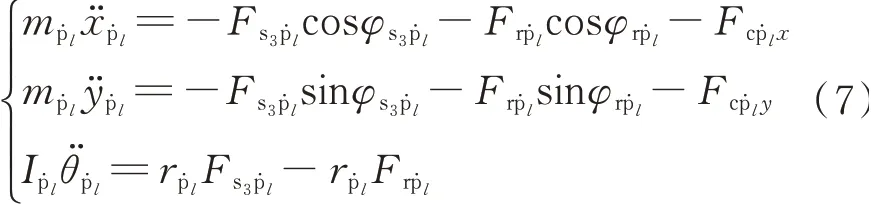
式中mj和Ij分別代表各構件的質量和轉動慣量；xj和yj代表平動位移；θj代表角位移；rbj為中心構件的基圓半徑或行星輪中心到行星架中心的距離（j為s3，c，r，p?l）；Fg代表各嚙合副嚙合力（g為嚙合副s3p?l，rp?l）；Fbjx，Fbjy代 表中心構件的支 撐 力；Fcp?l x和Fcp?l y代表行星輪受到的支撐力；Fus3為太陽輪受到的扭轉支 撐 力，Fus3=cus3θ?s3+kus3θs3；φs3p?l表 示 太 陽 輪 與 行星輪 的 相 對 嚙 合角，φs3p?l=φp?l+α0+π/2；φrp?l表 示行星輪與齒圈的相對嚙合角，φrp?l=φp?l-α0+π/2；α0為壓力角；Tin，Tout分別為輸入、輸出轉矩。

將各個構件的方程合并，得到微分方程矩陣形式如下

式中M為質量矩陣；Cm為嚙合阻尼矩陣；Cb為支撐阻尼矩陣；Km為嚙合剛度矩陣；Kb為支撐剛度矩陣；Q為位移矩陣；T為負載矩陣。

其中，Cbs3=diag[cbs3cbs3cus3]，其余構件支撐阻尼類似。

嚙合阻尼矩陣各個子矩陣的具體表達式如下：

其中，Qs3=[xs3ys3us3]T，其余構件位移類似。嚙合剛度、支撐剛度矩陣元素的詳細表達式與嚙合阻尼、支撐阻尼的形式相同，只需將所有的c替換為k，C替換為K即可。

1.2 嚙合剛度與相位差求解

嚙合剛度是行星齒輪主要的內部激勵，常見的計算方法有方波法［15］、勢能法［16］、有限元法［17］和實驗法［18］。方波法考慮了單雙齒交替嚙合對剛度的影響，但沒有考慮嚙合點變化過程中剛度的變化；勢能法將齒輪的單個輪齒視為懸臂梁，考慮了齒輪嚙合點的變化過程和嚙合剛度的構成，采用積分法計算嚙合剛度，計算效率高，結果較為精確。有限元法借助有限元模型、彈性體局部接觸點變形分析實現嚙合剛度評估，嚙合剛度精度受到有限元模型精度的影響，計算效率較低。實驗法需要在齒輪上粘貼應變片，通過應變測量實現嚙合剛度評估，應變片粘貼的位置、質量、敏感度均會影響測量結果，且實驗周期較長、成本高。

本文采用勢能法估算嚙合剛度，齒輪嚙合剛度由四部分組成：輪齒彎曲剛度、剪切剛度、軸向壓縮剛度和赫茲接觸剛度。K3排太陽輪、行星輪的齒數均小于42（齒根圓小于基圓），嚙合剛度計算公式見參考文獻［19］。K3排太陽輪-行星輪嚙合副、行星輪-齒圈嚙合副在齒輪正常狀態下的嚙合剛度如圖3所示。由圖可知，兩種嚙合剛度均呈現出周期性單雙齒交替嚙合的特點，行星輪-齒圈重合度（εpr=1.73）比太陽輪-行星輪重合度（εsp=1.57）大，因此行星輪-齒圈嚙合副的雙齒嚙合時間較長。兩種嚙合副的嚙合剛度范圍為（1-1.6）×109N/m，可知，支撐剛度不僅不滿足大于嚙合剛度的10倍，還小于嚙合剛度，因此需要采用平移-扭轉動力學模型。

圖3 正常狀態下嚙合剛度Fig.3 Meshing stiffness under normal condition

太陽輪齒根50%裂紋時，太陽輪-行星輪嚙合剛度如圖4所示。太陽輪相對于行星架每轉一周，太陽輪裂紋齒輪依次與6個行星輪各嚙合一次，因此，存在6次嚙合剛度降低。根據行星輪位置角可知，相鄰兩個行星輪與太陽輪故障齒嚙合間隔有兩種：小間隔（行星輪1與行星輪2、行星輪3與行星輪4、行星輪5與行星輪6）、大間隔（行星輪2與行星輪3、行星輪4與行星輪5、行星輪6與行星輪1），兩種間隔分別為4和6個嚙合周期；行星輪-齒圈嚙合副的嚙合剛度與正常狀態相同。

圖4 太陽輪裂紋時太陽輪-行星輪嚙合剛度Fig.4 Meshing stiffness of sun-planet gear with sun gear crack

嚙合相位對行星齒輪系統動力學特性和振動響應具有重要影響［20］。行星齒輪系統含有多個嚙合副，同類型嚙合副的嚙合剛度變化規律一樣，但嚙合剛度之間存在相位差。相位差有同類型嚙合副和不同類型嚙合副兩種。選擇第一個太陽輪-行星輪嚙合副的節點為相位參考點，初始時刻相位為0，相位差的單位為嚙合周期，取值范圍為（-1，1）。計算得到K3排同類型嚙合副的相位差為0，太陽輪-行星輪嚙合副相對于行星輪-齒圈嚙合副的相位差為-0.1716。考慮嚙合相位差時，從節點開始的嚙合剛度如圖5所示。由圖可知，相位差為38.41°-34.56°=3.85°，理論計算的相位差超前0.1716×360°÷15=4.12°，兩者基本一致，誤差是由程序運算將相位差轉換為點數時需要四舍五入造成的。

圖5 節點開始的嚙合剛度Fig.5 Meshing stiffness from pitch node

1.3 平移-扭轉模型必要性分析

純扭轉模型只考慮構件的旋轉自由度，相對平移-扭轉模型簡單，計算效率高。但在嚙合剛度與支撐剛度之比小于10的情況下，純扭轉模型不能準確反映行星齒輪系統的固有特性，而仿真響應與系統的固有特性緊密相關。為了進一步說明建立平移-扭轉模型的必要性，對純扭轉模型和平移-扭轉模型的相對位移和嚙合力響應進行比較分析。

太陽輪-行星輪嚙合線的相對位移表達式為

行星輪-齒圈嚙合線的相對位移表達式為

其中傳動誤差計算公式為

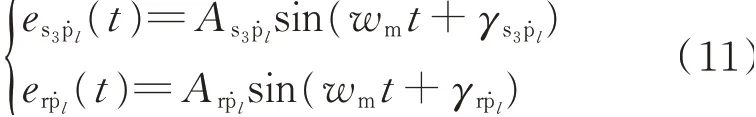
式中Ag為傳遞誤差變化幅值；wm為K3行星排嚙合頻率；γg為傳遞誤差初相位。

引入齒側間隙后，相對位移對應的非線性函數計算公式為

式中b為齒側間隙的一半。

行星齒輪微分方程為剛性方程，ode15s函數使用可變階次的數值微分算法，適合解剛性微分方程。利用MATLAB的函數ode15s求解行星齒輪運動微分方程，相對誤差取1×10-6，絕對誤差取默認值1×10-6。每個嚙合周期采樣點取50，為了提高仿真效率和頻率波形分辨率，輸入轉速設為60 r/min，根據嚙合頻率和故障頻率計算公式，當輸入構件齒圈轉速為60 r/min時，K3排 嚙合頻率fm3=21.18 Hz，太陽輪故障頻率fs3=4.24 Hz。仿真步長為1/50/21.18=9.44×10-4s，采樣率為1060 Hz，仿真時間為行星架周期Tc（1.416 s）。

齒輪正常狀態下，純扭轉模型的太陽輪-行星輪嚙合線和行星輪-齒圈相對位移響應及頻譜如圖6所示。相對位移變化趨勢與嚙合剛度變化趨勢相反，當嚙合剛度處于峰值時，相對位移處于谷值；頻譜由嚙合頻率及其倍頻構成，一倍頻幅值最為突出。

圖6 純扭轉模型嚙合線相對位移Fig.6 Mesh line relative displacement of pure torsion model

齒輪正常狀態下，平移-扭轉模型的太陽輪-行星輪和行星輪-齒圈相對位移及其頻譜如圖7所示。由圖可知，相對位移具有明顯的周期性，變化規律與嚙合剛度相反。由于考慮了平移自由度，導致相對位移出現一定的波動，幅值約為純扭轉模型的10倍，但整體波動幅度較小。頻譜含有嚙合頻率及其倍頻。

圖7 平移-扭轉模型嚙合線相對位移Fig.7 Mesh line relative displacement of translation torsion model

純扭轉模型得到太陽輪-行星輪和行星輪-齒圈嚙合力如圖8所示，由圖可知，由于齒輪嚙入嚙出導致嚙合剛度瞬變，嚙合力出現明顯的周期性沖擊，沖擊間隔為0.0333 s（Tc/30）；頻譜主要包含嚙合頻率及其倍頻，驗證了模型的正確性。

圖8 純扭轉模型嚙合力Fig.8 Meshing force of pure torsion model

平移扭轉模型的太陽輪-行星輪與行星輪齒圈嚙合力及頻譜如圖9所示。嚙合力幅值約為純扭轉模型的10倍，且較純扭轉模型的嚙合力平穩，在嚙入嚙出后保持一段平穩的過程，更加符合實際情況；頻譜中含有嚙合頻率及其高倍頻，嚙合力頻譜幅值約為純扭轉模型的100倍，由此可見，平移-扭轉模型所得響應信號強度更大。

圖9 平移-扭轉模型嚙合力Fig.9 Meshing force of translation torsion model

上述響應均為單個嚙合副的響應，無法體現行星齒輪系統響應，因此，需要提出反映整個系統響應的表示方法。

2 響應表示方法與實驗驗證

2.1 響應表示方法

集中參數模型響應表示的合適與否，對于后續行星齒輪故障機理研究具有重要影響。在實測信號中，箱體表面測點信號包含所有齒輪嚙合點的振動信息，信號由齒輪嚙合點傳遞到箱體表面測點可以分為兩個階段，第一階段：齒輪嚙合點到軸承座；第二階段：軸承座到箱體表面測點。第二階段路徑對信號的影響取決于箱體結構和材料特性，主要對信號的幅值產生衰減。第一階段路徑涉及到嚙合點信號的合成，也是行星齒輪集中參數模型響應表示方法提出的出發點。

根據國內外文獻［9，11］可知，典型的行星輪系集中參數模型響應合成方法有以下幾類：（1）各個嚙合線加速度y方向分量疊加；（2）各個嚙合力y方向分量疊加。不同的響應合成方法適用于不同結構的行星輪系，按照相位差是否一致、是否存在路徑幅值調制等，將行星輪系結構分為以下三種：

（1）同類型嚙合副之間存在相位差時，可以考慮相位差、傳遞路徑的幅值調制（若太陽輪固定，沒有傳遞路徑幅值調制）作用，將嚙合線加速度或嚙合力的y方向分量進行疊加，表示行星輪系整體響應；

（2）同類型嚙合副之間不存在相位差時，對于齒圈固定式行星輪系，振動測點位于齒圈上，可以考慮路徑的幅值調制作用，將各個嚙合線加速度或嚙合力的y方向分量疊加，表示行星輪系的整體響應；

（3）同類型嚙合副之間不存在相位差時，對于太陽輪固定式行星輪系，嚙合點到傳感器的距離隨著行星架的旋轉不變化，從而不存在路徑的幅值調制。若直接將各個嚙合副的嚙合線加速度或嚙合力的y方向分量疊加，分量之間會相互抵消，所得響應沒有規律。

論文研究的對象K3排屬于第（3）種結構的行星輪系，本文采用嚙合線加速度直接疊加表示整體響應。為了驗證所提方法的有效性，將所提方法與雷亞國、Parra方法所得響應進行對比，三種方法的歸一化幅值如圖10所示。由時域信號可知，雷亞國方法與Parra方法所得時域信號雜亂無章，沒有周期性，是由于6個嚙合副的加速度、嚙合力的y方向分量相互抵消造成的，而所提方法得到的響應具有明顯的周期性嚙合沖擊特征。由頻譜可知，所提方法的頻譜具有明顯的嚙合頻率及其倍頻，且與理論值一致。而雷亞國、Parra方法所得頻譜沒有出現嚙合頻率及倍頻特征。

圖10 齒輪正常的歸一化響應Fig.10 Normalized response of normal gears

為了驗證所提方法在含故障齒輪動力學模型響應表示中的有效性，以太陽輪50%裂紋為例，三種方法所得行星齒輪系統的歸一化幅值響應如圖11所示。由時域信號可知，三種方法所得的響應均具有周期性特點，每個Tc存在6次明顯的周期性沖擊，即太陽輪故障齒與6個行星輪的嚙合沖擊。根據行星輪分布位置角可知，沖擊間隔有兩種，小間隔為行星輪1與行星輪2與太陽輪故障齒嚙合產生的，時長約為0.1333Tc；大間隔為行星輪2與行星輪3與太陽輪故障齒嚙合產生的，時長約為0.1999Tc。但雷亞國、Parra方法所得響應的齒輪正常嚙合沖擊相互抵消了，所提方法不僅具有故障沖擊，也具有明顯的正常嚙合沖擊。由頻譜可知，所提方法得到的響應頻譜中嚙合頻率倍頻兩邊出現較多的故障邊頻帶。而雷亞國、Parra方法僅在高頻段、低頻段出現故障頻率及其倍頻，沒有嚙合頻率及其倍頻成分。

圖11 太陽輪裂紋的歸一化響應Fig.11 Normalized response of crack in sun gear

綜上可知，本文所提方法在兩種齒輪狀態下所得響應均能夠有效提取嚙合頻率、故障頻率及其倍頻，在太陽輪固定、無相位差的行星輪系結構的響應表示中具有顯著優勢。

2.2 實驗信號驗證

在某型坦克行星變速箱K3行星排太陽輪齒根處受拉力側通過線切割加工深度為5 mm裂紋（50%），裂紋寬度橫貫整個齒寬，裂紋角度與輪齒中線為60°，裂紋故障件如圖12所示。

圖12 太陽輪齒根裂紋Fig.12 Crack in the root of sun gear

實驗設備主要由電機、行星變速箱、液壓站、負載、數據采集儀和控制臺等組成，現場布局如圖13所示。實驗工況為Ⅳ擋，采樣率為20 kHz，將振動傳感器貼于K3行星排上方，采集齒輪正常、K3排太陽輪裂紋兩種狀態的振動數據進行驗證。實驗輸入轉速為1500 r/min，對應行星變速箱的各部分頻率成分如表2所示。

圖13 實驗設備Fig.13 Experimental equipment

表2 Ⅳ擋時行星變速箱的主要特征頻率Tab.2 The main characteristic frequency of planetary transmission in theⅣgear

齒輪正常時，振動信號去直流后的時域波形和頻譜如圖14所示。由圖可知，頻譜幅值較大的頻率成分為定軸輪系嚙合頻率及其倍頻；其次，可以觀察到主泵嚙合頻率、回油泵嚙合頻率及K3嚙合頻率3倍頻（1588 Hz）；放大低頻段0-1100 Hz，可以清晰觀察到K3排嚙合頻率及2倍頻，輸入軸轉頻及其倍頻。

圖14 齒輪正常狀態實驗信號Fig.14 Gear normal state test signal

太陽輪裂紋時，振動信號的時域波形和頻譜如圖15所示。由圖可知，時域信號幅值比正常狀態的稍大；頻譜中除了正常狀態可以觀察的嚙合頻率外，還出現了K3太陽輪故障頻率及其倍頻；還出現了fs3的2/3倍頻（35.2 Hz），這是由K3行星排輪分布特點造成的。

圖15 太陽輪裂紋實驗信號Fig.15 Test signal of sun gear crack

3 結論

針對現有行星輪系集中參數模型響應表示方法不適用于太陽輪固定、無相位差的行星齒輪系統的情況，以坦克行星變速箱K3排為對象，考慮時變嚙合剛度、相位差等因素，建立了太陽輪固定的行星輪系平移-扭轉模型，分析了嚙合相位差對嚙合剛度的影響，通過嚙合線相對位移和嚙合力信號分析了平移-扭轉模型的優勢，并驗證了模型的正確性；提出采用嚙合線加速度直接疊加作為行星輪系整體響應的表示方法。仿真信號和實驗數據驗證結果表明，所提方法得到的信號頻譜包含嚙合頻率、故障頻率及其倍頻成分，與實驗信號的頻率成分一致。而兩種傳統方法在齒輪正常與故障狀態下所得信號頻譜沒有正常嚙合頻率，從而驗證了所提方法的優勢和有效性。