基于DBSCAN聚類和數據篩選的系統諧波阻抗估算

雷達，常瀟，劉子騰，趙軍，張世鋒，徐永海

(1. 國網山西電力科學研究院， 太原 030001； 2. 華北電力大學 新能源電力系統國家重點實驗室，北京102206)

0 引 言

隨著電力電子器件和電力設備的發展，諧波污染問題越來越嚴重，若不進行治理，會給電網帶來很大威脅[1-3]。公共連接點(Point of Common Coupling，PCC)處的諧波通常是由系統側和用戶側疊加產生的，準確劃分諧波責任是控制諧波水平的重要前提，而系統阻抗又是諧波發射水平評估和諧波責任劃分的關鍵參數[4-7]。

目前國內對諧波阻抗估算已經進行了大量研究。波動量法[8-9]適用于背景諧波電壓較平穩的情況，該法通過計算PCC處諧波電壓和電流波動量比值來求解系統阻抗。獨立隨機矢量協方差特性法[10]通過數學變換的方法削弱背景諧波電壓波動項，對背景諧波電壓小范圍波動有一定的抑制作用。盲源分離類算法[11-12]對諧波電壓和諧波電流進行分離，通過混合矩陣和諧波阻抗矩陣之間線性關系求得系統側諧波阻抗，要求源信號具有非高斯性且相互獨立。線性回歸法[13-15]利用戴維南或諾頓等值電路中PCC處諧波電壓和諧波電流關系式，回歸出系統阻抗值。隨著新能源的高占比入網，加劇了電網背景諧波的波動情況，使背景諧波電壓可能發生諧振等短時較大幅度電壓波動[16-17]，上述方法在處理較大范圍諧波電壓波動時效果不佳，此時需要經過數據篩選，才能更準確估算諧波阻抗值。

同時，以上研究均基于系統阻抗恒定的假設。由于等值電路中通常將除關注用戶外的區域計入系統側，因此電力系統運行方式的改變、無功補償方式的變化、投切支路、分布式電源脫網與并網等原因都可能導致系統阻抗發生變化，在計算諧波阻抗時，應首先分析系統阻抗值是否發生變化。

考慮阻抗變化的諧波阻抗估計研究較少，文獻[18]通過加窗一元線性回歸粗估系統諧波阻抗，再用小波變換模極大值法檢測系統諧波阻抗突變點，但當背景諧波電壓波動較大時，系統諧波阻抗粗估值誤差大，此時會干擾對測量數據的分段處理，從而不能精確辨識突變點。文獻[19]提出一種基于斜率辨識諧波阻抗變化的方法，在諧波電壓和諧波電流散點圖中，通過計算斜率值區分阻抗值，但僅適用于背景諧波電壓平穩的條件。

考慮系統諧波阻抗變化和背景諧波電壓波動的情況，采用DBSCAN(Density-Based Spatial Clustering of Applications with Noise)聚類[20-21]分離出諧波阻抗恒定的數據組，再根據復相關性分析篩選出背景諧波電壓較穩定的數據段，最后采用穩健回歸法估算系統阻抗。文中方法中，DBSCAN是一種密度類聚類算法，其相較于劃分和層次聚類法，在非球狀分布散點圖的聚類中具有明顯優勢；復相關性分析可以對多因變量進行總體相關性分析；穩健回歸法能根據數據的殘差分配權重，減弱異常點對數據的影響，可使結果更加精確[22]。

1 諧波阻抗估算模型

在諧波阻抗估計中，通常將除關注用戶以外的區域全部等效為系統側，可得圖1所示的等效電路圖。

圖中，Us和Ic分別為代表系統側等效諧波電壓源和用戶側等效電流源；Zs和Zc分別為系統側和用戶側等效諧波阻抗；Upcc和Ipcc分別為PCC處的諧波電壓和諧波電流。根據圖1可列關系式：

UPCC=ZSIPCC+Us

(1)

根據式(1)將各變量實部和虛部分開，得：

(2)

式中帶有下標x和y的變量分別為其復數形式的實部和虛部。如果Zs和Us均為變量，則難以估算Zs的值，因此，需要篩選出系統阻抗恒定和背景諧波電壓波動較小的數據段，再進行阻抗估計。

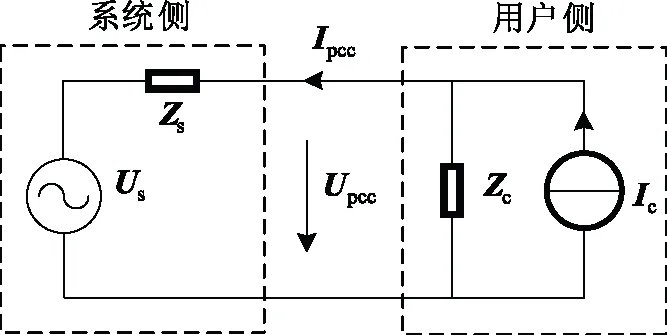
圖1 等效電路圖Fig.1 Equivalent circuit diagram

2 考慮阻抗變化和背景諧波電壓波動的諧波阻抗估算

2.1 DBSCAN聚類篩選

當系統諧波阻抗變化時，需要將不同系統阻抗值對應的數據段區分開，否則會存在很大誤差[23-25]。提出基于DBSCAN聚類的數據分類方法，將系統阻抗相同的數據組聚成一簇，再對每個簇分別進行阻抗估算。

根據式(1)可以看出，以|Ipcc|為橫坐標、|Upcc|為縱坐標構成的散點圖成條狀分布，其斜率與系統阻抗值有關，截距與背景諧波電壓有關，圖2為系統阻抗變化2次構成的散點圖，圖中有3個長條狀分布，分別對應3個系統阻抗值。

圖2 諧波電壓與諧波電流散點圖Fig.2 Spot diagram of harmonic voltage and current

常用的聚類方法大多基于距離聚類，其聚類結果通常是以點為中心的球狀簇，當數據呈非球狀分布時，難以達到預期效果。DBSCAN是一種典型的基于密度的聚類算法，通過尋找高密度區域將數據點分成不同的簇，在DBSCAN聚類中將核心點定義為在對象半徑Eps內含有超過最小數目MinPts的點，該點都在簇內，而邊界點和噪音點是簇外的點，其中對象半徑Eps和最小數目MinPts為給定值。

DBSCAN聚類步驟如下：

(1)數據集D中的所有對象標記為未處理狀態；

(2)檢查數據集D中的每個對象p的Eps鄰域NEps(p)，檢查NEps(p)包含的對象數是否小于最小數目MinPts，如果是進入步驟(3)，如果否進入步驟(4)；

(3)標記對象p為邊界點或噪聲點；

(4)標記對象p為核心點，并建立新簇Ci，將NEps(p)中未歸入任何一個簇的對象加入Ci；

(5)檢查是否所有對象p已經歸入某個簇或標記為邊界或噪聲點，如果否,回到步驟(2)，如果是，輸出結果。

2.2 復相關性分析篩選原理

進行聚類后，對每個簇分別求解諧波阻抗值。當背景諧波電壓存在較大范圍波動時，難以精確估計系統阻抗的值，為了提高估算精度，提出基于復相關性分析的數據段篩選方法。

復相關系數能反映因變量和全體自變量之間的線性關系，以式(2)中第一個式子為例，Upcc-x為因變量，Ipcc-x和Ipcc-y為自變量，其值越趨近于1表明Upcc-x和Ipcc-x和Ipcc-y整體的相關性越高，而由式(2)可知背景諧波電壓波動較小時，其線性關系強烈，復相關系數接近1，此時估計出的諧波阻抗值較精確。反之，越趨近于0,表明相關性越低。故可通過篩選諧波電壓和電流具有較高復相關系數的數據段，來提高諧波阻抗估算值的精確程度。

以y代表Upcc-x，x1和x2代表Ipcc-x和Ipcc-y，計算因變量y與其他兩個變量x1,x2總體的相關程度，需要構造一個關于x1,x2的線性組合，用y對x1,x2做回歸得到：

(3)

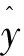
(4)

式中R為y和x1,x2間的復相關系數。

保留R趨向于1的數據段，即篩選出背景諧波電壓波動相對較小的諧波電壓和諧波電流組。

2.3 基于bisquare權重的穩健回歸法

為減小“異常點”的作用，提出在DBSCAN聚類和復相關性篩選后采用基于bisquare權重的穩健回歸法進行系統阻抗估算。

穩健回歸法根據各數據點殘差不同施加不同的權重wi，是一種特殊的加權最小二乘估計，數據點殘差越大，所分配的權重值越小。該法能通過不斷迭代改進權重系數，可以有效減弱“異常點”的作用。當背景諧波波動時，穩健回歸具有明顯優勢。其優化的目標函數為：

(5)

采用式(6)所示bisquare法定義權重：

(6)

式中c為常量，一般取4.685；ui為標準化的殘差指標；s為殘差尺度。

ui=ei/s

(7)

s=MAD(e1,…,en)/0.6745

(8)

MAD(e1,…,en)=Median|e1-Median(e1,…,en)|

(9)

這里，Median為變量的中位數。

穩健回歸具體步驟如下：

(2)利用式(11)和式(12)計算標準化殘差u，將其帶入式(10)中，并化為對角線權向量W；

2.4 諧波阻抗估算流程

提出的諧波阻抗估算方法流程圖如圖3所示。

在諧波阻抗估算中，首先采用DBSCAN聚類將諧波阻抗相同的數據組篩選到一起，再對每個組根據式(3)和式(4)進行復相關性分析，篩選出背景諧波電壓較穩定的數據段，最后估算系統阻抗值。

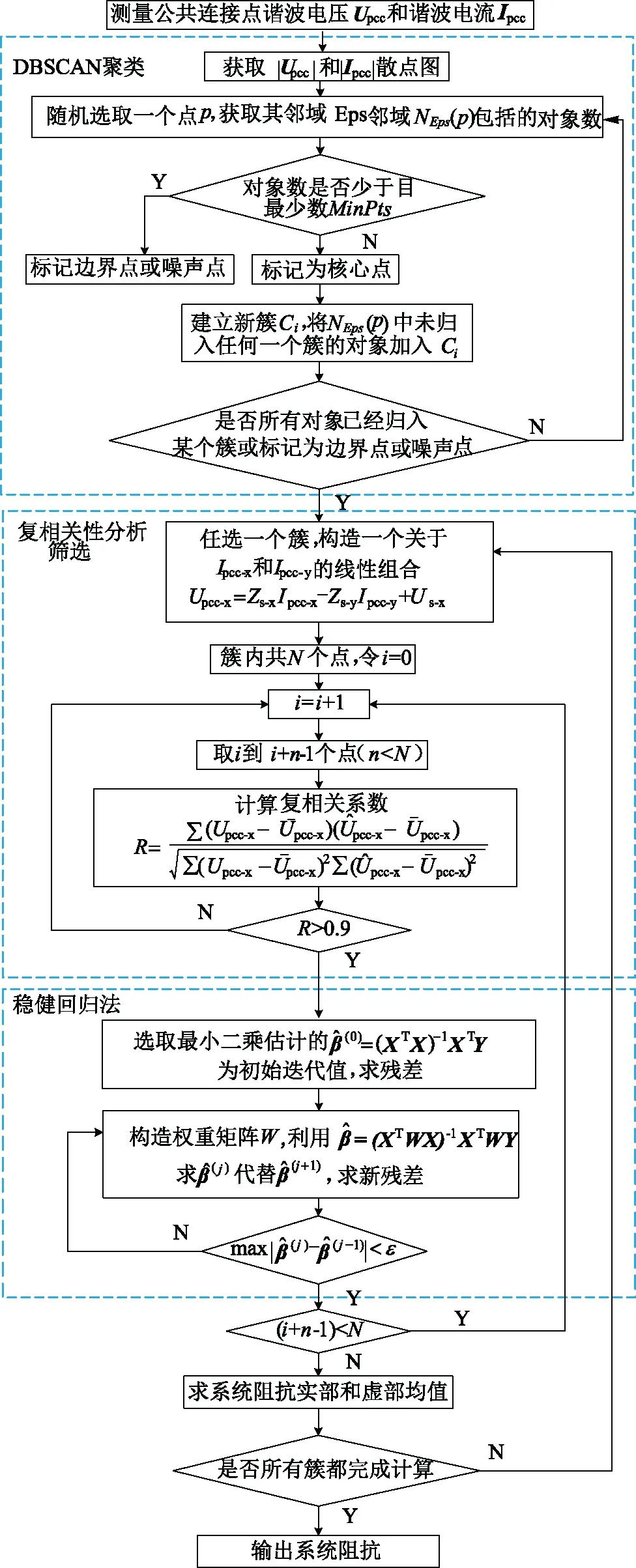
圖3 諧波阻抗估算流程Fig.3 Flow chart of harmonic impedance estimation

3 實驗結果與分析

搭建如圖1所示的等效電路圖，以5次諧波為例，設定用戶側5次諧波等效阻抗值為150+j 200 Ω，用戶側等效電流源諧波發射均值3+j2 A；系統側阻抗t0時刻為1+j2 Ω，t1時刻變化到4+j3 Ω，在t2時刻變化到5+j4 Ω，系統側諧波電壓均值分別為2+j3 V，在諧波源中加入大小不等的波動，仿真共取800個樣本點，t0、t1和t2分別對應樣本點0、 400和600。

3.1 系統阻抗改變點辨識

將所提出的DBSCAN辨識系統阻抗變化方法與文獻[18]提出的小波辨識法(方法1)和文獻[19]提出的斜率辨識法(方法2)作對比。

對于方法1，根據文獻[18]，測量PCC處5次諧波電壓和諧波電流矢量值，計算系統阻抗粗估值見圖4。

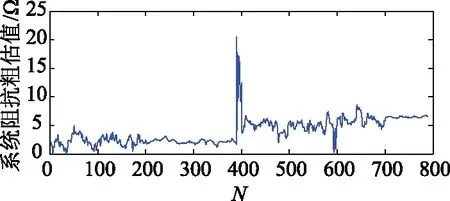
圖4 系統阻抗粗估值Fig.4 Rough estimation of system impedance

再對系統阻抗粗估值做小波變換，提取高頻分量d1和d2的波形如圖5所示。

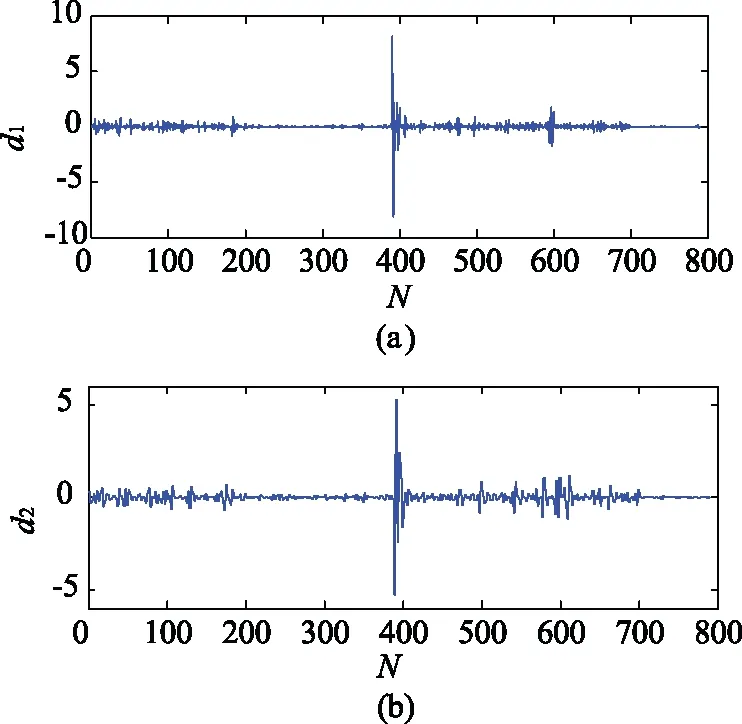
圖5 高頻分量Fig.5 High frequency component

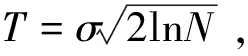
計算高頻分量d1中突變點為391、 393和397，d2中突變點為391、 392、 395和396，這與設定的400和600這兩個突變點不相符，其原因在于t2時刻突變前后系統阻抗值變化較小，且背景諧波電壓波動的干擾較大，因而方法1失效。

對于方法2，根據文獻[19]，獲得以|Ipcc|為橫坐標、|Upcc|為縱坐標的散點圖如圖6所示，計算圖6中每相鄰兩點之間的斜率值，如圖7所示。

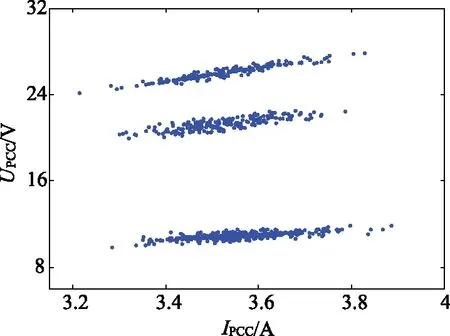
圖6 散點圖Fig.6 Scatter plot

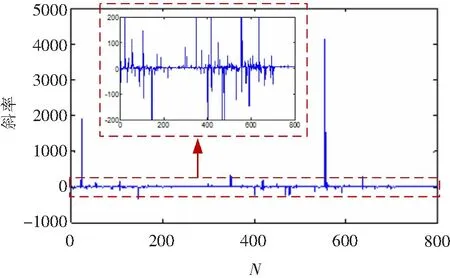
圖7 斜率值Fig.7 Slope value

由于斜率和系統阻抗值有關，故文獻[19]通過對斜率設定閾值，將不同斜率(系統阻抗)對應的數據點分開。但如圖7所示，由于背景諧波電壓波動的干擾，導致斜率值波動較劇烈，無法通過斜率正確辨識系統阻抗真實值，故方法2失效。

由圖6可以看到散點圖呈3個長條狀分布，分別對應3個可能的阻抗值，采用文中方法提出方法(DBSCAN法)對散點圖進行聚類分析，獲得聚類效果對比見圖8。

由圖8可知，所提出的DBSCAN法能將圖6中的3簇數據正確分開，這與仿真設置的2次阻抗變化點相對應。為了驗證提出方法的有效性，并在DBSCAN聚類的基礎上做進一步系統阻抗估算實驗。

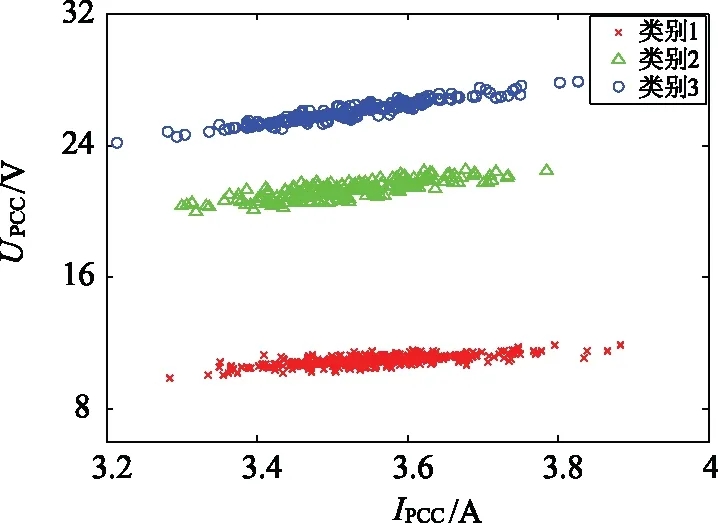
圖8 DBSCAN聚類結果Fig.8 DBSCAN clustering results

3.2 系統阻抗估算

對DBSCAN聚類后的數據分別采用波動量法(方法3)、偏最小二乘法(方法4)計算系統阻抗值，并對DBSCAN聚類后的數據進行復相關性分析，篩選出系數高于0.9的數據段，再用穩健回歸法估算系統阻抗值(方法5/文中方法)。計算結果如表1所示，并計算相對誤差如表2所示。

表1 諧波阻抗估算結果Tab.1 Estimation results of harmonic impedance

表2 諧波阻抗估算誤差Tab.2 Estimation error of harmonic impedance

由表2可知，方法5(文中方法)估計系統阻抗值的誤差最小，驗證了所提出的DBSCAN聚類、復相關性分析篩選和基于bisquare權重的穩健回歸法估計系統阻抗方法的有效性。

4 結束語

文章綜合考慮了系統阻抗變化和背景諧波電壓波動的情況，提出諧波阻抗估算新方法。對諧波電壓和諧波電流的散點圖進行DBSCAN聚類分析，將不同諧波阻抗對應的數據組分離，進行復相關性分析，篩選出背景諧波電壓較穩定的數據段，采用基于bisquare權重的穩健回歸法進行系統阻抗估算。仿真表明，當系統阻抗變化時，所提出的DBSCAN聚類方法能有效分離系統阻抗恒定的數據段，所提出復相關性分析篩選法和基于bisquare權重的穩健回歸法能進一步提高系統阻抗估計的精度，提出方法適用條件更廣，有一定的應用價值。