RV減速器擺線輪組合修形及優化

張哲衍, 柳 麗*, 羅利敏, 李國平, 莫緒倫

RV減速器擺線輪組合修形及優化

張哲衍1, 柳 麗1*, 羅利敏2, 李國平1, 莫緒倫2

（1.寧波大學 浙江省零件軋制成形技術研究重點實驗室, 浙江 寧波 315211; 2.寧波中大力德智能傳動股份有限公司, 浙江 寧波 315301）

為提高RV減速器的傳動性能, 本文針對擺線輪齒廓的工作區域及組合修形方法等展開研究. 對應用廣泛的“等距+移距”修形進行組合比較, 確定“正等距+負移距”的組合方式下初始間隙最小, 即嚙合剛度最高; 分析針齒與擺線輪嚙合的極限位置, 推導擺線輪的實際工作區域, 并對其采用遺傳算法尋找最優修形量, 使組合修形逼近轉角修形所得齒廓. 結果顯示, 該方法得到的擺線輪齒廓在工作區域內更接近共軛齒廓, 且在齒頂與齒根處有合適的徑向間隙, 可在提高擺線輪強度的同時有效補償制造誤差和安裝誤差, 對擺線輪的修形方式選擇及修形量確定具有一定的借鑒意義.

擺線輪; 工作區域; 組合修形; 遺傳算法; 誤差補償

RV減速器是在擺線針輪傳動基礎上開發的一種高精密傳動裝置, 具有傳動比大、結構緊湊、運動精度高、剛度大、磁滯誤差小和傳動效率高的優點[1], 廣泛應用于工業機器人、航空航天等領域[2]. 擺線輪作為RV減速器的關鍵傳動部件, 其齒形輪廓直接影響傳動精度、效率、壽命等重要性能[3]. 故研究擺線輪的最佳修形方法及修形量具有重要的現實意義.

李力行[4]闡述了擺線輪齒廓修形的3種基本方式, 即等距、移距以及轉角修形. Wang等[5]通過比較不同修形組合下的初始嚙合間隙大小, 探尋嚙合剛度最高的組合. 于影等[6]通過分析針齒嚙合的兩個極限位置, 推導出擺線輪與針齒嚙合的實際工作范圍. Ren等[7]提出一種通過關鍵點來定義擺線輪修形齒廓的修形方法, 并通過數值實驗驗證了該方法能有效提高擺線針輪傳動的承載能力. Li等[8]在修形過程中考慮壓力角的影響, 提出一種新的齒廓修形數學模型.

本文綜合3種基本齒廓修形方式的優點, 在擺線輪嚙合剛度最大的修形組合下使實際工作區域內“等距+移距”修形所得齒廓逼近轉角修形所得齒廓. 采用遺傳算法對該區域齒廓直接尋優, 提高了優化效果. 通過對某企業RV20E-ASSY-81i型減速器擺線輪的優化, 驗證了該方法的實用性.

1 擺線輪組合修形

1.1 擺線輪齒廓方程

與針齒共軛且無嚙合間隙的擺線輪齒廓稱為標準齒廓[9]. 實際應用中, 為補償制造誤差并確保良好的潤滑, 必須對擺線輪輪廓進行修形. 根據擺線輪嚙合及成形機理, 有如圖1所示的擺線輪齒形曲線.

圖1 擺線輪齒形曲線

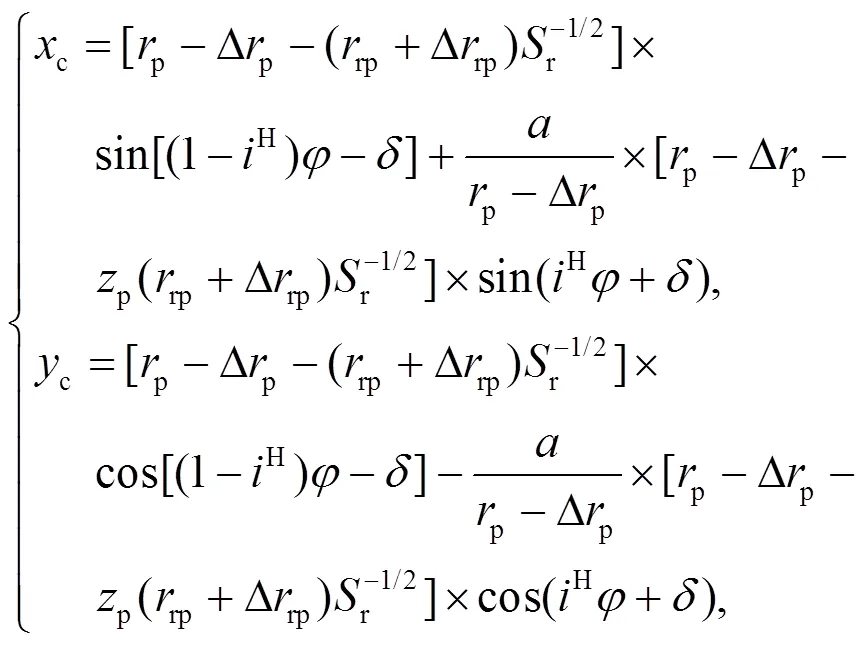
1.2 不同修形方式的初始間隙

上述3種修形方法中, 轉角修形所獲得的擺線輪齒廓屬于共軛齒廓, 可保證傳動的平穩性, 但其磨出的擺線輪在齒頂和齒根處無法產生間隙, 故不能單獨使用. 而等距修形與移距修形磨削工藝簡單, 且可根據具體要求獲得合適的徑向間隙, 故在實際應用中多采用等距、移距或其組合的方式進行齒廓修形.

擺線輪經等距、移距修形后會在其理論嚙合點(標準擺線輪與針齒的嚙合點)的法線方向產生初始間隙. 初始間隙的大小影響擺線輪與針齒的嚙合對數, 從而影響其嚙合剛度. 現分析不同修形方式的初始間隙.

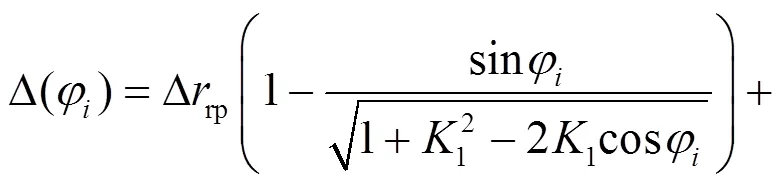
以某企業RV20E-ASSY-81i型減速器的擺線輪為例, 其基本參數見表1.

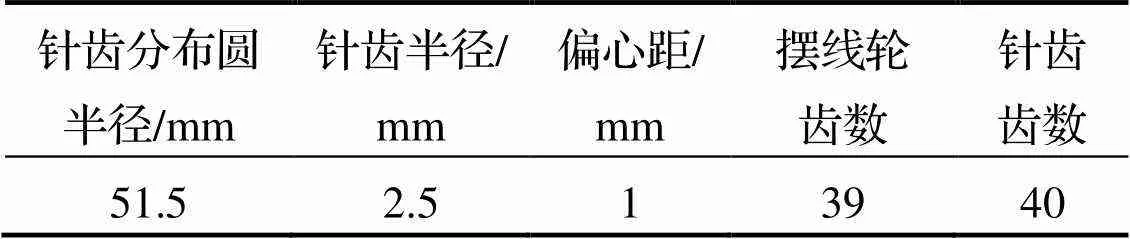
表1 RV20E-ASSY-81i型減速器擺線輪基本參數

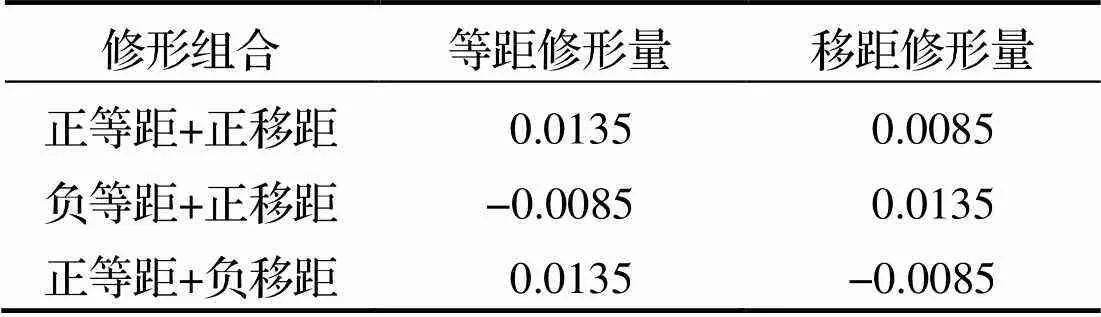
表2 不同修形組合的修形量 mm

圖2 不同修形組合下的初始間隙

由圖2可知, 相比其他修形方式,“正等距+負移距”的修形組合可獲得更小的初始嚙合間隙. 更小的初始間隙不但更接近標準齒形曲線, 還可使修形后的擺線輪與針齒的嚙合對數增加, 提高嚙合剛度. 因此, 本文選擇“正等距+負移距”的組合進行擺線輪修形.

2 擺線輪工作區域

在擺線輪的工作過程中, 并非所有齒廓都參與嚙合, 因此在擺線輪齒廓修形優化之前, 需確定其工作區間, 從而確保優化結果的可靠性.

2.1 擺線輪工作區域分析

圖3 擺線輪工作區域

已知:

由定比分點定理可得:

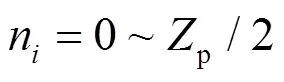
2.2 擺線輪工作區域確定

將RV20E-ASSY-81i型減速器擺線輪基本參數代入公式(3), 通過Matlab計算可得如圖4所示的針齒嚙合相位角函數曲線.

圖4 嚙合相位角函數曲線

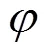
則該擺線輪的工作區域為

3 擺線輪的修形及優化

為使擺線輪齒廓的工作區域能最大限度逼近共軛齒形, 且在齒頂齒底產生徑向間隙, 選擇等距、移距組合修形逼近轉角修形的優化方法, 結合前文研究, 組合形式為“正等距+負移距”.

3.1 設計變量及目標函數

3.2 約束條件

3.3 遺傳算法尋優

選擇遺傳算法對目標函數(4)進行尋優, 參數設置如下: 給定初始種群數目num=20, 迭代40次. 最小適應度收斂曲線如圖5所示.

圖5 組合修形優化最小適應度收斂曲線

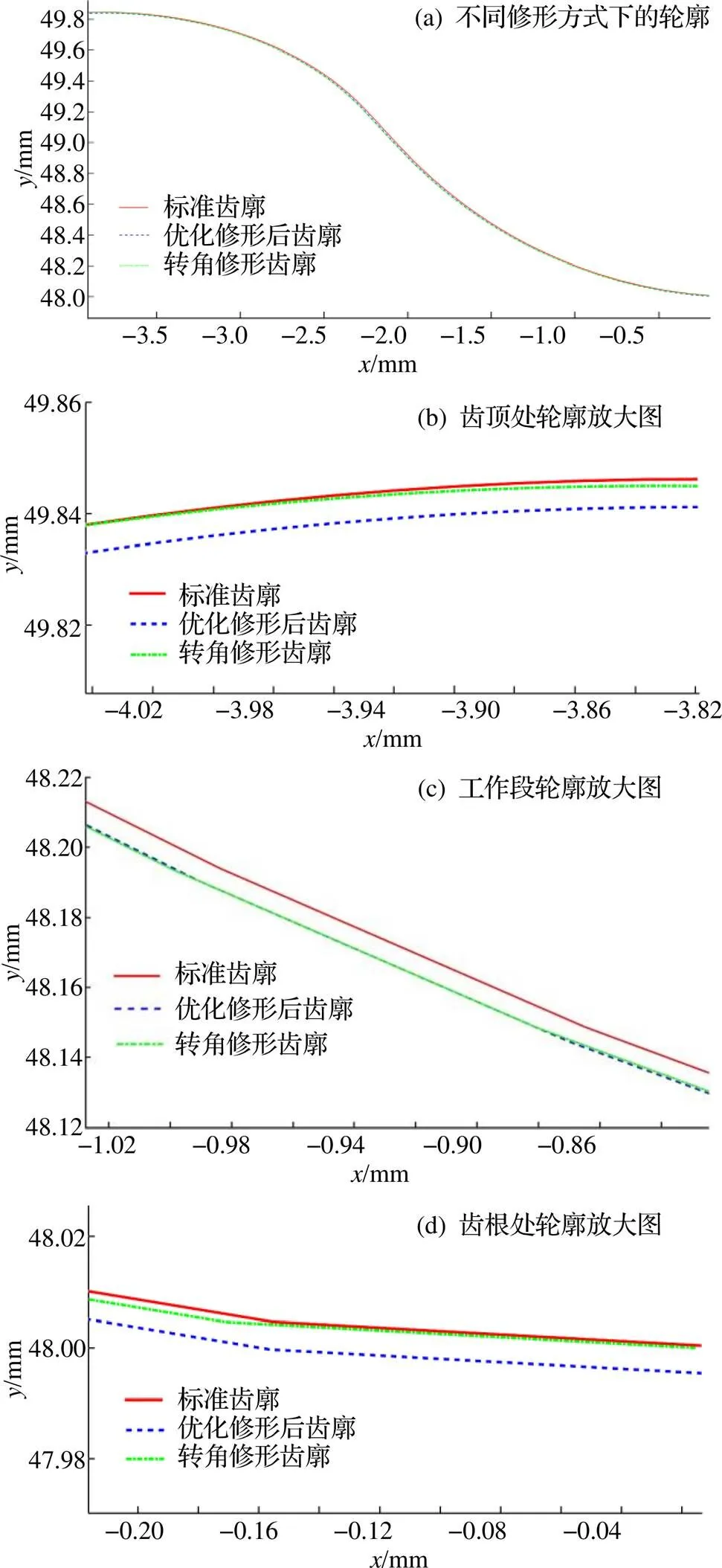
圖6 擺線輪輪廓曲線

4 結論

為獲得加工工藝簡便、嚙合剛度大、傳動性能好的擺線輪齒廓, 本文做了以下研究:

(1)比較不同組合方式下擺線輪與針齒初始間隙的大小, 獲得在“正等距+負移距”組合修形方式下擺線輪嚙合間隙最小、嚙合剛度最大的結論.

(2)推導了擺線輪工作區域的嚙合相位角數學公式, 并確定工作區域大小.

(3)用“正等距+負移距”的組合修形方法來逼近轉角修形的齒廓, 采用遺傳算法對優化問題求解. 優化后的齒廓在工作區域更接近共軛齒廓, 且能在齒頂與齒底形成合適的徑向間隙, 有效補償制造誤差及安裝誤差, 留下足夠的潤滑空間.

[1] 李力行, 何衛東, 王秀琦, 等. 機器人用高精度RV傳動的研究[J]. 大連鐵道學院學報, 1999, 20(2):1-11.

[2] 汪泉, 曾利磊, 秦爭爭. 考慮擺線輪齒廓修形的RV減速器齒輪結構多目標優化設計[J]. 機械傳動, 2020, 44 (4):54-60.

[3] 魏波, 周廣武, 楊榮松, 等. RV減速器擺線輪齒廓修形方法對比研究[J]. 機械設計與研究, 2016, 32(1):41- 44; 47.

[4] 李力行. 擺線針輪行星傳動的齒形修正及受力分析[J]. 大連鐵道學院學報, 1984, 5(4):29-40.

[5] Wang J, Gu J, Yan Y. Study on the relationship between the stiffness of RV reducer and the profile modification method of cycloid-pin wheel[C]//International Conference on Intelligent Robotics & Applications, 2016:721-735.

[6] 于影, 邵忠喜, 于波. 擺線輪嚙合齒形工作范圍的確定[J]. 機械設計與研究, 2006, 22(5):65-67.

[7] Ren Z Y, Mao S M, Guo W C, et al. Tooth modification and dynamic performance of the cycloidal drive[J]. Mechanical Systems and Signal Processing, 2017, 85: 857-866.

[8] Li T X, An X T, Deng X Z, et al. A new tooth profile modification method of cycloidal gears in precision reducers for robots[J]. Applied Sciences, 2020, 10(4):1266.

[9] 徐宏海, 馮玉賓, 劉學翱, 等. RV傳動嚙合齒形參數化設計及其軟件開發[J]. 現代制造工程, 2015(1):125- 128.

[10] 程乃士. 減速器和變速器設計與選用手冊[M]. 北京: 機械工業出版社, 2007.

[11] 丁國龍, 秦園, 明廷伯, 等. 基于接觸應力均化的擺線輪修形方法[J]. 中國機械工程, 2019, 30(9):1081-1089.

[12] 曾德強. RV減速器擺線輪修形設計與優化[D]. 北京: 中國石油大學(北京), 2019.

[13] 秦爭爭, 汪泉, 趙大興, 等. 補償彈性變形的擺線輪齒廓修形方法[J]. 機械強度, 2020, 42(3):661-666.

Combined modification and optimization of cycloid wheel of RV reducer

ZHANG Zheyan1, LIU Li1*, LUO Limin2, LI Guoping1, MO Xulun2

( 1.Zhejiang Provincial Key Laboratory of Part Rolling Technology, Ningbo University, Ningbo 315211, China; 2.Ningbo Zhongda Leader Intelligent Transmission Co., Ltd., Ningbo 315301, China )

In order to improve the transmission performance of RV reducer, the working area of cycloid tooth profile and the combined modification method are studied in this paper. By comparing the widely used modification of “equal distance + displacement”, it is found that the initial clearance under the combination of “positive equal distance + negative displacement” is the smallest, i.e., the meshing stiffness is the highest. The limit position of the meshing between the pin tooth and the cycloid gear is analyzed, the actual working area of the cycloid gear is deduced, and the genetic algorithm is used to find the optimal modification value, so that the combined modification can approach the tooth profile obtained by the angle modification. The results show that the cycloid tooth profile obtained by this method is closer to the conjugate tooth profile in the working area, and there is an appropriate radial clearance between the tooth top and the tooth root, which can effectively compensate both the manufacturing error and the assembly error while at the same time improving the strength of the cycloid gear. It has certain reference significance for the selection of cycloid gear’s modification mode and the determination of the optimal modification value.

cycloidal wheel; working area; combined modification; genetic algorithm; error compensation

TH132

A

1001-5132（2022）01-0063-05

2021?06?07.

寧波大學學報（理工版）網址: http://journallg.nbu.edu.cn/

寧波市“科技創新2025”重大專項（2018B10007, 2019B10078, 2018B10005）.

張哲衍（1995－）, 男, 浙江慈溪人, 在讀碩士研究生, 主要研究方向: 結構優化設計. E-mail: zhangzheyan1011@163.com

柳麗（1968－）, 女, 甘肅民勤人, 副教授, 主要研究方向: 機構設計與分析等. E-mail: liuli@nbu.edu.cn

（責任編輯 韓 超）