數字圖像處理技術在獲取表面分形維數中的應用
李 鑫
(奇瑞汽車股份有限公司,安徽 蕪湖,241000)
為了研究表面形貌對摩擦學的影響,Archard[1]提出了多尺度接觸模型,將表面微凸體視作大小不等的半球體,通過給定半球體在表面上的分布密度構造表面形貌,但是,分布密度往往不能直接測量獲得,所以,對表面構造存在一定的假設成分。Majumdar等[2]提出了基于接觸表面分形幾何的接觸理論,接觸面表面形貌用Weierstrass[3]提出的分形函數模擬,分形函數中的特征參數可通過測量手段獲得,這樣就作到了表面形貌模型與實際的統一,排除了對表面形貌的假設成分。
分形理論應用于生活中的許多領域[4],分形維數是表面分形幾何中的重要參數,它的大小直接反映了表面的粗糙情況[5~9]。通常,如果獲得表面形貌輪廓曲線,可通過尺碼法獲得分形維數[10~13]。但是,實際測得的分形表面輪廓曲線往往致密繁亂,而尺碼法是通過操作員利用尺規作圖的方法進行測量,致密的輪廓曲線在很大程度上會影響操作員對曲線的辨識[14~16],導致測量結果隨機性大,直接影響其它涉及表面形貌的相關估算。
為了減少人為因素對表面形貌參數獲取過程的影響,筆者在此提出利用數字圖像處理技術對表面分形維數的獲取方法。該方法利用尺碼法測量分形維數的原理,對表面輪廓曲線進行二值化處理,并給出基于邏輯像素的尋點算法,最終展示了利用數字圖像處理技術獲取分形維數的實現流程。
1 分形表面形貌
分形的概念首先得到了Benoit B. Mandelbrot的印證[2]。起初,Benoit B. Mandelbrot通過測量地圖上的海岸線長度發現,以不同的長度作為標尺丈量海岸線的長度,其結果是不同的,當選擇的尺度越小,海岸線的細節特征(例如港口等)就會顯現的越多,測量所得的海岸線長度就越準確。分形表面也具有類似的特征,當觀察一個表面的形貌時,如果選擇的觀察尺度不同,所觀察到的細節特征也不相同。譬如,當在一個尺度下觀察到分形表面上的微凸體時,如果增大放大倍數重新觀察該微凸體,就會發現,該微凸體內分布著許多更小的微凸體(圖1)。
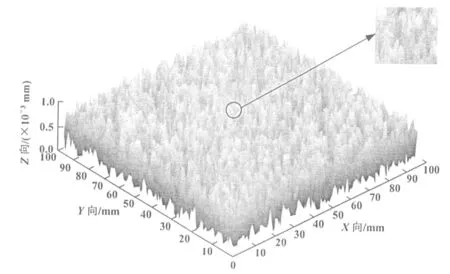
圖1 分形表面計算機模擬
Weierstrass[3]指出,具有分形特征的表面輪廓曲線可以用下列函數表示:
(1)
其中:G為特征尺度系數,D為分形維數,其范圍是1 圖2 分形表面輪廓曲線 Weierstrass[3]通過研究發現,雖然在不同尺度下觀察到的表面形貌不同,但是不同尺度下的表面形貌具有自相似性,即均可以通過統一的參數來表征不同尺度下的形貌,也就是說,分形表面具有尺度獨立性,而分形維數就是具有尺度獨立性的形貌特征參數。 仿照Benoit B. Mandelbrot對海岸線長度的測量方法,可以選用不同的長度尺度ri對表面輪廓曲線長度Li進行測量(圖3),根據分形理論,長度與尺度之間的關系可以表示為: 圖3 尺碼法確定分形維數示意圖 圖4 表面輪廓曲線圖像二值化處理 (2) 其中:k為比例系數,α為特征指數。 對上式取對數得: lnLi=αlnri+lnk (3) 可見,lnLi與lnri之間呈線性變化關系,如果在坐標系擬合出lnLi-lnri直線,即可得出直線斜率α,而α與分形維數D的關系是: D=1-α (4) 那么,就能根據擬合結果求出分形維數D。 通過將圖2所示的輪廓曲線讀入計算機發現,該圖像在計算機中的表示是一個大型二維數組,數組中的元素是0~255范圍內的數值(圖像默認存儲為RGB色系),有輪廓曲線的像素數值偏低,背景的像素數值偏高,盡管輪廓曲線和背景的像素數值分化明顯,但是每一部分的像素數值并不統一,輪廓曲線的像素數值相對集中在0~15區間內,背景的像素數值相對集中在230~255區間內。為了接下來使圖像處理技術能在尺碼法中得到應用,需要將輪廓曲線從背景中剝離出來,而且還需保證輪廓曲線的像素數值統一。于是,先對圖像進行二值化處理,以RGB色系的中間數作為閾值,對圖像進行判斷,凡低于閾值的像素均設為邏輯0,高于閾值的像素均設為邏輯1。這樣,一幅RGB色系的圖像便被轉化為僅由0和1組成的邏輯像素圖像,輪廓曲線也都被統一成一個邏輯像素值0(圖4)。 如果將邏輯像素圖像局部放大,其中黑色像素代表邏輯值為0的輪廓曲線,白色像素代表邏輯值為1的背景。用A表示二值化圖像后的數組,給定尺碼尺度r,可仿照如下流程對滿足尺碼尺度的輪廓曲線像素點進行尋找(圖5): 圖5 圖像處理技術提取分形維數示意圖 從輪廓曲線上某一個像素(i,j)向右出發((i,j)為像素坐標,i代表第i列,j代表第j行),搜索第i+1列,從(i+1,j)開始向上搜索至(i+1,1),如果發現邏輯值為0的像素(假設其坐標為(x,y)),然后進行判斷;如果未發現邏輯值為0的像素,則開始向下搜索至(i+1,size(A(:,1))),然后進行判斷。判斷的條件是:(x-i)2+(y-j)2>r2?如果判斷結果為真,則存儲當前像素坐標,并將其作為新的起點開始下一輪搜索;如果判斷結果為假,則開始搜索第i+2列,搜索方法同上,直至到第i+r列。輪廓曲線的長度即可表示為: (5) 其中,N代表搜索到的符合條件的節點個數。 通過上面的介紹,能夠得到圖像處理技術獲取分形維數的方法(圖6)。首先,將圖像做二值化處理,得到圖像的邏輯像素數組,輸入尺碼r的值和初始節點的坐標值(i,j),然后按照指定的搜索方向尋找下一個滿足要求的節點。其中,滿足要求是指要滿足2個條件:(1)能夠找到邏輯像素為0的節點;(2)到(i,j)節點距離滿足(x-i)2+(y-j)2>r2的條件。如果找到這樣的節點,則保存其坐標,并作為下一輪搜索的起始坐標;如果沒找到這樣的節點,則代表對輪廓曲線的長度測量工作已完成,那么輸出輪廓曲線長度的測量結果(式(5)),同時存儲此次測量的點對(L,r)。 圖6 圖像處理技術提取分形維數的流程 通常情況下,得到的分形表面輪廓曲線長度都較長,采用上述過程測量輪廓曲線長度的計算量較大。然而,根據分形理論,分形參數是具有尺度獨立性的,所以,為減小計算量,可截取實際輪廓曲線的一部分進行上述計算過程。 筆者開發了“數字圖像處理技術獲取分形維數”的計算界面(圖7),界面包含初始節點坐標輸入、尺碼輸入,還包括擬合點對數量輸出、擬合分形維數輸出、原始圖像和擬合曲線顯示。“提交”按鈕根據輸入的初始節點坐標和尺碼執行一次計算過程,并記錄該次結果:(L,r)。同時,“點對數量”從零開始,每點擊1次“提交”按鈕就自動加1。“擬合”按鈕將“提交”按鈕存儲的點對進行雙對數線性擬合,得到的斜率按照式(4)計算得出分形維數,在“分形維數”項后顯示。 圖7 圖像處理技術提取分形維數的算例界面 本節首先根據已知的分形維數,按照式(1)在計算機上得到分形表面輪廓曲線,然后將其保存為圖片,再讀入到計算界面,通過相關計算得到擬合的分形維數,與已知的分形維數進行比較(表1)。 對比結果表明,利用圖像處理技術提取分形維數能夠得到較準確的結果,一般誤差都在10%左右。但是,隨著擬合點對數量的增加,所得到的擬合結果也越來越趨近于真實結果,誤差在10%以內。如果有足夠多的點對進行擬合,誤差會更小。 利用粗糙表面輪廓曲線的功率譜密度表征表面粗糙程度的方法稱為功率譜方法,該方法的提出解決了具有相同粗糙度值,但是卻明顯不同的兩個表面形貌表征問題。《摩擦學的分形》[5]中作者展示了功率譜法測量分形維數的方法,通過對不同分形維數采用功率譜法和基于圖像處理的提取法得到的誤差分布可以發現,對于有些分形維數,功率譜法可能會獲得更理想的測量結果(圖8)。但是,功率譜法的測量結果變化范圍較寬,測量穩定性稍顯波動;相反地,如果選擇足夠多的測量點對,利用基于圖像處理技術的分形維數提取法可以獲得較穩定的測量結果,而且誤差范圍也在可接受的范圍內。 圖8 功率譜法和基于圖像處理的提取法測量結果對比 筆者提出的基于圖像處理的分形維數提取方法能夠獲得準確度范圍可接受的分形維數測量結果。隨著準確度的提升,需要采集的點對數量也會增加,在算法中所進行的計算量也會相應增加(計算量主要來源于對像素點的搜索和距離判斷)。計算結果表明,點對數不需要采集過多即可獲得滿足工程精度需要的分形維數(表1),所以筆者提出的基于圖像處理的分形維數提取方法并不需要占用太多的計算機資源。 表1 不同分形維數提取結果比較 本次研究提出了利用數字圖像處理技術對表面分形維數的獲取方法。該方法利用尺碼法測量分形維數的原理,對表面輪廓曲線進行二值化處理,并給出基于邏輯像素的尋點算法,最終展示了利用數字圖像處理技術獲取分形維數的實現流程。結果表明,利用圖像處理技術,可以保證獲取分形維數的準確度在10%左右的誤差范圍內,而且隨著擬合點數量的增加,準確度增加。通過比較發現,基于圖像處理的分形維數提取方法具有較好的測量穩定性,而且無需占用太多的計算機資源即可獲得較高精度。該方法的提出,能夠很大程度上減少人為因素對獲取分形維數的影響。 致謝:本研究成果感謝“安徽高校自然科學研究重點項目”(編號:KJ2020A0359)和“安徽高校協同創新項目”(編號:GXXT-2019-048)的支持。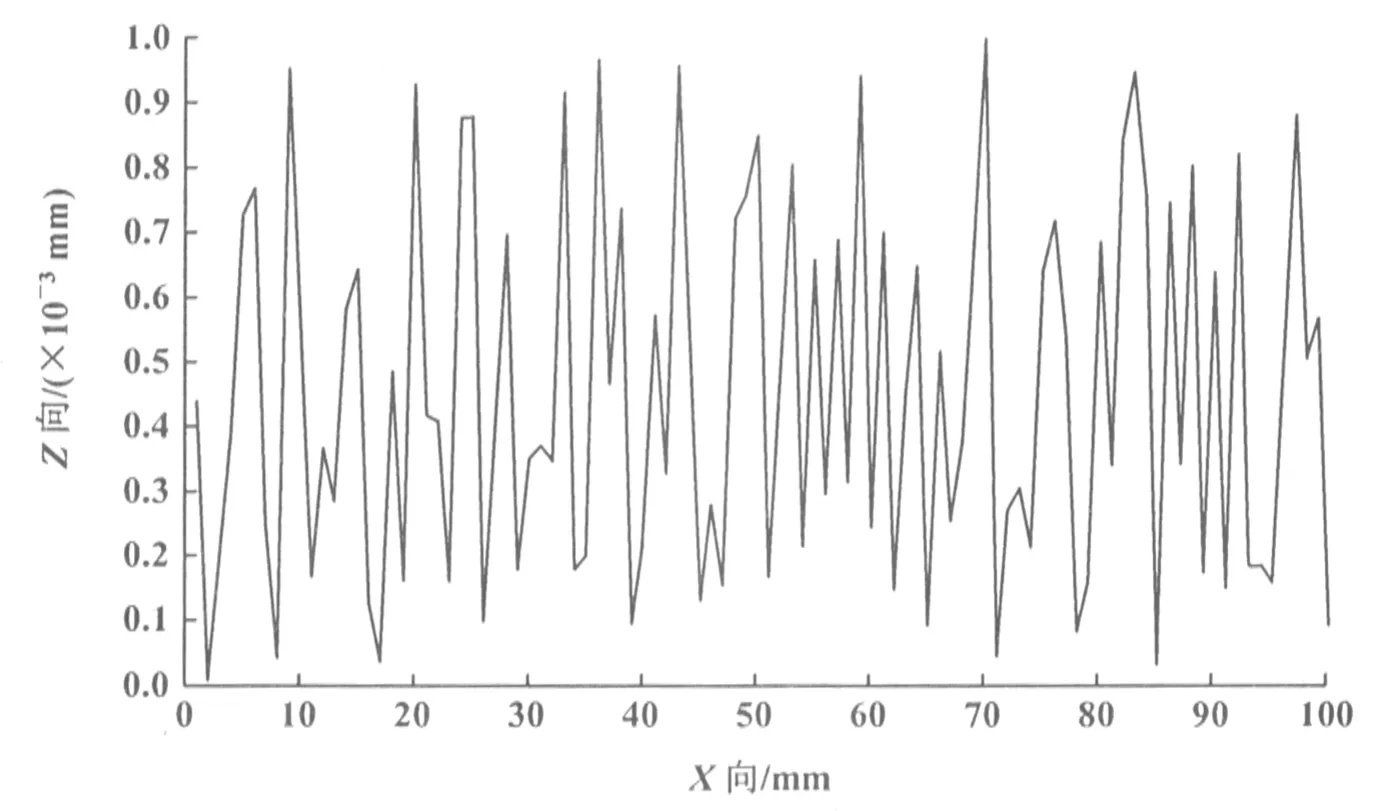
2 分形維數的提取
2.1 尺碼法提取分形維數
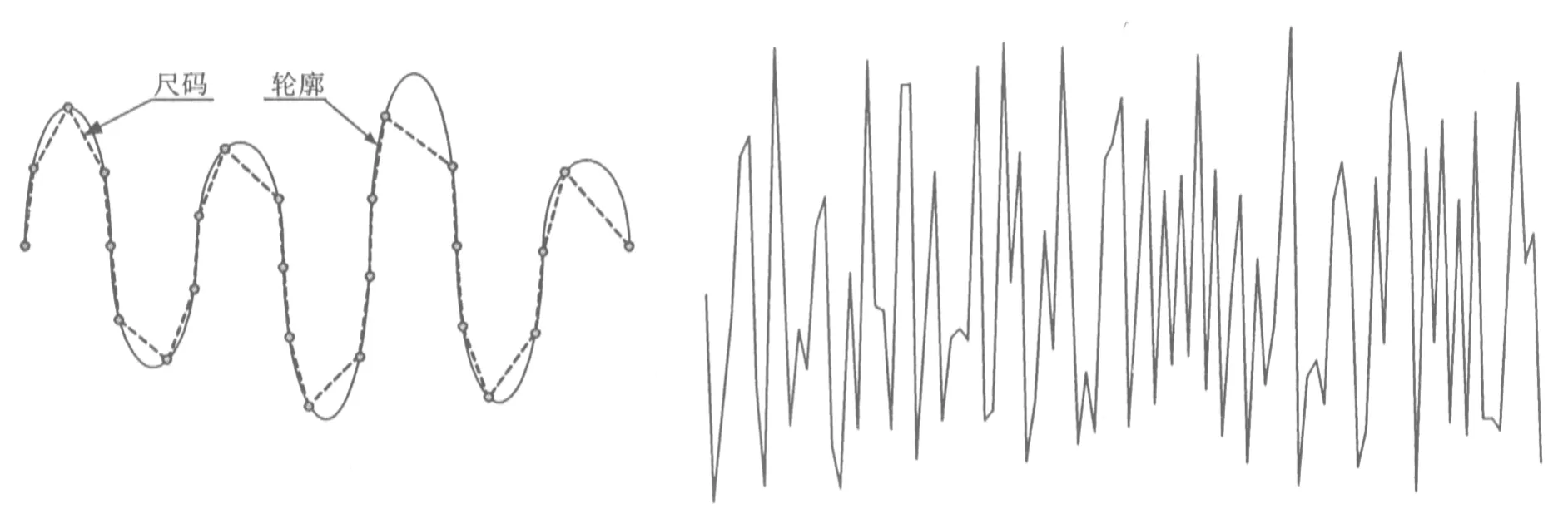
2.2 數字圖像處理在尺碼法中的應用
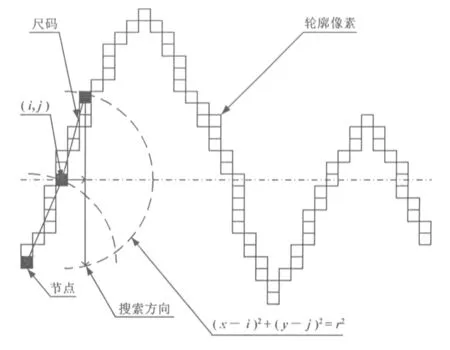
2.3 數字圖像處理對分形維數的提取方法
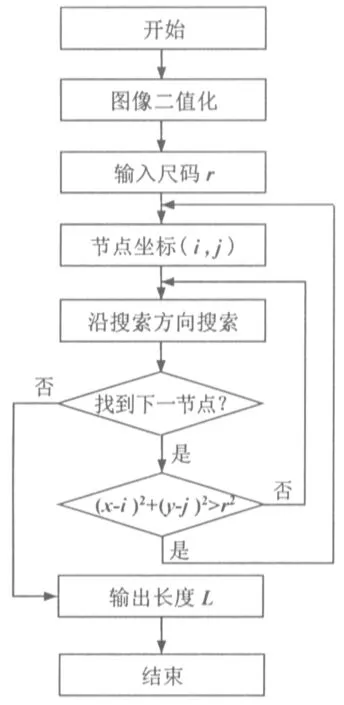
3 結果與分析

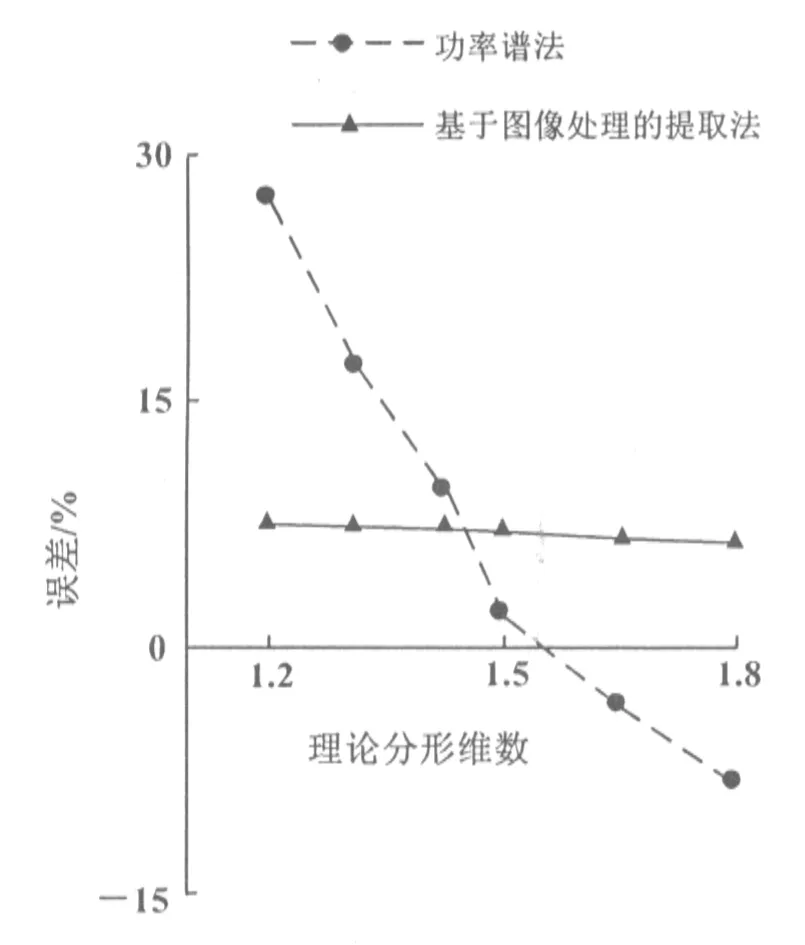

4 結論與討論

