量子計算模擬及優化方法綜述

喻志超，李揚中，劉 磊，2，馮圣中

（1.國家超級計算深圳中心（深圳云計算中心），廣東深圳 518055；2.中國科學院計算技術研究所計算機體系結構國家重點實驗室，北京 100190）

0 概述

量子計算是一種遵循量子力學規律調控量子信息單元進行計算的新型計算方式。由于量子力學疊加態的存在，量子計算機與經典計算機相比具有更強大的并行信息處理能力，并有望解決經典計算機無法解決的問題。量子計算被認可的潛在應用領域包括密碼學［1］、量子化學［2］、材料科學［3］、機器學習［4］等。

研究量子計算技術，需要開展精確的量子門操作和糾錯、容錯等實驗，以及模擬量子疊加、糾纏等狀態，構造足夠復雜的相干量子計算實驗體系，并開展適用的量子計算模型和算法研究。量子計算的主要研究方向包括構造含有更多量子比特的通用量子計算機、設計更有效的量子算法以及優化量子程序編譯器［5-6］，從而使得量子計算機能被廣泛使用。現階段的量子計算機屬于嘈雜的中尺度量子（Noisy Intermediate Scale Quantum，NISQ）計算機［7-8］，量子位的數量尚不過百，量子位狀態脆弱且易受干擾，無法保證量子程序的可靠執行，也無法適用于求解大規模的科學計算問題。自從谷歌提出量子優越性以來，如何展示現階段量子對于經典計算機的優勢一直是研究熱點［9-11］。由于量子比特受到噪聲的影響易失去量子特性，而基于量子糾錯碼的容錯架構可能是利用量子計算機執行大規模計算的重要基礎，因此設計一種使用適度資源即能有效對抗實際噪聲的實用量子糾錯碼，也是量子計算核心問題之一［12-13］。此外，探索新的效率明顯優于經典計算機算法的量子算法，也已經成為量子計算理論研究的一個重要分支［14］。

由于已知量子運行規律，因此可使用經典計算機模擬量子計算。量子計算模擬器相比于物理量子比特計算機的突出優勢是功能齊全，可執行的量子程序規模不會受到物理量子計算機保真度的制約，是理想的量子算法測試平臺［15］。量子計算模擬包括計算并存儲所有量子態、部分或者單個量子態概率幅、含噪聲模擬等多種形式，不同的模擬方法對應于不同的量子計算目標。許多研究機構開發了量子線路模擬器用來支撐量子計算領域復雜問題的模擬，如太章模擬器［10-11］、ProjectQ［16］、qHiPSTER［17］、QuEST［18］等。量子模擬器可被部署于分布式超級計算機集群，利用超算集群的運算性能實現量子計算的高效模擬，模擬過程中需要考慮子任務劃分和通信優化問題，通過分布式節點上任務的合理分配和減少通信成本的設計策略，實現均衡分布式節點間負載的目標。

為了能夠模擬具有更多量子比特數且深度更深的量子線路，如何減少模擬所需存儲和提高模擬計算效率是關鍵問題。現有研究對算法的優化改進，使得模擬器在實際應用中已經取得了較大突破。針對目前量子計算模擬的研究工作，本文綜述實現量子計算模擬的基本方法，總結量子線路模擬的優化方法和已有的模擬器，并闡述在超算上模擬量子計算的核心問題，討論相應的優化方法。

1 量子計算原理

本節主要介紹量子計算理論中的背景知識，包括量子比特、量子門、量子線路、量子操作系統和量子模擬。

1.1 量子比特

經典計算機的比特位只有0 和1 兩種狀態，而量子比特中這樣確定的狀態則被稱為基本態，除此之外，還有可能是2 種狀態的疊加態。一個量子比特位（量子位）的狀態（狀態向量表示）可以看作是由兩個基本態（計算基態向量和）組成的二維復空間向量。根據量子規律，單量子比特可以是兩種基本態疊加成的任一種狀態，用狀態向量公式表示為：

其中，系數α、β為復數值的概率幅，|α|2和|β|2分別為對應狀態的概率且滿足|α|2+|β|2=1。

n位量子比特的狀態向量可以表示為2n個基態的復合態：

1.2 量子門

經典計算使用邏輯門操作經典比特的狀態，量子計算則使用量子門操作量子位狀態。量子態滿足歸一約束|α|2+|β|2=1，經過量子門作用后得到的量子態依舊滿足歸一化約束，所以量子門相應矩陣U須為酉性［19］，即U*U=I，U*為U的共軛轉置。因此，量子態的制備和任何對量子態的操作都是酉操作，量子門是對所選量子位進行酉操作的算子。

按照操作涉及的量子比特的個數，可以將量子門分為單量子比特門和多量子比特門。單量子比特操作中常用的有Hadamard 門、Pauli-X 門、Pauli-Y 門、相位門（S 門）等，多量子比特操作中常用的有CNOT門、受控Z 門（CZ 門）、Toffoli 門等。表1 列出了常用的量子門及其矩陣形式。

表1 常用量子門Table 1 Frequently-used quantum gates

以Hadamard 門為例，假設一個目標量子比特為k的Hadamard 門，其概率幅計算和操作更新規則為：

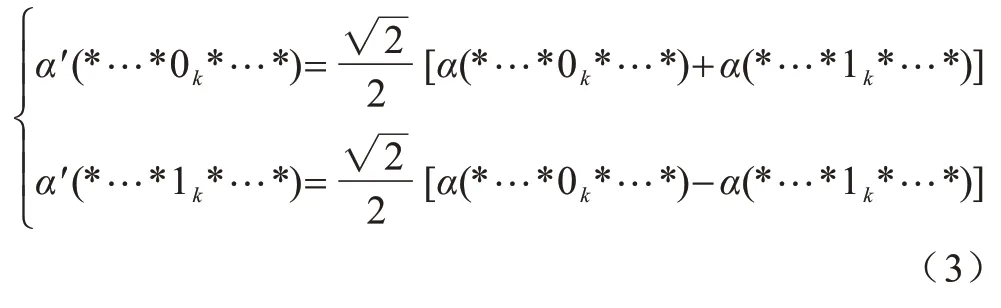
1.3 量子線路

量子算法由一系列基礎的量子門組合而成，實現的形式稱為量子線路。量子線路以量子比特為基本存儲單元，將量子邏輯門連接在一起來實現特定的計算功能，可以直觀地表示量子算法的結合和復雜度。本質上，量子計算可以描述為對包含量子比特的量子系統實施一系列酉變換，然后對變換之后的狀態進行測量，最后得到計算結果的過程。因此，量子計算的過程包括初態設置、狀態變換和測量3 個步驟。圖1 為2 個量子比特的Grover 搜索算法線路圖［1］，其中每一條線代表一個量子比特，量子門操作使用不同的方塊表示。

圖1 Grover 算法示意圖Fig.1 Schematic diagram of Grover algorithm

量子優越性是量子計算研究過程中的一個重要里程碑，指現階段實現針對特定問題的計算能力超越經典超級計算機。為研究量子優越性，研究人員提出了一些非常適合于展現量子設備計算能力的特定問題，包括隨機量子線路采樣（Random Circuit Sampling）［9，20］、IQP（Instantaneous Quantum Polynomial）線路［21］、高斯玻色采樣（Boson Sampling）［22-23］等。谷歌量子研究團隊所針對的問題是隨機量子線路采樣問題，中科大團隊則致力于高斯玻色采樣問題的研究。

如圖2（a）所示，谷歌的Sycamore 隨機量子線路是在特定圖結構上，周期地作用單量子比特門和兩量子比特門，且最終以單量子比特門結束［9，24-25］。單量子比特門均勻隨機取自于一個單量子門的集合，兩量子比特門表示為：

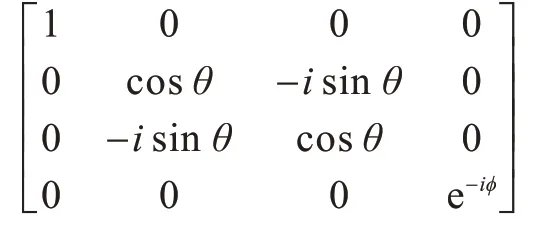
其中，θ=90°，φ=30°。隨機量子線路采樣問題是一個足夠復雜且又適合當前帶噪聲量子計算機求解的計算問題，能夠以較少的門操作數量來實現較大糾纏的量子態。隨機量子線路采樣成為最近展現量子優越性的主流候選問題，主要有3 個原因：1）隨機線路采樣問題非常適合于在二維結構的超導量子計算芯片上實驗實現；2）已有很多理論工作證明了隨機線路采樣問題的困難性；3）隨機量子線路采樣滿足反集中（anti-concentration）性質，表現為噪聲對輸出結果的概率造成的影響更小。

如圖2（b）所示，玻色采樣過程的模擬是計算給定輸入光子分布時得到某種輸出光子分布的概率，其最重要的部分在于求解矩陣積和式，而計算復矩陣的積和式對經典計算機來說是很困難的。

IQP 線路代表一類簡化的量子線路模型，如圖2（c）所示，線路的初始量子態都為零態，首先對每個量子比特作用一個Hadamard 門，然后在這些量子比特上作用對角的門，最后再次在每個量子比特上作用Hadamard 門。

圖2 研究量子計算優越性的3 種量子線路Fig.2 Three quantum circuits for studying quantum advantage

1.4 量子操作系統

量子操作系統是量子計算機資源的管理者，負責管理、監控、配置量子位硬件資源，調度量子程序運行的先后順序，控制量子程序單獨或并發映射，并提供具體的量子線路映射策略，保證量子程序的可靠度。為了充分利用量子計算機強大的計算能力，文獻［26］倡導建立量子操作系統來管理量子計算機的硬件資源。文獻［5-6］在國內率先開展了量子操作系統的原型研制，提出QuOS 原型，用于并發多量子程序在量子芯片上的映射、調度和優化。該系列工作設計了優化健壯量子位資源利用率的程序映射策略、跨程序量子位交換的映射方法和多量子程序調度機制，為量子操作系統軟硬件棧的設計和優化提供了原型系統和參考經驗。

1.5 量子模擬

目前，由于量子計算機的真機仍處于發展階段，通常單機可用的量子位數量較少（在100 以內）且量子位狀態保持不穩定，不能完成有實際意義的、較大規模的量子運算。在未確定量子硬件實現方案之前，很多量子算法所展現出的巨大計算潛力并未得到真機的實驗驗證，而主要是基于數學理論或者基于經典計算機的形式進行模擬驗證。

量子計算機除了和經典計算機有相似模型之外，還存在一些特有的計算模型。比較常用的量子模型包括量子線路模型、絕熱量子計算模型、One-way 量子計算模型、拓撲量子計算模型等。雖然這些模型設計的出發點不同，但計算結果的輸出是一致的，且相互之間可以進行轉化。在處理某類特定問題的計算中，采用不同的算法計算復雜度可能不同，而選擇一款好的計算模型能夠簡化算法的實現流程。

采用超級計算機模擬量子計算的過程，是目前研究量子計算、輔助量子計算機執行任務的一種方式。國內外科研機構、公司、高校積極開展了相關研究。量子模擬內涵豐富，本文將從量子計算模擬方法、國內外量子模擬器、超算集群模擬等方面進行深入介紹。

2 量子計算模擬方法

量子計算模擬主要是通過輸入不同的矩陣來改變要計算的量子態的狀態，從而引起量子線路狀態的變化。但在量子線路中，由多個量子邏輯門級聯而成對于邏輯門的操控精度提出極高的要求，若量子比特門的保真度不高，逐級增大，則會嚴重影響最終計算結果。受制于量子比特自身的物理特性，計算錯誤的發生常常無法避免，但可以避免錯誤對最終計算結果的影響。此外，評估量子計算中的錯誤嚴重性，對于改進器件的設計、優化控制參數以及使用緩解協議最小化錯誤至關重要。

2.1 量子計算概率幅模擬

量子計算概率幅模擬方法通過對概率幅的計算在經典計算機上實現對量子計算的模擬，在量子線路模擬過程中，通過計算一個量子線路后終態在各個基態上的概率幅獲取量子計算的模擬結果。該方法可分為全概率幅模擬和單概率幅模擬，其主要區別在于，全概率幅模擬一次模擬計算能夠計算出量子態所有概率幅，而單概率幅模擬只能計算出所有概率幅中的一個。除此之外，還有部分概率幅模擬的目的是在更低的硬件條件下實現更高的模擬效率。

全概率幅模擬方法直接計算并存儲全部量子態，計算的空間復雜度隨模擬的量子比特數指數增加。以n個量子比特為例，需要計算2n個復數形式的量子態來描述該量子系統，如果采用雙精度浮點數表達概率幅，則需要存儲空間的量子態為24+nByte。目前，即使在大型超級計算機上，也很難模擬一個超過50 個量子比特的量子線路。一方面，一個包含50 個量子比特的線路，完整的狀態有250個，即使采用單精度浮點來存儲，也需要約4 PB 的內存空間，這幾乎達到了當今超級計算機可使用內存的最大值；另一方面，即使超級計算機的內存夠用，處理這些海量數據也比較困難，原因在于數據在超算系統的網絡傳輸中將產生巨大的通信負荷［27］。

薛定諤方法和費曼方法是2 種經典的量子計算模擬方法。薛定諤方法存儲全部量子態，按順序計算作用不同量子門后的全部振幅，對于n個量子比特所需的24+nByte 的內存，每個量子門需要O（2n）的計算時間，對于深度為m的量子線路，所需模擬時間約O（mn2n）。費曼方法［28］對于終態的每個分量，枚舉通過量子線路中量子門能從初態到這一態的變化路徑，將所有這些路徑的值累加即可得到對應的概率幅，計算過程中存儲一條路徑最多需要O（n2m）的空間，對于深度為m的量子線路，計算一個狀態的振幅需要的時間為O（2mn）。文獻［8］將上述兩種方法相結合，提出薛定諤-費曼方法，以達到平衡算法時間和空間復雜度的目的。此外，研究人員還提出了數據壓縮［29］、輔助變量［30］、MPS［31］、PEPS［32］、部分振幅模擬［33］等方法，使得45 個量子位以上全概率幅的大規模量子計算模擬得以實現。

在量子計算模擬中，可將量子線路轉換為具有酉正性的特殊張量網絡表示，其單個概率幅的計算可以轉換成張量網絡縮并問題。張量網絡縮并算法不直接存儲實時的量子態，而是將初始量子態和測量基矢當作很多一維張量，這些張量和量子門操作組成一個時間和空間維度上的三維張量網絡。如何對一個包含數百節點的高維張量網絡選取一條接近最優的張量收縮路徑，是張量網絡收縮算法的關鍵問題。

文獻［18，34］采用張量網絡方法計算特定量子基態的概率幅，在模擬過程中利用對角矩陣縮減計算項數，并采用無向圖模型優化張量網絡縮并順序，從而減小張量網絡縮并開銷。文獻［35］改進張量網絡縮并順序優化算法，使其適用于分布式集群，并利用分布式計算的特性，將張量網絡計算任務拆分為多個子任務，使每個子任務的執行時間盡可能短，最終在阿里云集群上用1 PB 內存實現了81 量子位、40 深度的量子線路模擬。

谷歌提出的隨機量子線路結構是一個高度正則的張量網絡。當張量網絡縮并時，正則性將會表現為占用大多數計算時間的節點，構成一條“主干”，幾乎所有的運算時間都花在節點個數相較“分支”節點較少的“主干”上。文獻［8］提出一種基于張量網絡收縮的模擬方法，該方法主要分為圖劃分、局部優化和動態切片3 個步驟。首先，將張量網絡的節點劃分為若干塊，包含“主干”和“分支”部分，持續重復對“主干”部分劃分直到縮并成點后，對剩下的點再進行計算縮并。通過識別和優化這樣的“主干”，該方法計算速度可以比谷歌的模擬算法快200 000 倍。

文獻［32］基于張量網絡態來求解隨機量子線路采樣問題。張量網絡態算法可以認為是對張量網絡收縮算法選取了一條特定的收縮路徑，即先收縮時間維度，再收縮剩下的空間方向的二維張量網絡，通過對節點上的張量利用奇異值分解或QR 分解進行自動壓縮，以降低節點張量的維度。

文獻［36］提出Big-Head方法，并使用60個英偉達GPU 組成的小型計算集群，在5 天時間內完成了谷歌量子隨機線路的模擬。Big-Head 方法將終態的n個量子比特分為兩組，數量分別為n1和n2。任意位串s 可視作兩條位串s1和s2的拼接，其概率可計作PU（s）=PU（s1；s2）。當n2=0 時，該方法和張量網絡的單概率幅估算一樣。Big-Head 中最重要的環節就是找到一個滿足上述條件，時間與空間復雜度都比較合適的縮并階數，其使用分割算法將整個張量網絡切割成Ghead與Gtail兩份，切割邊nc條。分割算法會在對n1和n2數量限制的基礎上最小化。要找到分割點，需要保證同時縮并2 個部分的計算復雜度不會太大，為了達到這個目的，其使用一種聚類算法將每個子圖都分割成更小的子圖，直到每個子圖都足夠小。

常見量子計算模擬方法的特點及優缺點如表2所示。全概率幅模擬方法的計算復雜度隨模擬量子線路的深度線性增長，因此該類方法適合模擬具有較少量子比特數、任意深度的量子線路，適用于需要獲取全部模擬結果等場景。部分概率幅模擬方法的效率高，相比于全概率幅模擬方法能夠模擬具有更多量子位的淺深度的量子線路。張量網絡態算法可以用幾乎相同的模型來研究不同硬件架構下不同深度的隨機量子線路，原因在于其通常存在一個簡單的路徑搜索算法，僅需尋找一個數十個節點的平面圖上的最佳收縮路徑，因而實現起來只需要很少或者完全不需要經驗性參數。張量網絡收縮算法則往往需要考慮具體線路來確定其經驗參數，相比而言，其在更大空間搜索最優路徑，具有更大的優化空間。

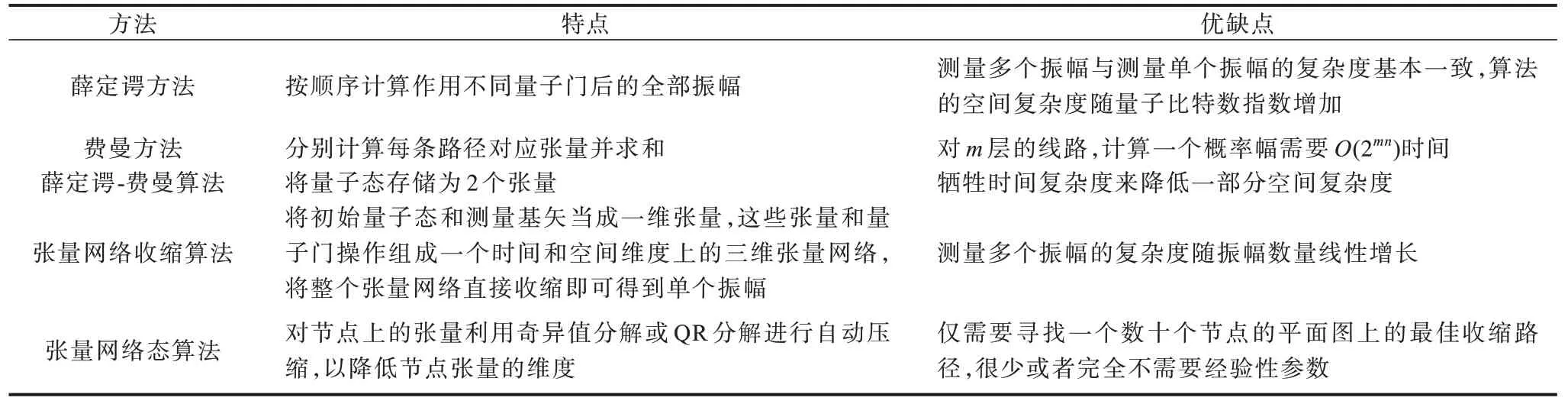
表2 常見量子計算模擬方法特點及優缺點Table 2 Features，advantages and disadvantages of common quantum computing simulation methods

2.2 針對Clifford 線路的量子計算模擬

量子比特通常是不穩定的，為了維持邏輯量子比特的準確性，需要進行量子糾錯。與傳統的糾錯方法不同，由于量子不可克隆定理、量子疊加態塌縮（或稱波函數塌縮）的限制，對量子比特進行糾錯必須加入輔助量子比特。相對于經典比特，量子比特還存在相位上的錯誤，這也為量子糾錯帶來了更大的復雜性，通常需要上千個物理量子比特來實現一個高保真的邏輯量子比特，而這也會為系統帶來大量的噪聲。針對容錯、抗退相干、保護目標數據的準確存儲，以及正確編碼、運行等問題，目前研究者提出了一些解決方案，包括無消相干子空間（Decoherence Free Subspace，DFS）、拓撲量子計算、基于量子糾錯碼的容錯量子計算等［37］。

針對因噪聲而導致的計算錯誤問題，可以使用量子糾錯碼來解決。在計算錯誤的分布滿足某些條件的情況下，可以把最終計算結果出錯的概率降到任意低，這被稱作容錯量子計算。與經典糾錯相比，量子糾錯不僅需要處理比特錯誤，而且還需要處理相位錯誤。容錯量子計算在量子計算碼的基礎上，通過級聯的方式實現量子邏輯門，以至于當物理操作的出錯率低于容錯閾值時，量子邏輯門的錯誤率急劇降低，從而實現可靠的量子計算。

量子糾錯碼與級聯結合，滿足容錯量子計算要求，橫向實現量子邏輯門，使得錯誤的位數和傳播控制在量子糾錯碼的糾錯范圍內。在量子糾錯碼上，可以橫向實現的量子邏輯門基本來自于Clifford 群。Clifford 群是指把Pauli 群共軛映射到Pauli 群的操作形成的群，包括Hadamard 門、相位門S 和受控非門CNOT 等。

Stabilizer codes 是一種基于穩定子的定義通用量子糾錯碼的框架，用以表述和操作需要的量子態，其使用Clifford group 中的量子門對穩定子態進行編碼和解碼。拓撲碼是一種比較容易實現的編碼方式，其可構造局域的穩定子測量來避免遠程的量子比特的交互，從而降低對設備的要求。拓撲碼的一個顯著的優點在于，人們可以通過增加單位晶胞的大小來提升檢錯和糾錯的容量。然而，隨著編碼容量的增大，解碼的任務必然會對量子態造成干擾，因而設計有效的解碼算法成為拓撲碼最重要的任務。表面碼的關鍵問題在于，要使用它來實現通用量子門集合是比較困難的，因為其缺少Toffoli 門以及π/8 門。在容錯量子計算的標準模型中，通常使用魔法態注入過程來構造一個完整的量子門集合。

隨機基準測試［38］和量子過程層析（Quantum Process Tomography，QPT）［39］可以分別測量噪聲量子信道的平均門保真度和完整信息，但這2 種方法只在幾個量子位系統中是有效的。交叉熵基準測試可以用于驗證多量子比特系統，但無法直接應用于經典計算機不可模擬的量子線路。量子計算機的并行計算能力隨量子比特數目增加而指數上升，同時，表征量子線路誤差的難度也指數上升［9］。文獻［40］提出一種基于Clifford 采樣的方法來描述量子線路的誤差，克服了現有誤差表征方法的不足，但只適用于少數幾個比特的量子線路，很難被用在未來成百上千個量子比特的量子線路表征中。Clifford 采樣將一個指數復雜度的問題轉換成多項式的問題，具有很好的可擴展性，適用于大規模量子線路參數的優化以及篩選等多個領域。

Gottesman-Knill 定理表明，一個僅由CNOT、Hadamard 門和相位門組成的量子線路可以在經典計算機上有效模擬。文獻［41］改進了定理中的算法，去除對高斯消元法的依賴，并給出2 種穩定態內積計算的有效算法。針對Clifford+T 門線路的模擬，研究者開展了一系列的工作，包括模擬包含少量T 門的量子線路和考慮nonstabilizer 的輸入態+Clifford 線路的模擬等［42-43］。為了解決量子線路的容錯和可靠性問題，研究者提出了量子線路的一系列結構等效規則和優化操作策略，以盡量減少T 門的數量，增加T 門的深度，最小化線路級，減少容錯實現代價并提高線路可靠性［44］。

2.3 針對含噪聲線路的量子計算模擬

NISQ 設備的計算能力對于量子信息科學具有基礎和實際重要性。如果沒有減少或繞過物理噪聲的策略，在苛刻的條件下任何量子程序的執行都可能會失敗。降噪技術的策略是設計更穩健的量子位來延長時間，以及執行更精確的門操作以提高可靠性等。隨機編譯是一種常用的策略，即在量子線路中插入隨機門。所有相干誤差和非馬爾科夫噪聲都可以轉換為隨機泡利誤差，在保留一個量子線路邏輯操作的同時誤差容易被檢測和糾正。雖然噪聲對單個隨機線路的影響可能有所不同，但在多個隨機線路上的預期噪聲被打亂，并調整成一種簡單的隨機形式。

文獻［45］考慮了在對稱或非對稱去極化噪聲下一大類隨機通用量子線路，并證明了如果每個量子門的噪聲是恒定的，那么這些量子線路的輸出可以用系統大小的時間代價多項式進行經典有效的模擬。文獻［46］結合了純態分解和低維基投影的思想來有效地模擬噪聲量子線路，提出將混合密度矩陣分解為一個類似于純態集合的低秩矩陣，將門和Kraus 運算子應用于該低秩矩陣，并計算了輸出密度矩陣和概率分布。該過程包括對密度矩陣的迭代壓縮，可保持一個具有最小誤差的數值緊湊形式。

3 量子計算模擬器

量子模擬器是在經典計算機上實現對量子計算機的模擬。近年來，基于量子計算原理，國內外許多公司機構設計并開發了大量的量子模擬器，如QisKit 量子模擬器（IBM）［47-48］、QDK 量子模擬器（Microsoft）［49］、太章量子模擬器（阿里巴巴）［10-11］等。現有的量子模擬器規模仍屬于NISQ 模擬器，模擬量子比特數在100 以內，主要受限于經典計算機的存儲技術和處理能力。本文系統梳理了國內外常見的量子計算模擬器，如表3 所示。

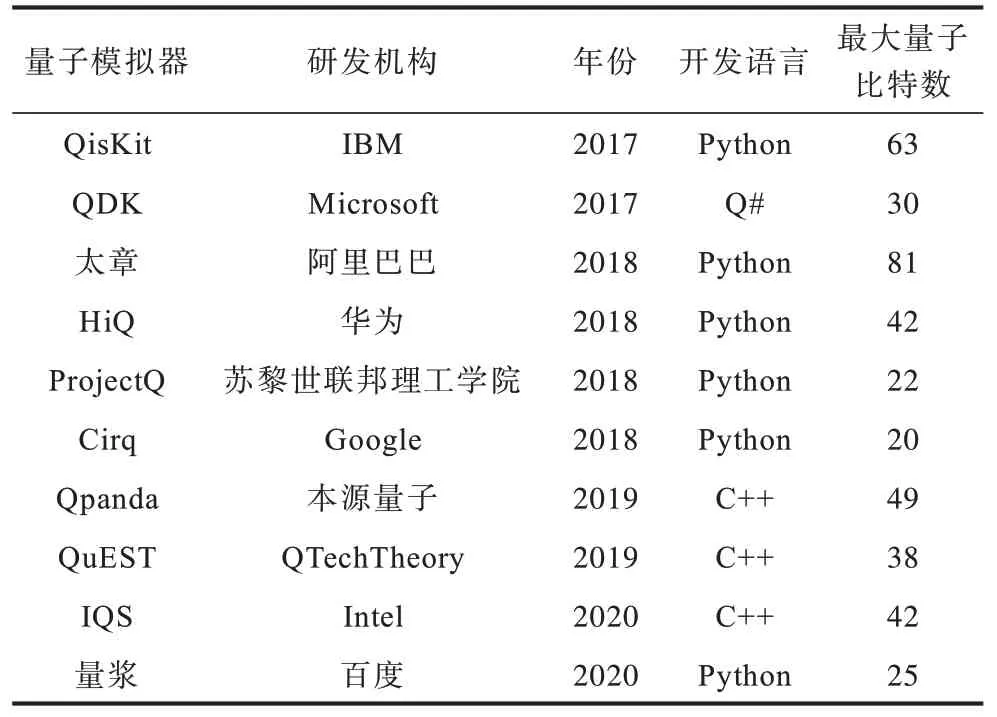
表3 常見量子計算模擬器Table 3 Common quantum computing simulators

QisKit［47］是由IBM推出的Python量子開發工具集，包含Terra（量子計算基礎庫）、Aer（帶有噪聲的模擬器）、Aqua（量子算法）、Ignis（檢測和去除實際量子計算機噪聲）四大組件，該量子模擬器可用于機器學習、自然科學、經濟金融領域以及解決最優化問題。

QDK［49］是Microsoft 推出的Q#量子開發工具集，Q#是一款面向量子計算機開發的程序語言，其結合了Python、C#等多種語言的設計元素，對量子計算機的邏輯進行了高度的封裝。QDK 包括Q#編譯器、量子庫和量子模擬器，該量子模擬器可應用于量子機器學習、量子化學等領域。

太章［10-11］是阿里巴巴推出的Python 量子開發工具集，目前最高存儲不到60 量子比特的量子態，太章采用張量網絡收縮的動態拆分辦法，減少了量子線路模擬的資源占用，支持量子算法和糾錯。

HiQ［50］是華為推出的Python 量子開發工具集，包括華為HiQ 量子模擬器、HiQ Pulse、HiQ Fermion等功能模塊，目前主要應用于量子化學領域。

ProjectQ［16］是蘇黎世聯邦理工學院推出的Python 量子開發工具集，其提供了量子模擬器、編譯器框架、編譯器插件、資源估算等模塊，可實現量子和量子線路的模擬。

Cirq［51］是谷歌推出的Python 量子模擬器，用戶可通過Cirq 實現對量子線路的精確控制，同時開源的OpenFermion-Cirq 可應用于量子化學領域。在Cirq 的基礎上，谷歌應用量子機器學習原理設計開源TensorFlow-Quantum（TFQ），該框架可有效解決量子分類、量子線路優化等問題。

Qpanda［52］是本源量子推出的C++量子工具集，其在量子模擬器基礎上實現了大量量子算法，如量子近似優化算法（QAOA）、Deutsh-Jozsa算法、Grover算法等。

QuEST［18］是牛津大學QTechTheory 團隊推出的C++量子模擬器，其在模擬基本量子計算的基礎上，支持CPU、GPU 多平臺運行。

為了安全庫存模型求解的合理性，需要做出以下假設：（1）生產線不允許缺料停線，停線費用設為無窮大。（2）庫存的消耗是連續且均勻的，即假設生產線是以恒定生產節拍進行消耗的，速度V線性消耗的，V是常數。（3）庫存的補貨時間遠遠小于周期運行時間，在此忽略不計。（4）庫存的補充間隔時間大于等于Milk-run系統的周期時間，記為T。（5）為了應對生產波動需要設置安全風險系數γ，增加安全庫存量來應對可能的風險。Milk-run線邊庫存模型一次補充量P必須滿足T時間內生產線的消耗，其物料的安全庫存量設置為：

Intel Quantum Simulator（IQS）［53］是Intel 推出的C++量子模擬器，前身為qHiPSTER，其提供了高性能計算功能，可支持用戶通過超級計算機進行模擬。

量漿［54］是百度推出的量子模擬器，其支持量子神經網絡的搭建和訓練，提供了多個量子機器學習案例，如量子近似優化算法（QAOA）、變分量子特征求解器（VQE）、量子神經網絡的貧瘠高原效應（Barren Plateaus）、量子分類器（Quantum Classifier）等。

目前，量子模擬器屬于NISQ 模擬器，在未來幾年，提升量子比特數、優化量子模擬器、構建模擬器上層軟件將成為量子模擬器的研究熱點。

4 基于超算集群的量子計算模擬

超級計算機集群為量子計算的模擬提供了硬件平臺，基于超算集群的量子計算模擬主要涉及以下2 項影響性能的關鍵問題：

1）任務拆分。任務拆分即拆分量子線路為多個子線路，并將其分配至不同的節點進行計算。任務拆分的目的是利用超算集群的運算性能來應對量子計算模擬帶來的海量存儲和計算資源開銷問題。合適的任務拆分策略可協助提升模擬性能，縮減節點間通信開銷，允許更多任務被拆分為子任務并行計算，充分利用超算集群的并行處理能力。

2）通信優化。通信優化涉及2 項優化內容：節點間通信次數以及單次通信傳輸數據量（單次通信開銷），這2 項優化內容之間亦可進行權衡。不合理的通信策略可能造成節點間帶寬擁堵、通信延時增加、節點數據饑餓等問題，因此，進行通信優化是提升超算集群運算性能的關鍵。

下文分別闡述任務拆分和通信優化的代表性工作。

4.1 任務拆分

現有的量子線路拆分方法通常采用分割多線路量子門操作的方式來拆分。拆分一個多線路門操作可生成多個小規模的子線路。將子線路分別執行后的結果進行合并，可得到原線路的執行結果。文獻［33］為了能夠在經典計算機上模擬更多量子比特，提出了一種“slice”的方法，將原來可能存在糾纏的整個量子線路切割成2 個或多個互不糾纏的子線路，并按照這種方式在IBM Blue Gene/Q 超級計算機上完成了對49 個量子比特、線路深度為27 的量子線路以及56 個量子比特、線路深度為23 的量子線路的模擬，提升了經典計算機所能夠模擬的量子程序的規模。

如果在分割時把線路分割成不同的子部分而分割線遇到了CZ 門（見圖3（a）），那么必須考慮控制線路對目標線路所有可能的影響。當控制線路1 在當前狀態是|0〉時，CZ 門對目標線路2 不產生影響（見圖3（b））；當控制線路處于|1〉狀態時，目標線路則要經過一個Z 門操作（見圖3（c））。這樣，為了剝離一個CZ 門的糾纏，系統狀態在此處便產生了分支，而且使得子線路的個數翻倍。

圖3 糾纏量子線路分割示例Fig.3 Example of entangled quantum circuit segmentation

假如一個系統在分割前有N條線路，則全概率幅模擬需要的存儲空間為2N。應用分割法后產生了2 個各有N/2 條線路的系統，這個系統的存儲空間約等同于2×2N/2個量子比特。如果在分割時分割了n個CZ 門，則最終的空間需求為2×2N/2×2n=2（N/2+n+1）。對于有大量線路的系統，層數較少的模擬的確可以大幅減少內存的需求，但隨著層數的增加，所切割的CZ 門數量也會相應增加，降低了使用該方法的優勢。最終當n>N/2-1 時，該方法對內存的需求比不分割還要大，從而失去了應用價值。

基于上述方法，文獻［35］把6×7、7×8、8×8 的量子線路分割成尺寸大致相等的2、3 和4 個部分，并對這些線路進行了多達36 層的模擬。為了衡量線路模擬的困難程度，其定義了一個稱為Complexity in qubit的物理量。該物理量實際上等同于需要同樣內存大小的未拆分線路的量子比特數，如圖4 所示。可以看出，每分割一個CZ 門，系統的子線路個數便翻倍。

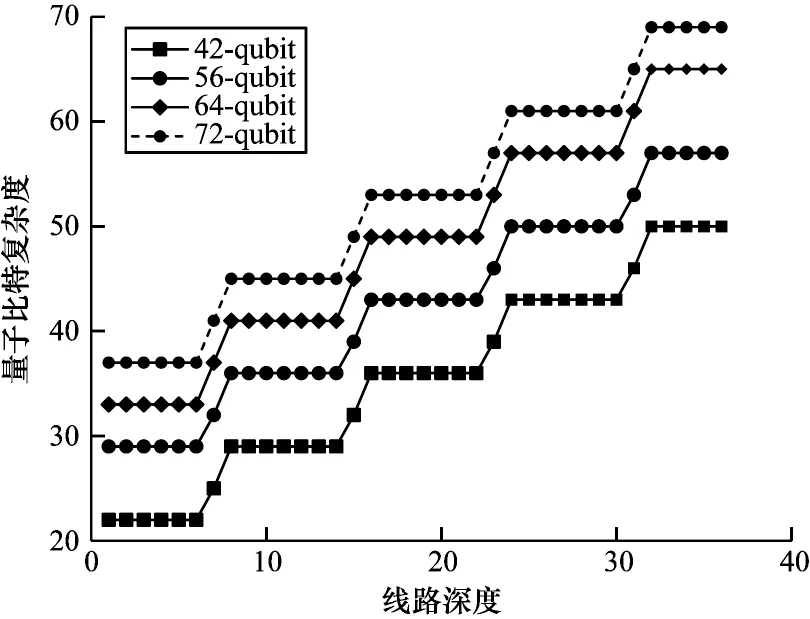
圖4 線路復雜度隨線路深度的變化Fig.4 Variation of circuit complexity with circuit depth

通過理論分析可發現，隨著深度的增加，線路復雜度呈單調增長，因為線路會遇到越來越多的CZ門。當所有深度的CZ 門總量接近線路大小的一半時（見上段），該方法就達到了一個臨界深度。使用該方法進行超過臨界深度的模擬會比不使用更加困難。當線路大小增加時，臨界深度也相應增加，因此，該方法適合用于大尺寸少深度的線路。

文獻［57］對分割法進行改進，提出了implicit decomposition 分割算法。該算法把線路分成不固定但有類似大小的三部分，分割線會隨著線路深度逐漸變化。implicit decomposition 算法對有4 個量子比特的線路的分割情況如圖5 所示。其中：A 部分有兩條線路，同時也分割了兩個CZ 門（門的狀態由線路2 上的b1 和b2 決定），因此，A 部分完整的狀態需要22×22=16 個概率幅來表示；B 部分本來也同樣需要16 個概率幅來表示，但由于線路2 在經過位置b2 后結束，因此該文作者認為b2 的狀態必須和線路2 的最終狀態一致，所以，B 部分的狀態向量可以減少一半的概率幅數。利用以上算法在“太湖之光”上能夠模擬7×7 個量子比特的39 層隨機線路，此規模已超過了在Blue Gene/Q 機器上同等量子比特數下的27 層模擬，達到了國際領先水平。

圖5 implicit decomposition 分割算法示意圖Fig.5 Schematic diagram of implicit decomposition segmentation algorithm

線路拆分方式側重點在于模擬更大的、擁有更多相互糾纏量子比特的線路，其可以達到的深度受多量子門總數的影響。如果一個線路含有較低密度的多量子門，那么該系統中各線路的糾纏程度就會較低，因此，也可以模擬更大深度的量子線路。

4.2 通信優化

在超算集群上進行量子計算模擬時，節點間和存儲間存在數據依賴，跨節點和設備的通信無法避免，因此，需要研究計算過程中的數據分布和數據傳輸方法以降低模擬過程的通信開銷。文獻［30］研究了量子算法中節點間的數據關聯性，針對量子計算每個量子門仿真過程中訪問的概率幅數據進行分析，提出一種MPI 進程間每個量子執行前進行的數據交互策略，從而降低節點間數據的關聯性，實現數據本地化，使通信頻率降低到多項式級。文獻［46］研究了異構眾核集群環境下的大規模量子計算模擬，提出通過最大化本地執行的量子門數量來降低通信頻率的方法，在異構眾核架構超級計算機Cori II 上實現了45 量子比特的量子計算機模擬實驗。文獻［59］為了解決不同GPU 之間的高數據依賴性，利用GPU Direct 技術設計并實現了使用GPU直接P2P 傳輸的方案，其使用4 塊GPU 進行多GPU的量子計算模擬，相較于libquantum 獲得了358 倍的加速比，并行效率達到0.92。

量子比特可以分為本地量子比特、節點內非本地量子比特和節點外非本地量子比特3 類。當量子門作用在非本地量子比特上時，會產生指數級的通信頻率問題。假設每個節點的內存空間可容納L位量子比特的所有概率幅，則模擬N位的量子比特需要2N-L個節點。如果對這些節點進行二進制編碼，那么量子態(aN-1…a2a1a0) 的概率幅將存儲在(aN-1aN-2…aL+1aL)號節點上的第(aL-1…a2a1a0)號位置，其中，ai∈{0，1}為第i位的量子態。例如，當N=5，L=2 時，系統使用了8 個節點來存儲所有概率幅，節點編號為（000）～（111），每個節點存儲4 個概率幅，編號為（00）～（11），則量子態（11010）的概率幅就存儲在第（110）號節點中的第3 個地址上。

由于所有概率幅分布儲存在各個節點上，因此一些門操作可能需要進行節點間通信。以單門H 為例，對第i條線路的單門操作需要更改量子態概率幅(…ai…)，此操作需要讀取和更新量子態系數(…0i…)和(…1i…)。當iL時，第(aN-1…0j…aL)和(aN-1…1j…aL)號節點上的概率幅需要互相交換信息，此時系統需要2N-1次MPI通信。第L至N-L位量子比特稱為全局（或“非本地”）量子比特。跨節點通信的延時要比節點內通信大很多，而且當通信過多時容易產生網絡阻塞，因此，本地量子位上的門操作相對全局量子位操作時間開銷更小。

假如要對第0 和1 位量子做一個CZ 門操作CZ0，1，即把所有A=(***01)的量子態與B=(***11)的量子態相交換（其中，一個*號代表一位量子態，為表達簡潔，把a4a3a2化簡為***）。由于第0 和1 位是本地量子比特，因此這個CZ0，1操作可以在各節點內快速交換(***01)和(***11)的數據來完成，如圖6 所示。另一方面，假如要對第3 和4 位的全局量子比特進行CZ3，4操作，那么概率幅C=(01***)和D=(11***)互換的操作就需要跨節點進行（此處***為a2a1a0），并要利用MPI 實行8次數據交換，運算時間要比CZ0，1長得多。如圖7所示：當進行CZ0，1操作時，節點內進行1 次信息交換，交換位置由曲線標出；當進行CZ3，4操作時，節點間進行8 次信息交換，交換位置由直線標出。

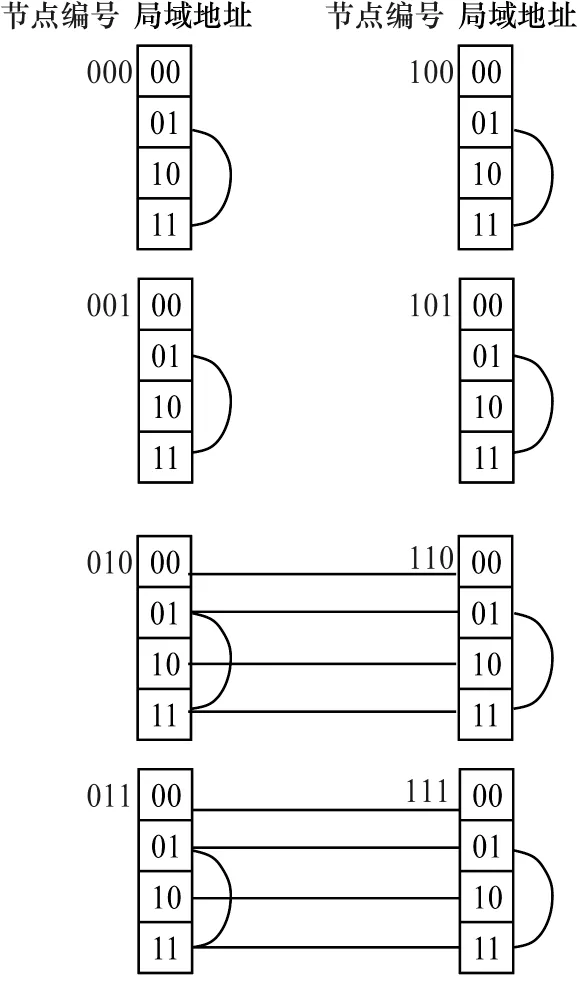
圖6 一個使用8 個節點儲存5 個量子比特的系統示意圖Fig.6 Schematic diagram of a system using eight nodes storing five qubits

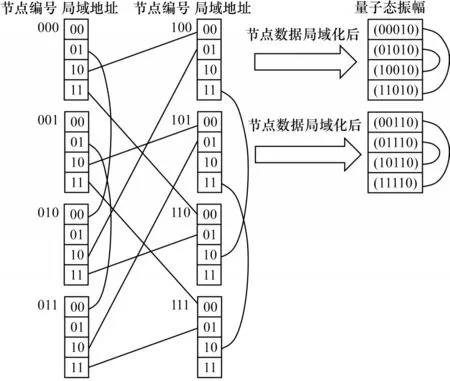
圖7 數據本地化示意圖Fig.7 Schematic diagram of data localization

CZi，j是一種比較簡單的操作，因為其數學表達矩陣只有4 個非零系數。對于一些比較復雜的門操作，例如XX Ising 門，所有存儲(00***)量子態概率幅的節點需要和存儲(11***)的節點通信，存儲(01***)和(10***)的節點也互相通信，共16 次。如果不對算法進行優化，全局量子位的計算將會變得很緩慢。

利用數據本地化的原理，可以把需要模擬的量子位從全局位置移至本地位置，移動后在節點內的內存中進行運算，從而大幅節省時間開銷［59］。

假設節點內存可容納的量子位數L不小于需要模擬的位數，以3、4 位的XX Ising 門為例，把第3、4 位量子比特的數據與第0、1 位互換，即：（00*01）與（01*00）互換；（00*10）與（10*00）互換；（00*11）與（11*00）互換；（01*10）與（10*01）互換；（01*11）與（11*01）互換；（10*11）與（11*10）互換。這6 組互換中的每一組實際包含了2 次互換，共12 次，少于優化前所需的16 次數據通信量。交換后，所有(**a2a1a0)數據都存儲在編號為(**a1a0a2)的節點內，各節點可以同時并行地執行門操作。

由圖7可以看出，經過12次數據交換后，第3、4位量子比特的概率幅(**a2a1a0)將會存儲在同一節點(a1a0a2)內，圖中右邊部分給出了經交換后節點（100）和（101）所存數據對應的量子態概率幅。操作完畢后，再根據下一個門所模擬的線路編號進行下一次的數據本地化，以此類推。

以此系統（N=5，L=2）為例，數據本地化方法能夠把任意復雜的雙量子門操作降低至12 次數據互換，而對于一些非常簡單的門操作，直接操作可能不需要12 次數據互換，這需要算法在模擬中作具體判斷。數據本地化還可類推用來優化多量子門操作，詳情不在此文展開。

5 結束語

量子計算模擬為量子計算機及量子算法的研究和驗證提供了有效的途徑。本文介紹量子計算模擬方法的研究進展，對不同方法的設計思路和優缺點進行對比分析，列舉目前常見的量子計算模擬器，并對利用超級計算機實現量子計算模擬的優化方法進行討論。大規模量子計算模擬全部量子態概率幅的方式所需內存資源隨被模擬的量子位數指數增加，可模擬的量子位數受到物理內存容量的制約，而部分概率幅模擬方法通過有效降低時間復雜度和空間復雜度，計算效率比全概率幅模擬方法更高，且在模擬過程中考慮線路的分割和數據的本地化，能夠在節點內用更少的時間并行完成門操作計算。此外，為實現量子計算的大規模實用化，糾錯、容錯技術也同樣需要發展。

目前，量子計算模擬在算法和工程上仍有很大的優化空間。在算法方面，張量網絡縮并的順序極大地影響計算效率，未來可探索更優縮并順序算法；在工程方面，需要應用張量運算來充分發揮硬件性能，進一步減少線路模擬所需的時間。同時，可擴展性和容錯也將是未來量子計算研究中的關鍵問題。