基于特征增強聚合的融合廣告點擊率預測模型

蔣興渝，黃賢英，陳雨晶，徐 福

（重慶理工大學計算機科學與工程學院，重慶 400054）

0 概述

廣告點擊率（Click-Through Rate，CTR）預測的目標是根據廣告信息和用戶信息預測廣告是否被點擊。在線廣告公司利用準確的廣告CTR 預測最大限度地吸引用戶并提高用戶粘性。廣告CTR 預測在推薦系統、智能信息檢索和金融領域被廣泛的研究與應用［1］，如何準確、有效地預測點擊率成為研究熱點。

CTR 預測的研究主要分為基于傳統機器學習的淺層模型和基于深度神經網絡（Deep Neural Network，DNN）的模型。基于傳統機器學習的淺層模型主要是邏輯回歸（Logistic Regression，LR）模型［2］。LR 模型具有易于實現可解釋性強的優點，但無法通過特征交互提取組合信息。文獻［3］提出Poly2 模型對所有特征進行兩兩交互，并對所有特征組合賦予權重，由于CTR 模型的輸入特征通常是由獨熱編碼［4］得到高維稀疏化二維向量，因此Poly2 模型具有大部分特征交互權重、缺乏有效數據訓練、訓練復雜度高的缺點。文獻［5］提出因子分解機（Factorization Machine，FM）模型，通過隱向量獲得元素級特征交互以減少計算開銷，FM 模型并未考慮不同特征組合攜帶不同的信息量，在實際情況中不同特征組合攜帶隱向量的信息也有所不同。文獻［6］提出特征域概念，在特征域感知因子分解機（Field-aware Factorization Machine，FFM）模型中每一維特征都歸屬一個特定域，而特定域和特征是一對多的關系。該模型進一步加強了特征交互能力，其計算時間開銷遠大于FM 模型，在實際使用中較難應用于純數值類型的數據集。文獻［7］提出基于FM 模型的注意力因子分解機（Attention Factorization Machine，AFM），在FM 模型的基礎上增加注意力機制，這個機制對元素級交互特征進行注意力加權，用于判斷不同特征之間交互的重要性，有利于模型發現并重視對預測結果有幫助的直接關聯特征交互，使模型具有記憶能力。由于最后直接加權累加，高階特征并沒有輸入更深的網絡模型以學習非線性交互特征，因此AFM 模型未利用DNN 的優勢。Poly2、FM、FFM、AFM 模型都是基于傳統LR 模型增加了對特征進行全交叉的自動學習權重部分，此外，利用GBDT 產生高維非線性特征的GBDT+LR［8］組合模型進行特征變換。

近年來，GPU 矩陣運算性能得到逐步提升，深度學習被廣泛應用在圖像分類［9］、機器翻譯［10］、對抗攻擊［11］等領域。基于DNN 的模型將深度學習運用于CTR 預測任務，通過DNN 學習復雜的高階特征交互模式。隨之出現基于因子分解機支持的神經網絡（FNN）［12］、基于乘積產生層的神經網絡PNN［13］等，FNN 和PNN 模型都充分考慮高階向量級特征的交互，卻忽略低階特征的重要性導致模型泛化能力不足。因此，文獻［14-15］提出Wide&Deep 和深度因子分解機DeepFM 模型，不僅考慮高階特征交互所攜帶的信息，同時也兼顧低階特征攜帶的信息。因此，Wide&Deep 和DeepFM 模型同時具有記憶和泛化能力，預測準確度優于之前的模型，但其記憶和泛化能力仍有提升的潛力。基于深度學習模型的共同點是利用嵌入層得到嵌入向量，并通過DNN 學習高階交互特征從而完成CTR 預測。

文獻［16］指出，由于不同特征級上的特征交互所含特征信息表達不同，因此最終模型的預測泛化能力也有所不同。在CTR 預測任務中，傳統模型都屬于單一特征級交互模型，在記憶和泛化能力方面有一定局限性。本文以并行結構結合AFM 和PNN模型，構建一種基于特征增強聚合的融合深度神經網絡（APNN）點擊率預測模型。將一階信息重要性嵌入原始數據的特征向量進行特征增強，利用注意力交互的元素級交互特征與外積操作得到向量級交互特征，并與增強一階特征進行融合，增強模型的記憶和泛化能力。在此基礎上，采用多個全連接層從融合特征中獲得高階特征之間的交互關系，從而計算得到CTR 預測值。

1 相關工作

1.1 特征編碼與嵌入

在CTR 預測任務中，數據集特征分為類別特征和數值特征，由于類別特征不能直接用于數值計算，因此通常會對類別特征進行One-Hot 操作，例如某種寵物食品廣告里，狗的性別特征可以用編碼表示為：雌性［1，0］、雄性［0，1］，共占2 bit；年齡特征按照幼年、成年和老年劃分，表示為［0，0，1］、［0，1，0］、［1，0，0］，共占3 bit。

獨熱編碼雖然解決了用于數值計算的特征表示問題，但每個特征的多個bit 僅有1 位表示某個特征，編碼后用于計算的特征向量呈現高維稀疏的形態，若直接將這樣的特征向量輸入神經網絡進行訓練，導致計算開銷大。因此，在輸入深度網絡訓練前，特征編碼需要增加1 個嵌入層來降低神經網絡訓練時的權重單元開銷。嵌入層可以將原來高維且稀疏的獨熱編碼映射為1 個低維且稠密的嵌入向量用于計算，例如性別域為雌性，年齡為16 歲的狗的獨熱編碼為［1，0，1，0，0］，其中前bit 表示性別特征，后3 bit表示年齡特征，假設將5 bit 的獨熱編碼映射為4 維的嵌入向量［0.8，0.2，0.9，0.1］，其中前2 維［0.8，0.2］表示性別特征，后2 維［0.9，0.1］表示年齡特征，能夠減少網絡中神經元數量和計算開銷。不同特征所對應的映射嵌入向量也是不同的。

1.2 注意力因子分解機模型

AFM［7］模型由基礎的FM 模型引入注意力機制演變而來。雖然FM 模型能夠發現二階組合特征，但是將所有交互特征的權重都視為相同，則降低FM 模型的效果，因為不是所有的特征組合貢獻度都是一樣的，某些無用的特征進行組合可能引入噪聲，降低模型預測性能。因此，AFM 模型引入注意力機制用于判斷不同特征級交互的重要性，使模型具有記憶能力。AFM 模型前3 個部分（Sparse Input、嵌入層、雙向交互層）與FM 模型是一致的。假設有N個嵌入向量，通過雙向交互層得到N(N-1)/2 個特征向量組合，每個組合向量都是由2 個不同的嵌入向量的元素級交互產生。AFM 模型的核心是注意力池化層，由上一層雙向交互層得到的特征組合被多層感知機（Multi-Layer Perceptron，MLP）經Softmax 歸一化得到重要性分數。

1.3 產生層的神經網絡模型

PNN［13］模型由嵌入層、產生層和MLP 組成，傳統方式是直接將MLP 與嵌入向量相連進行特征交互組合。該方式首先忽略了不同特征組合的特異性；其次MLP 并不是專門設計用于特征之間的交互計算。但在實際應用中，PNN 模型需要考慮不同特征之間的交互信息，例如1.1 節中性別和年齡在預測任務中是重要的分類特征，而兩者的組合特征同樣包含大量的高價值信息。因此，PNN 模型在嵌入層和MLP 之間設計的產生層不僅包含一階信息而且針對性地完成了向量級特征交互工作，同時由于產生層中不同求積方式，PNN 模型分為內積PNN（Inner PNN，IPNN）、外積PNN（Outer PNN，OPNN），其中OPNN 計算方式隨著網絡層數的增加效果優于IPNN，更適合深度神經網絡模型。通過這兩種內積方式捕獲不同特征交互信息，增強模型表征不同數據模式的記憶能力。

基于AFM 和PNN 在模型記憶能力上的研究，以及兩者對模型泛化能力忽略的部分，本文設計一種新的點擊率預測模型，在保持模型記憶能力的基礎上，同時提升模型記憶和泛化能力，使其能夠敏感地捕捉到對預測結果有幫助的特征和交互信息，并對稀疏甚至未曾出現的特征具有一定的預測能力。

2 APNN 模型

APNN 模型結構如圖1 所示，主要由6 個部分構成，原始數據經過嵌入門機制層獲得嵌入向量和一階信息重要性后，分別輸入注意力交互層、一階信息增強層和外積層，然后利用聚合層把它們輸出的特征拼接融合，最后將融合特征輸入深度網絡部分擬合出不同高階特征之間的交互關系，并通過sigmoid［17］激活函數計算得到CTR 預測值。

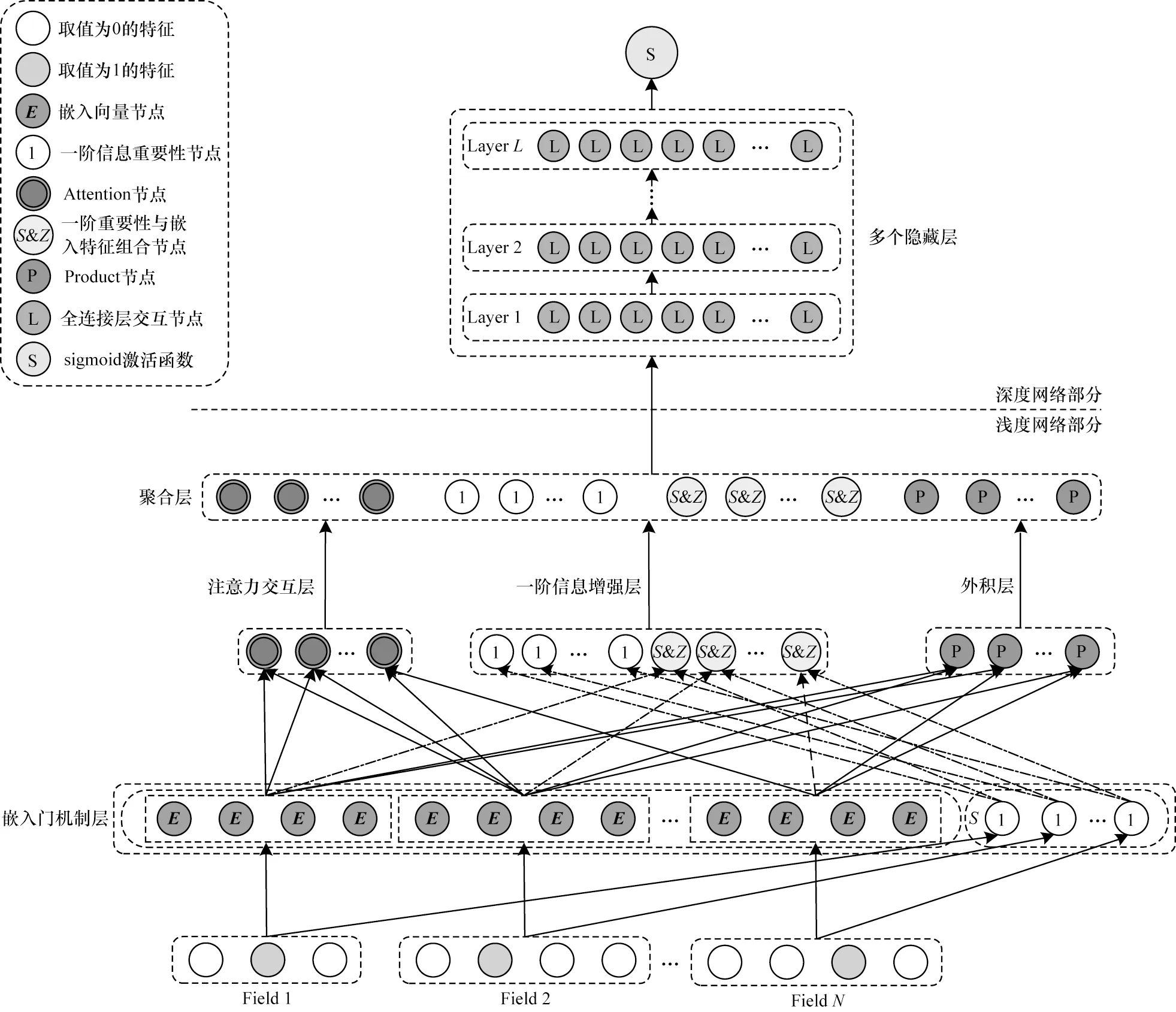
圖1 APNN 模型結構Fig.1 Structure of APNN model

2.1 嵌入門機制層

嵌入門機制層根據原始域特征得到嵌入向量E和一階信息重要性表示S。單獨表示的一階信息重要性使特征中的有效信息更加豐富，在預測時能夠作為新特征進行計算，加強模型記憶能力。以1.1 節提到的狗的特征信息為例，嵌入門機制層示意圖如圖2 所示。

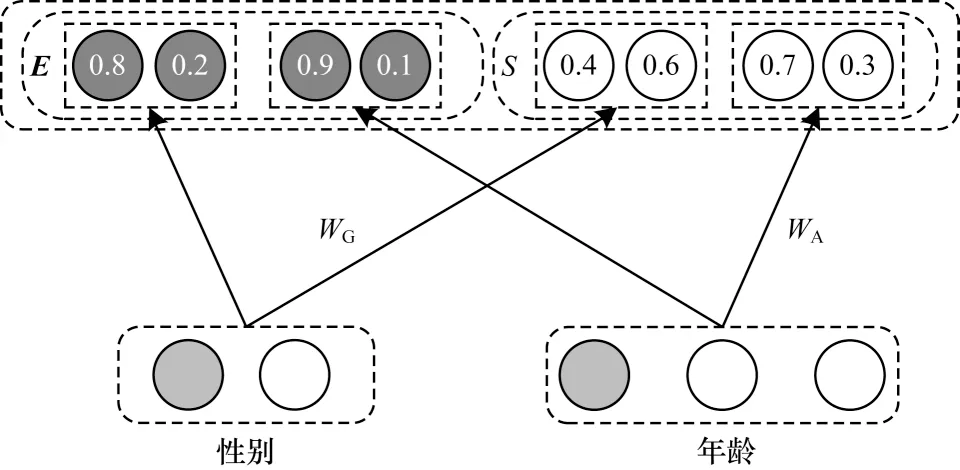
圖2 嵌入門機制層示意圖Fig.2 Schematic diagram of embedding and gate layer

嵌入門機制層表達如式（1）所示：

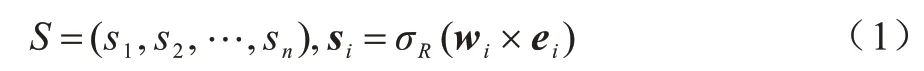
其中：si∈Rk為一階嵌入向量ei∈Rk的信息重要性；w∈Rk×k為k維嵌入向量ei的元素權重；σR為用于信息選擇的ReLU［18］激活函數。

嵌入門機制層經過參數WG、WA得出兩個可能對狗的健康產生影響的一階信息重要性向量，其中性別特征重要性向量為［0.4，0.6］，年齡特征重要性向量為［0.7，0.3］。嵌入向量和一階信息重要性通常有兩種訓練方式，一種是使用其他點擊預測模型，例如FM 模型進行預訓練得到，也可以參考DeepFM 模型的訓練方式。APNN 模型將嵌入向量與一階信息重要性向量代入模型進行統一訓練。通過嵌入門機制層計算各個特征域一階重要性表示和嵌入向量，并分別用于不同的特征交互層以挖掘特征交互組合中的深層信息。

2.2 注意力交互層

注意力交互層的輸入是嵌入向量，輸出是帶權的元素級交互特征A∈Rk，如式（2）～式（4）所示：

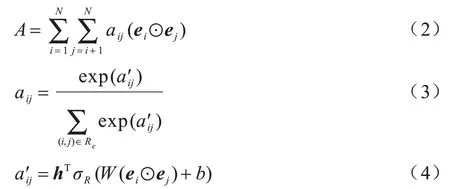
其中：aij為特征組合的重要性；ei為k維的嵌入向量；N為特征域的數量；Re為所有可能的特征交互組合；W∈Rt×k，b∈Rt，h∈Rt為模型參數；t為隱藏層節點數；σR為ReLU 激活函數；⊙為向量元素積。交互特征如式（5）所示：

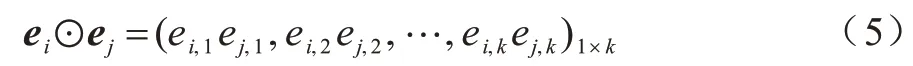
這種交互特征對分類貢獻程度較高的特征組合賦予較高的權值，采用的元素級特征交互能夠利用更多維度的向量元素，使融合后的交互特征所含有效信息更加豐富。

2.3 一階信息增強層

在一階信息增強層中加入特征重要性以增強一階信息，并利用元素積把一階信息重要性表示S嵌入向量E，如式（6）所示：

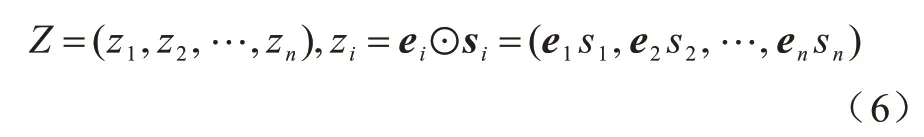
其中：ei∈Rk為第i個嵌入向量；si∈Rk為嵌入向量信息重要性；zi∈Rk為含有增強信息的一階信息節點，i=1，2，…，n；n為嵌入向量節點的個數；⊙為向量元素積。

在特征交互中，一階信息增強層引入嵌入向量元素的重要性，使得每個向量元素獲得獨立的重要性信息。在模型整體中，一階信息增強層引入一階信息節點的重要性以豐富模型提取的特征信息，從而獲得更準確的高階特征組合表示。

2.4 外積層

外積層在向量級上計算嵌入向量的外積矩陣g，然后通過權重矩陣W計算每個交互的貢獻度，如式（7）所示：

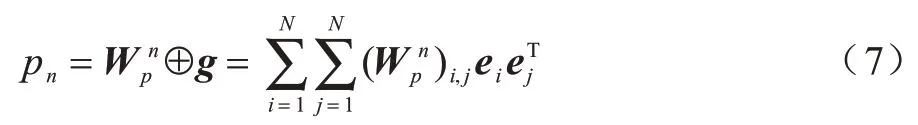
其中：ei∈Rk是經過嵌入層后的k維嵌入特征向量；為第n個節點的嵌入向量外積權重矩陣；N為特征域的數量；⊕為矩陣逐項相乘后全部相加。

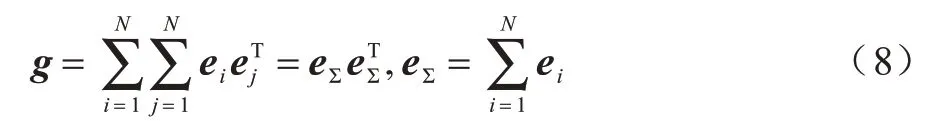
其中：eΣ∈Rk表示嵌入向量ei按域相加求和。聯合式（7）～式（8），得到：

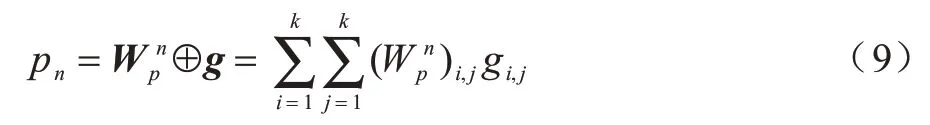
最后通過一個單隱藏層，把外積映射為D維的向量P=(p1，p2，…，pn，…，pD)，D是單隱藏層神經元數量，設置D=N(N-1)/2，N是特征域的數量。外積過程中由于求和池化損失的一部分信息，通過與注意力交互層的輸出融合彌補。

2.5 聚合層

聚合層是將注意力交互層、一階信息增強層和外積層輸出的對重要特征以及交互具有記憶能力的不同特征級信息進行拼接，得到同時具有記憶能力和泛化能力的融合特征數據c0∈Rk×(2N+1)+D=[A，S，Z，P]，其中A∈Rk是注意力交互層輸出，S∈RN×k是一階信息重要性表示，Z∈RN×k是增強后的一階信息節點，P∈RD×1是向量級特征交互。然后將拼接后的數據c0作為深度網絡部分的輸入，使拼接后的融合特征能夠進行高階交互。

2.6 深度網絡部分

深度網絡部分使用的DNN 由多個全連接層組成，其中DNN 的全連接層數量是可調的，當層數為0時，如果僅使用淺度網絡部分的輸出作為最終特征，通過sigmoid 函數激活后進行預測，則得到一個APNN-Shallow 模型，如式（10）所示：

其中：w0為輸出節點的偏置；wi∈Rk是第i個向量ei的權重；c(0)是聚合層輸出的融合特征；N為特征域的個數；σS為sigmoid 激活函數；∈(0，1)為CTR 任務所求的預測值。

為進一步使用DNN 捕獲高階特征交互信息，提升模型性能，本文將淺度網絡部分與DNN 串聯形成深度網絡結構。深度網絡部分的輸入是聚合層輸出的融合特征c0，如式（11）所示：

其 中：l為DNN 的層數；σR為ReLU 激活函數；W(l)、b(l)、c(l)分別為深度模型的權重、偏置以及第l層的輸出。深度網絡部分將生成的稠密實數特征向量c(l)送入sigmoid 函數中進行CTR 預測。本文在一定程度上增加少量全連接層以提升模型的精度。因此，APNN-Deep 模型的輸出如式（12）所示：

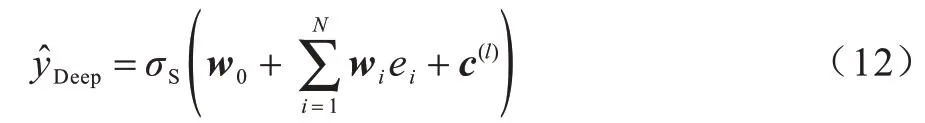
其中：w0為輸出節點的偏置；wi∈Rk是第i個向量ei的權重；N為特征域的個數；σS為sigmoid 激活函數；∈(0，1)為CTR 任務所求的預測值。APNN 模型旨在最小化式（13）中的交叉熵目標函數值：

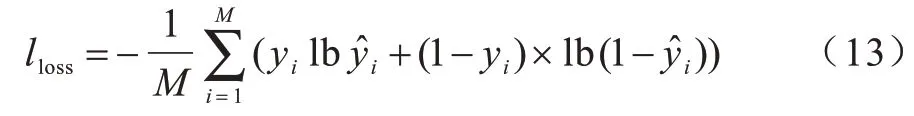
其中：yi和分別為第i個樣本的真實值和預測值；M為樣本的大小。APNN 整體算法流程如下：

算法1基于特征增強聚合的融合廣告點擊率預測算法

3 實驗及性能評價

本文通過Criteo 和Avazu 2 個公開數據集進行實驗，對APNN 模型的預測性能進行評價。首先對實驗使用的數據和評價指標進行介紹，然后對7 種作為對比CTR 預測模型進行描述，最后通過實驗數據展示APNN 模型的實驗效果，并對實驗結果進行討論。

3.1 實驗數據及評價指標

3.1.1 數據集

從2014 年起Criteo 和Avazu 數據集作為學術界衡量CTR 預測模型性能的基準數據集［14-16］，在各種研究中［19-20］被廣泛使用。Criteo 數據集是2014 年由Criteo公司在Kaggle 平臺上發起的展示廣告點擊率預測大賽的數據集，近年來被廣泛用于許多CTR 模型評估中。該數據集包含約4 500 萬條真實的用戶點擊反饋數據，其特征由26 個脫敏分類特征和13 個連續數值特征組成。本文實驗將數據集隨機分為兩部分：90%用于訓練，其余部分用于測試。Avazu 數據集是按照時間順序排列的不同日期廣告點擊數據組成。該數據集包含約4 000 萬個真實數據的用戶點擊反饋，每條廣告點擊數據有24 個特征。本文實驗將其隨機分為兩部分：80%用于訓練，其余部分用于測試。

3.1.2 評價指標

本文實驗采用AUC［21］和LogLoss［22］作為評價指標。AUC是評估分類問題中廣泛使用的指標。AUC是ROC曲線下的面積，其上限為1。此外，文獻［21］證明AUC在CTR 預測中是一種很好的評價標準。AUC 值越大表明模型預測性能越好。

LogLoss 是二分類問題中廣泛使用的評價標準，用于測量預測值與真實值之間的差距。LogLoss 下限為0 時表示預測值與真實值完全匹配。在實驗中，LogLoss 值較小表示預測模型的性能更優。

3.1.3 實驗超參數設置

本文在實驗中使用Tensorflow編碼構建所需模型。在使用Criteo 數據集時，實驗中的嵌入門機制層嵌入向量的維度設置為15；對于Avazu 數據集，嵌入向量的維度設置為50。本文使用Adam［23］作為實驗優化方法，對于Criteo數據集，最小Batch-Size為1 024；對于Avazu數據集，最小Batch-Size 為512。Criteo 數據集的每層神經元數為1 000，Avazu 數據集的每層神經元數為2 000。統一設置學習率為0.000 01，丟棄率為0.5，DNN的層數為3 層。

3.2 對比實驗模型設置

為驗證APNN 僅使用淺度網絡部分模型和深度網絡部分模型的性能，本文將實驗分為Shallow 組和Deep 組。實驗還將基線對比模型分為淺基線模型和深基線模型。淺基線模型包括LR［2］、FM［3］、AFM［7］，而深基線模型包括FNN［12］、PNN［13］、Wide&Deep［14］、DeepFM［15］。為了簡化對比實驗，深基線模型每個隱層節點的激活函數統一設置為ReLU，輸出節點的激活函數為sigmoid，最優參數求解都采用Adam。如果公司的用戶群數量非常大，則AUC 提高1 將為公司收入帶來大幅增長［14，24-27］。

3.3 性能評價及分析

本文通過6 組實驗對APNN 模型的性能進行評價。實驗1 是經典CTR 模型與APNN 模型的性能對比；實驗2 是增加DNN 對AFM 模型的性能影響；實驗3 是引入一階信息重要性對PNN 的性能影響；實驗4 是不同超參數對APNN 模型的影響；實驗5 是單一模型結構與融合模型結構的性能對比；實驗6 是不同改進對APNN 模型性能的影響。

3.3.1 APNN 模型與經典CTR 模型的性能對比

在Criteo 和Avazu 數據集上APNN-Shallow 與其他模型的性能對比如表1 所示。APNN-Shallow 表示淺層APNN 模型，與LR、FM、AFM 模型相比，APNN-Shallow模型性能最優。實驗結果表明，AFM、PNN 與增強一階信息融合后的APNN-Shallow 模型能夠有效提升實際任務的精準度。

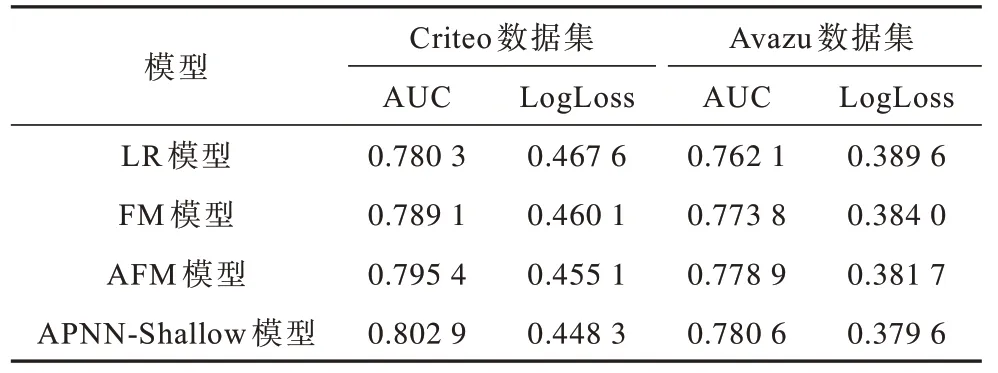
表1 在Criteo 和Avazu 數據集上APNN-Shallow 與其他模型的性能對比Table 1 Performance comparison of APNN-Shallow and the other models on Criteo and Avazu data sets

為進一步提升模型性能，在Criteo 和Avazu 數據集上APNN-Deep 與其他模型的性能對比如表2所示。APNN-Deep 模型由部分APNN-Shallow 和DNN 串聯組成。從表2 可以看出，APNN-Deep 模型提高了特征的高階交互學習能力：單一結構的深度學習模型FNN 與PNN 性能均優于Shallow 組模型的性能，其中在Criteo 數據集上基于FM 模型的FNN 模型的AUC 和LogLoss 性能指標上較FM 提高了1.63 和1.33 個百分點，PNN 模型的AUC 和LogLoss 性能指標較FM 模型提升了1.74 和1.42 個百分點。與其他Deep 組模型相比，APNN-Deep 模型具有更優的性能，說明融合后的模型結構可以挖掘更多對于CTR 預測有價值的信息，同時也表示隱含的高階特征相互作用有助于Shallow 部分獲得更多的表達能力。

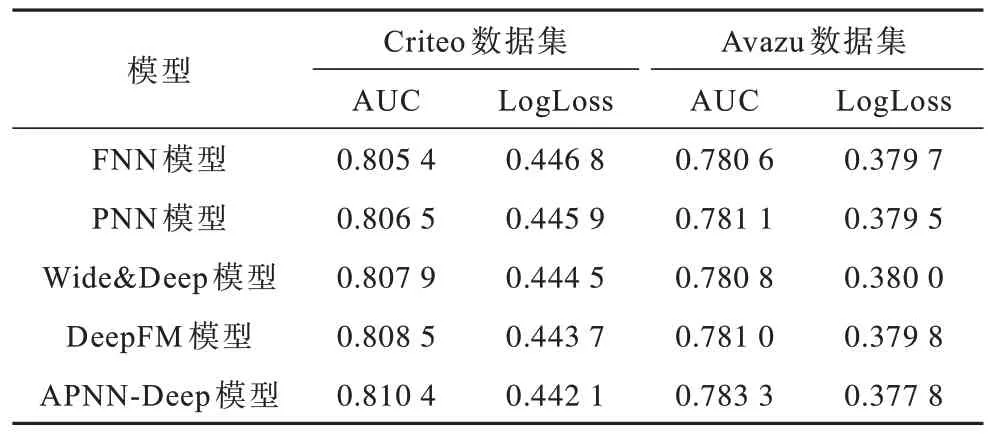
表2 在Criteo 和Avazu 數據集上APNN-Deep 與其他模型的性能對比Table 2 Performance comparison of APNN-Deep and the other models on Criteo and Avazu data sets

3.3.2 DNN 對AFM 模型的性能影響

APNN 模型的改進是將AFM 的帶權特征輸入到DNN 中，獲到注意力交互層后的高階特征交互信息。在Criteo 和Avazu 數據集上原始AFM 與增加DNN 的深度AFM（AFM-Deep）模型的性能對比如表3 所示。從表3 可以看出，本文增加DNN 后的AFM-Deep 模型具有較優的性能，在Criteo數據集上AFM-Deep的AUC指標較AFM 模型提高了0.11 個百分點，LogLoss 指標提高了0.12 個百分點。在Avazu 數據集上AFM-Deep的AUC 指標較原來的AFM 提高了0.37 個百分點，LogLoss 指標提升了0.34 個百分點。

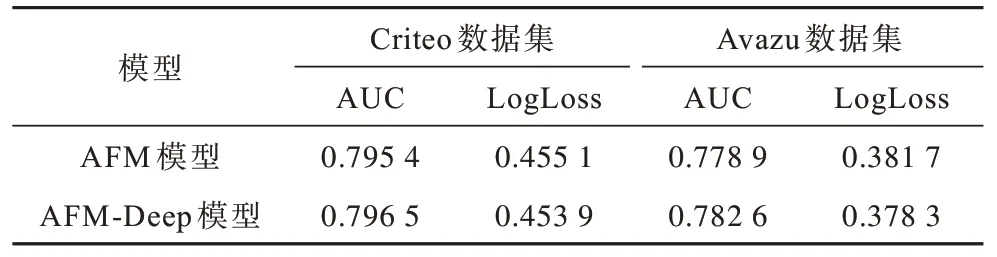
表3 在Criteo 和Avazu 數據集上AFM 與AFM-Deep模型性能對比Table 3 Performance comparison of AFM and AFM-Deep models on Criteo and Avazu data sets

AFM-Deep 模型性能提升的原因是通過將AFM訓練特征輸入DNN 并對特征進行更高階組合，一方面可以減少人工特征工程干預，另一方面通過DNN學習注意力特征交互后得到的特征，在一定程度上增強了模型挖掘高階特征交互信息的能力。

3.3.3 一階信息重要性的引入對PNN 性能影響

APNN 模型的另一個改進方法是引入一階信息的重要性，PNN 與引入一階信息增強層的增強PNN（Linear Feature Enhanced PNN，LFE-PNN）模型性能對比如表4 所示。從表4 可以看出，本文將一階特性重要信息引入PNN 模型能夠提升模型性能。

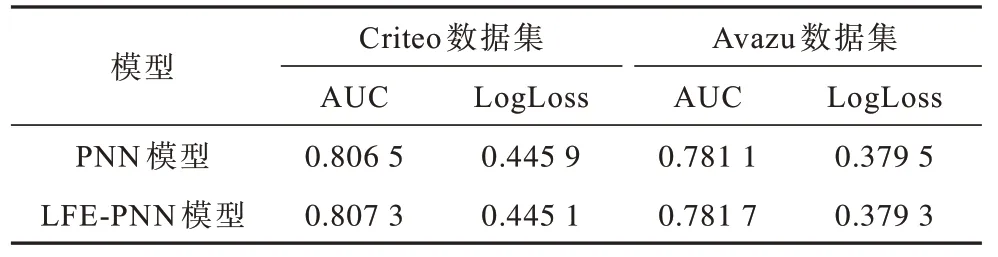
表4 在Criteo 和Avazu 數據集上PNN 與LFE-PNN模型性能對比Table 4 Performance comparison of PNN and LFE-PNN models on Criteo and Avazu data sets

相比PNN 模型，LFE-PNN 模型的AUC 指標分別在Criteo 和Avazu 數據集上提升了0.08 和0.06 個百分點，LogLoss 指標分別提升了0.08 和0.02 個百分點，其原因是LFE-PNN 模型在有效數據信息量上較PNN 模型有一定增加，通過DNN 挖掘高階信息后得到了更準確的特征表示。

3.3.4 不同模型超參數對APNN 模型的影響

本文對APNN 模型使用的超參數進行研究，并把研究重點放在嵌入層部分和DNN 部分，其中DNN 部分包含激活函數、丟棄率、DNN 深度以及DNN 中每層神經元的數量。為簡化實驗，本文僅研究DNN 的深度以及DNN 中每層神經元的數量，將更改以下超參數：嵌入層維度、DNN中每層神經元的數量、DNN的深度。本文使用的DNN 網絡超參數設置為3.1.3 節中的數據。

1）嵌入層維度對模型預測性能的影響

嵌入層維度的變化影響嵌入層和DNN 部分中參數的數量。本文將嵌入層維度按步長為5，逐步從5 更改為70。嵌入層維度對APNN 模型性能的影響如表5所示。從表5可以看出，隨著嵌入層維度從5增大到70，在Avazu 數據集上APNN 模型性能得到提升；隨著嵌入層維度的增大，在Criteo 數據集APNN 模型的預測性能反而下降。其原因是Criteo 數據集的特征數量大于Avazu 數據集，導致模型優化困難。

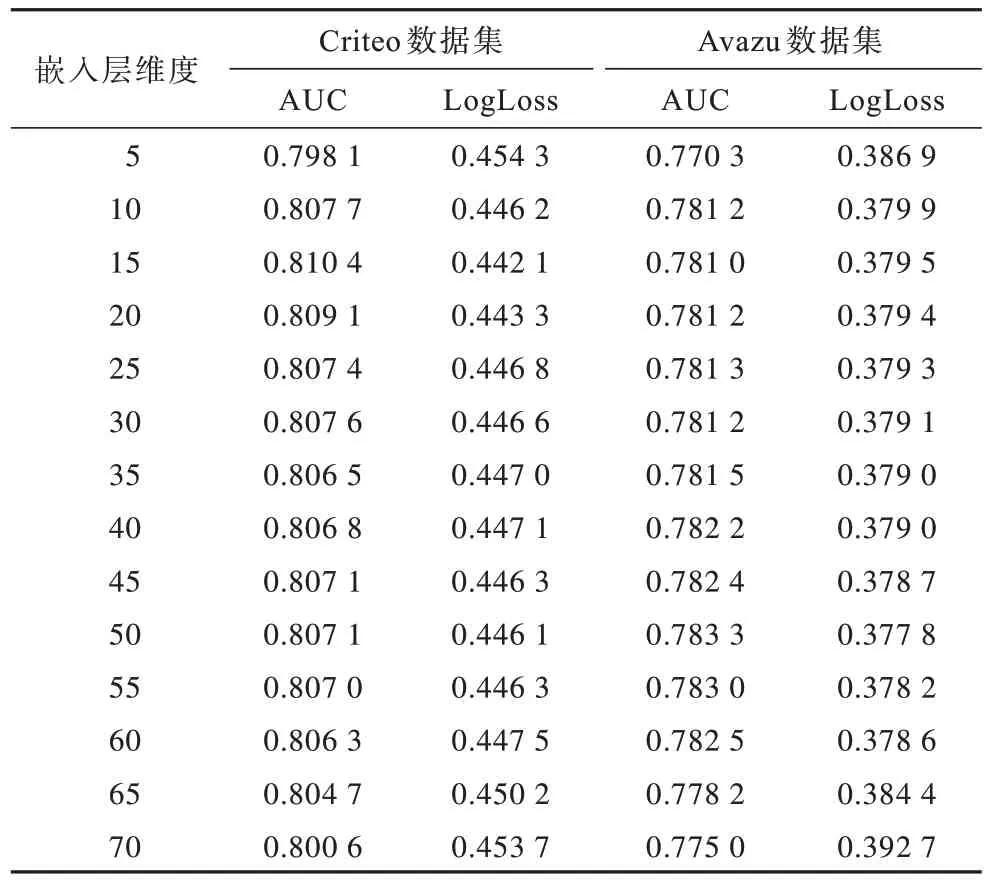
表5 嵌入層維度對APNN 模型性能的影響Table 5 Influence of embedding dimension on performance of APNN model

2）DNN 每層神經元的數量對模型預測性能影響

DNN 每層神經元的數量對預測性能影響是用于分析全連接層不同的神經單元數量對模型預測性能的影響。為簡化實驗步驟，本文統一將每個全連接層的神經元數量按如下順序設置：｛500，750，1 000，1 250，1 500，1 750，2 000，2 250，2 500｝，每層神經元數量對APNN 性能的影響如表6 所示。從表6 可以看出，每層神經元的數量增加在一定程度上可以提升模型的性能，同時提升了學習參數的復雜度，因此在訓練模型時需要考慮神經元數量。每個全連接層神經元數量剛開始逐步增加時，AUC 指標逐漸增加，LogLoss 指標逐漸降低。對于Criteo 數據集，神經元數量在1 000 時，AUC達到最優值，當逐步增加神經元數量時AUC 指標不再有明顯提升，反而會有所降低。在Avazu 數據集上的實驗結果表明，每層神經元數量的最優值設置為2 000，之后AUC 指標同樣不再明顯提升。隨著神經元數量的增多，APNN 模型可以學習到更多高階隱含信息，從而提升模型預測精度。但是當神經元數量達到一定閾值時，神經元數量對APNN 模型性能的影響已經到達極限，再增加神經元數量，模型可能學習到更多噪聲，無法提升模型性能，不僅增加了模型復雜度而且導致模型精度下降，因此需要合理選擇每層神經元數量。

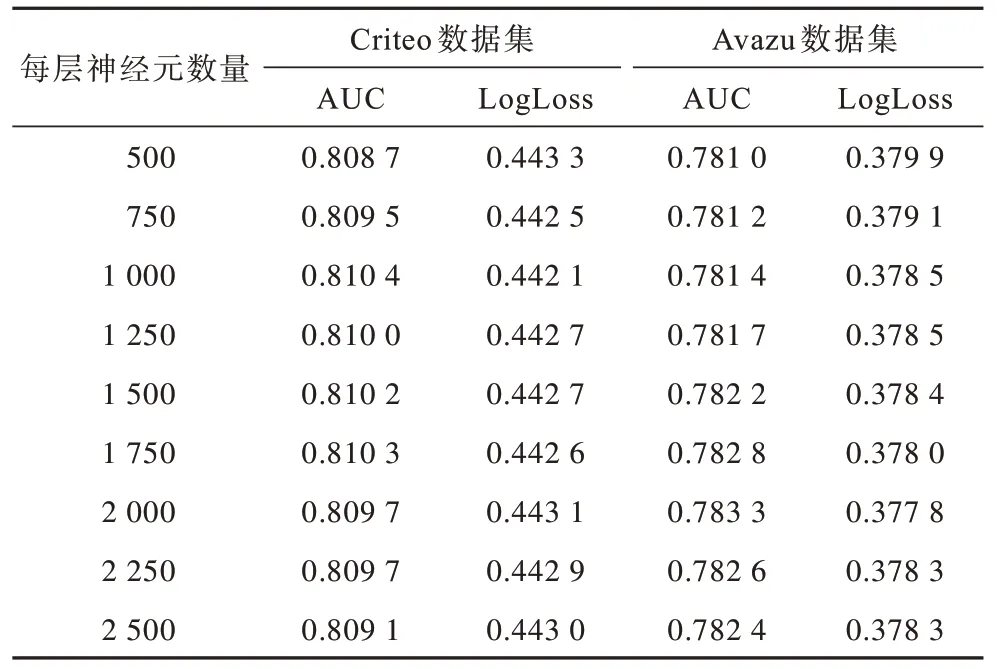
表6 每層神經元數量對APNN 模型性能的影響Table 6 Influence of the number of neurons in each layer on performance of APNN model

3）DNN 的深度對模型預測性能的影響

DNN 的深度對模型預測性能的影響是用于分析增加DNN 的全連接層數量對模型預測性能的影響。本文使用全連接層數量設置為0～7，當層數設置為0時，APNN 模型由APNN-Deep 退化為APNN-Shallow。全連接層數量對APNN模型性能的影響如表7所示。DNN層數增加也會增加模型的復雜性。從表7 可以看出，DNN 層數增加開始可以提升模型的性能，如果層數持續增加，則模型性能下降，這是因為過于復雜的模型容易過擬合。因此，全連接層的數量設置為3 是一個合理的選擇。

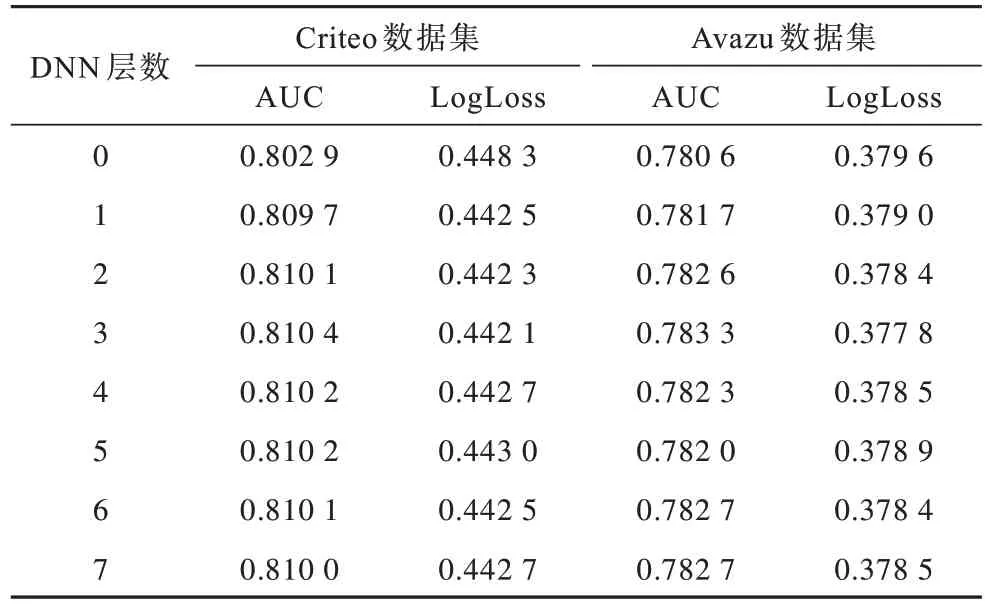
表7 全連接層數量對APNN 模型性能的影響Table 7 Influence of the number of fully connected layers on APNN model performance

3.3.5 單一結構與融合結構的模型性能對比

本文將AFM-Deep、引入一階信息重要性的LFE-PNN 與APNN 進行對比，得到融合模型性能提升的原因。不同模型的性能對比如表8 所示。從表8 可以看出，APNN 融合模型在實驗結果上高于原來的基礎算法，原因是AFM 本身是元素級特征交互，LFE-PNN 模型是向量級特征交互，融合這兩種模型的目的在于既考慮特征元素之間的交互信息，進一步使向量在各維度上充分交互，又考慮了特征向量化后的特征與特征之間的向量直接交互信息。因此，融合后的APNN 模型同時具有兩種特征級的信息表示，并且具有不同特征交互信息，能夠使DNN 挖掘出更多的高階特性交互信息表示。

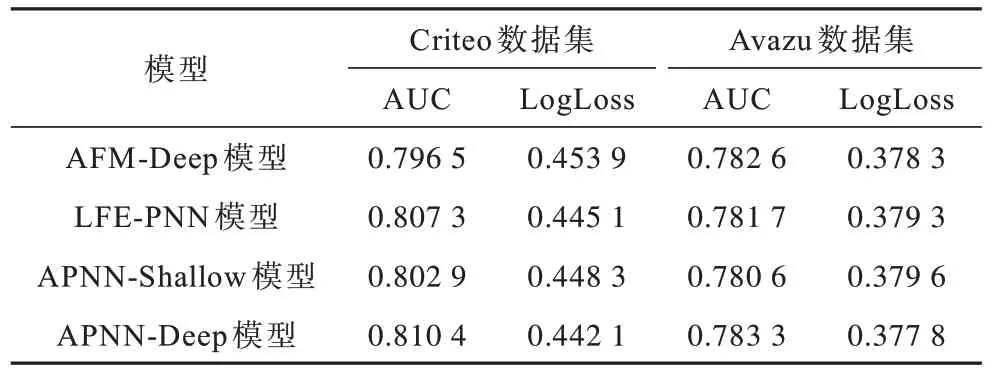
表8 在Criteo 和Avazu 數據集上不同模型的性能對比Table 8 Performance comparison among different models on Criteo and Avazu datasets

3.3.6 不同改進對APNN 模型性能的影響

盡管之前的實驗證明改進的APNN 模型對預測性能的提升，但還未將APNN中每個改進從模型中分離出以單獨研究改進對模型性能提升的貢獻。本文通過對APNN 模型進行消融實驗，實驗分為Shallow 組和Deep組，分別設置APNN-Shallow 為Shallow 組的基礎模型，APNN-Deep 為Deep 組的基礎模型。通過以下方式進行實驗：1）APNN-S-AE 模型是將注意力交互層和一階信息增強層的特征數據進行拼接后預測；2）APNN-S-AP是將注意力交互層和外積層的特征數據進行拼接后進行預測；3）LFE-PNN 模型將一階信息增強層和外積層的特征數據拼接輸入DNN得出的結果用于預測。APNN模型中不同改進的性能對比如表9 所示，如果Shallow組中APNN-S-AE 模型去掉一階信息增強層，則模型會退化為AFM 模型。如果APNN-S-AP模型刪除外積層，則同樣會退化為AFM 模型。在Deep 組中如果刪除APNN-Deep 模型的注意力交互層輸出結果，模型也會降級為LFE-PNN 模型。從表9 可以看出，引入一階信息的貢獻度比AFM 引入DNN 稍大，以實現APNN 模型的預測性能，注意力交互層、一階信息增強層和外積層都是必要的，刪除任何一部分都會導致模型預測性能明顯下降。

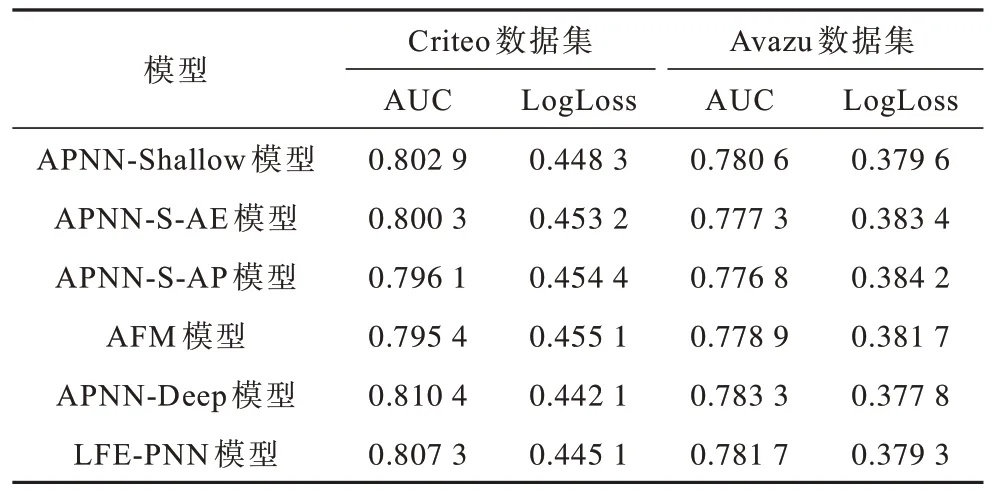
表9 APNN 模型中不同改進的性能對比Table 9 Performance comparison of APNN model with different improvements

4 結束語

為提高廣告點擊率預測效果，本文提出一種基于特征增強聚合的APNN 模型。通過結合AFM 和PNN 模型的特征提取優勢，動態地學習一階信息重要性和不同特征級信息，實現對記憶和泛化能力的平衡。在Criteo 和Avazu 數據集上的實驗結果表明，相比FNN、PNN、AFM 等模型，APNN 模型的AUC 和LogLoss 性能指標較優。后續將引入遷移學習［28］解決在線CTR 預測任務中新用戶、新廣告的冷啟動問題［29-30］，進一步提升模型性能。