基于自適應分層閾值判斷的神經網絡模型壓縮

盧 鵬，萬 瑩，鄒國良，陳金宇，鄭宗生，王振華

（上海海洋大學信息學院，上海 201306）

0 概述

卷積神經網絡（Convolutional Neural Network，CNN）是一類包含卷積計算且具有深度結構的前饋神經網絡，是深度學習的代表算法之一［1］。自深度卷積神經網絡AlexNet［2］問世并在圖像分類領域取得優異成績后，CNN 算法得到了廣泛應用［3］，如計算機視覺領域中的圖像分類、目標檢測、語義分割等。同時，在ImageNet 比賽帶來的分類挑戰影響下，CNN 技術在架構深度方面獲得重大突破［4］，優秀模型已經從8 層發展到100 層以上。此外，CNN 在人工智能、自然語言處理、故障診斷上也具有廣闊的應用前景。

面對眾多挑戰，研究者希望構建出快速并且緊湊的CNN 網絡［5-6］。常見的方法有權值修剪［7-8］、低秩擴展［9］、量化、二值化［10］、動態分解等。HAN 等首先計算出參數權重，在不影響整體精度的情況下修剪小幅度的權值，然后再次訓練。但此方法并不能同時減少計算時間和參數量，因為刪除的大部分參數屬于全連接層，其在總體浮點運算中占比很小。如在VGG16 中，全連接層參數占據總數的90%，但在總體浮點運算中只占比1%。低秩擴展通過對網絡層的分解來降低計算成本，量化、二值化、動態分解則進行快速推理，都屬于直接學習方法。然而，關于CNN 模型加速和壓縮的研究成果［11］，大多都只能單獨提升速度或存儲容量，較少有能夠同時解決這兩個問題的方法。另一個壓縮CNN 模型的方向是網絡稀疏化。稀疏化可以施加于不同層次的結構，這雖然加大了模型壓縮率，加快了推理速度，但重復次數多且需要特殊的軟件/硬件加速器來節省時間［10］。

本文在網絡正則化的基礎上，提出一種新的閾值判定方法，以去除網絡層中的冗余連接，減少分配給參數的存儲，從而減少計算成本。文獻［12］提出的網絡修剪方法使用了固定閾值，從全局進行一次網絡剪枝，而本文則提出自適應動態剪枝算法，在預剪枝階段逐層自適應地分出斷點，并采用斷點中的最小值作為閾值，針對每層不同的閾值標準進行剪裁。

1 相關工作

目前CNN 模型已經在計算機視覺領域取得了長足的進步，但是因為在一般情況下，深層網絡比淺層網絡的效果更好，所以卷積神經網絡參數巨大，并且計算卷積層和全連接層需要大量的浮點矩陣乘法，導致計算開銷也非常大，雖然有的網絡可以在GPU 上實時運行，但是如此龐大的規模使其無法直接應用于手機等移動設備中。因此，深度學習模型的壓縮成為一個亟需解決的重要問題。

目前多數CNN 網絡結構（如VGGNet、AlexNet、ResNet、DenseNet［13］等）在卷積層都會產生大量的計算成本，導致全連接層中包含大量的網絡參數。因此，很多加速壓縮研究都集中在卷積層和全連接層。

為降低計算成本，研究者提出了近似卷積運算，即將權矩陣表示為2 個較小的低秩乘積，如奇異值分解（SVD）［9］，但因為CNN 中的計算操作主要來自卷積層，所以這種方法在全連接層的作用比卷積層更大。然而，實現低秩分解通常會比較困難，因為分解過程包括計算復雜度高的分解操作。另一個問題是當前的低秩分解方法是逐層進行的，不能進行全局的參數壓縮，因為不同的網絡層具備的信息也是不同的。

在基于權值量化的方法中，文獻［14］使用8 位定點整數來代替32 位浮點數，文獻［15］提出將實值權值量化為二元/三元權值（限為｛-1，1｝或｛-1，0，1｝的權值），文獻［15］提出了量化卷積神經網絡，其量化權重并將計算轉換為卷積層中的內積。但是，二值化網絡在處理大型CNN 時會使準確率明顯下降。目前的二值化方式大多采用簡易的矩陣近似策略，忽略了二值化對最終性能造成的影響。在權重剪枝方面，文獻［12］提出用小的權值來修剪不重要的連接，通過存儲稀疏格式的模型來減少存儲空間，但這些方法需要專用的稀疏矩陣運算庫甚至硬件才能實現加速。針對結構化稀疏問題，文獻［16］提出一種結構化稀疏學習（SSL）方法來稀疏化CNN 中不同層次的結構（如過濾器、通道或層），文獻［17］在訓練時通過隨機去激活卷積層上的輸入-輸出通道連接來引入稀疏性，文獻［18］在訓練過程中施加了神經元水平的稀疏性，使一些神經元可以被修剪以獲得緊湊的網絡。上述方法都利用訓練過程中的群體稀疏化來獲得結構化稀疏性，是針對神經元或者通道而不是權重進行修剪，因此不需要太多專用庫來實現推理加速，本文所使用的精簡方法也屬于此類。此外，文獻［19］通過組合網絡修剪、加權量化和霍夫曼編碼來進一步減少存儲，文獻［20］提出動態網絡手術，參考文獻［9］的方法動態修剪和拼接連接。

雖然已有很多經典的CNN 模型［1，21-22］，但也有一些自動學習網絡架構的探索，如在給定資源預算的情況下引入網絡架構搜索的子模塊/超模塊優化［23］。還有一些研究［24］提出利用強化學習來自動學習神經結構，這些方法的搜索空間非常大，需要訓練數百個模型來區分優劣。雖然選擇僅限于每一層的寬度，但網絡剪枝也可以被視為一種架構學習方法。

目前除了對BP 神經網絡的研究外，還有針對非迭代神經網絡的研究。文獻［25］提出一種通用的幾何變換模型，遵循了訓練和自我訓練原則，為廣泛的問題提供了有效的解決方案。文獻［26］提出了一種以線性多項式作為構造公式求解多元線性回歸任務的新方法，能夠實現快速識別同時又能保證高精度。這些方法也是壓縮中的重要分支。

在上述的各類方案中，不同層級的稀疏性有不同的特點，最粗的層級在修剪時不需要特殊的包來獲得推理加速，但其靈活性較差，有時會剪掉完整的層，并且只有當深度超過50 層時，去除層才有效果。而更細致的修建方式（如權重修剪）雖然具有較高的靈活性和通用性，但卻又需要特殊的軟件和硬件進行推理［22］。相比之下，居中的通道級別的修剪及通道級稀疏，在靈活性和易于實現之間實現了良好的折衷，其可應用于經典的CNN 網絡，即將每個神經元視為一個通道。

2 自適應動態剪枝方法

本文設計一種自適應方案來實現CNN 的通道級稀疏。稀疏性在不同的層級上有不同的級別，如層級、通道級、內核級或重量級。最粗的層級稀疏不需要特殊的軟件或硬件來進行加速，但靈活性較差。最細的重量級稀疏雖然能提供最高的靈活性和通用性，卻通常需要特殊的軟件或硬件加速器。相比之下，通道級的稀疏性在靈活性和易于實現之間實現了很好的折衷，其可應用于任何典型的CNN 或全連接網絡（將每個神經元視為一個通道），得到的網絡本質上是未修剪網絡的“精簡版”，可以在傳統的CNN 平臺上進行有效推理，從而達到壓縮的目的。在本節中將介紹如何利用批歸一化（Batch Normalization，BN）層的權重，通過自適應分層閾值判斷算法來確定閾值，從而有效識別和刪除網絡中不重要的通道。剪枝過程如圖1 所示。首先將基線模型按文獻［14］的方法正則化，獲得正則化模型后，通過自適應閾值判斷對正則化后的權重進行分類，以最小值作為閾值進行剪枝，移除不重要的權重。由淺到深，直至最后一層，最后對剪枝結束的模型繼續訓練，以提高精度。

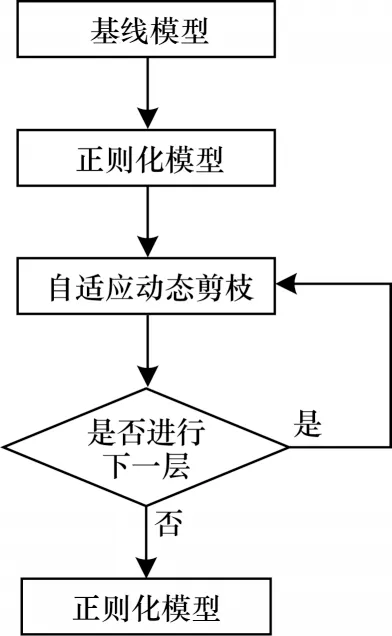
圖1 剪枝流程Fig.1 Pruning process

2.1 正則化必要性分析

在之前的工作中，基線模型進行訓練后將再次進行正則化處理，這是用一種相對比較簡單的模型來擬合復雜數據。有一些正則化可以控制神經網絡防止過擬合，如L1 正則化、L2 正則化［27］、ElasticNet回歸［28］、最大范數約束［29］、Dropout［30］等。在L1 正則化中，對每個權重w，將λ|w|添加到目標函數中，其中，λ是正則化強度；在L2 正則化中，對于網絡中的每個權重w，將1/2λw2添加到目標中，其中，λ同為正則化強度；但有時L1 回歸太過，過多特征被稀疏為0，而當L2 回歸正則化不夠，回歸系數衰減太慢時，ElasticNet 綜合回歸則會帶來更好的效果。ElasticNet 回歸綜合了L1 正則化項和L2 正則化項，其目標函數如下：

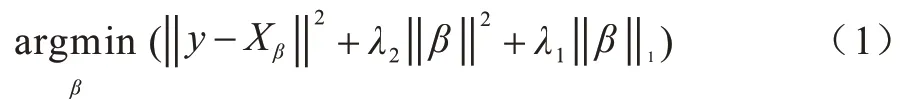
正則化后可以得到一個稀疏模型，表示只有少數特征對這個模型有貢獻，絕大部分特征是沒有貢獻的，或者貢獻微小的可以去掉，為了探究正則化后權重的作用，本文將文獻［12］中VGG16 基線模型與正則化后進行對比。如圖2 所示，正則化方法削弱了不重要的特征變量，減小了特征變量的數量級。

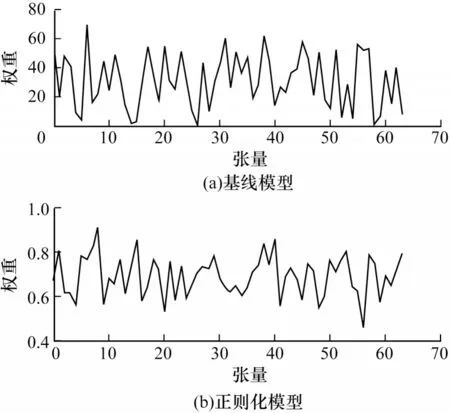
圖2 正則化前后第2 層通道權重的對比Fig.2 Comparison of channel weights of the second layer before and after regularization

通過將正則化項引入神經網絡的代價函數中，可得到輸入數據的稀疏性特征表示。稀疏性特征可以防止過擬合，提高泛化能力，更好地解釋模型。如同從生物學的角度來說，人腦中的大量神經元，當受到外界刺激（圖像或者聲音）時，只有少量的神經元被激活，大部分神經元處于抑制狀態。因此，正則化后的權重值全部減小，已有部分通道接近于0。此時再進行裁剪時，能夠得到更好的效果。表1 中數據顯示，采用文獻［12］中相同的剪枝方法，正則化前后的模型精度相近，但正則化前的剪枝率僅16%，正則化后的剪枝率可達70%，由此進一步證明了正則化的必要性。

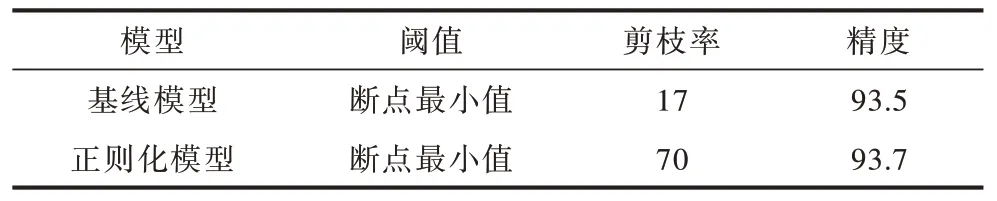
表1 正則化前后在相同閾值下的剪枝率對比Table 1 Comparison of pruning rates under the same threshold before and after regularization %

雖然正則化能夠為剪枝帶來優勢，但之前的剪枝方法中確定全局閾值需要經過大量實驗以及經驗，通過逐次比對后選取最優閾值百分比，且無法知道具體的閾值。因此，本文在前期正則化的基礎上，提出自適應分層閾值判斷算法，根據每層的權重分析對權重點進行分類，形成斷點后選取最小值，逐層修剪加權連接，這種方法可以更準確地對閾值進行判斷，在剪枝率與精度中達到最優平衡，得到更高的精度，從而更好地進行網絡模型壓縮。

2.2 分層斷點判斷

在文獻［12］關于網絡修剪的工作中，采用固定的百分比作為閾值進行全局修剪。但是如果固定百分比太高，則會導致一開始就修剪了大量連接，導致性能急劇下降。相反，如果固定百分比太低，則壓縮比可能比期望的價值小很多。因此，需要大量實驗進行經驗積累，才能確定最終閾值。為了解決這個問題，本文使用自適應分層閾值判斷算法對BN 層尺度因子進行聚類分析。在眾多散亂的尺度因子值中，自適應地找到分類簇點，再根據簇點確定最終閾值。這避免了單一的百分比方式去確定閾值，使得每層都將有其自適應的具體閾值。

按照文獻［12］中的稀疏方法，利用BN 層的縮放因子，通過聯合計算后得到每層的尺度因子，并根據這些尺度因子計算每層的閾值進行剪枝。每一層的自適應分層斷點算法描述和計算流程如下：

算法1自適應分層斷點算法

1）在每層的尺度因子中，隨機選取一個中心點X，以半徑h為內核，找出內核內的所有數據點，將這些點歸屬于一個聚類C，同時，在該聚類中記錄數據點出現的次數加1，再利用概率密度計算中心點到每個內核數據點的核密度，即加權平均值。目標函數如下：

目標函數的梯度估計如下：

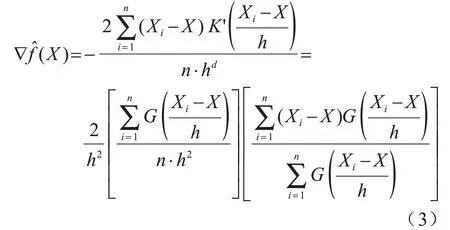
2）將這些向量相加，得到向量Mh（X），X將沿著Mh（X）的方向移動，移動距離為||Mh（X）||，即mh（X）=Mh（X）+X，然后重復迭代。在每一次迭代中，滑動窗口會移向密度較高的區域，將中心點移動到窗口內的點的平均值，滑動窗口中的密度與它內部的點的數量成比例。通過移向窗口中點的平均值，它將逐漸向更高的點密度方向移動，移動后的樣本點迭代如下：

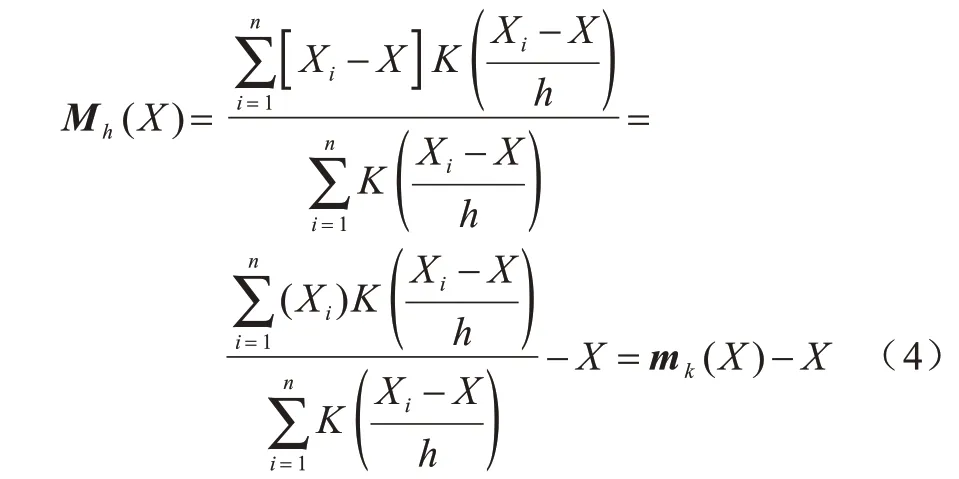
將迭代過程中遇到的點都應歸類與簇C。若收斂時當前簇C的中心與其他已存在的簇心距離過小，則會將其合并，數據點出現次數也對應合并。再次重復上述步驟直到所有點都被標記。

最后根據對每個點的訪問頻率，將訪問頻率最高的點作為斷點。實際上，每一個樣本點都需要計算其均值，并根據計算出的均值進行移動，直到滿足終止條件，最終得到的數據點也就是該點的聚類中心點。針對不同的BN 層，會自動聚類出不同的斷點。

2.3 閾值判定

在聚類出斷點后，將其由小到大進行排序，由斷點確定具體閾值。若選取的斷點數值越大，剪枝率將越高。由于權重越小，重要性越低，若選取的斷點越小，精度就將越高。因此，為了由斷點確定最優的閾值，針對不同層進行了對比實驗。如圖3 所示，在CIFAR10數據集上，假設每層均采用斷點最小值作為閾值為基礎設置，在后續實驗中，將第2 層選取倒數第二小的斷點作為閾值，其他層仍采用最小值。依次再將第3～第6 層做同樣設置可看出，若增大閾值，提高剪枝率的情況下，精度將大幅下降。并且由于第2 層的通道數為64，提高閾值后對精度的影響最大。后續3、4 層的通道數為128，5、6 層的通道數為256，其精度影響逐漸減小，但仍超出文獻［12］中最低精度，因此更加不考慮倒數第三小的斷點作為閾值，可見全局采用斷點最小值作為閾值為最佳設置。

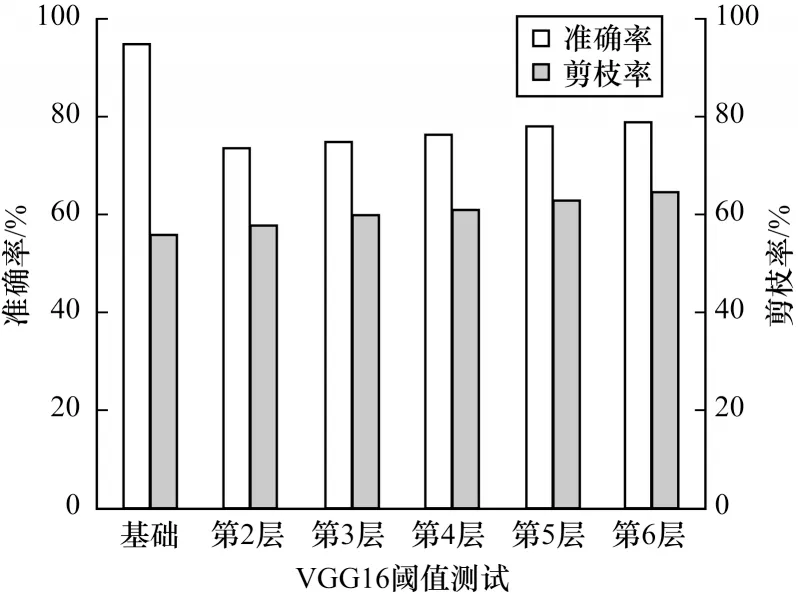
圖3 VGG16 閾值測試結果Fig.3 VGG16 threshold test result

3 實驗

本文實驗修剪了簡單的CNN 模型（VGGNet、ResNet、DenseNet）。與常用的壓縮模型AlexNet 不同，VGG 在全連接層的參數較少，因此，在這樣的網絡中修剪更具有挑戰性。在pytorch 深度學習平臺上實現了文獻［12］中的基線模型和正則化后的模型，并根據自適應分層閾值判斷結果，繼續修剪網絡中的通道。

3.1 數據集

本文實驗使用以下數據集：

1）CIFAR［31］。CIFAR 包括CIFAR-10 和CIFAR-100。CIFAR-10數據集由10個類組成，每個類包含60 000張圖像，50 000 張用于訓練，10 000 張用于測試。CIFAR-100 數據集則由100 個類組成，每個類包含600 張圖像，與CIFAR-10 不同的是，CIFAR-100 中的100 個類又被分為20 個超類，每個圖像都帶有一個“精細”標簽（它所屬的類）和一個“粗糙”標簽（它所屬的超類）。

2）SVHN。SVHN 是一個現實世界的圖像數據集，用于機器學習和識別算法。分為完整數據與裁剪數據，其中完整數據是帶有字符級邊界框的原始圖像，裁剪數據則已調整為固定的32 像素×32 像素分辨率。按照慣例，仍然使用604 388 個裁剪數據圖像進行訓練。

3）MNIST。MNIST 是一個手寫數字數據集，包含60 000 張訓練圖片和10 000 張測試圖像。為了測試本文方法在全連接網絡上的有效性，本文將與文獻［12］方法進行對比。

3.2 實驗網絡

在CIFAR 和SVHN 數據集上，實驗在3 種流行的網絡架構VGGNet、ResNet 和DenseNet 上評估本文方法。VGGNet 最初是為ImageNet 分類而設計的。在實驗中，使用包含VGGNet 的16 和19 層網絡結構和使用具有瓶頸結構（ResNet-164）的164 層預激活ResNet。對于DenseNet，使用生長速率為12（DenseNet-40）的40 層DenseNet。在MNIST 數據集上，在與文獻［12］相同的三層全連接網絡上評估本文方法。

3.3 訓練、剪枝與微調

訓練、剪枝與微調過程如下：

1）基線訓練。首先從零開始訓練所有網絡，作為基線網絡數據進行對比。所有網絡都使用SGD（Stochastic Gradient Descent）。在CIFAR 數據集上進行160 個epoch 的訓練，在SVHN 數據集上進行20 個epoch 的訓練，2 個數據集批量大小同為64，學習率同為0.1。在MNIST 數據集上進行30 個epoch的訓練，批量大小為256，初始學習率為0.1，經過20 個epoch 后初始學習率為10。為了更好地對比閾值選定對精度結果和剪枝率的影響，本文方法參數設置與文獻［12］方法保持一致。

2）稀疏訓練。在稀疏化訓練時仍沿用文獻［12］方法，為每個通道引入比例因子。聯合訓練網絡權值與比例因子，對比例因子施加稀疏正則化后得到稀疏模型。

3）剪枝。針對稀疏以后的模型進行剪枝，需要確定剪枝閾值。在文獻［12］中采用統一全局閾值一次修剪，且閾值定義為所有比例因子值的某個百分比。缺點是由于不同層數的參數量不同，重要性也不同，全局閾值需要多次反復實驗，最終確定具體閾值，且增加1%或者降低1%剪枝比例對最終精度結果影響不大，因此閾值的判斷僅靠人為選擇。而本文將針對不同層，使用自適應動態剪裁算法，自動確定不同層的具體閾值，而非百分比在精度與剪枝率取得平衡。這使得其能更好地進行裁剪，選取適合該層的閾值，而無需多次反復實驗。

4）微調。在剪枝后，將得到一個更窄、更緊湊的模型，實驗將繼續對模型微調，在CIFAR、SVHN 和MNIST 數據集上，使用與基線訓練中相同的數據設置，再次訓練，以取得更好的精度效果。

3.4 結果對比與分析

在以往的經驗中，第1 個卷積層在原始圖像的提取特征中起著重要作用，只存在較低的計算成本和較小的參數存儲（小于整個網絡的1%）。因此，在本文實驗中不修改該層的參數。同時網絡的全連接層不包含BN 層，同樣不進行修剪。

以VGG16 網絡為例，圖4 給出了剪枝層的斷點數。網絡層越深，通道的權重值增多，斷點數也逐步振蕩增加，但每層仍以斷點最小值為剪枝閾值。圖5對比了剪枝前后通道數，可以看出層數越深剪枝幅度越大，通常在更深的網絡層具有的激活映射更小，占用的內存也更少，因此會有更多的通道被修剪。

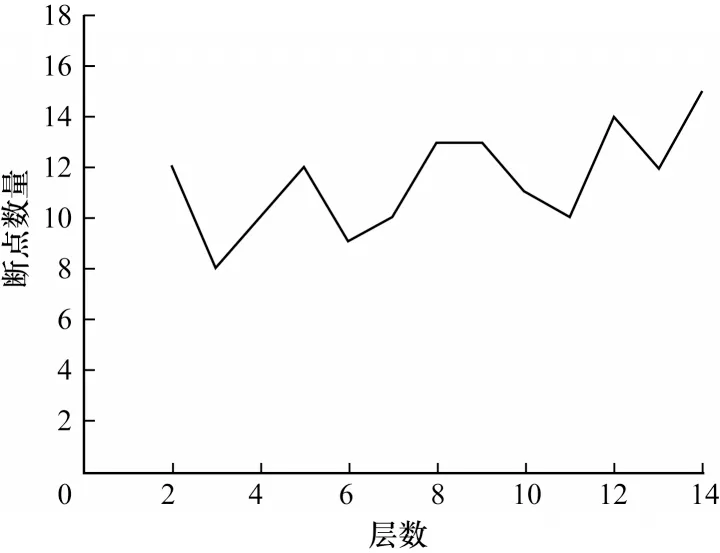
圖4 VGG16 分層斷點數Fig.4 Number of VGG16 layered break points

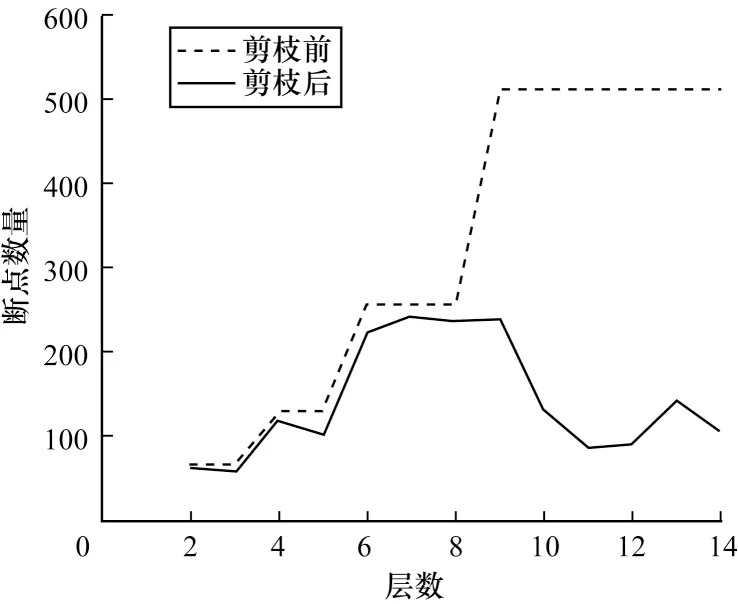
圖5 VGG16 分層剪枝通道數Fig.5 Number of VGG16 layered pruning channels

本文給出了VGG 網絡在數據集上的測試結果，為了更好地進行效果對比，以剪枝前的參數作為基線，將文獻［12］方法的剪枝率、測試錯誤率和參數量與本文方法進行對比，如表2～表4 所示。可以看出，本文不必依靠大量實驗或者以往經驗確定閾值，而是使用自適應分層閾值判斷算法可以自適應地根據斷點選擇閾值進行分層剪枝，可以保持甚至提高至更好的精度。

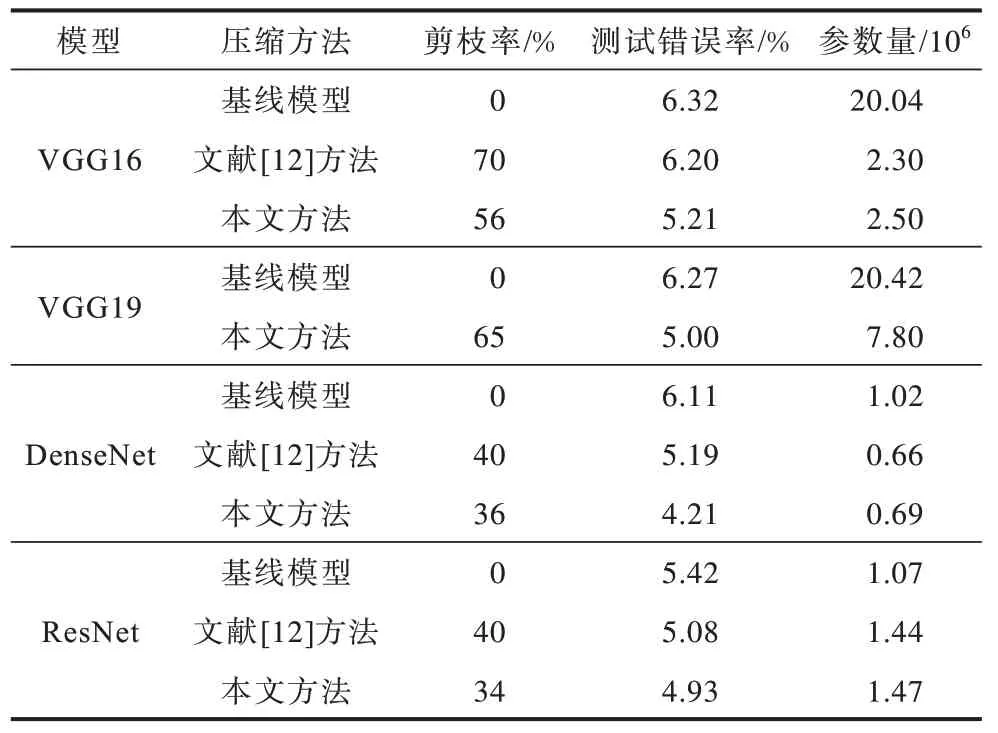
表2 CIFAR10 數據集測試結果Table 2 Test result in CIFAR10 data set

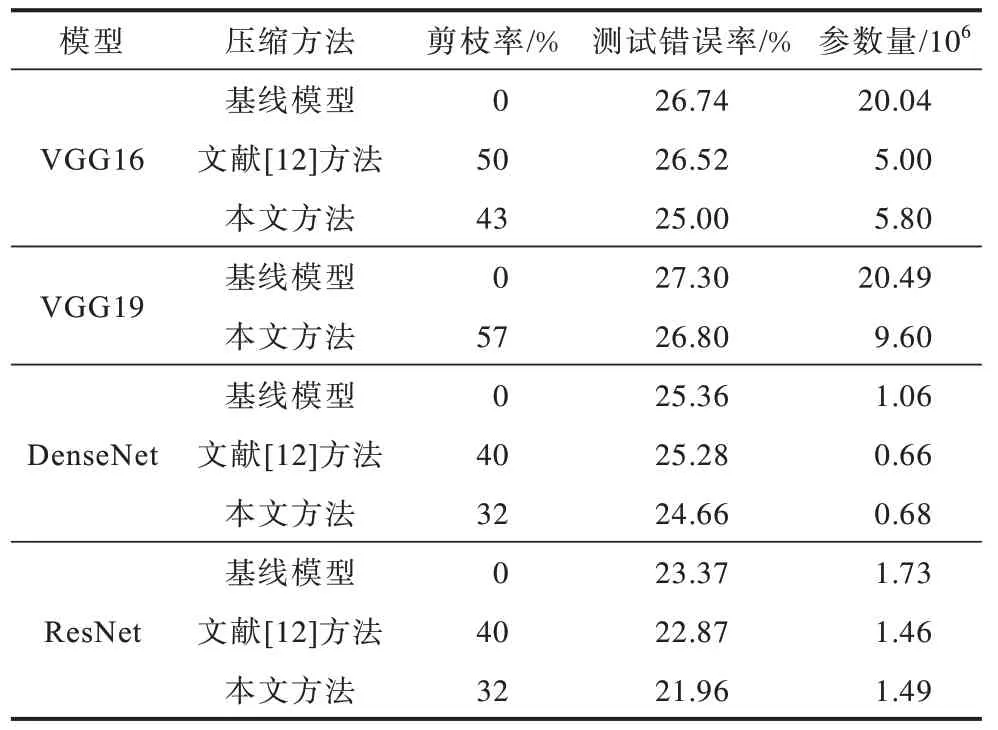
表3 CIFAR100 數據集測試結果Table 3 Test result in CIFAR100 data set

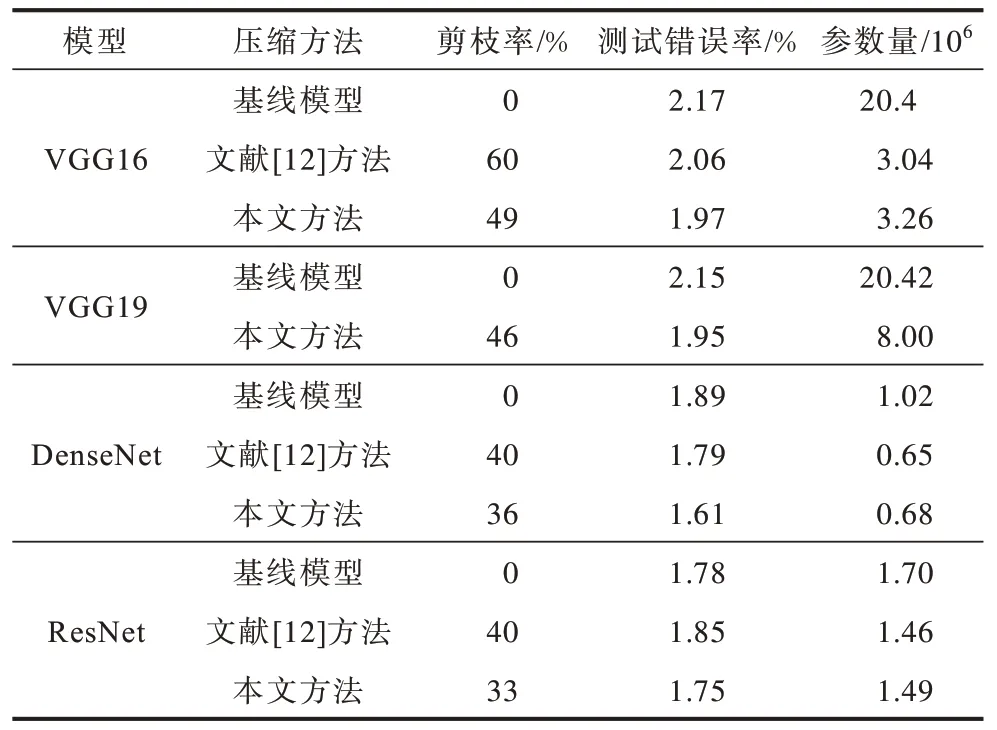
表4 SVHN 數據集測試結果Table 4 Test result in SVHN data set

CIFAR10 數據集上的實驗結果顯示：在使用本文方法情況下，對VGG16 網絡模型剪枝率為56%，測試錯誤率較使用文獻［12］方法降低1.01 個百分點；對DenseNet 網絡模型剪枝率為36%，測試錯誤率較使用文獻［12］方法降低0.98 個百分點；對ResNet網絡模型剪枝率為32%，測試錯誤率較使用文獻［12］方法降低0.15 個百分點。

在CIFAR100 數據集上的實驗結果顯示：在使用本文方法情況下，對VGG16 網絡模型剪枝率為43%，測試錯誤率較使用文獻［12］方法降低1.52 個百分點；對DenseNet 網絡模型剪枝率較使用文獻［12］方法增加8%，測試錯誤率降低0.62 個百分點；對ResNet 網絡模型剪枝率為32%，測試錯誤率較使用文獻［12］方法降低0.91 個百分點。

在SVHN 數據集上的實驗結果顯示：在使用本文方法情況下，VGG16 網絡模型相較于文獻［12］方法犧牲了11%的剪枝率和0.21×106的模型參數量，降低測試錯誤率0.09 個百分點；對DenseNet 剪枝率較使用文獻［12］方法下降4%，測試錯誤率降低0.02 個百分點，模型參數量增加0.03%；ResNet 網絡模型剪枝率為33%，測試錯誤率較使用文獻［12］方法降低0.1 個百分點。

由此可以看出，本文方法能夠降低錯誤率，調節精度與剪枝率的平衡。雖然剪枝率沒有超過文獻［12］方法，但本文方法可以更好地在剪枝與精度中找到最優平衡。表3 結果顯示，在同樣的數據集上，網絡層越深效果更好，同時剪枝率也會相應提高。

針對LeNet 網絡模型，本文在MNIST 數據集上進行了測試并與文獻［12］全局剪枝方法進行了比較，測試結果如表5 所示，其中測試錯誤率降低0.05 個百分點，參數剪枝率達到82.8%。盡管正則化的作用主要用于對卷積層中的通道進行剪枝，但它也適用于對全連接層中的神經元進行剪枝。文獻［12］中使用全局閾值修剪時有時會剪去整個層，而本文自適應分層閾值判斷算法則避免了這個問題，并獲得了略低的測試誤差。

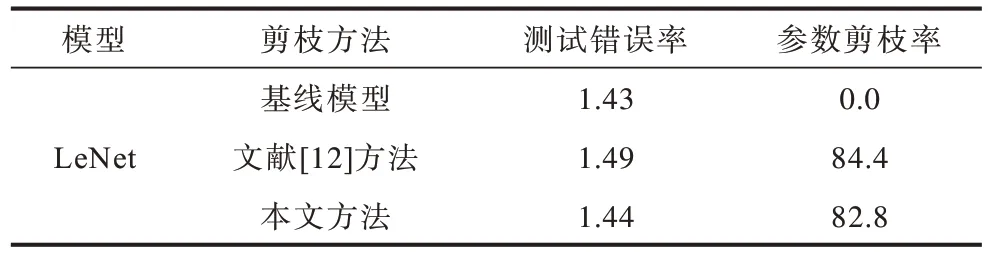
表5 MNIST 測試結果 %

4 結束語

目前，深度學習已經在圖像、文本、音頻、視頻等諸多領域取得了巨大成功，同時也推動了很多相關智能產品的誕生。CNN 網絡模型雖然結構越深效果越好，但是高容量、高訓練成本和推理成本都會影響計算效率。本文提出的自適應分層閾值判斷算法，針對正則化后的模型進行剪枝，逐層對通道權重進行斷點分層后，選取最小值為閾值進行剪枝，擺脫了以往需要經驗人為定義的固定閾值，進而獲得更加緊湊的卷積神經網絡，基于該算法可減少模型尺寸，且得到的模型不需要特殊的庫/硬件來進行有效的推理。在多個數據集上的實驗結果證明，本文方法可以減小模型尺寸且精度并沒有顯著損失。未來將研究多種壓縮方法相結合的方法，以獲得更好的壓縮結果。