GRAPES 動力框架中大規(guī)模稀疏線性系統(tǒng)并行求解及優(yōu)化

張 琨，賈金芳，嚴文昕，黃建強，2，王曉英

（1.青海大學計算機技術(shù)與應(yīng)用系，西寧 810016；2.清華大學計算機科學與技術(shù)系，北京 100084）

0 概述

全球區(qū)域同化預(yù)報系統(tǒng)（Global and Regional Assimilation Prediction System，GRAPES）是我國自主研發(fā)的新一代數(shù)值天氣預(yù)報系統(tǒng)，能夠改善天氣預(yù)報模式的性能并有效提高天氣預(yù)報精度。GRAPES 動力框架的計算核心是赫姆霍茲方程的求解，該方程是原始大氣方程組經(jīng)過一系列離散化處理之后形成的大規(guī)模稀疏線性方程組。目前對線性方程組的求解方法主要有直接法和迭代法［1-2］兩種。由于計算機硬件資源的限制，使用直接法并不能完成有效求解，而迭代法具有硬件存儲空間要求較小、原始矩陣在計算過程中保持不變等優(yōu)點。因此，目前求解大規(guī)模稀疏線性方程組主要選擇迭代法。

GRAPES 數(shù)值天氣預(yù)報系統(tǒng)采用的迭代法為廣義共軛余差（Generalized Conjugate Residual，GCR）法。文獻［3］利用基準測試程序?qū)RAPES 并行應(yīng)用進行分析，發(fā)現(xiàn)在迭代法計算過程中全局通信對整個系統(tǒng)的性能影響較大，指出在進行性能優(yōu)化時需要考慮系統(tǒng)通信所帶來的性能下降問題。文獻［4］針對赫姆霍茲方程求解過程中通信占比高的現(xiàn)象，引入短向量計算替代長向量計算，以減少通信開銷。文獻［5］在使用重啟動和截斷兩種方式進行性能優(yōu)化的同時，還使用一種新的稀疏近似逆預(yù)條件子來加快算法收斂速度。

研究發(fā)現(xiàn)，增加重啟動和截斷處理的廣義共軛余差法能夠減少數(shù)據(jù)存儲量，同時改善計算的局部性。文獻［6］為改善GRAPES 模式動力框架中存在的極點問題，利用陰陽網(wǎng)格設(shè)計新的動力框架，與原GRAPES 模式框架相比，新的動力框架表現(xiàn)出較好的數(shù)值穩(wěn)定性及計算性能。文獻［7］利用MPI 和OpenMP 混合并行的方式提升GRAPES 模式的并行度，以適應(yīng)主流硬件架構(gòu)既有分布式內(nèi)存又有共享內(nèi)存的情況。文獻［8］結(jié)合國產(chǎn)高性能平臺實現(xiàn)了基于MPI+共享變量編程模型的眾核線程級并行的多級并行方案，提升了方程求解的運行效率。文獻［9］基于PETSc 科學計算庫和Hypre 預(yù)條件庫實現(xiàn)了廣義最小殘差（Generalized Minimal Residual，GMRES）法，與GRAPES 模式現(xiàn)有的GCR 算法相比，GMRES 算法在更高分辨率的條件下具有較好的性能。文獻［10］則利用CPU 設(shè)備結(jié)合線程級并行、矢量化和數(shù)據(jù)重用技術(shù)提升了算法計算性能。當前GRAPES 模式動力框架中廣義共軛余差法的優(yōu)化工作主要集中在通用CPU 及國產(chǎn)高性能機器領(lǐng)域，部分學者討論了算法本身的改進方案，但大多是與CPU 設(shè)備進行兼容，而結(jié)合GPU 的性能優(yōu)化相對較少［11］。

本文針對GRAPES 數(shù)值天氣預(yù)報系統(tǒng)中的赫姆霍茲方程求解問題，分別通過MPI、MPI+OpenMP、CUDA 三種并行方式實現(xiàn)求解大規(guī)模稀疏線性方程組的廣義共軛余差法，并對測試結(jié)果進行對比分析，評估優(yōu)化性能。

1 GRAPES模式中大規(guī)模稀疏線性方程組求解

GRAPES 數(shù)值天氣預(yù)報系統(tǒng)主要包括動力框架和物理過程參數(shù)化方案兩部分［12-13］，其中動力框架為核心部分，將動力框架方程組進行簡化和離散后可得到GRAPES 模式的基本預(yù)報方程［14-16］。對該方程進行處理后，動力框架的主要計算內(nèi)容就變成對一個包含大型稀疏矩陣的赫姆霍茲方程的求解［17-19］。如圖1 所示，赫姆霍茲方程的求解過程計算量龐大，占據(jù)整個過程求解計算量的30%以上。隨著模式分辨率的提高，方程的計算量還會增加。因此，對赫姆霍茲方程進行高效求解成為動力框架性能提升的關(guān)鍵［20］。

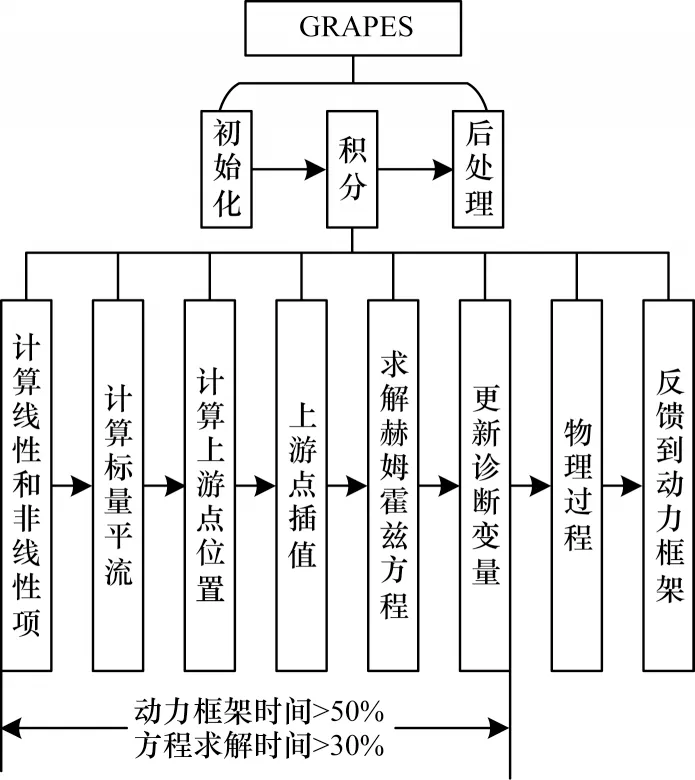
圖1 GRAPES 模式核心計算Fig.1 GRAPES core computing

如圖2 所示，GRAPES 模式動力框架部分的赫姆霍茲方程中計算每一個格點的方程需要選取空間中與其相關(guān)的19 個格點作為系數(shù)［21］。

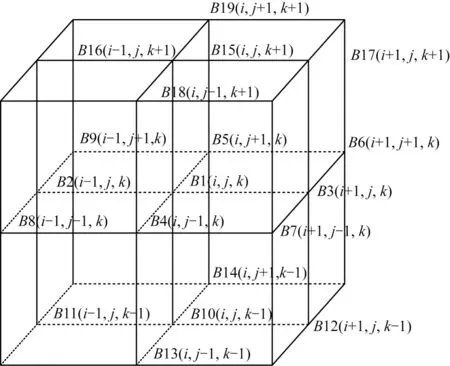
圖2 赫姆霍茲方程系數(shù)空間分布Fig.2 Spatial distribution of the coefficients of Helmholtz equation

空間格點的計算公式如下：

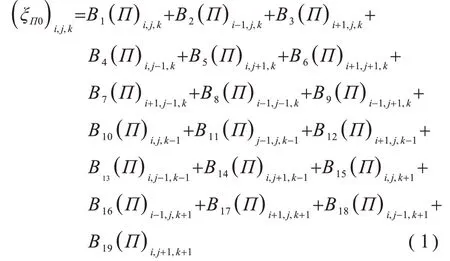
將每一個空間格點的計算進行組合后可以得到一個大規(guī)模的稀疏線性方程組，該方程組可簡化為：

其中：A是一個大規(guī)模稀疏矩陣；x是規(guī)模為空間總格點數(shù)的解向量；b是與x相對應(yīng)的方程右端向量。因此，GRAPES 模式動力框架中赫姆霍茲方程的求解就是對一個大規(guī)模稀疏線性方程組的求解。在當前系統(tǒng)中，方程求解所采用的算法為廣義共軛余差法，在滿足精度要求的前提下，廣義共軛余差法算法收斂較快，整體算法易于實現(xiàn)，綜合表現(xiàn)較好［22］。廣義共軛余差法的具體內(nèi)容如算法1 所示。

算法1廣義共軛余差法

2 廣義共軛余差法的并行實現(xiàn)

2.1 問題模型

本文主要考慮問題模型Ax=b，等式中的A為稀疏矩陣，x為需要求解的向量，b為右端向量。系數(shù)矩陣具有明顯的稀疏性，在矩陣存儲格式的選擇上，統(tǒng)一使用CSR（Compressed Sparse Row）格式［23-24］。方程求解算法選擇廣義共軛余差法，算法主要計算內(nèi)容包括稀疏矩陣向量乘、向量內(nèi)積、向量數(shù)乘。

2.2 系數(shù)矩陣預(yù)處理優(yōu)化

迭代法具有依賴系數(shù)矩陣條件數(shù)的特點，可能存在收斂速度慢甚至不收斂的情況，因此，通常使用預(yù)處理技術(shù)對算法進行優(yōu)化。目前的預(yù)處理技術(shù)主要通過構(gòu)建預(yù)條件子將原方程Ax=b轉(zhuǎn)化為M(-1)Ax=M(-1)b等形式求解。常用的預(yù)條件子構(gòu)造方法有稀疏近似逆預(yù)條件、不完全分解預(yù)條件等。本實驗所采用的預(yù)條件技術(shù)為不完全分解LU 預(yù)條件子（ILU）。預(yù)處理過程將原始矩陣A分為上三角矩陣U、下三角矩陣L及殘差矩陣R，分解之后的矩陣可以滿足不同條件P，例如與原系數(shù)矩陣的稀疏結(jié)構(gòu)保持一致。構(gòu)造ILU 預(yù)條件子的過程如算法2 所示。

算法2ILU 分解

2.3 MPI 并行及MPI+OpenMP 混合并行

通信開銷是MPI 程序中不可忽視的部分，尤其是隨著進程規(guī)模的增大，在計算時間減少的同時也會增加程序的通信開銷［25-26］。因此，在設(shè)計MPI 并行算法時，需要平衡計算任務(wù)劃分與通信函數(shù)使用之間的關(guān)系。在廣義共軛余差法中，每一個迭代步驟之間都存在數(shù)據(jù)依賴，并行任務(wù)主要選擇在每一個迭代步驟內(nèi)部進行。MPI 并行方式將計算任務(wù)根據(jù)分配的進程數(shù)量進行劃分，每個進程處理不同的子任務(wù)，最后利用進程間通信進行數(shù)據(jù)同步。

本文實驗所測試的MPI+OpenMP 混合并行方式，在MPI 并行方式的基礎(chǔ)上，利用多線程實現(xiàn)了更細粒度的任務(wù)劃分。OpenMP 是共享內(nèi)存并行編程模式，與MPI 并行模式相比可減少數(shù)據(jù)通信的時間。在矩陣向量乘部分的并行處理中，MPI+OpenMP 混合并行任務(wù)劃分如圖3 所示。矩陣數(shù)據(jù)按行子域劃分為不同的row_part，每個MPI 進程只計算所屬row_part 與向量的乘積，各進程并行執(zhí)行計算任務(wù)。同時在MPI 進程內(nèi)部利用OpenMP 模式將row_part劃分為更細粒度的subrow_part，結(jié)合線程級并行完成子任務(wù)計算。

圖3 MPI+OpenMP 混合并行結(jié)構(gòu)Fig.3 MPI+OpenMP hybrid parallel structure

2.4 GPU 并行優(yōu)化

2.4.1 數(shù)據(jù)傳輸優(yōu)化

利用CUDA并行求解方程時主要開銷在于GPU與CPU 之間的數(shù)據(jù)傳輸，為減少數(shù)據(jù)傳輸時間開銷，避免PCI-E 總線上的數(shù)據(jù)傳輸成為程序性能提升的瓶頸，將矩陣A以及各個中間向量等都保存在GPU 上。在計算過程中利用顯存進行通信，避免和主機端進行頻繁的數(shù)據(jù)傳輸。無法避免的數(shù)據(jù)傳輸過程只出現(xiàn)在需要進行收斂判斷及主機端計算的情況下，同時在數(shù)據(jù)傳輸時采用頁鎖定內(nèi)存（pinned memory）進一步提高數(shù)據(jù)傳輸速度。如圖4 所示，與可分頁內(nèi)存（pageable memory）相比，頁鎖定內(nèi)存能夠減少一次數(shù)據(jù)傳輸操作，提高數(shù)據(jù)傳輸效率。

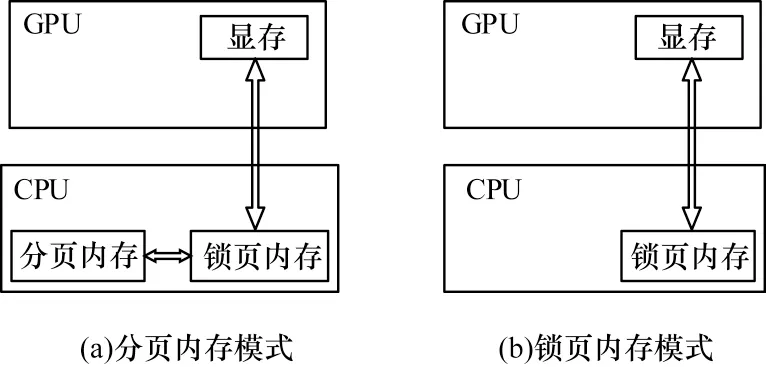
圖4 內(nèi)存模式對比Fig.4 Comparison of memory modes

2.4.2 訪存優(yōu)化

GPU 對全局存儲器的訪問速度也會對程序性能造成一定影響，利用CUDA 模型可以實現(xiàn)線程塊間及線程塊內(nèi)兩級并行，從而完成對全局存儲器的合并訪問。初始的數(shù)據(jù)存儲格式由于將需要連續(xù)訪問的數(shù)據(jù)離散存儲，不滿足線程合并訪問的條件，因此需要對數(shù)據(jù)存儲格式進行轉(zhuǎn)換。將三維格式的矩陣轉(zhuǎn)化為一維格式存儲之后，每一個網(wǎng)格點在計算過程中同一線程束內(nèi)的線程所訪問的內(nèi)存空間是連續(xù)的，滿足合并訪存的要求。如圖5 所示，當同一線程束內(nèi)的線程訪存連續(xù)時，能夠?qū)⒍啻卧L存操作減少為一次訪存操作，從而減少計算過程中的訪存開銷。

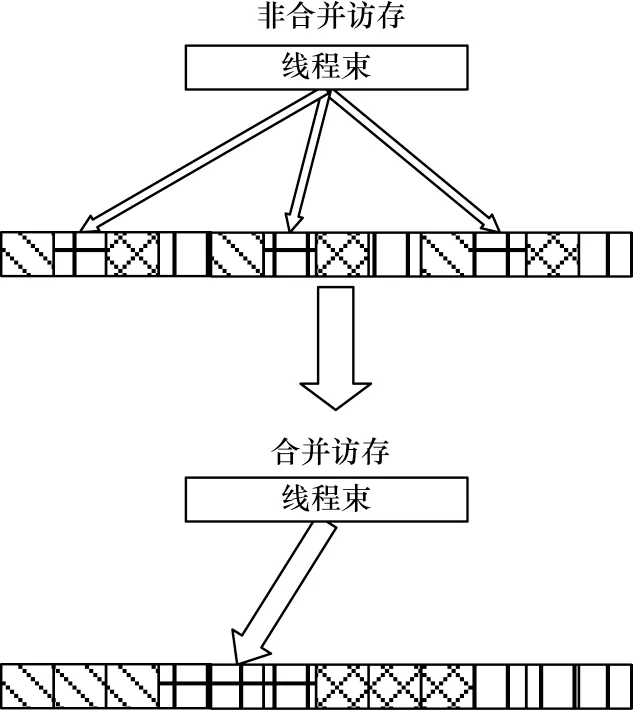
圖5 合并訪存Fig.5 Coalesced access

2.4.3 存儲器優(yōu)化

在GPU 計算過程中，存在一部分數(shù)據(jù)只需要線程塊內(nèi)部的線程訪問。對于這一部分數(shù)據(jù)，利用共享存儲器進行保存。共享存儲器的訪問延遲比全局存儲器低，在計算過程中線程塊內(nèi)部的線程只需要訪問共享存儲器中，而不需要去訪問全局存儲器，從而進一步提高訪存的速度。

在向量內(nèi)積的計算過程中，并行方式如圖6 所示。內(nèi)積計算過程可以表示成形式，向量a和向量b分別對應(yīng)圖中Vector a 和Vector b。當核函數(shù)啟動后，將向量子任務(wù)subVector 分配到不同的線程塊中。由于向量內(nèi)積涉及到對同一內(nèi)存地址的修改操作，因此先利用線程塊訪問各自私有的共享存儲器進行局部規(guī)約操作，這一部分計算內(nèi)容可以并行執(zhí)行。當所有subVector 都完成局部歸約后，再進行最后的規(guī)約操作，從而提高整體的計算速度。

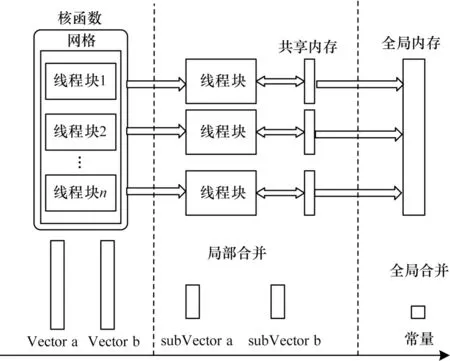
圖6 CUDA 內(nèi)積并行結(jié)構(gòu)Fig.6 CUDA dot parallel structure

3 實驗與分析

3.1 實驗環(huán)境及測試數(shù)據(jù)

實驗中共使用5 個CPU 節(jié)點，節(jié)點處理器為Intel?Xeon?CPU E5-2692 v2 @ 2.20 GHz。每個節(jié)點兩塊CPU（共24 核心），節(jié)點內(nèi)存為64 GB；實驗使用GPU 為Tesla T4，顯存容量為16 GB；CUDA 版本為v10.1。實驗所使用的測試數(shù)據(jù)包含系數(shù)矩陣A、初始解x0、右端向量b，其中系數(shù)矩陣A規(guī)模為360×180×38，共2 462 400 個網(wǎng)格點。

3.2 結(jié)果分析

實驗測試了數(shù)據(jù)在不同計算方式下的計算殘差。結(jié)果表明，使用3 種并行方式實現(xiàn)的廣義共軛余差法與串行方式能夠得到一致的計算結(jié)果，驗證了不同并行方式求解稀疏線性方程組的正確性和有效性。

3.2.1 預(yù)處理優(yōu)化結(jié)果

對原始GCR 算法進行預(yù)處理優(yōu)化后，方程的收斂速度獲得大幅提升。如圖7 所示，在誤差精度要求為1E-10 的條件下，預(yù)處理算法收斂所需的迭代次數(shù)從134 次下降至21 次。ILU 預(yù)處理的引入能夠改善方程的求解性能，同時也會增加新的計算內(nèi)容。但是在并行算法中，計算量已經(jīng)不是限制性能的最大因素，例如在MPI 程序中，隨著并行度的增加，進程之間的通信成為限制程序性能的最大因素。在利用MPI 實現(xiàn)的并行GCR 算法中，每一次迭代過程都會進行數(shù)據(jù)通信，所以，利用預(yù)處理技術(shù)加快算法收斂速度之后，整體的計算性能可以獲得提升。

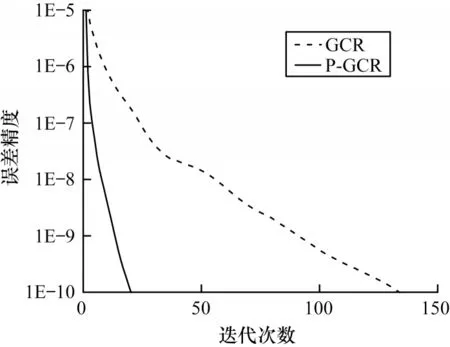
圖7 預(yù)處理優(yōu)化對計算性能的影響Fig.7 Effect of preprocessing optimization on computational performance

3.2.2 MPI 并行結(jié)果

雖然使用MPI 并行方式能夠通過提高進程數(shù)目減少子任務(wù)的計算量，從而有效提升計算部分速度，但是也會增加數(shù)據(jù)通信的時間開銷。MPI 并行算法在實現(xiàn)過程中避免了冗余的通信開銷，只對部分必要的向量更新操作進行通信。MPI 并行算法在不同進程規(guī)模下的運行時間如圖8 所示。可以看出，隨著進程規(guī)模的增加，運行時間呈先下降后上升的趨勢。這是因為MPI 算法的進程數(shù)量會影響進程之間的通信開銷，當進程數(shù)為32 時，并行計算任務(wù)所帶來的性能提升不足以抵消增加的通信開銷，程序整體性能就會下降。由于MPI 并行方式存在可擴展性問題，因此只通過增加進程數(shù)量的方式來提高性能并不能高效地利用計算資源。

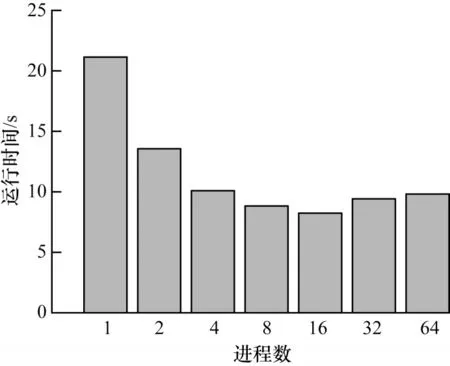
圖8 MPI 運行時間Fig.8 Runtime of MPI

3.2.3 MPI+OpenMP 混合并行結(jié)果

與MPI 并行方式相比，MPI+OpenMP 混合并行方式充分結(jié)合了共享內(nèi)存的優(yōu)勢，在不改變原始MPI 并行方式粗粒度通信的情況下，提高了進程內(nèi)部的線程級并行度。圖9為MPI并行與MPI+OpenMP混合并行在不同核數(shù)規(guī)模下的計算性能對比。可以看出，當計算所使用的核數(shù)過少時，利用OpenMP 進行更細粒度的并行劃分之后性能并沒有明顯改善，但隨著核數(shù)的增加，OpenMP 的共享內(nèi)存優(yōu)勢得以發(fā)揮，計算性能相比MPI 并行方式有一定提升。當核數(shù)為64 時，MPI 并行方式已經(jīng)出現(xiàn)性能下降，但是MPI+OpenMP 混合并行方式的性能依然較穩(wěn)定。因此，在MPI 并行方式由于可擴展性原因造成計算效率下降的情況下，使用MPI+OpenMP 混合并行方式可以獲得更好的性能。

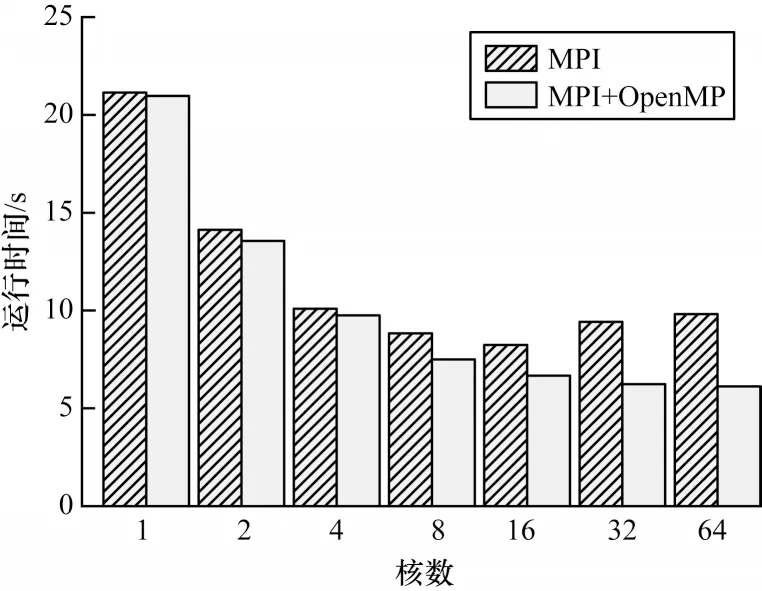
圖9 MPI 與MPI+OpenMP 運行時間對比Fig.9 Runtime comparison between MPI and MPI+OpenMP

3.2.4 GPU 并行結(jié)果

基于GPU 的CUDA 并行方式在優(yōu)化措施上采用了共享存儲器優(yōu)化、全局存儲器訪存優(yōu)化以及主從設(shè)備數(shù)據(jù)傳輸優(yōu)化。CUDA 并行與MPI+OpenMP混合并行在算法求解過程中主要步驟的性能對比如圖10 所示。與MPI+OpenMP 混合并行相比，CUDA并行在矩陣向量乘部分（ar）有32%的性能提升，向量數(shù)乘部分（p&ap，x&r）有88%的性能提升，向量內(nèi)積部分（beta，alpha，residual）有80%的性能提升。

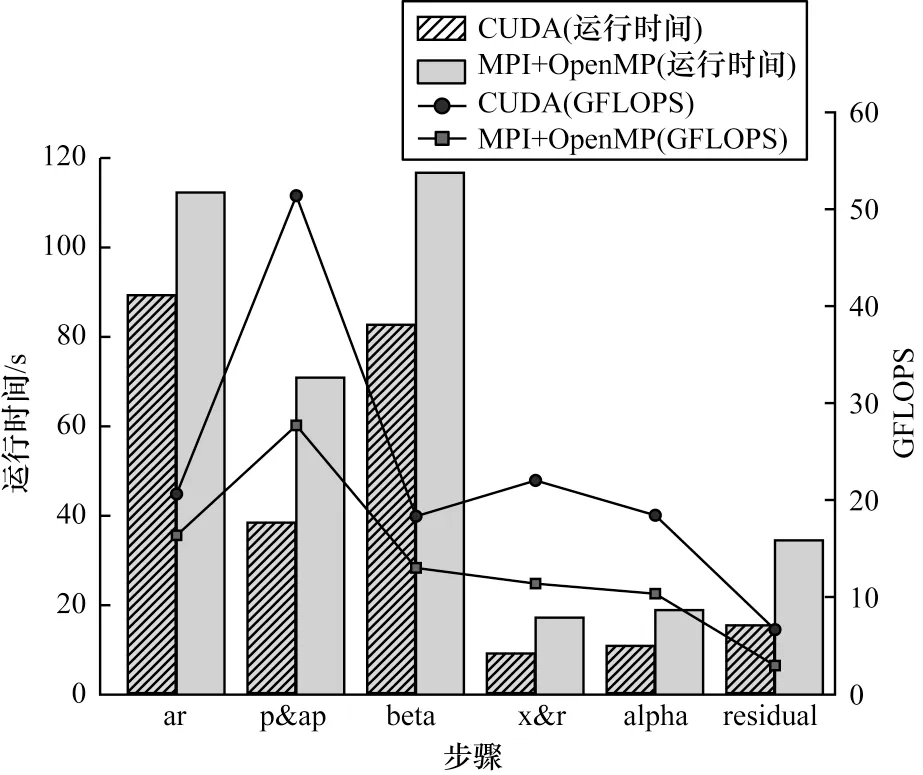
圖10 CUDA 與MPI+OpenMP 主要步驟計算性能對比Fig.10 Performance comparison of main steps of CUDA and MPI+OpenMP

3.2.5 優(yōu)化性能對比

對不同優(yōu)化方式的優(yōu)化性能進行對比，結(jié)果如圖11 所示。可以看出，通過預(yù)處理優(yōu)化減少算法迭代次數(shù)對整體計算性能提升明顯，加速比達到4.5。在預(yù)處理的基礎(chǔ)上，使用MPI 并行方式的性能獲得提升，加速比達到11.7。結(jié)合OpenMP 并行方式進行細粒度任務(wù)劃分之后，混合并行計算性能相對于MPI 并行方式有一定提升，加速比達到15.8。同時數(shù)據(jù)也顯示CUDA 并行方式相對于MPI+OpenMP混合并行方式能夠獲得約50%的性能提升，加速比達到23.4。基于GPU 的并行方式在計算時間上的開銷遠小于基于CPU 的并行方式，這得益于GPU 數(shù)量眾多的計算核心。在數(shù)據(jù)通信方面，GPU 并行方式線程級的通信相比于CPU 并行方式也具有優(yōu)勢，不需要進行各個進程之間的數(shù)據(jù)通信，所以基于GPU的CUDA 并行方式能獲得較好的計算性能。

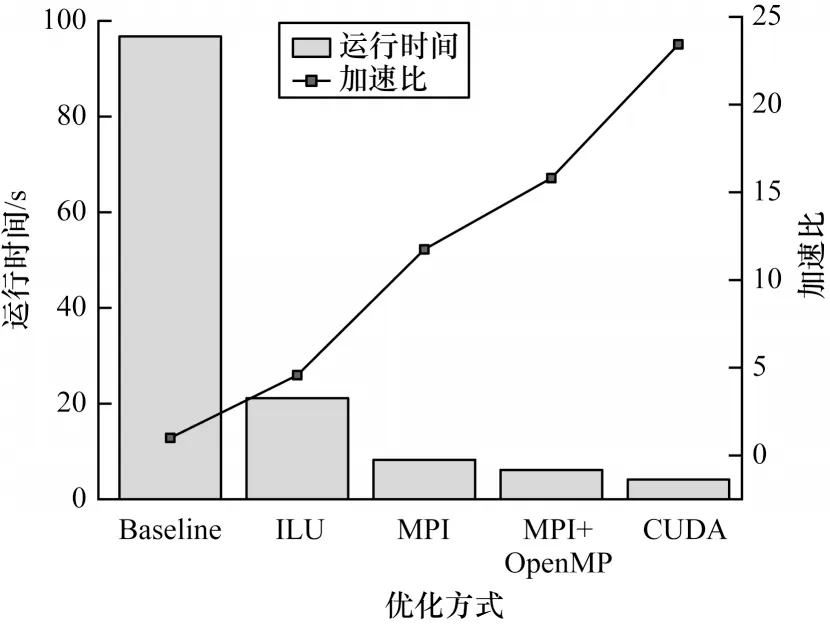
圖11 不同并行方式的優(yōu)化性能對比Fig.11 Optimization performance comparison of different parallel methods

4 結(jié)束語

大規(guī)模線性方程組的求解作為科學計算中的核心問題，長期以來都是研究者關(guān)注的重點，如何充分利用目前的高性能計算機資源對求解問題的計算性能進行優(yōu)化是重要的研究方向。本文從GRAPES 數(shù)值天氣預(yù)報系統(tǒng)動力框架中的赫姆霍茲方程求解問題出發(fā)，使用不同并行方式對廣義共軛余差法進行并行及優(yōu)化，并對計算性能進行對比分析。實驗結(jié)果表明，在MPI 并行、MPI+OpenMP 混合并行及CUDA 并行3 種優(yōu)化方式中，基于GPU 的CUDA 并行方式能夠獲得更好的計算性能。后續(xù)將建立多機混合并行的優(yōu)化模型，測試MPI+CUDA 的多節(jié)點優(yōu)化性能，同時還將分析多重網(wǎng)格預(yù)處理、稀疏近似逆預(yù)處理等其他預(yù)處理方式對迭代法收斂速度的影響。