基于DFT 尋徑的壓縮感知信道估計改進算法

方海濤，李明齊，卞 鑫

（1.中國科學院上海高等研究院，上海 201210；2.中國科學院大學，北京 100049）

0 概述

隨著5G 移動通信、毫米波、MIMO 技術的發展，人們對于信號高效率傳輸的需求日益增加，且無線移動通信的應用場景越來越復雜，因此，如何在信號準確傳輸的同時更加高效地利用有限的頻譜資源成為近年來的研究熱點。正交頻分復用（Orthogonal Frequency Division Multiplexing，OFDM）因為其頻譜利用率高、抗頻率選擇性衰落能力強等優點，成為當前以及未來移動通信的關鍵技術之一。在OFDM系統中，信號的傳輸過程受到無線信道環境衰落和延時等影響，導致產生符號間干擾（Inter Symbol Interference，ISI）。為了有效降低ISI 并提高信號傳輸的準確率，需要對信道狀態信息（Channel State Information，CSI）進行估計。

學者們對OFDM 系統的信道估計進行了大量研究。傳統的信道估計方法主要基于導頻序列進行估計，過程中需要利用大量導頻，導致系統的頻譜利用率較低［1］。壓縮感知（Compressed Sensing，CS）理論［2］通過信號的稀疏特性，可以利用較少的觀測特征來有效地恢復出初始信號。同時，由于無線信道具有稀疏性［3］，將其與壓縮感知理論相結合，可以在導頻信息較少的條件下提高頻譜利用率。

信號重構是壓縮感知理論的重要部分，其能夠將信號的低維特征恢復到高維［4-5］。文獻［6］提出的凸優化重構算法將信號重構問題轉化為優化問題，所需采樣值較少，但是存在復雜度高、難以在實際中進行應用的問題。文獻［7］提出的組合重構算法將信號采樣進行快速重構，但是其存在實際系統受限和重構精確度低的問題。在實際應用中，貪婪迭代類算法得到廣泛應用，該類算法相較于文獻［6-7］算法計算復雜度較低，且結構簡單，易于實現。根據不同的信號稀疏度條件，貪婪迭代類算法可分為基于信號稀疏度預知情況和基于信號稀疏度未知情況兩種：基于預知信號稀疏度的重構算法較為常見，如正交匹配追蹤（Orthogonal Matching Pursuit，OMP）算法［8］、壓縮采樣匹配追蹤（Compressive Sampling Matching Pursuit，CoSaMP）算 法［9］、子空間追蹤（Subspace Pursuit，SP）算法［10］等；基于未知信號稀疏度的重構算法的典型代表是稀疏度自適應匹配追蹤（Sparsity Adaptive Matching Pursuit，SAMP）算法［11］。

目前，已有很多研究人員［12-14］對基于上述算法的信道估計應用進行了分析。文獻［15］通過分級方式逐步增加重構原子的個數，并通過回歸追蹤對原子進行篩選，但其仍需要信道的稀疏度先驗信息，且對于分級步長要求較高。文獻［16-17］提出利用冪函數控制SAMP 算法迭代步長的自適應稀疏信道估計方法WSStAMP，但該方法在低信噪比時受噪聲影響較大，估計精度較低。

上述算法在信道估計中存在尋徑估計過度或估計錯誤的問題。同時，考慮到實際通信模型主要基于均勻導頻（如3GPP、5G 廣播等），現有壓縮感知信道估計研究主要是基于非均勻導頻，因此，對壓縮感知信道估計進行改進，使其適用于基于均勻導頻的實際通信環境具有重要意義。本文提出一種基于離散傅里葉變換（Discrete Fourier Transform，DFT）尋徑的OMP 信道估計方法。利用DFT 尋徑來抑制由噪聲導致的不理想原子，以對OMP 算法重構過程中的原子進行篩選，解決傳統重構算法在信道估計中存在的選徑多估和錯估問題。在此基礎上，引入一種殘差變化控制方法對信道稀疏度進行自適應估計。

1 系統模型

1.1 壓縮感知

根據CS 理論可知，若信號本身具有稀疏性或在某個變換基下具有稀疏性，以少量的觀測值就能有效恢復原始信號［1］。

設信號x是N維的離散時間信號，該信號通過一個N×N變換基矩陣和一個稀疏向量相乘獲得，則信號x可表示為：

其中：s為加權系數向量；ΨN×N為變換基矩陣。若向量s中非0 元素個數為K，且滿足K?N，則稱信號x在Ψ域內是稀疏的，稀疏度為K。

為了實現信號降維，即將N維信號減少到M維（M小于N），需要一個M×N的測量矩陣對原信號進行降維操作，從而獲得包含信號x大部分信息的測量向量y：

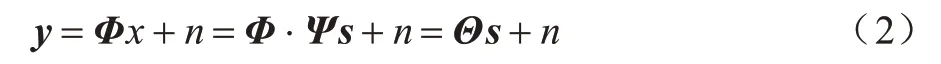
其中：Φ為M×N維的測量矩陣。因為信號x在Ψ域內是稀疏的，所以測量矩陣Φ和變換基矩陣Ψ相乘可以得到M×N維矩陣Θ，其稱為恢復矩陣。因為需要根據已知的測量值和恢復矩陣信息恢復原信號，所以恢復矩陣需要滿足等距約束性（Restricted Isometry Property，RIP），如下：

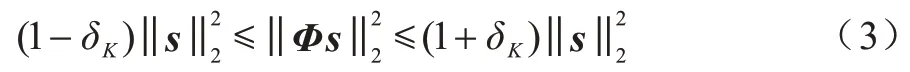
矩陣Φ滿足K 階RIP 特性，即可從s中恢復原信號。其中表示L2 范數。為對式（1）進行求解，研究人員提出了多種信號重構算法［18-20］。

1.2 OFDM 稀疏信道模型

假設OFDM 系統的子載波數目為N。在發送端，輸入的比特流經過編碼、調制、子載波映射、導頻插入等操作后得到頻域發送信號X(k)，k=0，1，…，N-1。令導頻個數為P，信道長度為L，則接收信號可表示為：

其中：X表示主對角線為X(k)（k=0，1，…，N-1）的對角矩陣；y=[y(0)，y(1)，···，y(N-1)]T為接收信號；H=[H(0)，H(1)，···，H(N-1)]T為信道頻域響應采樣；n為復加性高斯白噪聲；W為N×N維傅里葉變換矩陣的前L列。W表示如下：

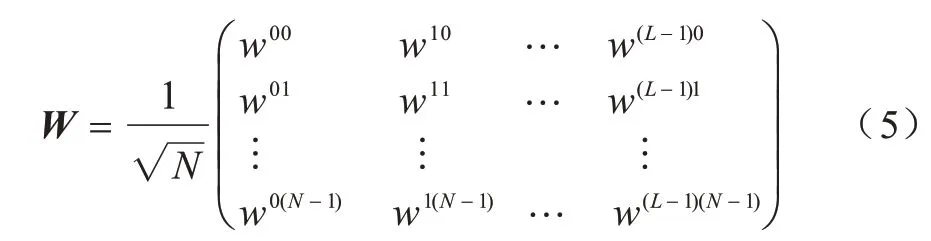
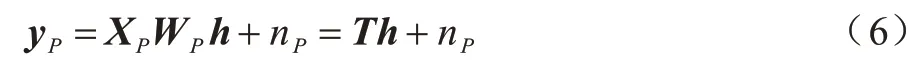
其中：XP為從N個子載波位置中選擇出的P個導頻位置，令S為N維單位矩陣中選擇出的與導頻位置對應的P行，則XP=SXST，WP=SW。從yP、XP、WP中估計h為稀疏信號重構問題，同時，在小間隔均勻導頻條件下恢復矩陣滿足等距約束性，不同導頻間隔下測量矩陣的相關性如圖1 所示。

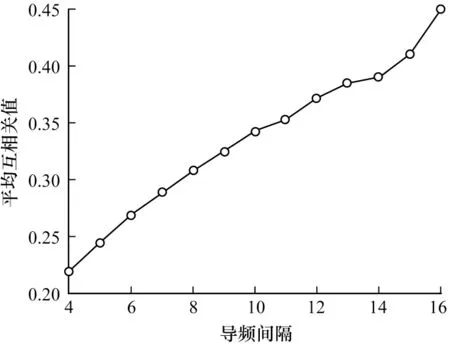
圖1 不同導頻間隔下測量矩陣的相關性Fig.1 Correlation of measurement matrix under different pilot intervals

2 基于DFT 尋徑的壓縮感知信道估計

2.1 傳統DFT 信道估計算法

傳統的DFT 信道估計算法主要是基于LS 信道估計、時頻域變換、降噪處理等信號處理過程來提高信道估計的性能。傳統的DFT 信道估計算法步驟如下：

步驟1通過LS 估計得到導頻位置的CFR：

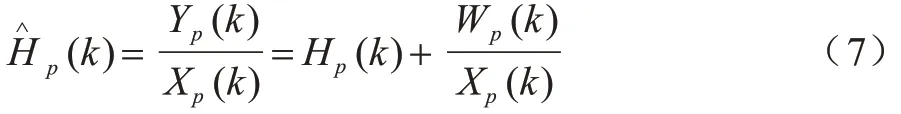
其中：Yp(k)表示第p個子載波上的接收導頻信號；Xp(k)表示第p個子載波上的發送導頻信號；Wp(k)表示第p個子載波上的頻域噪聲信號。

步驟2對LS 估計得到的導頻CFR 進行N 點IDFT 變換到時域，得到時域CIR：

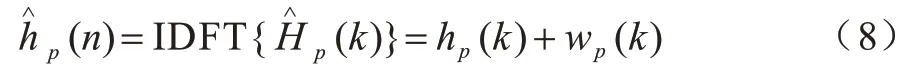
由于CIR 的長度小于CP 的長度，因此對CIR 僅保留前循環前綴長度的采樣點，將其余部分視為噪聲并置零，最后將其補零至N 點，即：

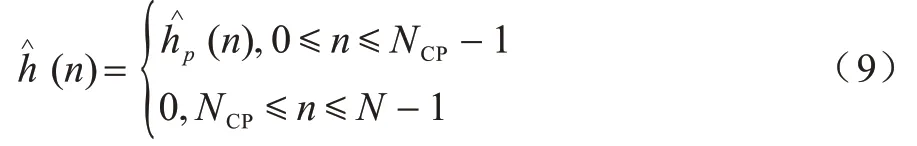
其中：NCP表示CP 的長度；N表示子載波總數。

步驟3利用時域補零等效于頻域內插信號處理的原理，獲得全部N個子載波的CFR：

2.2 基于閾值降噪的DFT 信道尋徑算法

傳統的信道估計算法將循環前綴長度以外的噪聲置零，從而消除噪聲。但是，由于循環前綴內仍然含有噪聲，因此基于DFT 的信道估計算法的性能仍有待提升。本文提出一種基于閾值降噪的DFT信道尋徑算法，以處理循環前綴內的噪聲。算法流程如圖2 所示。

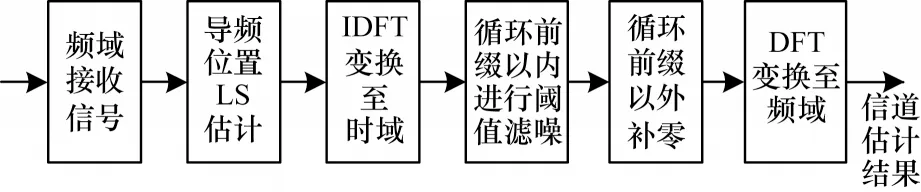
圖2 基于閾值降噪的DFT 尋徑算法流程Fig.2 Procedure of DFT path searching algorithm based on threshold noise reduction

基于閾值降噪的DFT 信道尋徑算法步驟為：首先，對LS 估計得到的信道頻域響應通過傅里葉反變換為時域響應；然后，提取循環前綴以外的樣本能量均值以及循環前綴以內的樣本能量均值，通過自定義加權系數來獲得最終的閾值；最后，對于循環前綴以內的樣本，將大于閾值的樣本保留，小于閾值的樣本置零，同時令循環前綴以外的樣本置零。

DFT 信道尋徑算法閾值的計算方法如下：

1）對循環前綴以外的噪聲求均值：

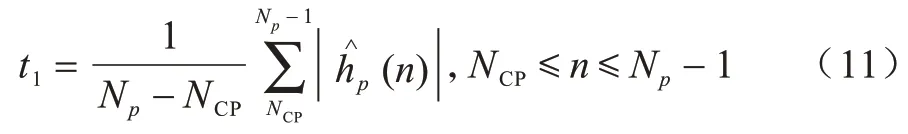
2）求得循環前綴以內的樣本能量的均值：

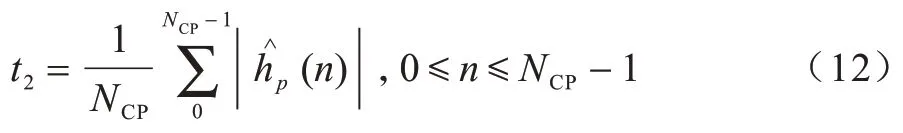
3）通過加權系數a來確定閾值的取值：

對由LS 估計得到的CIR，有：

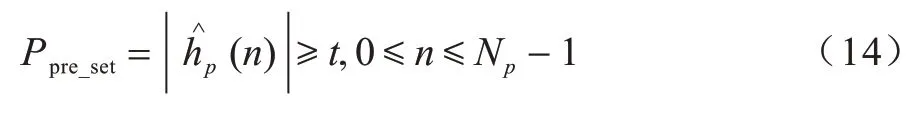
2.3 基于DFT 尋徑的OMP 信道估計

基于DFT 尋徑的OMP（DFT-OMP）信道估計算法的原理為：將基于閾值降噪的DFT 信道尋徑算法作為先驗，對傳統OMP 重構算法的處理流程進行優化，將信道沖擊響應中的非零徑區域作為OMP 重構算法中的原子預選并進行優化，從而提高重構性能。算法流程如圖3 所示，其中，虛線箭頭為沒有交集情況下的流程。

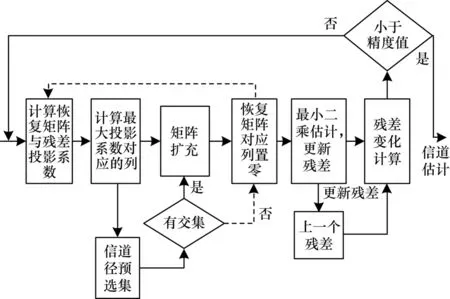
圖3 DFT-OMP 算法流程Fig.3 Procedure of DFT-OMP algorithm

DFT-OMP 信道估計算法步驟如下：

輸入信號y，恢復矩陣T，迭代次數m，信道徑預選集P

輸出信號估計值

初始化殘差矢量rn=y，增量矩陣A，時延矢量τtap，估計信道h∧，迭代變量t

步驟1更新迭代變量t=t+1，計算恢復矩陣的列向量和殘差的投影系數內積值，p=|THrn|。

步驟2在信道徑預選集合P中選擇最大投影位置Ppos=max{p}，并將對應位置的恢復矩陣列放入增量矩陣中，A=[A T(：，Ppos)]，并對恢復矩陣已投影矢量置零。

步驟3最小二乘估計。

步驟4更新殘差矢量，更新延遲矢量τtap=[τtapPpos]。

步驟5若迭代變量t小于預設迭代次數，或者殘差變化大于設定精度ε，則返回步驟2；否則，退出迭代。

殘差變化精度ε的計算公式如下：

其中：rn-1和rn分別表示上一次的殘差與更新殘差。為了更好地控制殘差變化精度，ε的取值范圍為0.01≤ε≤0.1。

傳統OMP 算法在原子預選階段選取內積最大的原子作為重構原子，如果在預選過程中出現錯誤原子，則會降低算法的重構精度，影響重構效率。為了提高重構精度，本文所提算法在原子預選后，通過引入由基于閾值降噪的DFT 信道尋徑得到的信道預選先驗集來控制原子選擇范圍，可保證在一定先驗條件下，所選擇原子與重構原子具有較大的相關性，即預選原子更適用于重構。同時，通過比較上一個殘差和當前殘差的幅值變化程度來控制重構估計的信道路徑個數，從而提高信道估計的精度。

3 仿真結果與分析

本文利用MATLAB 軟件對算法進行仿真及性能評估，實驗參數設置如表1 所示。

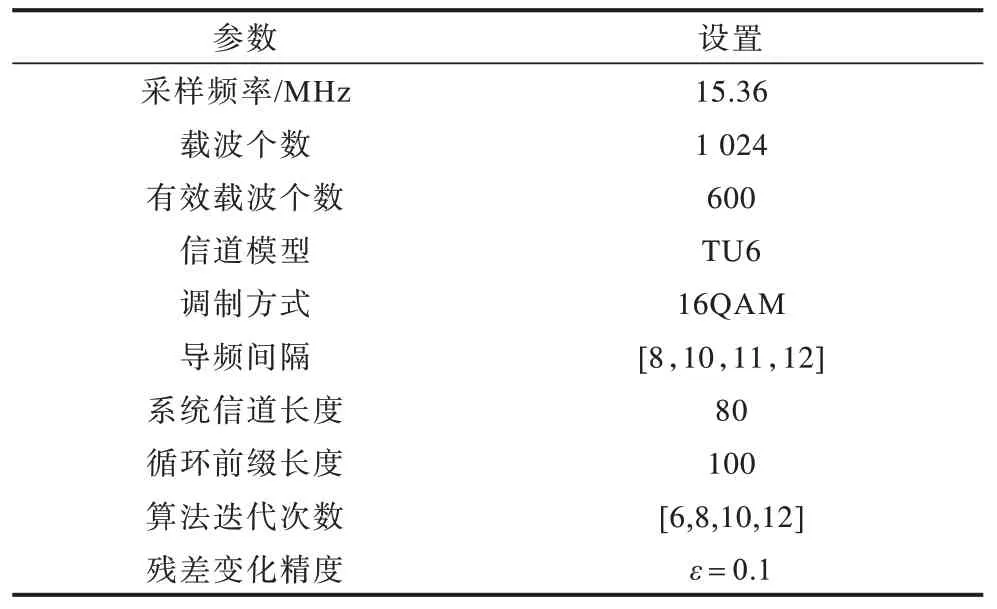
表1 實驗參數設置Table 1 Experimental parameters setting

本文利用均方誤差（Mean Square Error，MSE）驗證DFT-OMP算法的信道估計效果。均方誤差定義如下：

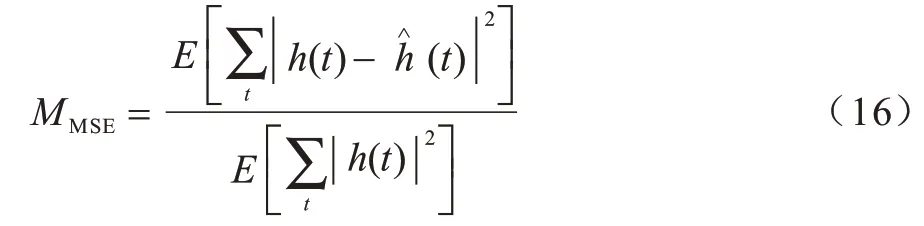
3.1 均方誤差性能比較

在導頻間隔為10 時，DFT 算 法、OMP 算 法、SAMP 算法、WSStAMP［18］算法、本文DFT-OMP 算法的信道估計均方誤差結果如圖4 所示，為保持一致性，OMP 算法和DFT-OMP 算法的迭代次數均為8。從圖4 可以看出：在相同信噪比條件下，DFT-OMP 算法的MSE 性能均優于對比算法；WSStAMP 算法在SAMP 算法的基礎上調整迭代時步長的收斂，具有更好的估計性能，但是WSStAMP 算法在低信噪比下易受噪聲影響，DFT-OMP 算法相較于WSStAMP算法約有0.5 dB 的性能增益。

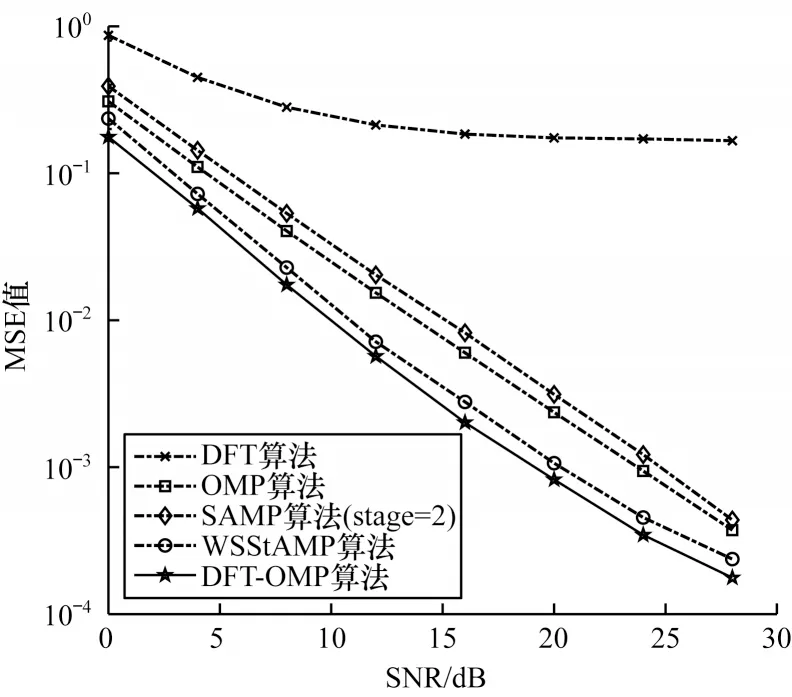
圖4 不同算法的MSE 性能比較Fig.4 Comparison of MSE performance of different algorithms

3.2 導頻個數對算法性能的影響

圖5 所示為DFT-OMP 算法與傳統OMP 算法的均方誤差性能對比。從圖5 可以看出：在相同導頻條件下，DFT-OMP 算法的MSE 性能明顯優于OMP算法；在不同導頻間隔下，隨著導頻間隔P的增大，算法的估計性能逐漸降低，當導頻間隔為12 時，DFT-OMP 算法在低信噪比時有更好的估計性能，相對OMP 約有4 dB 的性能增益，高信噪比時MSE 變化平緩，總體上仍優于OMP 算法，這是由于DFTOMP 算法通過DFT 尋徑對原子進行預選，在重構時減少噪聲對重構原子選取的影響，同時利用殘差變化對OMP 算法的迭代次數進行控制，保證算法迭代具有自適應性和魯棒性。

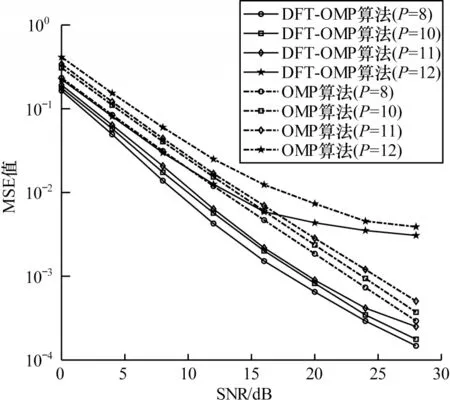
圖5 不同導頻間隔下的MSE 性能比較Fig.5 Comparison of MSE performance under different pilot intervals

3.3 迭代次數對算法性能的影響

在實際應用中，過多的迭代會帶來信道估計的冗余，從而影響信道估計性能。圖6 所示為DFTOMP 算法與OMP 算法在不同迭代次數下的性能對比。從圖6 可以看出：OMP 算法依賴于信號稀疏度的先驗信息，隨著迭代次數的增加，算法估計性能降低；隨著迭代次數的增加，DFT-OMP 算法的估計性能明顯優于OMP 算法，原因是DFT-OMP 信道估計算法引入殘差變化控制，避免引入無關重構原子，保證在較大的迭代次數下也能較好地進行信道估計；DFT-OMP 算法在較高信噪比時逼近理想徑（已知徑位置）下的信道估計性能。

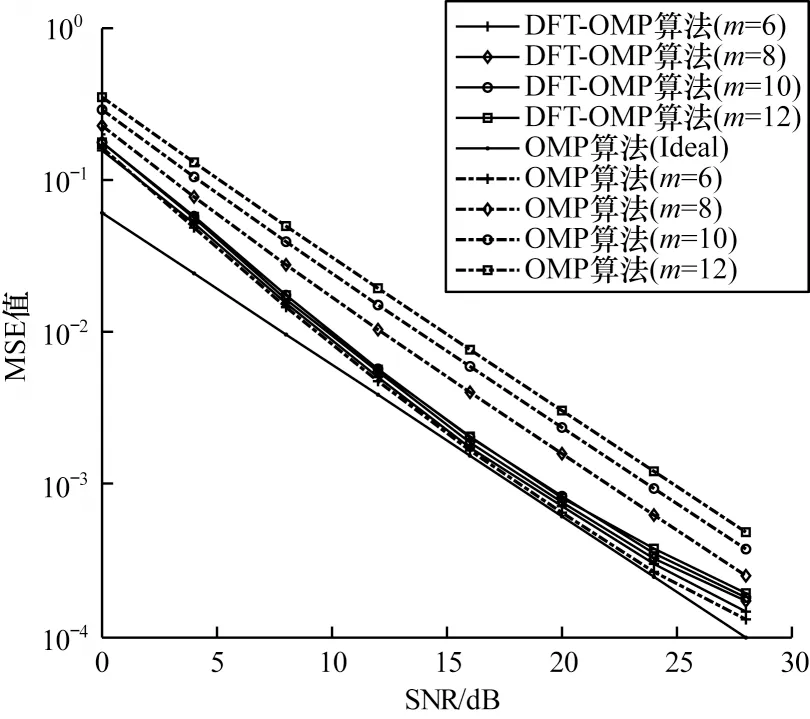
圖6 不同迭代次數下的MSE 性能比較Fig.6 Comparison of MSE performance under different iterations

3.4 閾值對算法性能的影響

在SNR 為28 dB 時，不同閾值下DFT-OMP 算法的MSE 性能如圖7 所示。從圖7 可以看出：閾值選取對算法性能有一定影響，且在不同導頻間隔下，性能變化基本保持一致；當閾值選取較大時，去除的原子中可能存在重構所需的原子，從而導致估計性能下降；當閾值較小時（α<0.2），噪聲原子可能影響重構原子的選取，從而影響估計性能；當閾值設置為0.2 時算法能取得較好的估計性能。

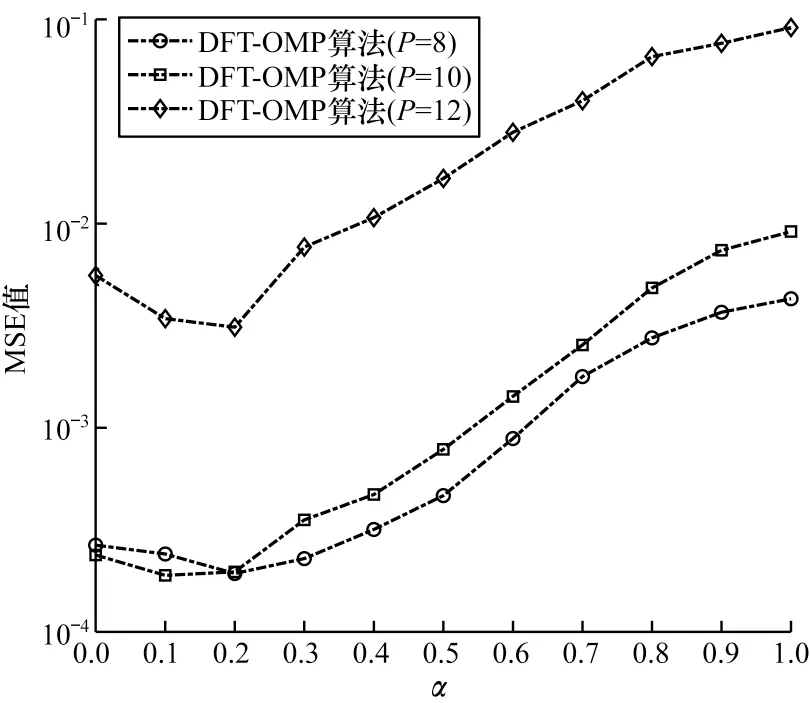
圖7 不同閾值下的MSE 性能比較Fig.7 Comparison of MSE performance under different thresholds

表2 所示為4 種算法在不同導頻間隔下的運算時間比較，仿真硬件參數為Intel i7-4710HQ，CPU 為2.50 GHz，RAM 為4.00 GB，Microsoft Windows 10 操作系統。從表2 可以看出：DFT-OMP 算法在計算復雜度上較OMP 算法有少量提升；SAMP 算法相較于OMP 算法復雜度明顯提高；WSStAMP 算法通過冪函數來選取步長，降低了SAMP 算法的復雜度，但仍高于DFT-OMP 算法。結合圖4～圖6 以及表2 可以看出，DFT-OMP 算法在犧牲少量運算時間的條件下可以有效提高信道估計性能。

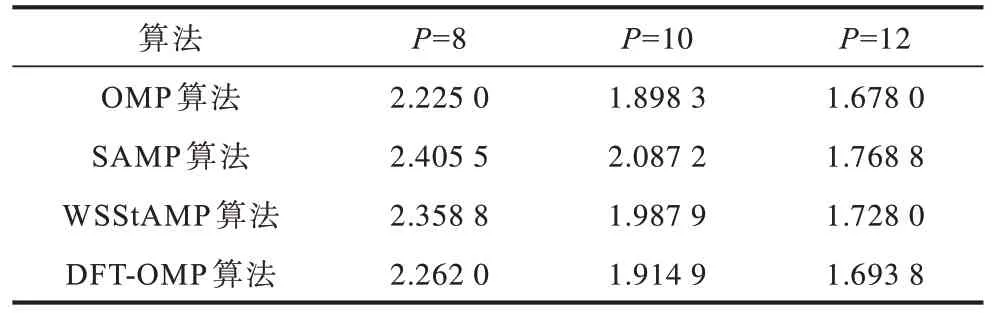
表2 4 種算法在不同導頻間隔下的運算時間比較Table 2 Comparison of operation time of four algorithms under different pilot intervals s

4 結束語

針對傳統均勻導頻條件下壓縮感知信道估計精度較低的問題，本文提出一種在均勻導頻下基于DFT 尋徑的OMP 信道估計算法。在傳統OMP 算法的基礎上設計一種尋徑先驗方法，以對算法中的原子進行預選，通過基于閾值DFT 尋徑的方式來抑制由噪聲導致的不理想原子，從而實現原子優化。同時，引入控制殘差變化精度的方法約束算法迭代，在提高信道估計性能的同時提升算法的自適應性與魯棒性。仿真結果表明，相較OMP 算法，該算法在較大均勻導頻的條件下具有更好的估計性能和更低的算法復雜度。后續將運用該算法解決實際通信系統中由虛擬子載波引起的頻譜泄露問題，進一步提升算法的估計性能。