滲透模型思想 提升數(shù)學(xué)素養(yǎng)
——以“將軍飲馬問題及其拓展”專題復(fù)習(xí)課為例

■顏小兵

一、設(shè)計背景

中考數(shù)學(xué)復(fù)習(xí)課是初中生進(jìn)行系統(tǒng)學(xué)習(xí)的最后一環(huán)。作為一線教師，我們要努力讓學(xué)生將知識結(jié)構(gòu)進(jìn)行優(yōu)化，提高學(xué)生的思維水平和認(rèn)知能力。本節(jié)課選取的課例是中考數(shù)學(xué)專題復(fù)習(xí)課“將軍飲馬問題及其拓展”。該問題模型建構(gòu)、思考過程簡單巧妙，與其他相關(guān)知識結(jié)合后有許多妙用，貫穿初中數(shù)學(xué)始終，是一節(jié)具有很強(qiáng)代表性的復(fù)習(xí)課。

二、教學(xué)目標(biāo)

讓學(xué)生了解“將軍飲馬”問題模型并理解模型的本質(zhì)；挖掘幾何圖形中的隱含條件，歸納總結(jié)“兩定一動”類型的題目特點并轉(zhuǎn)化；培養(yǎng)學(xué)生建模和轉(zhuǎn)化問題的能力，發(fā)展學(xué)生的空間想象能力和邏輯推理能力。

三、教學(xué)過程

1.引入情境，解析模型。

問題1：古希臘一位將軍要從A地出發(fā)到河邊MN處飲馬，然后再回到駐地B。問該將軍怎樣選擇飲馬地點，才能使路程最短？

可在河邊飲馬的地點有許多處，現(xiàn)在的問題是怎樣找出使兩條線段長度之和最短的那個點。教師要引導(dǎo)學(xué)生做輔助線（如圖1）。

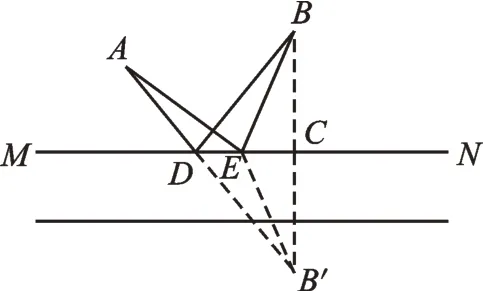
圖1

2.觀察探究，合作交流。

問題2：如圖2，在等邊△ABC中，AB=6，AD⊥BC，E是AC上的一點，M是AD上的一點，若AE=2，求EM+EC的最小值。

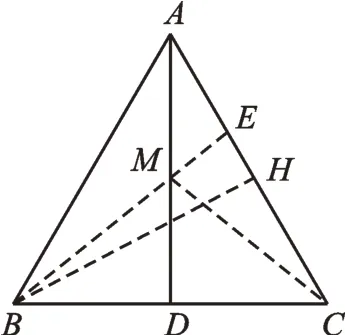
圖2

本題是“將軍飲馬”問題模型在等邊三角形中的特殊運用。等邊三角形是軸對稱圖形，底邊上的高與底邊上的中線互相重合。任意一條邊上的高都是這條邊的垂直平分線，都是等邊三角形的對稱軸。這里要提醒學(xué)生借助圖形的對稱性，根據(jù)“兩點之間線段最短”找到動點位置，再結(jié)合勾股定理求出最小值。

師：剛才同學(xué)們是利用“等邊三角形是軸對稱圖形”這一特征，直接找出對稱點，將最值問題轉(zhuǎn)化成我們熟悉的問題。下面請看問題3，在正方形中是否也能夠借助模型求最值呢？

問題3：如圖3，在正方形ABCD中，點E在BC邊上，BE=2，CE=1，點P在BD上，求PE+PC的最小值。

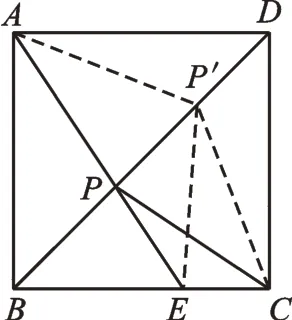
圖3

本題是“將軍飲馬”問題模型在正方形中的特殊運用。這里仍然要提醒學(xué)生，借助特殊圖形的對稱性進(jìn)行證明。

師：同學(xué)們，圓是軸對稱圖形，它的對稱軸是直徑所在的直線。在問題4 中，求兩條線段之和的最小值，能否根據(jù)圓的對稱性，聯(lián)想到“將軍飲馬”問題模型去解決呢？

問題4：如圖4，AB是⊙O的直徑，AB=4，點C是半圓的三等分點，點D是弧BC的中點，AB上有一動點P，連接PC、PD，則PC+PD的最小值是多少？并畫出點P的位置。

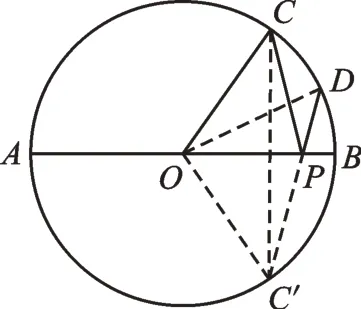
圖4

本題是“將軍飲馬”問題模型在圓中的特殊運用。教師要提醒學(xué)生緊緊抓住圓既是中心對稱圖形，又是軸對稱圖形的特征。只要抓住模型的本質(zhì)特征，借助對稱性，根據(jù)“兩點之間線段最短”，找到動點的位置并不困難。

3.變式提升，拓展創(chuàng)新。

師：同學(xué)們，以上3 個問題都是借助“將軍飲馬”問題模型，根據(jù)等邊三角形、正方形、圓的軸對稱性求解的。下面我們來看一下，在二次函數(shù)以及平面直角坐標(biāo)系中，如何聯(lián)想到“將軍飲馬”問題模型求線段和的最小值。

問題5：如圖5，拋物線y=ax2+c經(jīng)過A（0，1），P（2 3，-3）。（1）求表達(dá)式并判定C（ 3，0）是否在此拋物線上；（2）若M是拋物線對稱軸上的動點，連接MP、MC，試求△PCM周長的最小值。

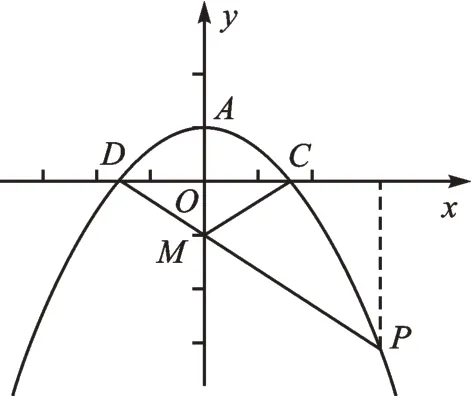
圖5

問題6：如圖6，在平面直角坐標(biāo)系中，長為2的線段CD（點D在點C的右側(cè)）在x軸上移動，A（0，2），B（0，4），連接AC、BD，求AC+BD的最小值。

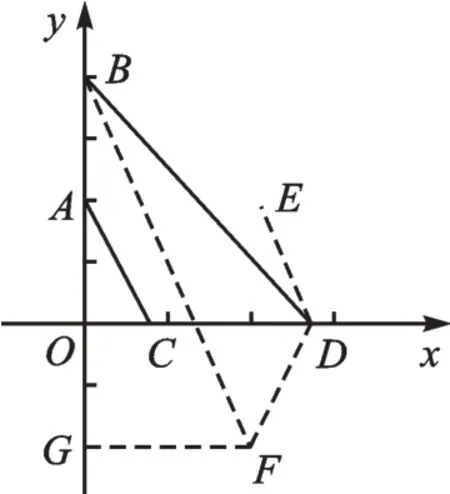
圖6

4.聯(lián)系實際，綜合運用。

師：數(shù)學(xué)來源于生活，生活中的許多實踐活動都與數(shù)學(xué)有關(guān)。譬如，在一個圓柱體上，如何求小蟲爬行的最短路徑呢？

問題7：如圖7，桌上有一圓柱形玻璃杯，高12cm，底面周長18cm，在杯內(nèi)壁離杯口3cm 的A處有一滴蜜糖，一條小蟲從桌上爬至杯子外壁，當(dāng)它正好爬至蜜糖相對方向離桌面3cm 的B處時（即A、B在底面的射影的連線經(jīng)過底面的圓心O），突然發(fā)現(xiàn)了蜜糖。小蟲怎樣爬，到蜜糖的路程最短？

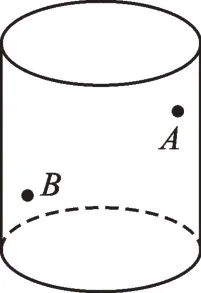
圖7

這是一道將“將軍飲馬”模型應(yīng)用到實際生活的典型問題。在講解過程中，教師可以將立體圖形展開成平面圖形，引導(dǎo)學(xué)生看清題目的本質(zhì)，利用建模思想解決問題。

四、教學(xué)反思

典型的“將軍飲馬”問題屬于“一動兩定”型問題，其本質(zhì)就是將同側(cè)兩折線段之和，通過軸對稱轉(zhuǎn)化為異側(cè)兩折線段之和。它與三角形、四邊形、圓、函數(shù)及實際生活緊密聯(lián)系在一起，雖然每個題目的呈現(xiàn)形式不同，但解決問題的本質(zhì)方法不變，往往需要通過作輔助線，將問題轉(zhuǎn)化為“將軍飲馬”問題，最后利用“兩點之間線段最短”的基本事實解決。本節(jié)課研究的重點實際上是圖形之間的位置關(guān)系，以及由一個圖形得到另一個圖形的軸對稱變換。只要引導(dǎo)學(xué)生掌握模型本質(zhì)，挖掘知識點之間的聯(lián)系，許多問題便可以迎刃而解。在教學(xué)過程中，教師要積極滲透數(shù)學(xué)模型思想，講清、講透每個數(shù)學(xué)模型，讓學(xué)生能看清知識的本質(zhì)，觸類旁通，這樣才能幫助學(xué)生拓寬數(shù)學(xué)知識面，促進(jìn)學(xué)生分析問題和解決問題能力的提高，進(jìn)一步發(fā)展學(xué)生的數(shù)學(xué)核心素養(yǎng)