教師要腳踏實地，也要仰望星空
——從一道基本功大賽筆試題談教師的專業素養提升

■常靜鋒

筆者最近參加了靖江市初中數學青年教師教學基本功大賽。在筆試環節，有這樣一道幾何證明題：請用直接證明的方法求證對角互補的四邊形是圓的內接四邊形。即：

已知：如圖1，在四邊形ABCD中，∠A+∠C=180°，求證：四邊形ABCD內接于一個圓。

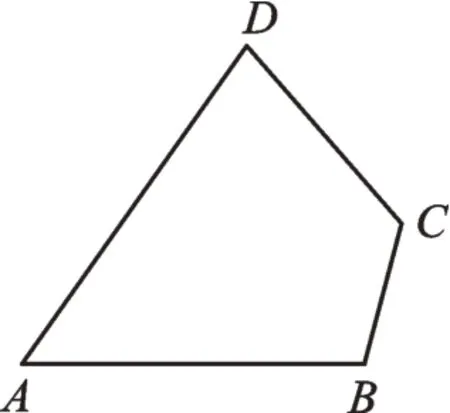
圖1

筆者由于經常參加所在市初中數學試卷的調研、命題，所以，對于初中數學解題，還是比較自信的。看到這樣的問題，筆者首先想到了反證法。

如圖2，過A、B、C三點作⊙O，假設點D不在⊙O上，則點D可能在⊙O內或在⊙O外。

圖2

假設點D在⊙O內，連接并延長BD必與⊙O相交。設交點為D′，連接AD′、BD′，則必有∠AD′C+ ∠ABC=180°，因為∠AD′B＜∠ADB，∠CD′B＜∠CDB，所以∠AD′C＜∠ADC，所以∠ADC+∠ABC＞180°，這與“∠A+∠C=180°”矛盾，說明點D不可能在⊙O內。同樣可證明點D不可能在⊙O外，故點D只能在⊙O上，即四邊形ABCD內接于一個圓。

我們知道，一個命題的逆否命題與原命題等價，而反證法的本質就是證明原命題的逆否命題。通常在直接證明比較困難的情況下，用反證法更容易。這道題也可用直接證明的方法，但是，參加比賽的教師中居然沒有一位教師能夠直接證明出來。考試結束后，數學教研員給我們進行了講解：

由于∠A+∠C=180°，而四邊形ABCD的內角和為360°，所以∠A+∠C=∠B+∠D。

（1）若∠A=∠B，則∠C=∠D，有四邊形ABCD是等腰梯形，且AB//CD（如圖3）。作AB的垂直平分線l1，l1必然垂直平分CD，作AD的垂直平分線l2，l2交直線l1于點O，連接AO、BO、CO、DO，則有AO=BO=CO=DO，所以四邊形ABCD一定有外接圓。

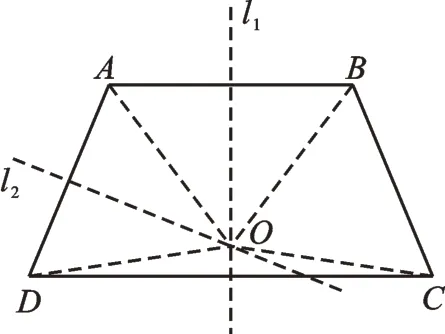
圖3

（2）若∠A≠∠B，不妨設∠A＞∠B，由∠A+∠C=∠B+∠D，有∠A-∠D=∠B-∠C。

如圖4，分別在∠A、∠B內作射線AG、BG，使得∠1=∠D、∠2=∠C，兩條射線相交于點G，且分別與CD相交于點E、點F。

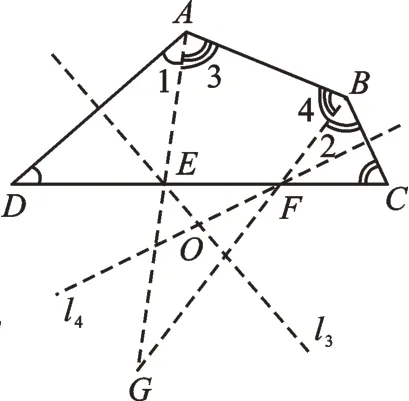
圖4

如果點G恰好在CD邊上（即E、F、G三點重合），則有GA=GB=GC=GD，那么四邊形ABCD內接于一個圓。

如果點G不在CD邊上，分別作AD、BC的垂直平分線l3、l4相交于點O，所以OA=OD，OB=OC。

因為∠1=∠D、∠2=∠C，所以EA=ED、FB=FC，故OE平分∠GEF，OF平分∠EFG，所以在△EFG中，點O必在∠G的角平分線上。

而∠A-∠D=∠B-∠C，即∠3=∠4，所以AG=BG，所以直線GO垂直平分AB，即OA=OB，所以OA=OB=OC=OD。故以O點為圓心、OA長為半徑的圓經過B、C、D三點，即四邊形ABCD內接于一個圓。

筆者驚嘆道：“原來這道題還可以這樣證明啊！”顯然，直接證明的方法仍然基于初中幾何知識。筆者在享受這道題直接證明方法的同時，也產生了一種深深的自責，不禁想起裴光亞先生在《青年教師的專業成長》中的一段話：“不論你具備什么樣的學歷，畢業于哪個院校，如果沒有進取的愿望，沒有人生意義的追求，沒有理想，沒有對教師使命的崇高理解，你的水平都將向同一個層次聚焦，這個層次便是中學。沿著阻力最小的方向，這是一個極限的過程。若以中學水平為極限，當你以高學歷為起點時,這將是一個單調下降的過程。”這段文字好像就是筆者的自畫像。

筆者反思自己的教學生涯，無非就是備課、上課、批改作業、輔導學生應試，有時還會為自己擅長解中考題，教的學生考高分而沾沾自喜。殊不知，長期下去，自己的專業水平逐漸下降，學科素養明顯削弱。通過一段時間的閱讀、實踐與反思，筆者體會到，要想成為一名優秀的初中數學教師，既要腳踏實地，也要仰望星空；既要有大知識觀、數學哲學觀，還要有素質教育觀。

數學教師要有大知識觀。例如，在平面幾何中，有許多教材中沒有出現的經典定理或結論，如托勒密定理、梅涅勞斯定理、笛沙格定理、塞瓦定理等，這些定理在教學中不要求學生了解，但作為初中數學教師，必須了然于心。只有這樣，教學時才能胸有成竹。

數學教師要有數學哲學觀。我們都有這樣的體會：學生學習了高中、大學內容后，總感覺初中教師是不是講錯了？以“平行線的定義”為例，初中教材上是這樣描述的：在同一平面內，不相交的兩條直線叫作平行線。這是基于歐氏幾何的結論。事實上，非歐幾何認為：在同一平面內任何兩條直線都有公共點（交點）。這是由“改進”的球面模型得出的基本公設。我們可以設想：教師如果有數學的高觀點，上課就不會對學生說出“過頭”的話，學生也不會認為初中教師講錯了。數學教師不能只研究教材，研究學生，研究教法，還應該多閱讀，與名家對話，與大師對話。如了解數學的起源在哪里，數學是發現的還是發明的，數學的對立與統一等。數學教師只有通過閱讀，才能感悟數學的哲學意蘊，使自己有數學哲學的高觀點。

數學教師要有素質教育觀。教育不只在于傳授知識，還應該熏陶學生的精神和情感。比如，本文中的第一個案例，因為中考試題中不會出現，所以教學中不可能涉及。但教師如果課堂上引導學生進行探究，作出完整的證明，學生自然能從中感受到數學的奇妙，從而激發幾何探究的興趣，數學的理性精神也會得到熏陶