基于北斗三號衛星非差多普勒觀測信號的優化測速模型

王澤杰，王潛心，商天文

基于北斗三號衛星非差多普勒觀測信號的優化測速模型

王澤杰1，王潛心1，商天文2

（1. 中國礦業大學環境與測繪學院，江蘇 徐州 221116 ；2. 國網物資有限公司，北京 100054）

針對運動載體速度估計方法精度不足、模型復雜等問題，提出了一種精度高、模型復雜度低的基于北斗三號衛星非差多普勒觀測信號的優化測速模型。該模型利用北斗三號衛星原始數據，使用復雜度低的多普勒測速模型估計載體速度。為提高測速精度和解算效率，首先對原始模型線性化處理，然后依據載體航向與其速度矢量的相關性增加松約束。用北斗三號衛星實測數據驗證了該模型的測速精度，評估了該模型的適用性。實驗結果表明，載體靜止時，優化多普勒測速精度可達cm/s級甚至mm/s級，在與原始多普勒測速的對比中，水平方向測速精度提高60%左右，解算時間縮短24%；載體運動時，增加航向約束的多普勒測速精度與原始多普勒測速相比，北、東方向測速精度可提高14%～21%，解算效率提升大約20%。

北斗三號衛星；多普勒；航向；松約束；線性化

1 引言

速度是載體運動狀態的重要參數，全球衛星導航系統（global navigation satellite system，GNSS）因其具有高精度、高實時性和成本低的優點，在測速領域被廣泛研究。為了提高測速精度，Greenspan等[1]提出基于GPS的L1載波的測速模型，并通過建立對流層、電離層延遲誤差改正模型，使靜態測速精度達毫米級，但當觀測環境變化時改正模型并不適用。為消除不同環境下對流層、電離層延遲誤差對速度測定的影響，可建立站間、星間雙差觀測方程[2]，但這種方法的缺點是需要兩臺相距小于10 km的GNSS接收機同步觀測，當載體行駛范圍擴大時，需要架設更多接收機。為解決人力和儀器成本增加的問題，可將單接收機的載波相位與多普勒觀測信號結合，從而有效消除周跳干擾、抑制高頻噪聲影響[3]，但衛星不足時僅增加觀測類型不能得到可靠的測速結果。通過法方程疊加融合GPS和GLONASS數據聯合測速[4]可增加衛星數量，從而增加線性無關方程。根據北斗系統（beidou navigation satellite system，BDS）與GPS系統間偏差的研究[5-6]，GPS/BDS雙系統定位定速模型可以完全融合GPS和BDS觀測數據[7]。GPS/BDS測速跳變情況則可通過廣播星歷更新法避免[8]。對比GPS、BDS和GPS/BDS組合定位和定速效果，證明GPS/BDS測速精度更高[9]。多衛星系統聯合測速仍然存在可見衛星不足的情況，慣性導航系統（inertial navigation system，INS）作為獨立的導航系統可當作載體測速的主要方法，將它與多普勒測速結合，可有效抑制單一INS的位置發散[10]。將捷聯式慣性導航系統（strap-down inertial navigation syetem，SINS）與GNSS通過卡爾曼濾波組合可實現短時間內的較高精度的組合測速[11]。通過建立復雜的模型，測速精度得到提升，但解算時間延長，考慮每5 m的定位偏差僅產生1 mm/s的定速偏差[12]，在建模時所用的載體位置可使用耗時較少的偽距單點定位方法；為更進一步簡化模型，可將測速模型線性化，效率提升近40%，但這種方法存在誤差累積，測速精度隨時間推移而降低[13]。同時，北斗三號衛星全球服務給高精度位置服務帶來契機[14]，實現可靠的速度解算是北斗三號衛星服務必須考慮的關鍵問題之一。

由上述載體速度估計方法可知，在速度測量模型復雜的條件下，測速的效率降低，因此本文將原始多普勒測速模型簡化；而在速度測量模型簡單的條件下，很多類型的誤差不能消除，所以精度較低，因此本文中的模型考慮到道路幾何變化與載體航向的關系，增加了簡單的松約束提高精度。同時，由于目前關于北斗三號衛星測速研究相對缺乏，為了豐富該方向的研究，本文模型采用最新的北斗三號衛星觀測數據進行實驗。

2 北斗三號衛星多普勒測速建模和優化

北斗三號衛星原始觀測方程為：

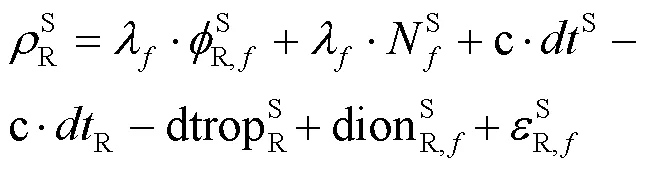
為引入多普勒觀測信息，對式（1）兩邊同時關于時間求導，即：

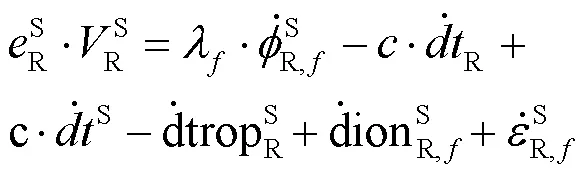
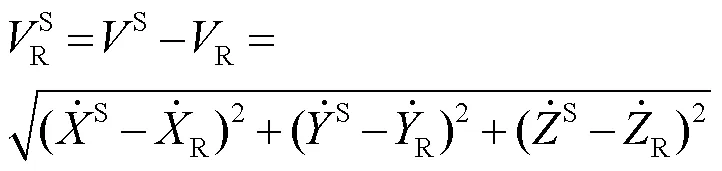
對式（2）進行簡化處理后得：

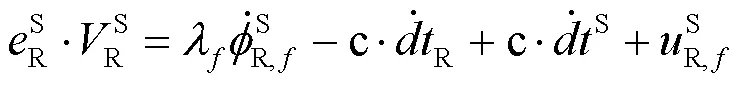
考慮到載體每個方向的參數估計，對多普勒觀測信號進行矢量分解處理，用、、表示對應的載體、與方向余弦值，即：

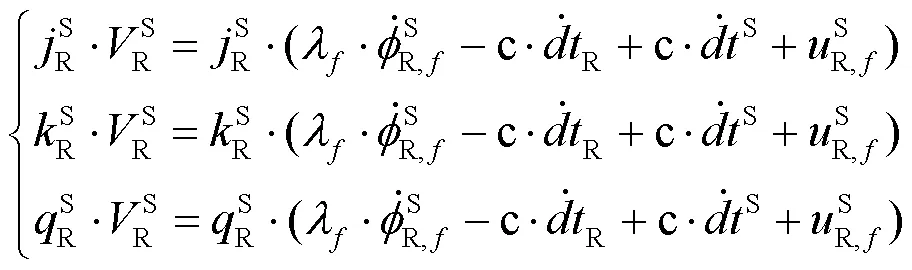
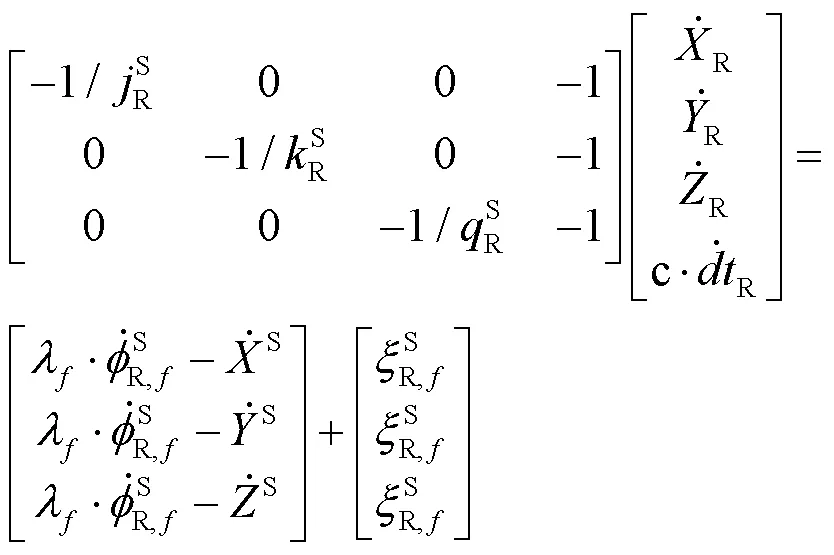
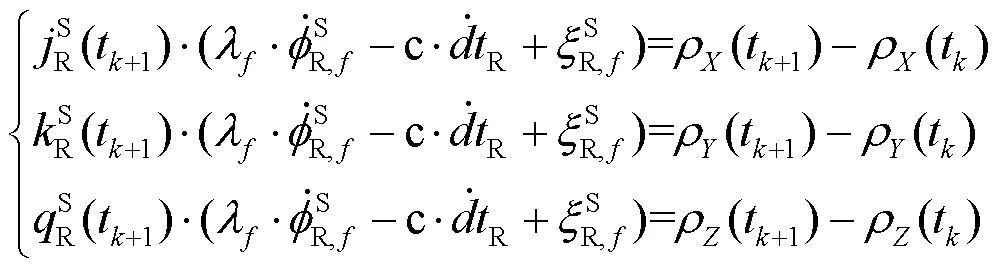
其中：

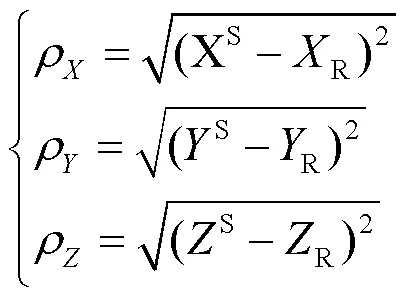
載體在t+1處的位置可以表示為：

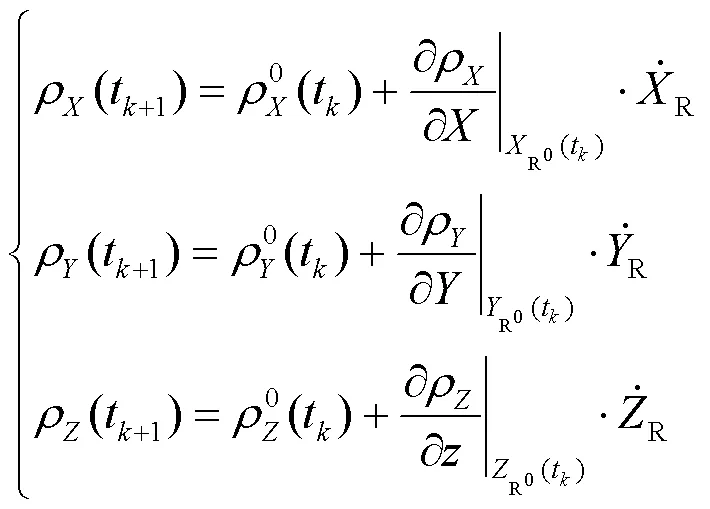
令：

聯立式（7）～式（10），可得載體不同方向的觀測方程表達式，即：

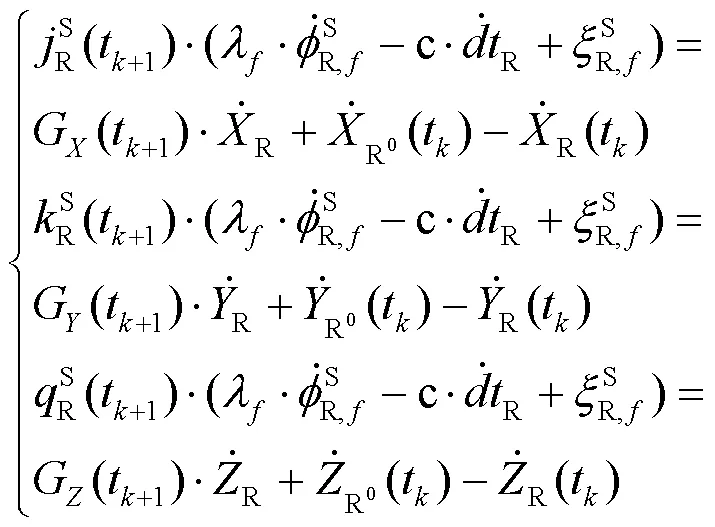
同理，另一組參數解算方程可表示為：

式（12）即線性化多普勒測速模型的矢量形式。

為進一步提高參數解算精度，結合載體運動過程中航向與速度之間的關系，可構建額外的非完整性約束方程。為便于計算，通常將速度矢量轉換至載體坐標系NEU（north, east, up），即建立站心直角坐標與空間直角坐標系下的速度關系式[15]：

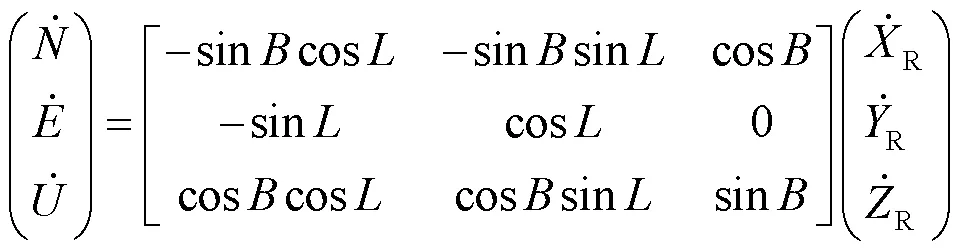
其中，和分別表示載體的大地經度、緯度。受到道路幾何形狀和載體運動限制[16]，短時間內可利用歷史軌跡曲線的割線方向代替切線方向，并作為載體的航向（以車輛為載體，如圖1所示），表示為：

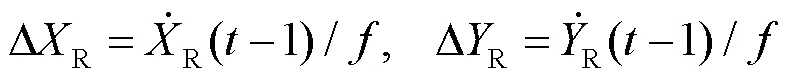
因此，考慮前一歷元的航向與當下歷元速度之間的相關性，可施加如下軟約束條件，建立附有約束信息的平差模型[17]。

其中，為載體瞬時航向角，O表示非完整性約束后的殘差。式（15）可表示為：

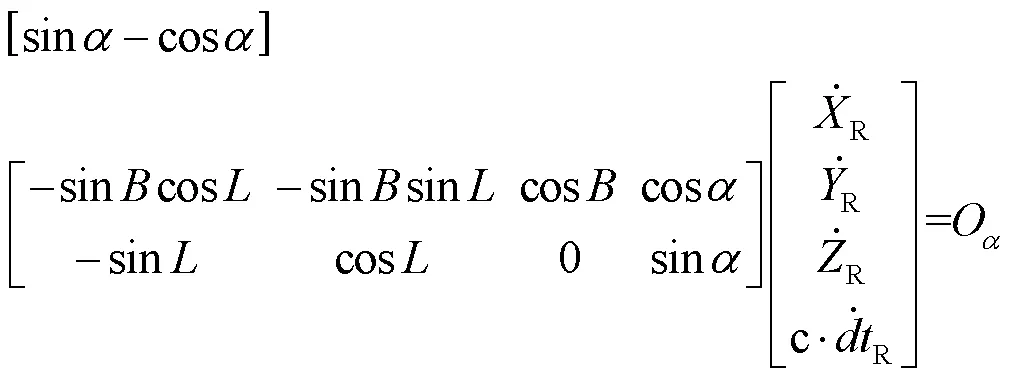
聯立式（12）和式（16）可解得載體速度。

3 實驗分析

為驗證本文提出的基于北斗三號衛星多普勒觀測信號的優化測速模型，設計了靜態和動態實驗，方案有以下3種。

方案一：利用式（6）進行載體速度解算，即原始非差多普勒測速模型。

方案二：聯立式（12）和式（16），對原始非差多普勒測速模型線性化處理后，加入航向約束進行載體速度測定，即優化非差多普勒測速模型。

方案三：使用星間、站間、歷元間差分載波相位觀測信號進行測站速度測定，即星間、站間、歷元間差分載波相位測速模型。

靜態實驗用于驗證優化模型的測速精度、解算效率以及確定動態實驗的速度參考來源。理論上，使用星間、站間、歷元間差分載波相位測速模型（方案三）可有效消除區域電離層、對流層延遲誤差，因此理論精度較高[18]，靜態實驗將驗證方案三能否作為動態實驗的速度參考值。

動態實驗用于驗證優化模型在實際的車輛行駛過程中的適用性。

3.1 靜態實驗以及動態實驗速度參考值的確定

靜態實驗于2021年2月24日在中國礦業大學進行，使用兩臺海星達iRTK5接收機同步采集北斗三號衛星數據，采樣頻率為1 Hz。由于接收機靜止，速度真值為0，所以靜態測速的解算結果即誤差。

圖1 載體行駛軌跡、切線方向和割線方向

圖2展示了第1～1 600歷元間，在站心坐標系下3種方案測速結果的誤差，灰色三角形代表原始非差多普勒測速，白色方框代表優化非差多普勒測速，黑色球形代表星間、站間、歷元間差分載波相位測速。3種方案靜態測速結果在N、E、U方向和N-E平面上誤差均值（mean）、均方根誤差（root-mean-square error，RMSE）和解算所用時間見表1。在靜態測速中，原始非差多普勒測速精度可達厘米級，優化非差多普勒測速精度可達厘米級甚至毫米級。相比原始非差多普勒測速模型，優化非差多普勒測速誤差在N、E方向上具有明顯向真值0靠攏的趨勢，其測速精度在N方向上提升了62.6%，E方向上提升了65.3%，N-E平面合速度提升了66.8%，但U方向上持平或略有降低，這是因為本文采用的航向約束本質是根據載體航向重新分配水平面上的速度分量，從而達到水平面上的合速度優化，而垂直于水平面的約束條件在本文實驗條件下可被忽略。優化非差多普勒測速解算用時比原始非差多普勒測速節省了24.3%，這是因為前者使用了復雜度較低的線性化測速模型，該模型的構造只需要已知載體初始位置，之后時刻的載體位置可通過累加位移求得，無逐歷元單點定位步驟。

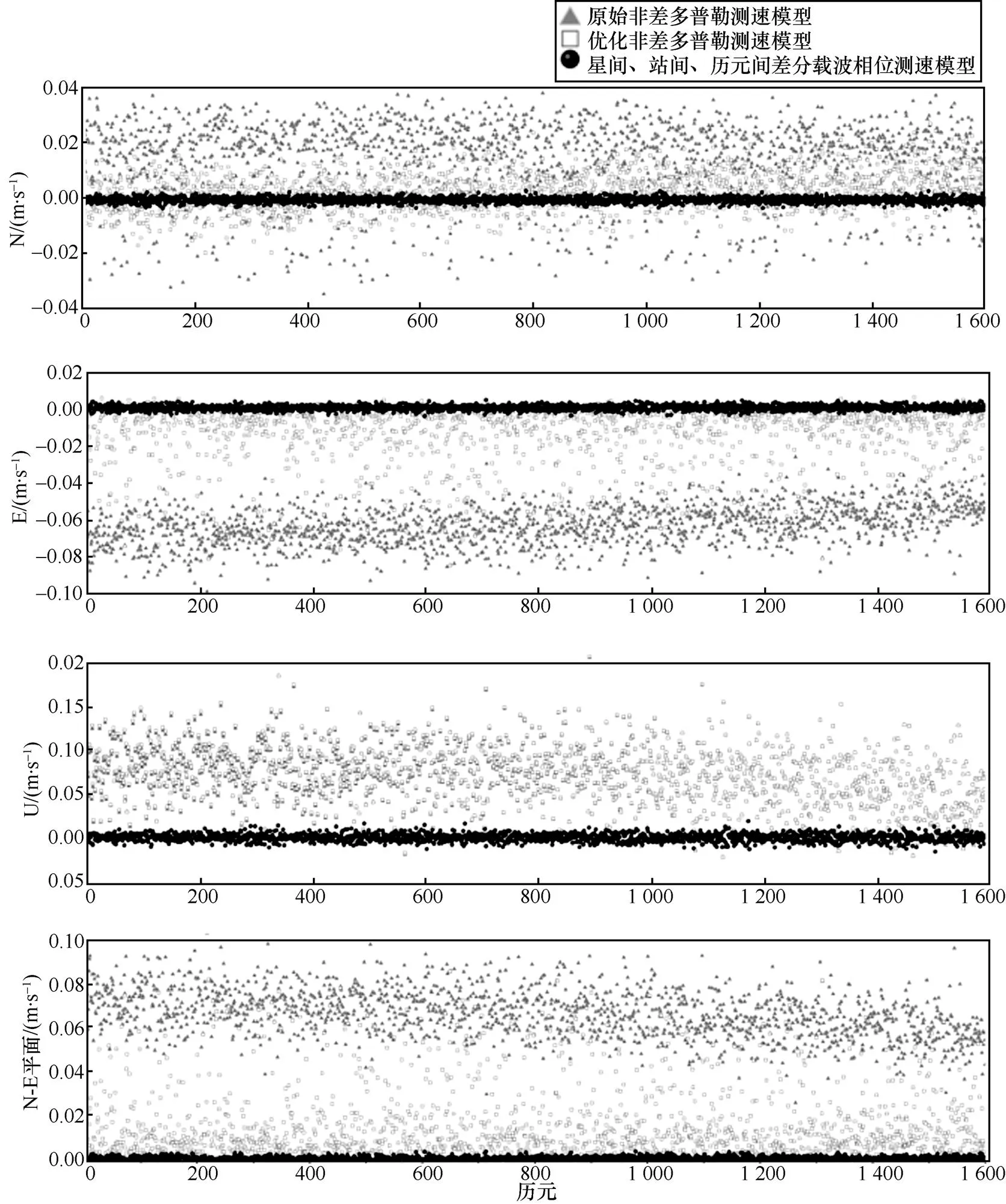
圖2 靜態實驗中第1～1600歷元的速度誤差

表1 靜態實驗中3種方案速度解的誤差對比

星間、站間、歷元間差分載波相位測速誤差可達亞毫米級，其精度遠高于使用非差多普勒觀測信號求解速度，因此可以將它作為動態實驗中的速度參考值。同時，非差多普勒測速由于只需要一臺接收機且無差分處理過程，其時效性遠高于星間、站間、歷元間差分載波相位測速。

3.2 動態實驗

動態實驗于2021年2月24日在中國礦業大學附近區域進行，車輛行駛路線及接收機架設情況如圖3所示，方案一和方案二僅使用移動接收機，參考接收機僅用于方案三中載波相位觀測信號站間差分。動態實驗中車輛近似直線運動時北斗三號衛星的星下軌跡如圖4所示，本次實驗可見北斗三號衛星包含5顆MEO衛星、1顆IGSO衛星和1顆GEO衛星，實驗區域可見北斗三號衛星的空間位置幾何精度在3～5，滿足測速模型構建的定位要求[19]。

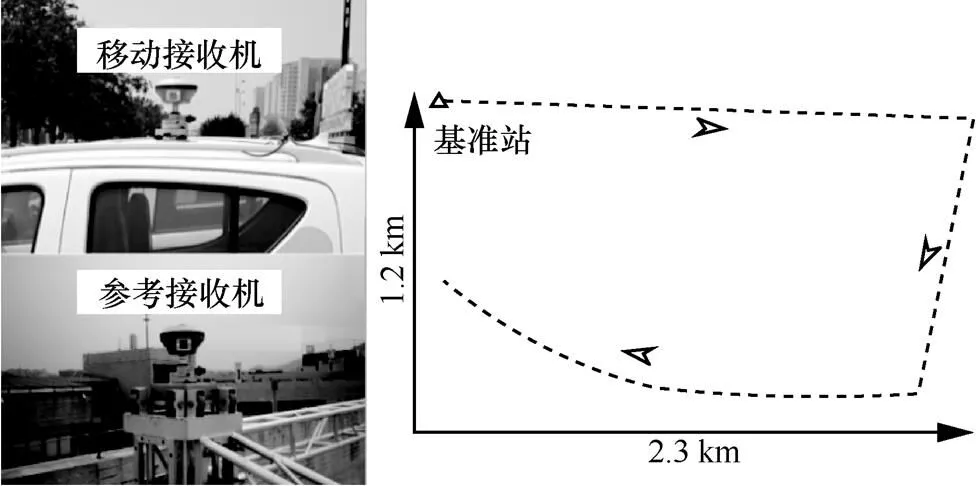
圖3 動態實驗中車輛行駛路線及接收機架設情況

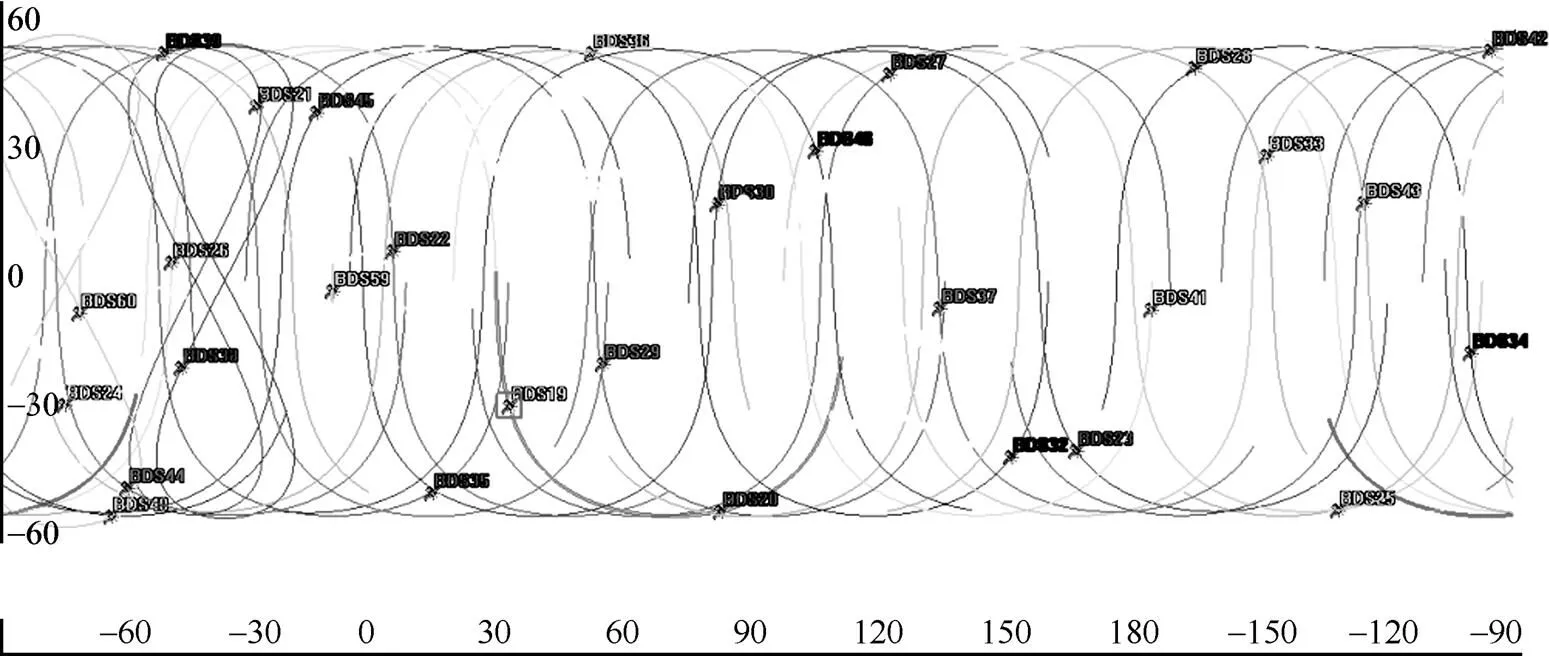
圖4 動態實驗中車輛近似直線運動時北斗三號衛星的星下軌跡

圖5展示了動態實驗中星間、站間、歷元間差分載波相位測速模型解得的參考速度和航向變化。車輛在不同方向的速度均低于15 m/s，U方向速度接近0 m/s，實驗所選道路較為平坦。對應速度參考值曲線可知，航向變化曲線中較為平緩的部分表示車輛行駛于直道或緩彎，陡峭的部分表示車輛急轉，另外，由于本文使用的航向估計方法依賴歷史軌跡，當車輛發生微小位移時航向出現跳變。

動態實驗中原始非差多普勒測速結果和優化非差多普勒測速結果相對于參考速度的誤差如圖6所示，在動態實驗的多數歷元間，優化非差多普勒測速精度高于原始非差多普勒測速。但第150～200歷元間、第500～530歷元間，兩種多普勒測速精度均有明顯下降，其原因是多路徑效應的影響。在第180、290、370歷元附近，優化非差多普勒測速精度反而低于原始非差多普勒測速精度，結合圖5所示航向變化可知，N、E方向速度的大小在這幾個歷元附近發生交替，即車輛轉彎角度大于90°，車輛行駛軌跡的割線方向不能很好地代替切線方向，航向估計出現粗差，因而導致速度解算的約束條件失效。

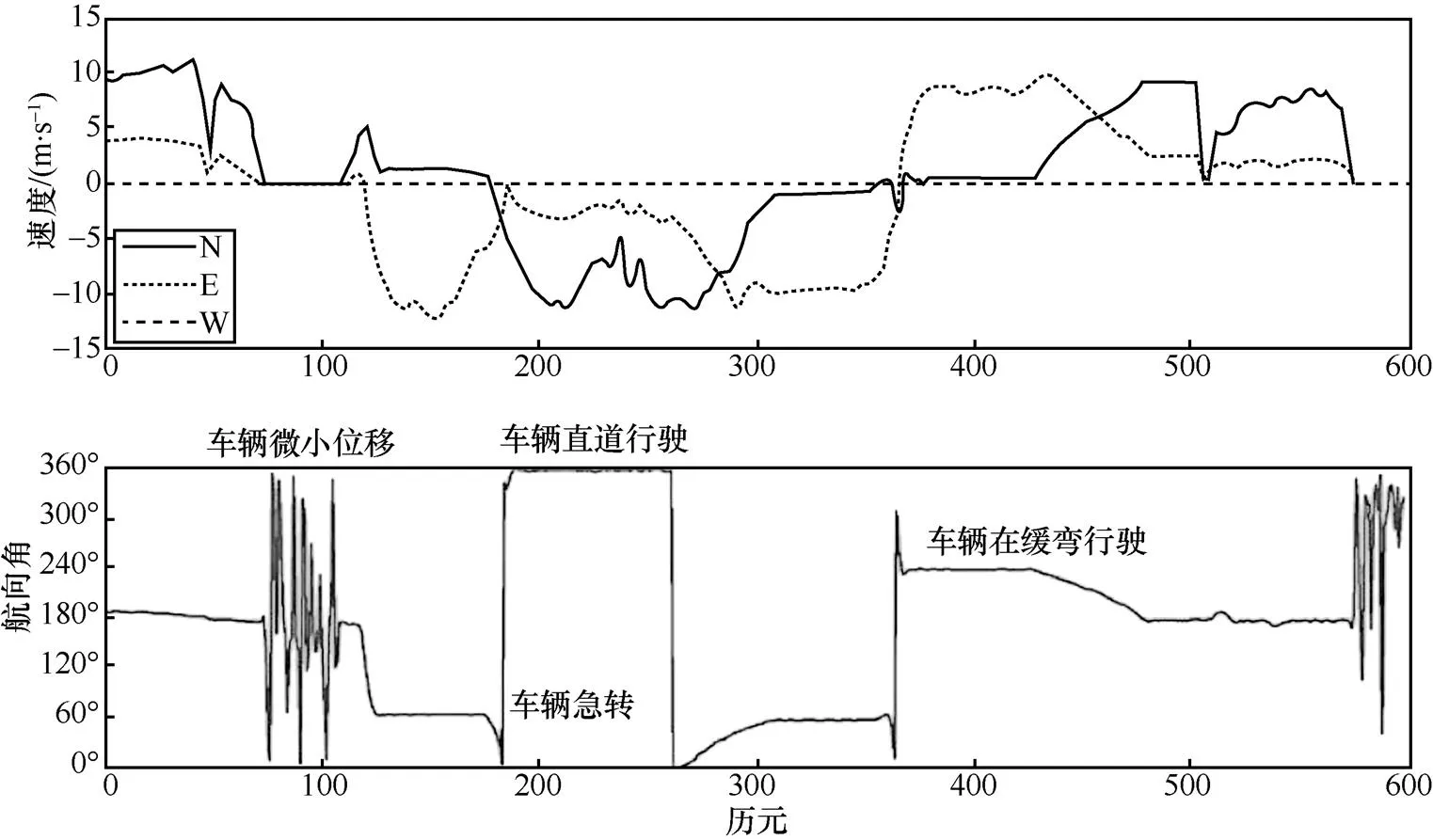
圖5 動態實驗的參考速度和航向變化

動態實驗中兩種方案速度解的誤差對比見表2。在動態實驗中，原始非差多普勒測速模型和優化非差多普勒測速模型的測速精度均為分米級。相比原始非差多普勒測速模型，優化非差多普勒測速精度在N方向上提升了13.8%，E方向上提升了24.6%，U方向上持平。造成N、E方向上精度提升不同的原因是，在實驗所選取的600個歷元間，車輛在E方向上的總體位移大于在N方向上的總體位移，航向約束效果更加明顯。相比靜態測速結果，動態測速在N、E方向的精度提升較小。優化非差多普勒測速解算效率較原始非差多普勒測速解算效率提升了21.9%，與靜態實驗中的效率提升相近，結合圖5所示速度參考值可知，在各個方向速度低于15 m/s的情況下，本文所用的線性化方法適用。

4 結束語

本文提出一種基于北斗三號衛星非差多普勒觀測信號的優化測速模型。對該模型進行靜態和動態測試后，可得如下結論。

（1）載體處于靜止時，優化非差多普勒測速精度相比原始非差多普勒測速精度在N、E方向提升超過60%，在U方向無明顯提升，分析建模原理可知，其原因是航向約束是一種松約束，僅作用于水平速度分量。

（2）載體處于直線行駛或轉彎小于90°時，優化方法可將N方向和E方向的測速精度提升10%～20%，其原因是航向約束顧及了車輛行駛軌跡和速度的相關關系；但當載體轉彎超過90°時優化方法失效，其原因是航向解算有粗差，需要通過提高采樣頻率或改進航向估計方法提升航向精度。

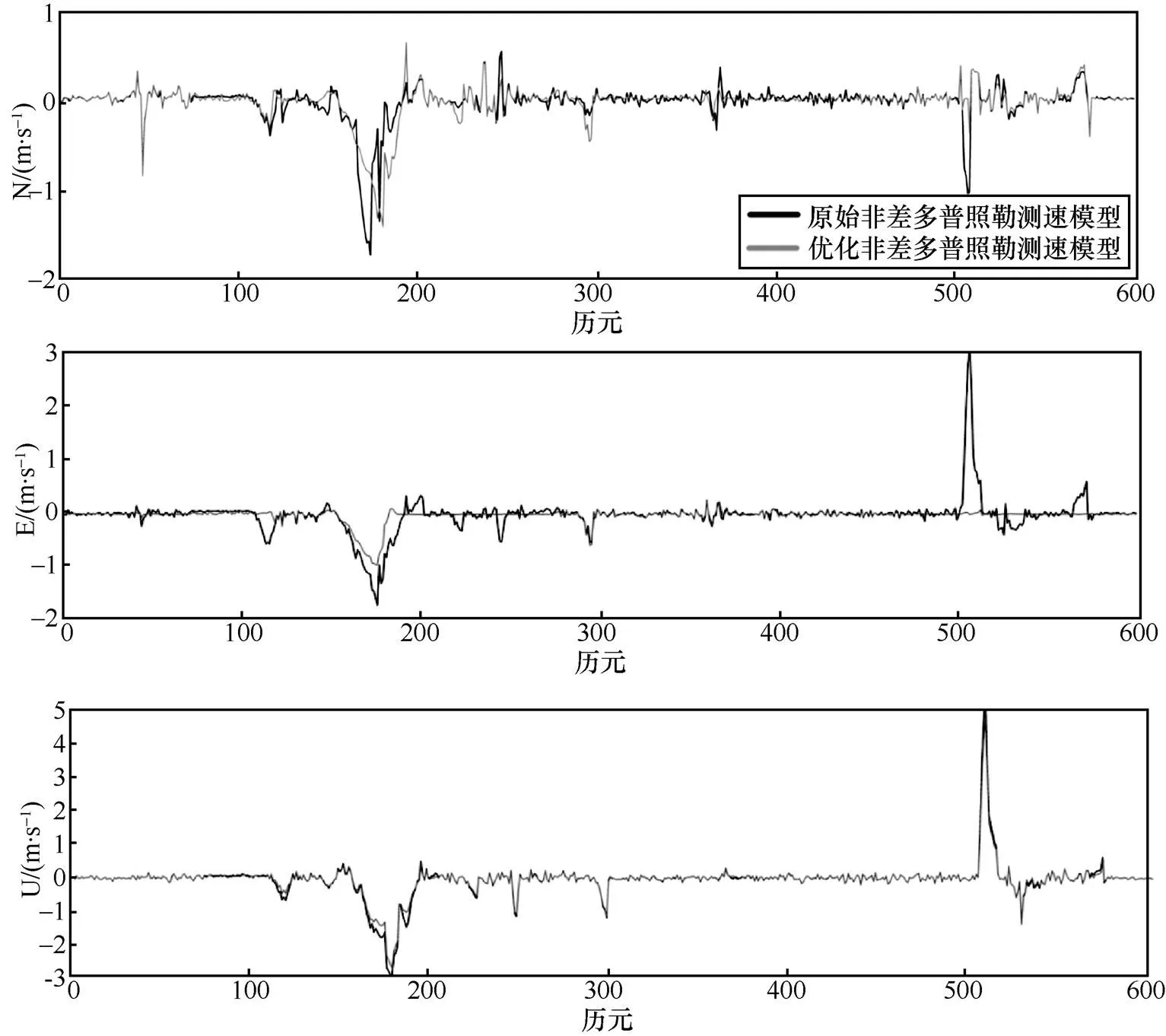
圖6 動態實驗中原始非差多普勒測速誤差和優化非差多普勒測速結果相對于參考速度的誤差

表2 動態實驗中兩種方案速度解的誤差對比

（3）優化非差多普勒測速模型比原始非差多普勒測速模型節省約20%的解算時間，其原因是，通過線性化方法構造的測速模型只需要載體初始位置，之后時刻的載體位置則可通過加入位移求得，故而省略了獨立單點定位的時間，但這種方法可行的條件是：原始多普勒測速模型的構建對載體精度要求較低。

[1] GREENSPAN R L, DONNA J I. Measurement errors in GPS observables[J]. Navigation, 1986, 33(4): 319-334.

[2] 王潛心. 機載GPS動態定位定速與定姿理論研究及軟件開發[D]. 長沙: 中南大學, 2011.

WANG Q X. Research of airborne GPS kinematic position velocity and attitude determination and software development[D]. Changsha: Central South University, 2011.

[3] 姚曜, 張帆, 杜紅松, 等. 聯合多普勒的載波相位精密測速方法[J]. 中國慣性技術學報, 2018, 26(3): 310-315.

YAO Y, ZHANG F, DU H S, et al. Velocity measurement method using carrier phase time-difference with Doppler observations[J]. Journal of Chinese Inertial Technology, 2018, 26(3): 310-315.

[4] WANG Q X. Integrated carrier phase and Doppler observations of GPS and GLONASS for precise velocity determination[J]. 24th International Technical Meeting of the Satellite Division of the Institute of Navigation 2011, ION GNSS 2011, 2011, 3: 2303-2309.

[5] 張輝, 郝金明, 田英國, 等. BDS/GPS接收機系統間偏差穩定性分析[J]. 天文學報, 2017, 58(4): 14-25.

ZHANG H, HAO J M, TIAN Y G, et al. Stability analysis of receiver ISB for BDS/GPS[J]. Acta Astronomica Sinica, 2017, 58(4): 14-25.

[6] 黨亞民, 張龍平, 陳俊勇. 多GNSS系統精密定軌ISB/IFB估計及特性分析[J]. 武漢大學學報·信息科學版, 2018, 43(12): 2079-2084, 2138.

DANG Y M, ZHANG L P, CHEN J Y. ISB/IFB estimation and characteristic analysis with multi-GNSS precise orbit determination[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2079-2084, 2138.

[7] DAI F C, MAO X C. BDS/GPS dual systems positioning based on Kalman filter in urban canyon environments[C]//Proceedings of 17th International IEEE Conference on Intelligent Transportation Systems (ITSC). Piscataway: IEEE Press, 2014: 1882-1883.

[8] 尹瀟, 柴洪洲, 向明志, 等. 歷元間載波相位差分的GPS/BDS精密單點測速算法[J]. 中國慣性技術學報, 2020, 28(2): 226-230.

YIN X, CHAI H Z, XIANG M Z, et al. GPS/BDS precise standalone velocity determination using time-differenced carrier phases[J]. Journal of Chinese Inertial Technology, 2020, 28(2): 226-230.

[9] LI X, GUO J M, ZHOU L. Performance analysis of BDS/GPS kinematic vehicle positioning in various observation conditions[J]. Sensor Review, 2016, 36(3): 249-256.

[10] SOON B K H, SCHEDING S, LEE H K, et al. An approach to aid INS using time-differenced GPS carrier phase (TDCP) measurements[J]. GPS Solutions, 2008, 12(4): 261-271.

[11] 韓松來. GPS和捷聯慣導組合導航新方法及系統誤差補償方案研究[D]. 長沙: 國防科學技術大學, 2010.

HAN S L. Novel GPS/SINS integration architechture and systematic error compensation methods[D]. Changsha: National University of Defense Technology, 2010.

[12] 何海波, 楊元喜, 孫中苗, 等. GPS多普勒頻移測量速度模型與誤差分析[J]. 測繪學院學報, 2003, 20(2): 79-82.

HE H B, YANG Y X, SUN Z M, et al. Mathematic model and error analyses for velocity determination using GPS Doppler measurements[J]. Journal of the Pla Institute of Surveying and Mapping, 2003, 20(2): 79-82.

[13] 王陽陽,王中元,胡超, 等. 優化歷元間載波相位差分的車輛姿態估計模型[J]. 武漢大學學報(信息科學版), 2020: 1-8.

WANG Y Y, WANG Z Y, HU C, et al. Vehicle attitude estimation model using optimized time-differenced carrier phase[J]. Geomatics and Information Science of Wuhan University, 2020: 1-8.

[14] 楊元喜, 楊誠, 任夏. PNT智能服務[J]. 測繪學報, 2021, 50(8): 1006-1012.

YANG Y X, YANG C, REN X. PNT intelligent services[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(8): 1006-1012.

[15] 伍吉倉, 鄧康偉, 陳永奇. 地心坐標系與站心坐標系中的速度轉換及誤差傳播[J]. 大地測量與地球動力學, 2005, 25(3): 13-18.

WU J C, DENG K W, CHEN Y Q. Velocity transformation and error propagation between geocentric coordinate system and site-centric coordinate system[J]. Crustal Deformation and Earthquake, 2005, 25(3): 13-18.

[16] SUN R, CHENG Q, WANG J H. Precise vehicle dynamic heading and pitch angle estimation using time-differenced measurements from a single GNSS antenna[J]. GPS Solutions, 2020, 24(3): 84.

[17] 曾安敏, 楊元喜, 歐陽桂崇. 附加約束條件的序貫平差[J]. 武漢大學學報·信息科學版, 2008, 33(2): 183-186.

ZENG A M, YANG Y X, OUYANG G C. Sequential adjustment with constraints among parameters[J]. Geomatics and Information Science of Wuhan University, 2008, 33(2): 183-186.

[18] 鄭凱, 劉站科, 肖學年, 等. 航空重力GPS測速多粗差探測方法[J]. 測繪學報, 2016, 45(6): 663-669.

ZHENG K, LIU Z K, XIAO X N, et al. Method of multi-dimensional gross errors snooping of GPS velocity estimation in airborne gravimetry[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 663-669.

[19] 耿濤, 丁志輝, 謝新, 等. 基于載波相位差分的多頻多GNSS測速精度評估[J]. 武漢大學學報(信息科學版), 2021:1-11.

GENG T, DING Z H, XIE X, et al. Accuracy assessment of multi-frequency and multi-GNSS velocity estimation with time differenced carrier phase method[J]. Geomatics and Information Science of Wuhan University, 2021: 1-11.

Optimal velocity estimation model based on non-differential Doppler observations from BDS-3 satellites

WANG Zejie1, WANG Qianxin1, SHANG Tianwen2

1. School of Environment and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China 2. State Grid Materials Co., Ltd., Beijing 100054, China

An optimized velocimetric model based on non-differential Doppler observations from BDS-3 satellites with high accuracy and low model complexity was proposed to address insufficient accuracy and low efficiency of velocity estimation method. The observation data from BDS-3 satellites was used to estimate the carrier velocity by using Doppler velocimetric model with low complexity. In order to improve velocity estimation accuracy and solving efficiency, firstly, the model was linearized, and then loose constraints was added based on the correlation between the carrier heading and its velocity vector. The velocity measurement accuracy of the model was verified with field-collected BDS-3 observations, and the applicability of the model was evaluated. The experimental results show that: when the carrier is stationary, the optimized Doppler velocimetry accuracy can reach cm/s or even mm/s level, and in the comparison with the original Doppler velocimetry, the horizontal velocity accuracy was improved by about 60% and the solution time was shortened by 24%; when the carrier is moving, the Doppler velocimetry accuracy with heading constraints can be improved by 14% ～ 21% in north and east compared with the original Doppler velocimetry, and the solution time was improved by about 20%.

BDS-3 satellites, Doppler, heading, loose constrain, linearization

P228

A

10.11959/j.issn.1000?0801.2021267

2021?10?15；

2021?12?10

國家重點研發計劃項目（No.2020YFA0713502）；國家自然科學基金資助項目（No.41874039）

The National Key Research and Development Program of China (No.2020YFA0713502), The National Natural Science Foundation of China (No.41874039)

王澤杰（1994? ），男，中國礦業大學環境與測繪學院碩士生，主要研究方向為衛星定位導航。

王潛心（1980? ），男，博士，中國礦業大學環境與測繪學院教授，主要研究方向為衛星定位導航、大地測量數據處理、衛星遙感。

商天文（1994? ），男，現就職于國網物資有限公司，主要研究方向為供應鏈運營。