海水抽水蓄能電站地下廠房通風熱壓的回歸計算式研究

李建秋，毛宏智

（1.南方電網調峰調頻發電有限公司，廣州 510630； 2.重慶大學，重慶 400045）

引言

隨著全球經濟的快速發展，節約能源與保護環境的需求日益迫切，可再生的清潔能源越來越得到重視。水力發電是重要的清潔能源。抽水蓄能電站利用電力系統負荷低谷電能，抽水至上水庫，在電力系統負荷高峰或需要時再放至下水庫發電，具有調峰填谷、調頻調相、緊急事故備用等多種功能，是當前最高效、最成熟、最環保、最經濟的大規模電能儲存工具之一[1]。

通風對于水電站地下廠房是十分重要的。若地下廠房的通風不當，廠內設備散熱量得不到有效的排除，室內工作環境會變得高溫、悶熱。并且，巖體及部分機電設備會散發出各種有毒有害氣體，通風不當也會對工作人員的健康產生危害。然而，目前大部分抽水蓄能電站地下廠房采用機械通風的方式。相比現有大多數地下廠房采用的機械通風，自然通風能夠減少通風空調系統的初投資與運行能耗，降低電站運營成本[2]。根據現有的研究可知，熱壓是水電站地下廠房自然通風的主要動力[3]。因此，對熱壓的準確預測，有利于水電站自然通風的設計與運營控制，對抽水蓄能電站的可持續建設與運營具有重要意義。

目前對于水電站地下廠房自然通風的研究主要包括實測法、模型實驗法與數值模擬法。張鈺巧[4]通過對某常規水電站自然通風的長期實測，發現電站進風洞末端空氣在單日內的溫度波動小于1℃，并建立了自然通風數學計算模型，分析得到全年不同季節自然通風與機械通風的控制策略。范園園[5]利用相似準則關系式和各種參數的相似比例尺，建立了小灣水電站的等比例物理模型，分別通過冷態試驗與熱態試驗，測試并計算出了各主要通風路徑的阻抗值，且獲得了自然通風量隨季節、運行臺數及室外氣溫的變化規律。肖益民[6]基于網絡模型，提出了水電站地下洞室群各關鍵通道的網絡圖化的方法，并建立了考慮巖體蓄放熱的自然通風網絡模型，用于計算分析水電站地下廠房復雜通風洞室群的全年通風情況。

以上研究均建立了較為復雜的數學計算方法，用于計算電站全年的自然通風變化情況。然而，尚未有研究根據熱壓及其各種影響因素之間的關系，建立用于典型日計算的簡化關系式。并且，熱壓與多種因素之間存在相互作用，這導致無法通過數學推導的方法給出熱壓關于這些因素的顯式表達式。例如，多區域網絡通風模型采用數值迭代的方法，可以計算不同情況下的熱壓值，但是不能直接給出熱壓與各影響因素間明確的定量關系。本文以大萬山海水抽水蓄能電站為例，利用自然通風網絡的方法，通過多元正交組合設計的方法，計算多組參數下的通風熱壓值，并進一步建立熱壓與主要影響因素之間的擬合關系式，從而為其通風設計提供參考。

1 熱壓值回歸計算式的一般形式

1.1 多元回歸法的主要思路

多元回歸是研究一個因變量關于多個自變量的回歸，是反映一種現象或事物的數量依多種現象或事物的數量的變動而相應地變動的規律，建立多個變量之間線性或非線性數學模型數量關系式的統計方法。回歸設計的主導思想是根據試驗的目的和數據分析的要求來選擇試驗點。在所選定的試驗點上安排試驗。這不僅擺脫了被動處理龐大觀測數據的局面。還可以充分發揮各個試驗數據的作用，適當地減少試驗的次數[7]。

因此，在研究熱壓與各因素之間的關系時，可選擇多元回歸的方法，選取多個主要且可控的影響因素，結合多區域網絡通風模型，計算熱壓在這些影響因素多水平條件下的多組值，將結果進行回歸計算，最終給出熱壓值的回歸計算式，即反映熱壓與各影響因素定量關系的顯式表達式。

1.2 大萬山島電站通風路徑與各支路負荷

大萬山島抽水蓄能電站地下廠房與交通洞、出線豎井的縱剖圖如圖1所示。在非事故通風時，交通洞、主廠房出線豎井作為主要的通風路徑。依據自然通風網絡理論，同時將室外大氣環境視為無阻抗的虛擬分支，則其地下洞室的一級通風單回路模型劃分為如圖2所示的結構。圖中，分支1表示交通洞，分支2為主廠房，分支3為出線豎井，分支4為表示室外大氣的虛擬分支。

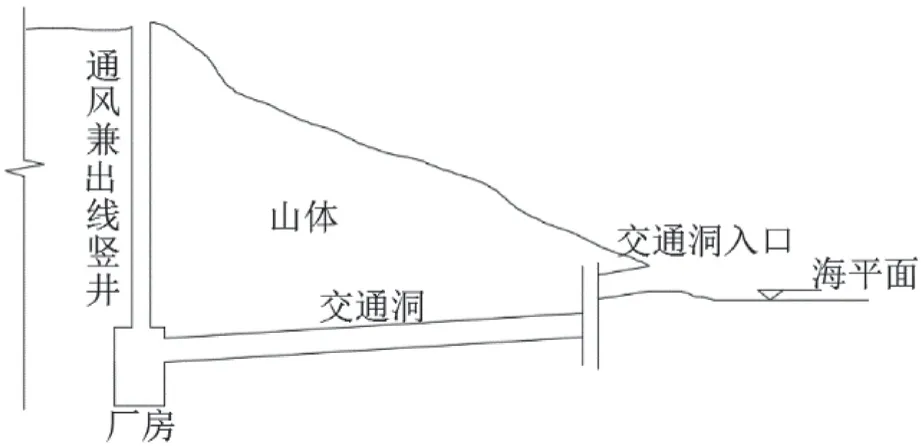
圖1 大萬山島海水抽蓄電站縱剖圖

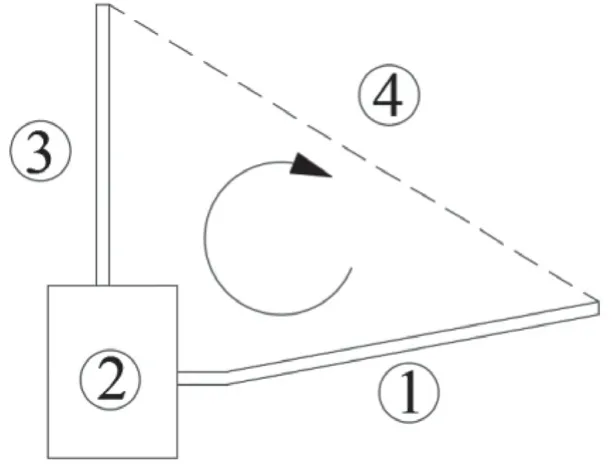
圖2 大萬山島地下洞室通風單回路模型

各洞室的通風流動阻抗及散熱量等信息如表1所示。

表1 各分支主要屬性信息

1.3 熱壓值回歸計算式的自變量選取

1）通風路徑的總阻抗值

各“單元”的阻抗值是反映各洞室、通風隧洞的空間結構尺寸對流動影響的關鍵參數。通風路徑的總阻抗值與熱壓值、空氣密度共同決定了通風量的大小，而通風量又通過影響通風路徑內的空氣溫度分布對熱壓產生影響。并且，海水抽水蓄能電站地下廠房的通風路徑為“一進一出”式，各“單元”串聯連接，各“單元”的通風量是相等的，通風路徑的總阻抗值是各“單元”阻抗值的代數和，不隨熱壓、通風量等體現通風效果的參數發生變化。

因此，通風路徑的總阻抗值可作為一個獨立的因素，用于分析其對熱壓的影響，應作為熱壓回歸計算式的自變量。

2）各“單元”終點與起點的高差

由式（4）～式（8）可知，各“單元”終點與起點的高差將直接影響熱壓值的大小。各“單元”終點與起點的高差由電站結構尺寸所決定，是不隨通風效果發生變化的獨立變量。而主廠房的通風起點即為交通洞的終點，終點即為主廠房與出線豎井的連接處，這兩處結構通常均位于發電機層，其通風起點與終點高度基本一致，故主廠房的高差不作為影響熱壓大小的重要因素。

因此交通洞的高差、出線豎井的高差都是影響熱壓大小的重要因素，應作為熱壓回歸計算式的自變量。

3）各通風“單元”內部散熱量

“單元”內部的散熱量會對進入該“單元”內的空氣產生加熱作用，影響“單元”內空氣的溫度分布，從而影響該“單元”內的熱壓大小。在海水抽水蓄能電站中，各“單元”內部的散熱量應為各隧洞或洞室內，在照明散熱、設備散熱以及空調制冷量三者共同作用下所體現的余熱量。由于通風路徑為“一進一出”式，依照交通洞、主廠房、出線豎井、室外大氣環境被劃分為四個“單元”，而室外大氣環境作為通風耦合計算中的虛擬分支，不對電站通風路徑內的空氣產生傳熱作用。因此影響因素包括交通洞散熱量、主廠房散熱量與出線豎井散熱量。

其中，交通洞內部幾乎沒有連續工作的散熱設備，通常也不設置空調制冷設備，其散熱量主要為照明散熱量。參照NB/T 35008-2013《水力發電廠照明設計規范》，交通洞廊道的照明功率密度為3 W/m2[8]。對于截面寬10 m，長1 km的交通洞，當通風量為10000 m3/h時，照明散熱使得空氣的溫度上升0.0024 ℃，因此交通洞內的照明散熱量對空氣的傳熱作用很小，可以忽略不計。

當主廠房采用空調制冷對交通洞進風進行降溫時，主廠房的散熱量為主廠房內各洞室內的照明散熱量、設備散熱量及空調制冷量三者的代數和。主廠房集中了整個電站絕大多數的散熱設備，其散熱量值較大，且隨電站運行工況的切換具有較大幅度的變化，對空氣溫度變化與熱壓的大小具有重要影響。

出線豎井內一般不單獨設置空調制冷設備，因此出線豎井內的散熱量包括豎井內的照明散熱量與出線電纜及相關設備的散熱量。這兩部分的散熱量通常與出線豎井的長度呈正比例關系。由于出線豎井具有較大的高差，內部散熱量的變化將使熱壓發生變化，因此當海水抽水蓄能電站出線豎井的電纜每米散熱量與照明功率密度是固定量時，豎井的散熱量值通常與豎井的高差成正比關系，可在熱壓值回歸計算式中忽略散熱量這個自變量，它對熱壓的影響仍可通過出線豎井高差這個自變量反映出來。

需要說明的是，在實際上，圍護結構對空氣的傳熱量也應是各“單元”內部散熱量的組成部分，對各“單元”內的空氣溫度產生直接影響。但是，圍護結構對空氣的傳熱量受到季節、室外空氣溫度以及通風量等因素的影響，其大小不宜作為某一固定值直接計入各“單元”散熱量的計算，宜分季節進一步討論。因此，圍護結構對熱壓的影響將作為單獨的影響因素進行考慮。

4）圍護結構對空氣的傳熱作用

圍護結構對空氣具有傳熱作用，且圍護結構具有周期性的“蓄熱”“放熱”變化規律。圍護結構對空氣的傳熱量會影響空氣的溫度大小，進而影響“單元”內的熱壓大小，是影響熱壓大小的重要因素。

然而，在電站通風設計期，圍護結構對空氣的傳熱量大小是不確定的。該值除了與設計地點的巖石熱物性參數、通風量有關外，還會受到計算時刻之前歷史時刻內的通風傳熱情況的影響，且這種影響具有時間上的累積性。因此圍護結構對空氣的傳熱量只能通過模擬計算足夠長時間段內的通風情況之后確定，難以在設計初期直接取值。同時圍護結構傳熱量可由熱流密度與換熱面積的來表示。

因此，不選取圍護結構的傳熱量直接作為自變量，而是通過用各洞室換熱面積作為自變量，并且按照四季不同、晝夜不同分別計算熱壓值及通風效果的方式來減小圍護結構傳熱的預測誤差。

5）室外空氣溫度

一方面，室外空氣溫度對交通洞內的圍護結構傳熱量大小具有顯著影響，另一方面，根據式（3）～式（8），室外空氣溫度會影響室外空氣密度，進一步對熱壓的大小產生影響。因此，室外空氣溫度也是影響熱壓大小的重要因素。

6）通風量

即使其他條件均相同，通風量的變化也會改變各分支單元內的空氣溫度，空氣溫度變化又會引起熱壓值的變化。此外，熱壓、通風量、風機壓力之間還存在式（1）的平衡制約關系。

式中：

Pj—風機壓力，Pa；

G—通風量，kg·s-1。

因此，通過上面的分析可發現，通風量作為熱壓值的重要影響因素，應在熱壓值回歸計算式中作為自變量予以考慮。

1.4 熱壓回歸計算式的形式

總結適用于各種結構尺寸的海水抽水蓄能電站通風熱壓值回歸計算式，自變量應包括：通風量G、通風路徑的總阻抗值U、主廠房散熱量Q2、交通洞高差H1、出線豎井高差H3、室外空氣溫度Tw、交通洞、主廠房以及出線豎井的換熱面積A3。熱壓值回歸計算式的形式為式（2）：

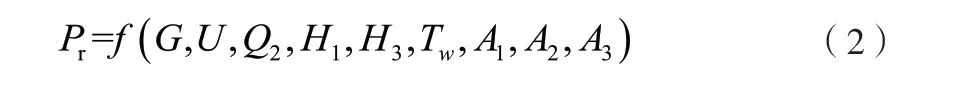
式中：

Q2—主廠房散熱量，kW；

Q3—出線豎井散熱量，kW；

H1—交通洞終點與起點高差，m；

H3—出線豎井終點與起點高差，m；

Tw—室外空氣溫度，℃；

A1—交通洞內表面換熱面積，m2；

A2—主廠房內表面換熱面積，m2；

A3—出線豎井內表面換熱面積，m2。

對結構尺寸已經確定的海水抽水蓄能電站，則交通洞高差H1、出線豎井高差H3、交通洞內換熱面積A1、主廠房內換熱面積A2、出線豎井內換熱面積A3則為固定值。自變量則為：通風量G、主廠房散熱量Q2、室外空氣溫度Tw。熱壓值回歸計算式的形式為式（3）：

2 日平均熱壓值的多元二次回歸正交組合設計

二次回歸正交組合設計是指回歸模型中包括常數項、線性項、線性交互作用項及二次項的回歸正交設計。相比一次回歸正交設計，二次回歸正交組合設計多引入了二次項，能進一步提高回歸計算式的精確性[7]。

二次回歸正交組合設計所安排的因子空間中不同類型的試驗點一共有3類：第一類是按照二水平正交表所安排的試驗，形象的稱為正交試驗點；第二類是零水平處的重復試驗，形象地成為中心點；第三類是根據參數γ的值令編碼x1，x2，x3，x4中的一個為γ，其余的為0，所安排的試驗被稱為星號點。

設自變量的個數為p，對于p個自變量的組合設計則可由以下3類共計mc+2p+m0個試驗點組合而成。①由二水平的全因子試驗計劃或部分實施計劃所決定的mc個試驗點，這里的mc=2p，2p-1，2p-2，…；②分布在p個坐標軸上由星號臂γ所決定的2p個星號點，這里的星號臂γ是星號點到中心點的距離，可以根據正交性與通用性的要求進行選擇；③m0個中心點，m0=1，2…。

為了保證二次回歸組合設計的正交性，必須使新引入的平方項中心化，并根據點試驗的次數m0選擇星號臂γ的數值。即用的離均差代替，計算計算式為式為式（4）：

二次回歸正交組合設計的步驟與一次回歸正交設計類似，即先找到各個自變量的變化范圍，確定各個自變量的上界、下界、零水平及變化半區間。零水平按照式（6）計算，變化半區間計算計算式如式（7）：

之后，對各個自變量的水平進行編碼，也就是對自變量zj變化的下界z1j和上界z2j作線性變換，令，使z0j變換為0，z1j變換為-γ，z2j變換為γ，變換為-1，z0j+Δj變換為1。

編碼后，y對z1，z2，…，zp的回歸問題就轉化為y對編碼x1，x2，…，xp的回歸問題。為取得y的模擬計算值，建立回歸計算式，便要在一個以x1，x2，…，xp為坐標的編碼空間中選擇試驗點，進行試驗設計。

之后，可根據自變量以及它們之間必須加以考慮的交互作用的個數，選擇適當的二水平正交表，根據正交表確定試驗點并取得y的觀測值，建立y對x1，x2，x3，x4的線性回歸計算式，最后再將zj與xj的關系帶入計算得到的線性回歸計算式，得到二次回歸計算式。

對此次大萬山島海水抽水蓄能電站冬季通風熱壓日平均值的二次回歸計算，自變量仍為通風量z1（kg/s）、主廠房散熱量z2（kW）、出線豎井高差z3（m）與室外空氣溫度z4（℃）的下界、上界、零水平及半區間的數值如表2，并作線性變換，。

表2 二次回歸設計四變量的z1j，z2j，z0j及△j

在模擬計算中，通風量可以通過開啟風機或減小通風路徑上的風閥等措施進行調節，主廠房散熱量也可通過開啟空調制冷進行調節，出線豎井的高差也可以在設計初期進行適當調整，因此，可以通過-γ，γ，0,1，-1的比例關系計算確定這四個自變量的值，代入模擬計算程序，計算相對應的全年逐日或典型日逐時的通風情況。但是，全年逐日或典型日逐時的室外空氣溫度是根據設計地點確定的，而且圍護結構對空氣的傳熱量與計算時刻前的相當長一段時間的傳熱情況有關，人為改變某一日的室外空氣溫度計算值會導致計算結果失真。因此，在進行二次回歸的正交設計時，室外溫度的數值應在深圳氣象參數的12.1～2.28這一段時間內的日均溫度中選取。這一段時間的日均溫度分布見圖3。按照二次回歸的正交設計，當-γ，γ兩水平的室外溫度取值分別為8.70與22.41時，-1、0、1水平所對應的溫度值應為10.71 ℃、15.56 ℃、20.40 ℃。根據深圳氣象參數，只有在1月14日、2月7日、12月18日時的日均溫度為10.60 ℃、15.52 ℃、20.16 ℃最接近回歸正交設計所需值，溫度值的絕對誤差最大為0.24 ℃，因此可忽略室外溫度取值誤差對熱壓值計算的影響。

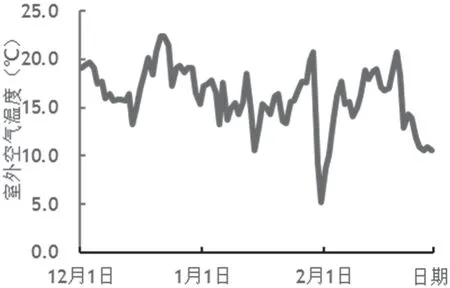
圖3 深圳12.1～2.28室外空氣溫度變化值

根據正交表L16(215)的前四列的16個正交試驗點、根據參數γ計算的8個星號點以及零水平處1個中心試驗點共25組自變量取值方案安排模擬計算，各方案的熱壓值y（Pa）的模擬計算值如表3。

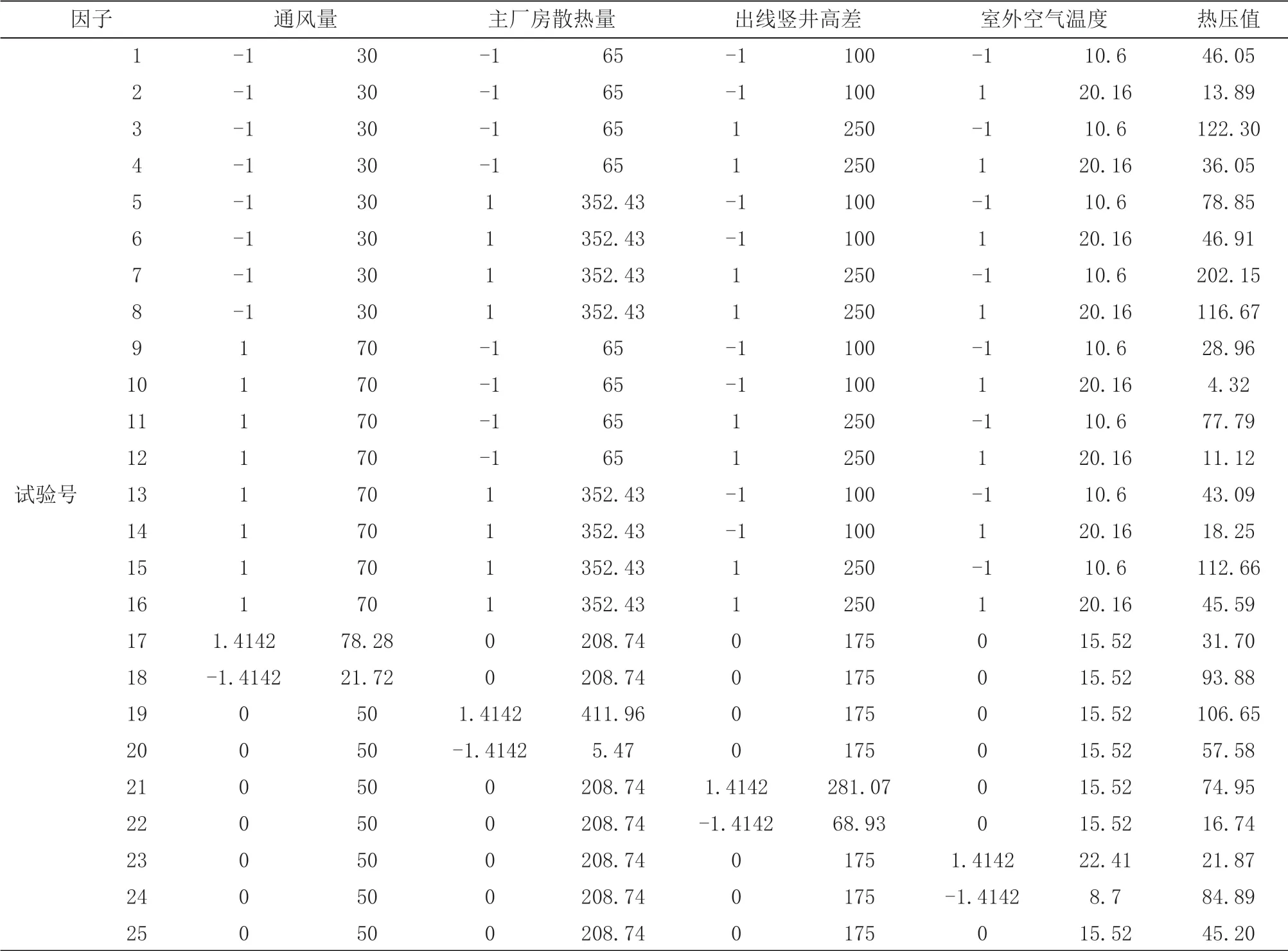
表3 二次回歸正交試驗安排及熱壓值y的模擬計算值

根據試驗模擬計算的結果，計算四元線性回歸計算式得到式（8）：

對回歸方程進行顯著性檢驗：

方差檢驗F=60.877，顯著性水平α=1-9.14×10-8，決定系數R2=0.970，調整后的決定系數Ra2=0.970，該計算式顯著。

為了進一步提高熱壓值回歸計算式的顯著性水平，可對回歸系數進行顯著性檢驗，逐一地排除顯著性最差的回歸系數，在每排除掉一個回歸系數之后，需要對回歸計算式重新進行顯著性檢驗。直到在排除某個回歸系數之后，回歸計算式的顯著性下降，則該回歸系數及其他回歸系數不應被排除，最終的回歸計算式即為包括此回歸系數項的計算式。

對式（8）中的各個回歸系數進行分析，依次排除顯著性最差的回歸系數的項，即

最終得到的基于深圳設計地點的大萬山島海水抽水蓄能電站冬季自然通風日平均熱壓值回歸計算式為式（9）。

式（9）的決定系數R2=0.988，調整后的決定系數。

同理，基于深圳為設計地點的大萬山島海水抽水蓄能電站地下廠房春季、夏季、秋季的通風熱壓值日平均回歸計算式，以及以上海為設計地點的結構尺寸及布置情況相同的海水抽水蓄能電站地下廠房四季的通風熱壓日平均值回歸計算式見附錄。

3 熱壓值回歸計算式對通風設計與運行控制的指導作用

根據回歸計算式可以指導海水抽水蓄能電站的通風設計與運行控制策略的制定。

在規范中對水電站主廠房的排風溫度也有上限值的要求[2]，因此，主廠房排風溫度Tp與通風量均是通風控制策略中的重要控制指標。主廠房排風溫度Tp不應超過限值的要求。

主廠房排風溫度取決于主廠房送風溫度、通風量與主廠房散熱量，計算關系如式（10）。

式中：

Tp—主廠房排風溫度，℃；

Tj—交通洞終點處空氣溫度，℃；

cp—空氣定壓比熱容，kJ/(kg·℃)。

主廠房送風溫度即為交通洞終點處的空氣溫度，它又取決于室外空氣溫度、通風量與交通洞圍護結構對空氣的傳熱量。

綜上所述，在海水抽水蓄能電站地下廠房通風設計時，應優先保證主廠房排風溫度在限值以內，結合通風量與室外空氣溫度，確定主廠房空調制冷量和排入通風氣流的散熱量；再結合出線豎井排風溫度及室外空氣溫度，計算出各時刻的通風熱壓值。進一步根據熱壓值與通風總動力需求值的關系，確定通風控制措施。在海水抽水蓄能電站通風實際運行時，應對排風溫度和通風量進行監測，根據情況進行相應的實時調控。

4 結論

1）對影響熱壓的各因素進行了分析，闡述了各個因素作為通風熱壓回歸計算式自變量的適宜性，總結了通風熱壓回歸計算式的形式。

2）以大萬山海水抽水蓄能電站在冬季按照需求通風的方案為例，以通風量、主廠房散熱量、出線豎井高差及室外空氣溫度為自變量，計算了日平均熱壓值的多元二次回歸計算式，發現多元二次回歸計算式可以滿足顯著性檢驗。

3）選擇二次回歸正交組合設計的方法，以深圳為設計地點，建立了大萬山抽水蓄能電站各個季節的熱壓回歸表達式，并從提高計算式顯著性的角度，對顯著性較低的系數項進行了刪減。回歸關系式可用于對應條件下各個季節的熱壓簡化計算。本文建立熱壓回歸計算式的方法，可供類似地下廠房工程參考。