高低溫環境試驗箱冷負荷敏感性分析

吳昊，龍鐵明

（1.西安交通大學能源與動力工程學院，西安 710000； 2.廣東瑪澳環境試驗設備科技有限公司，東莞 523000）

引言

在高低溫環境模擬儀器設備中，為了簡化冷負荷計算過程，一般采用穩態傳熱計算，工程經驗認為內箱體及箱體圍護結構對冷負荷影響較大，但是缺乏定量分析的理論依據，穩態傳熱模型無法精確計算對流情況下的換熱過程，往往使得計冷負荷算結果偏大，并造成壓縮機選型過大。因此冷負荷的準確計算對于環境試驗箱的節能設計具有重要的意義。

在國內方面有學者針對試驗箱冷負荷做了以下研究，張征鴻[1]認為試驗箱的冷負荷不由穩態降溫所確定，而是由非穩態時在設計降溫速率下的冷負荷所確定，并進行了驗證。王芳[2]采用工程試驗方法對維護夾層的降溫速率進行了測定，對降溫速率與制冷設備的匹配提出了建議。吳志勇[3]采用一維非穩態傳熱模型對圍護漏冷進行計算，結論表明在給定設計降溫速率的情況下，圍護結構對冷負荷貢獻最大。

在氣動設計領域中，為了減少較多設計變量時的流場分析時間，常采用伴隨方法[4]（Adjoint method）對設計變量進行敏感性分析，伴隨方法本質上是一種自動微分方法，可以通過一次流場求解與一次敏感性求解，快速得出目標函數對所有設計變量的敏感性。

本文采用自動微分算法，基于穩態傳熱模型，分析了冷負荷對于多個箱體設計變量的敏感性，并采用非穩態對流傳熱方法進行驗證，討論了不同內箱壁厚及制冷量對降溫過程的影響，揭示了環境試驗箱在降溫過程中的傳熱學機理，所采用的方法為環試設備的節能設計提供了一定參考。

1 穩態傳熱計算

以某防爆驗箱為研究對象，對其進行穩態冷負荷分析，需求如下：

1）內箱體尺寸：W1000*H1500*D1500；

2）溫控范圍：25～200 ℃；

3）降溫速率：＞2 ℃/min；

4）負載情況：200 kg鋁塊，無發熱；

5）內箱材料：SUS304不銹鋼，厚度 5 mm。

經初步設計后，確定空調箱深度180 mm，幾何模型如圖1所示。

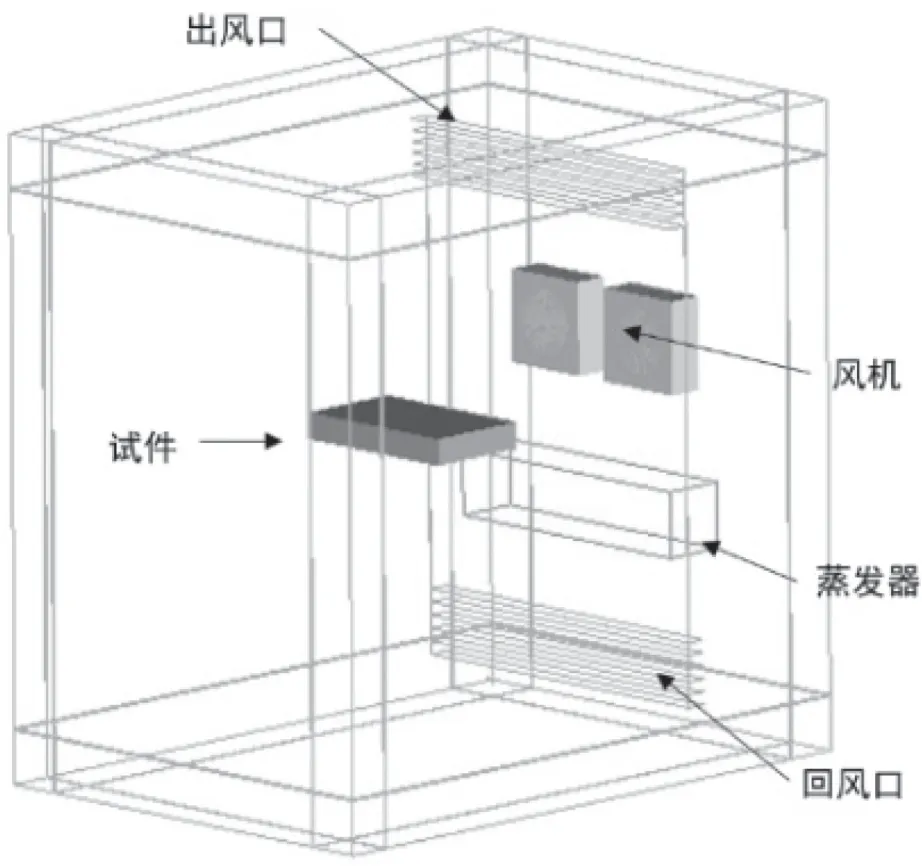
圖1 三維模型及主要部件

對該方案進行穩態冷負荷計算[5,6]，降溫速率按照2.5 ℃/min計，過程如下：

1.1 箱體空氣循環負荷

式中：

Vbox—內箱體體積；

ρair—空氣密度；

Cair—空氣比熱容；

DT1—最高最低溫差；

Thour—降溫小時數。

1.2 箱體結構冷負荷

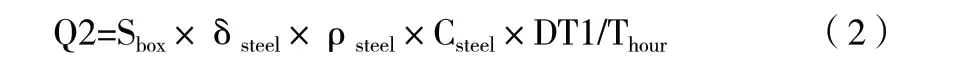
式中：

Sbox—內箱體表面積；

δsteel—內箱體鋼板厚度；

ρsteel—鋼板密度；

Csteel—不銹鋼板比熱。

1.3 圍護結構漏冷冷負荷

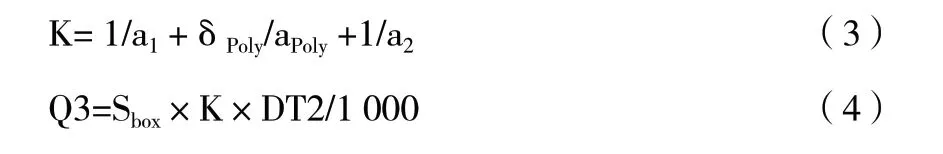
a1—外壁傳熱系數；

a2—內壁傳熱系數；

δPoly—保溫層厚度；

aPoly—保溫層傳熱系數；

Sbox—內箱體表面積；

DT2—箱外溫度與最低溫差。

1.4 被測試件冷負荷

Mal—鋁塊重量；

Cal—鋁比熱；

DT3—被測件內部降溫溫差。

1.5 蒸發器部件冷負荷

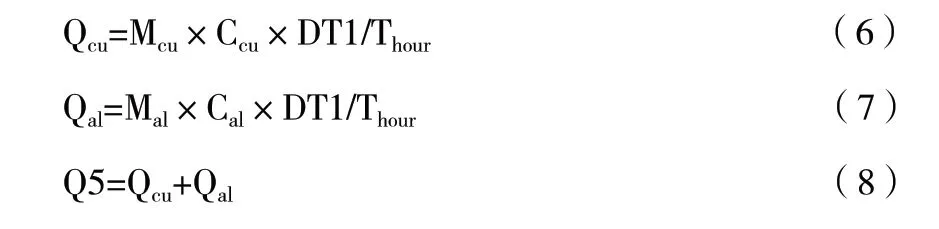
Qcu—銅管冷負荷；

Qal—鋁翅片冷負荷；

Mcu—銅管質量；

Mal—鋁翅片質量；

Ccu—銅管比熱；

Cal—鋁翅片比熱。

1.6 其余部件冷負荷

其余部件包括風機馬達發熱：

加熱管材料冷負荷：

風機主軸材料冷負荷：

試品架冷負荷：

Pm—風機馬達功率；

Nm—風機馬達數量；

ηm—馬達熱效率；

Mh—加熱管質量；

MA—風機主軸質量；

Ms—試品架質量。

1.7 總冷負荷

經計算可得總冷負荷為23.43 kW，其中內箱體及圍護部分貢獻冷負荷11.57 kW，占總冷負荷的49.39 %。

2 自動微分算法

自動微分算法可以根據計算機程序自動生成導數計算程序，其理論是以鏈式求導法則為基礎，自動微分可以分為前向模式與后向模式兩種，根據給定的設計變量a，目標函數f，前向模式給出了其方向導數△f·a，后向模式則給出了梯度△f，本文采用后向模式，一次性求出目標函數對各個變量的梯度。

針對設計變量a，中間變量x，及目標函數f存在如下關系：

根據上述定義，目標函數f對設計變量a的敏感性可通過下式計算：

3 穩態傳熱敏感性分析

通過（18）式對式（14）的22個設計變量進行自動微分，得到各個變量的敏感性如表1所示。

根據表1，對敏感性排名前5位的設計變量進行降序排列，可得表2。

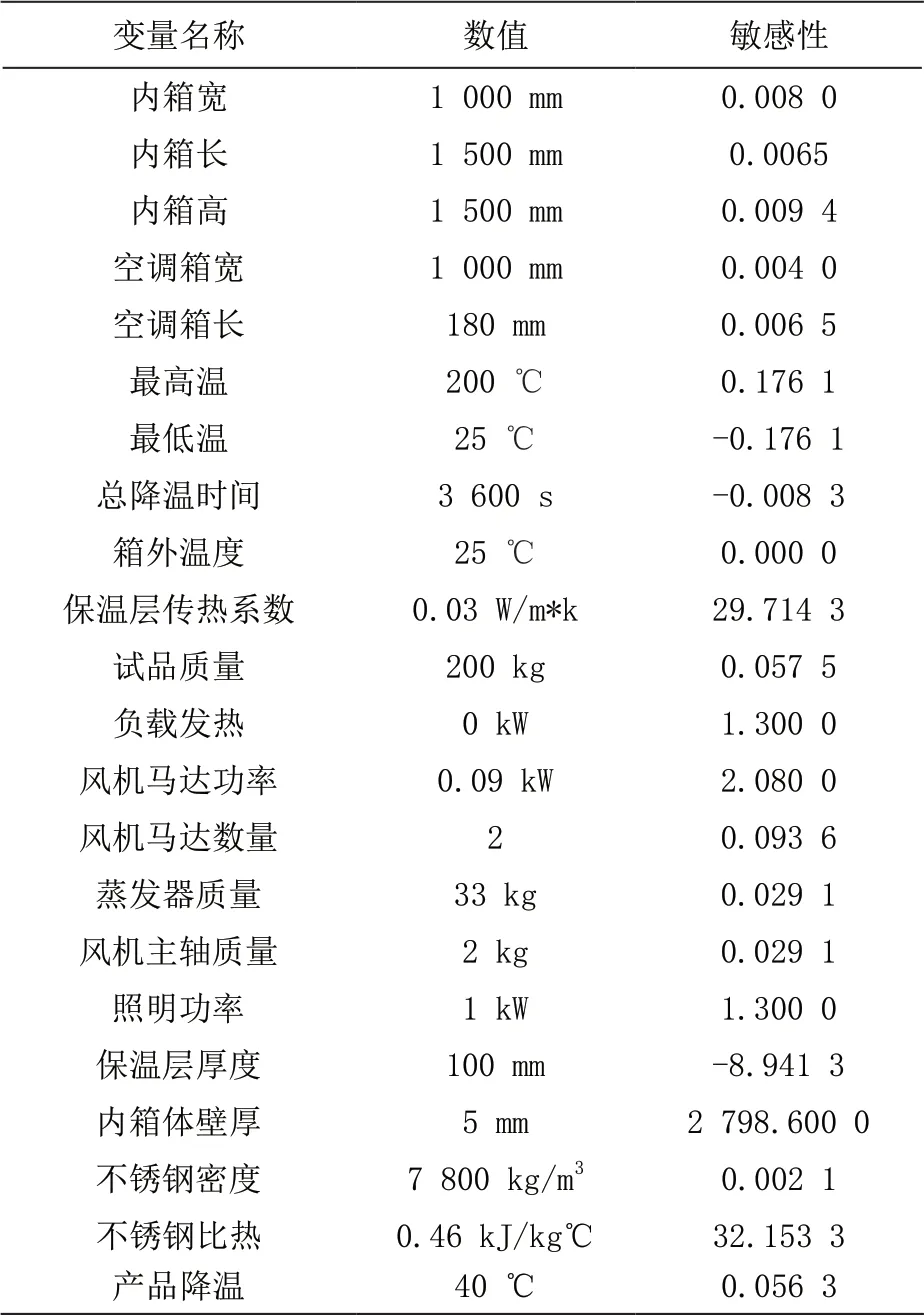
表1 設計變量數值及敏感性

由表2可以看出，冷負荷對內箱體壁厚的敏感性巨大，達到2798.60，是第二位不銹鋼比熱容的92.64倍，是第三位保溫層傳熱系數的100.25倍。

表2 敏感性排名前5位的變量

通過以上分析可以得出結論，內箱體壁面的熱容效應是阻礙降溫的主要因素，其中不銹鋼材料內箱壁厚對冷負荷的敏感性達到2798.60，即在穩態計算中，內箱壁厚度增加1 mm會造成冷負荷增加2.798 kW。

4 非穩態流動傳熱分析

雖然在穩態傳熱過程中也考慮循環空氣量的冷負荷，但并未考慮對流效應對傳熱的影響，只是將空氣與壁面的傳熱過程當作穩態傳熱過程對待，雖然在近壁面區域由于空氣邊界層的原因，傳熱過程近似于穩態傳熱，但是由于箱內空氣的對流傳熱過程非常復雜，一般的集總參數法無法準確計算箱體內的對流傳熱過程。

通過求解流體力學中的質量守恒方程，動量方程，能量方程[7]，可以較為準確地模擬內箱體的對流傳熱過程。

根據產品三維模型進行CFD分析，考慮到內箱體壁的溫度梯度，同時為捕捉壁面空氣側邊界層的流動，對箱體內壁至空氣側的計算域網格進行加密，為減少網格量，蒸發器為不帶翅片的實心光管模型，計算域網格如圖2所示。

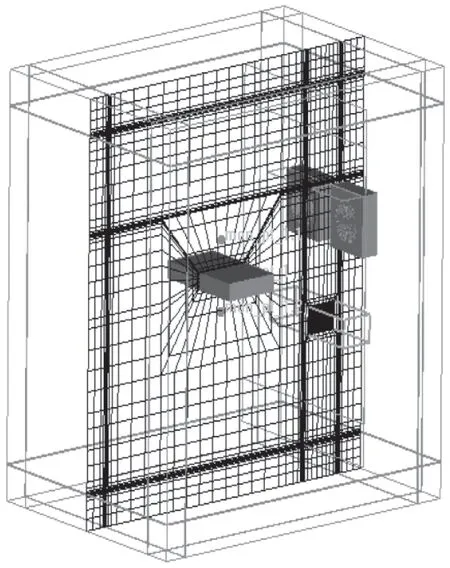
圖2 計算域網格及溫度監控點示意

溫度監控點共三個，分別位于試件中心的point1及試件的上下方point2，point3，位置距試件中心上下80 mm處。空氣采用Boussinesq近似，風機模型以P-Q曲線給定，采用K- ωSST湍流模型。輻射計算采用DO模型。全計算域內初始溫度200 ℃，時間步長1 s，給定蒸發器制冷量8 kW，共進行3600 s的非穩態計算，整個計算過程收斂良好，得到溫度分布如圖3。

由圖3可以看出，整個箱體保溫層中心區域溫度保持在200 ℃基本沒有變化，從保溫層區到內箱壁區域溫度過渡均勻緩慢，溫度梯度較小，從內箱壁到空氣區域的溫度梯度較大，這是由于該部位空氣側的對流傳熱系數遠高于材料側的傳熱系數所致，經過探針拾取溫度，可得相同間距內，內箱壁中心區域與空氣側溫差是內箱壁中心區域與保溫層側溫差的1.6～2倍。

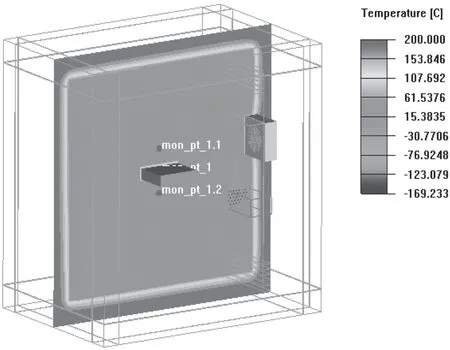
圖3 3600 s時的溫度分布

使用實心銅管代替蒸發器銅管，給定銅管制冷量后，根據熱傳導方程計算得到制冷量所對應的區域溫度，由于不帶翅片，傳熱面積大大降低，使得空氣溫度與蒸發器溫度溫差巨大，最低溫區域位于銅管中心，達到-169 ℃，但考慮到帶翅片后由于蒸發器傳熱面積增大，則降溫速率應大于光管情況，故作為保守預估的情況，采用光管蒸發器模型計算冷負荷是可行的。監測點降溫曲線如圖4。

圖4顯示出試件上下方空氣區的監測點溫度差很小，均從200 ℃下降到45 ℃左右，雖然未達到25 ℃的目標溫度，但是8 kW制冷量已經非常接近實際需求制冷量。前300 s內降溫速率較快，接近8 ℃/min，后3300 s內降溫2速度放緩至2.09 ℃/min，這是由于前期流場不穩定造成的，后期隨著流場趨于穩定，降溫速率也趨于穩定。全程降溫速率＞2 ℃/min，滿足設計需求。全流場計算已經考慮到內箱體放熱、圍護漏冷、空氣循環量、蒸發器質量4個發熱源，再加風機發熱、加熱管質量及馬達軸心質量的冷負荷，考慮到安全余量，則蒸發器取12 kW的制冷量較為合理，與穩態計算的23.43 kW相比減少48.7 %。

圖4 監測點的降溫過程

若改變內箱壁厚，分別采用4 mm，6 mm內箱壁厚進行仿真，得到溫控點的降溫曲線如圖5所示。

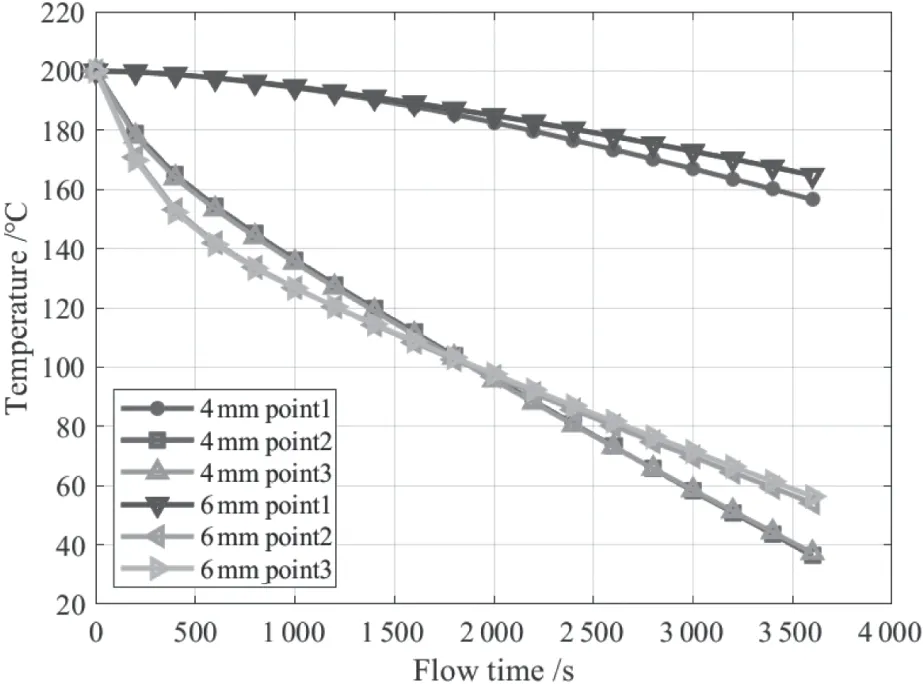
圖5 不同內箱壁厚的降溫曲線

從圖5中可以看出，同樣經過3600 s的降溫時間，隨著內箱壁厚的增大，空氣側最低溫度逐漸上升，采用4 mm內箱壁厚時，試件中心溫度降至155 ℃，空氣溫度降至（36～37）℃。采用6 mm內箱壁厚時，試件中心溫度降至164 ℃，空氣溫度降至（56～58）℃。4 mm內箱壁厚的降溫速率更加接近線性過程，全程接近2.71 ℃/min。若采用6 mm內箱壁厚方案時，前500 s內的降溫速率接近6 ℃/min，后3100 s的降溫速率接近1.96 ℃/min。這是由于內壁增厚時會在高溫階段吸收更多的熱量，這些熱量將在降溫階段大量釋放。

5 非穩態傳熱敏感性分析

若將內箱壁厚Dth看成一個與蒸發器制冷量P相關的函數，則制冷量在內箱壁厚5 mm處的前向敏感性可以表示為:

式（19）可以通過差分格式求解，壁厚Dth步長取1 mm，制冷量P步長取1 kW，得到?P/?T項為0.054，即最低溫降溫1℃相應的制冷量需要提高0.054 kW，?T/?Dth項為10.2，即內箱壁厚度增大1 mm，空氣側終點溫度將升高10.2 ℃，并可得△?P·Dth為0.55，即增大內箱壁厚1 mm，相當于增加冷負荷550 W。結合表1，可以看出，即使非穩態計算時的內箱壁厚敏感性有所降低，但仍舊遠遠大于保溫層敏感性的-8.94、風機馬達功敏感性的2.08、以及負載及燈具發熱敏感性的1.3。

6 結論

本文根據采用自動微分算法，基于穩態傳熱模型，對箱體22個設計變量的冷負荷進行了敏感性分析，又通過全三維非穩態對流傳熱模型，計算了不同箱體壁厚及制冷量對冷負荷的影響，由分析可得以下結論：

1）動態冷負荷較穩態冷負荷計算偏小48.7 %，差異主要在于對于內箱壁面對流傳熱效應的計算方式不同，在今后的研究中，應考慮產品發熱對箱體冷負荷的影響做進一步分析。

2）制冷量最大需求主要在于降溫階段，保溫階段的制冷量主要用于平衡一部分的箱體剩余熱容及環境漏熱。

3）降溫速率越大，箱體尺寸越大，箱體的熱容效應越顯著，穩態計算誤差越大，故基于穩態的箱體冷負荷計算應慎重使用，實際設計過程中應結合實驗數據進行修正。