基于SPH 粒子化的重心變化模型研究
孫一凡,崔 杰,張寧寧,王天宇,趙乾宇,代雨辰
(沈陽航空航天大學理學院,遼寧 沈陽 110136)
0 引言
本文圍繞實際生活中的水箱問題進行相關的研究。已知長方體以及兩固定水箱的長度、寬度等幾何參數,給定長方體始態“平放”和終態“豎放”的放置方式。探究注入水箱中水的比例不同(兩水箱的比例是相同的)對于長方體的形心與重心位置變化關系的影響[1-2]。同時為了能使長方體在“平放”到“豎放”過程中,形心與重心之間的距離最小,分別探究兩個固定水箱共同的傾斜角度和兩個水箱斜放角度不同時的情況,找到最合適的傾斜角度。
1 重心軌跡模型構建
左下水箱邊長長度關系:
將左下水箱向上轉動φ 角度,主視圖如圖1、圖2 所示,水箱內虛線為最開始的水平面,黑色實線為水平面,高于初始水平面的水量為初始虛線下的黑色實線上的水量的移動[3-5],選取原始水平面中點,通過研究該點的運動軌跡來反映整個水箱轉動過程的運動方程。
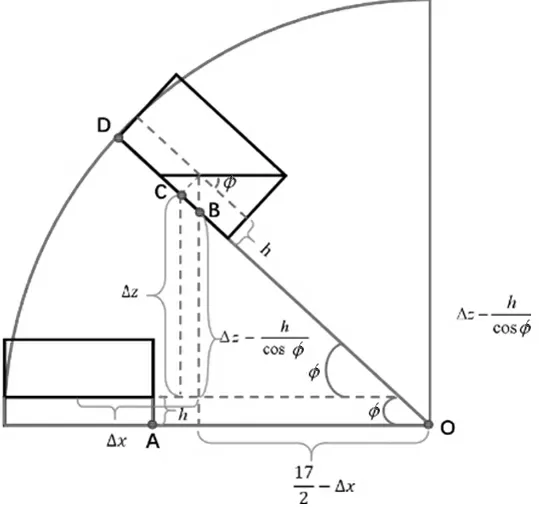
圖1 左下水箱轉動φ 角度
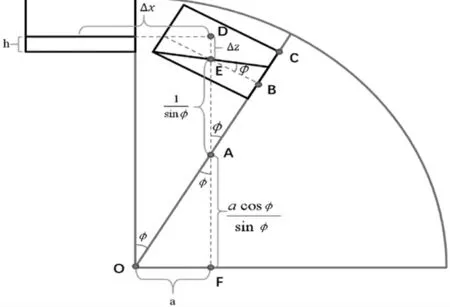
圖2 右上水箱轉動φ 角度
半徑長度一定得到的條件,見式(1)、式(2)。

其中:h1——初始水位;Δx——代表點x 軸坐標增量。
利用角度得到的條件,見式(3)、式(4)。

右上水箱邊長長度關系,見式(5)。

半徑長度一定得到的條件,見式(6)。

利用初始水平面得到的條件,見式(7)、式(8)。

初始水位不同會導致粒子數不同,如表1、表2 所示。

表1 左上水箱水位不同情況下的粒子數

表2 右上水箱水位不同情況下的粒子數
長方體重心坐標,見式(9)。
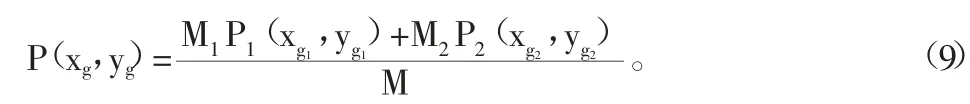
2 模型求解
通過對上下水箱的橫縱坐標改變量的整理可以得到左右各水箱的Δx,Δy 結果,并得到重心軌跡變化曲線。
這里以比例0.25 為例,如圖3 所示。
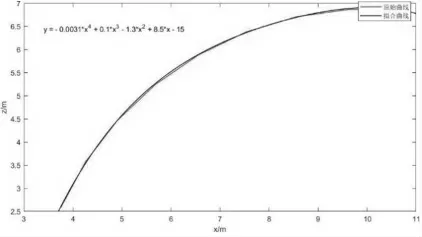
圖3 比例0.25 時重心的軌跡
3 形心軌跡模型
3.1 模型建立
形心軌跡如圖4 所示。
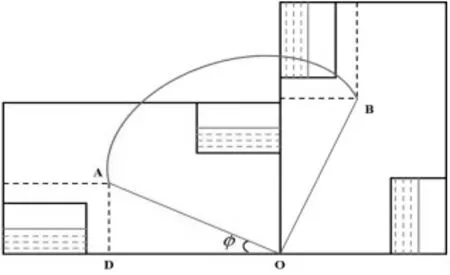
圖4 形心軌跡
根據形心相對位置不變條件得到半徑,見式(10)。

根據角度的條件得到式(11)。

3.2 模型的求解
根據兩點間距離見式(12)~式(14)。
d=-0.002046θ4+0.07112θ3-0.992θ2+6.172θ-11.91; (12)
d=-0.003081θ4+0.1028θ3-1.351θ2+8.509θ-1.51; (13)
d=-0.001418θ4+0.05115θ3-0.7564θ2+5.48θ-9.602。 (14)
重心與形心間隔隨φ 的變化如圖5~圖7 所示。根據圖像來看,在比例為0.25 時,兩心之間的距離都是隨著角度φ 的增大先減小后增大;在比例為0.5 時,兩心之間的距離都是隨著角度φ的增大先增大后減小;在比例為0.75 時,兩心之間的距離都是隨著角度φ 的增大持續減小。
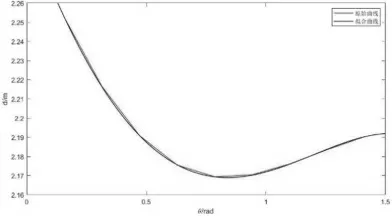
圖5 比例0.25 時重心與形心間隔隨φ 的變化

圖6 比例0.5 時重心與形心間隔隨φ 的變化
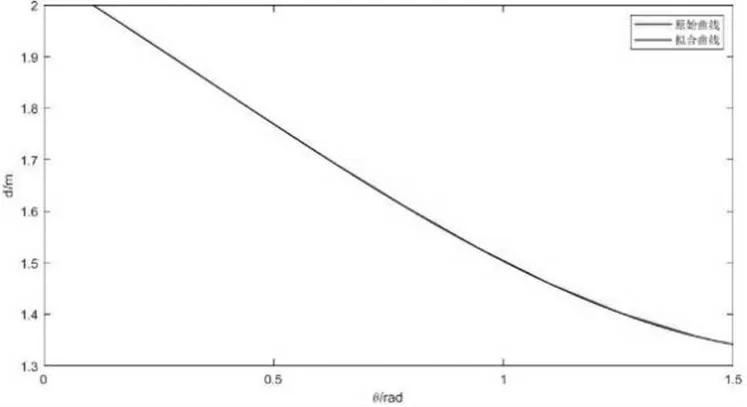
圖7 比例0.75 時重心與形心間隔隨φ 的變化
4 結論
本文圍繞實際生活中的水箱重心變化問題進行建模分析研究,基于SPH 粒子化思想和曲線擬合手段,將液體水看做若干等大等距的粒子來模擬了水流動過程。首先研究水箱中水比例相同時隨長方體反轉角度不同增大時該比例對重心與形心之間距離的影響,在求取距離同角度變化的函數時,以粒子的運動來代替流體的運動。最后對所有點進行求和操作,得到最終的重心運動軌跡。

