充填型巖溶管道致災機理研究

王青松

(1.中鐵二十局集團有限公司 陜西西安 710016；2.長安大學 陜西西安 710064；3.中國鐵建高原隧道施工技術及裝備研發中心 陜西西安 710016)

1 引言

突水突泥是巖溶隧道修建過程中最常見且極具危害性的一類災害，其往往具有突發性，極易造成重大經濟損失及人員傷亡[1－3]。巖溶隧道突水致災構造通常包括:斷層型、泥砂充填型溶洞、高壓富水溶洞、暗河、裂隙、填充型巖溶管道等類型[4－6]。其中充填型巖溶管道往往規模較小，前期地質勘察難以發現，在復雜的地下巖溶水循環路徑中，巖溶管道往往連接廣泛的地下水補給網路和充足的補給水源，隧道施工中一旦揭露，極易造成嚴重的工程災害和環境破壞。

當隧道開挖揭示填充型巖溶構造時，隧道是否發生突水與填充介質的性質和穩定性密切相關。由于填充介質的滲透性存在差異，其通常包括整體滑移和滲透失穩兩種破壞類型。當充填介質結構致密、膠結程度高，整體性好，其往往具有良好阻水能力，且與巖溶管壁結合緊密，起到了“瓶塞”的作用。填充型巖溶構造一旦揭示容易在隧道施工中持續的爆破振動以及巖溶靜水壓力的綜合作用下，填充物內部或巖溶管壁處發生剪切破壞，導致填充物大范圍滑動失穩而最終發生突水突泥[7－8]。當充填介質結構疏松、孔隙率大時，水流會對充填介質進行浸泡和沖刷，充填介質顆粒不斷被沖刷運移，管道內部的孔隙率越來越大，隨著較大介質顆粒散失，充填管道最終貫通導致隧道發生突涌水[9－10]。因此充填管道型巖溶通常表現為“延滯性潰水”。

對于充填管道型巖溶，很多學者做了相關研究。李術才(2015)[11]利用條分法計算了充填型巖溶蓄水構造突水突泥的安全層厚度。CHU Vietthuc(2016)[12]采用理論分析結合數值模擬，分析了充填型巖溶管道的突水機理及演化過程。儲漢東(2017)[13]利用極限平衡法建立充填體滑移失穩模型。黃震(2019)建立了充填型巖溶管道的力學傳遞模型，并推導出巖溶管道失穩判據及安全系數計算公式。本文針對充填體滑移失穩，忽略巖溶充填體的滲透水壓力，建立了巖溶管道充填體臨界安全厚度計算公式；針對充填體滲透失穩，建立了巖溶管道充填體滲透失穩力學模型；最后通過數值模擬揭示了充填型巖溶管道致災呈“滯后性”的內在機制，以期為相關工程實踐提供參考。

2 充填結構物滑移破壞

當充填介質結構致密、膠結程度高，整體性較好，滲透性較小時，具備優良的阻水能力，甚至可以將其視作隔水層，往往起到“瓶塞”作用。隧道開挖打破了原有平衡狀態，為充填體提供了整體滑動的致災條件，本文不考慮水的滲透力，建立充填體滑移失穩力學模型。

如圖1所示，將模型簡化為平面二維模型，溶管寬度為D，長度為L，溶管內為靜儲量巖溶水，水壓均布于充填體頂面；填充介質為完整致密體，僅在溶管壁處產生滑移而失穩；充填型溶管揭穿時失去原有支護力，即q＝0。

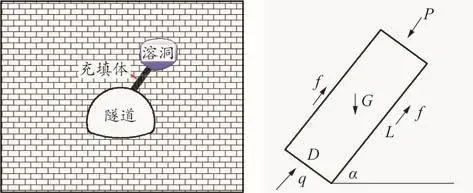
圖1 填充體滑移失穩力學模型

根據力的平衡，填充體的極限平衡方程為:

式中:F為充填體所受摩擦力；G、P和α分別為充填體所受重力、水壓力及充填體傾角，則有:

式中:γ為充填體容重；D和L分別為充填體寬度和長度；Pw為上部均布水壓。

充填體內部任一點的抗剪強度為:

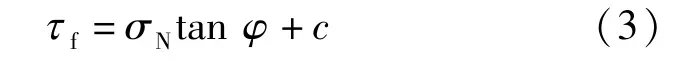
由于破裂面為直立面[13]，所以:

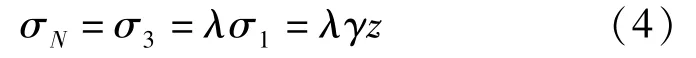
式中:λ為側壓力系數。

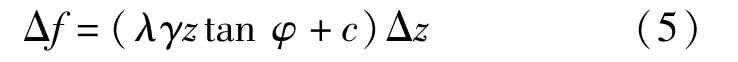
則該充填體側面受到摩擦力為:

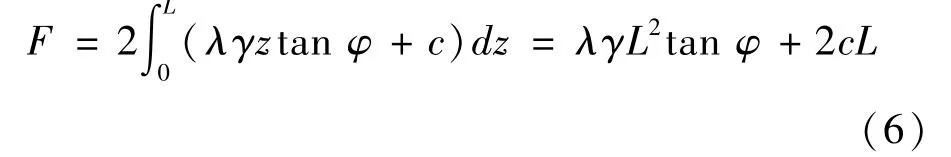
得到充填物滑移力學模型:

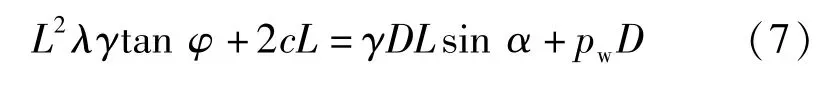
式(7)中等號左側為抗滑力，右側為致滑力。通過求解得到充填物滑移的臨界長度:

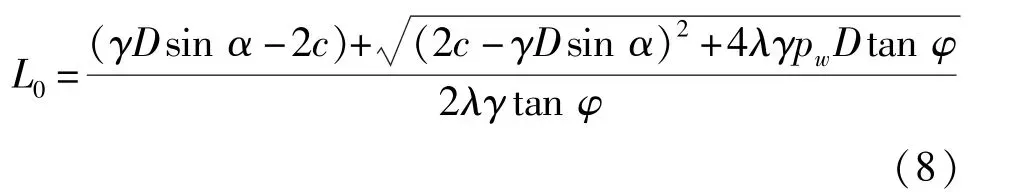
對充填滑移體臨界長度L0變化規律進行分析，假定充填體參數不變。

計算參數如表1所示，在研究滑移體臨界長度L0與寬度D的關系時，假定其他三項不變，并以此類推，得到滑移體臨界長度L0隨寬度、傾角、側壓力系數及水壓的變化規律，如圖2～圖5所示。

表1 滑移充填體計算參數

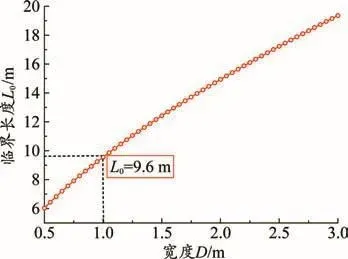
圖2 臨界長度隨管道寬度變化規律

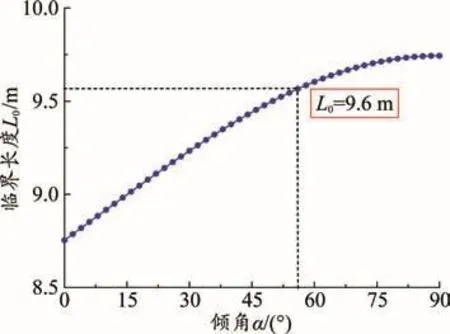
圖3 臨界長度隨管道傾角變化規律

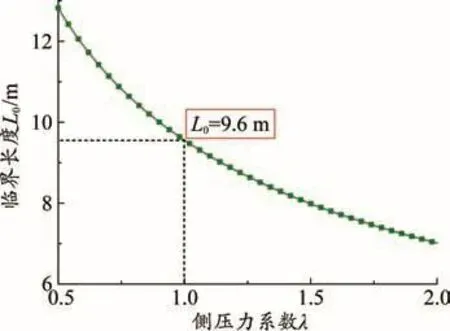
圖4 臨界長度隨側壓力系數變化規律

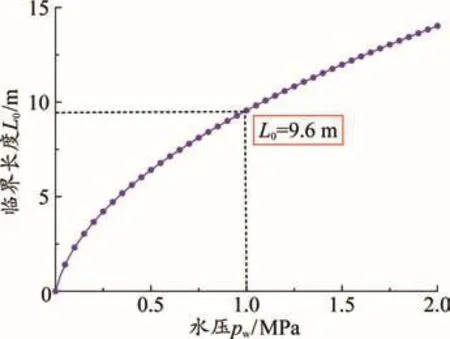
圖5 臨界長度隨水壓變化規律

(1)充填滑移體臨界長度L0隨寬度D的增加而增大，但增長速率呈現減小趨勢，當充填體寬度D在2.0 m以上時，臨界長度L0隨寬度D近似呈現線性增加關系。

(2)充填滑移體臨界長度L0隨傾角的增加而增大，增長速率呈現減小趨勢，當充填體傾角小于45°時，充填滑移體臨界長度隨傾角α增加近似呈線性增長；傾角大于60°時，增長率明顯降低；傾角在75°～90°，充填滑移體臨界長度幾乎保持不變。

(3)側壓力系數λ的增大意味著摩擦力的增大，因此充填滑移體臨界長度隨側壓力系數的增加而減小，但其減小的速率逐漸變小。例如側壓力系數從0.5增加到1.0時，臨界長度L0從12.8 m減小為9.6 m，降低了約25%；而側壓力系數λ從1.0增加到1.5時，臨界長度L0從9.6 m減小為8.0 m，只降低了約17%。

(4)充填滑移體臨界長度隨水壓的增加而增大，當水壓較小時增速較快，當水壓較大時增速逐漸降低。例如水壓pw從0.5 MPa增加到1.0 MPa時，臨界長度L0從6.4 m增大為9.6 m，增加了50%；水壓pw從1.0 MPa增加到1.5 MPa時，臨界長度L0從9.6 m增大為12.0 m，增加了25%。

值得注意的是，實際施工中爆破等振動作用會對充填介質起到一定擾動作用，而且水的滲流會產生一定的滲透力，為了簡化計算此處并沒有考慮這些因素，因此建議在計算所得的臨界安全長度L0的基礎上乘以一定的安全系數η，即L＝ηL0，安全系數η亦可根據實際工程進行分析。

3 充填結構物滲透破壞

以圓形巖溶管道為例，將膠結緊致的充填介質視為一個整體，巖溶水的滲透力為體積力，并與滲流方向一致，當填充介質出現微小移動時，構建如圖6所示力學模型[12]。

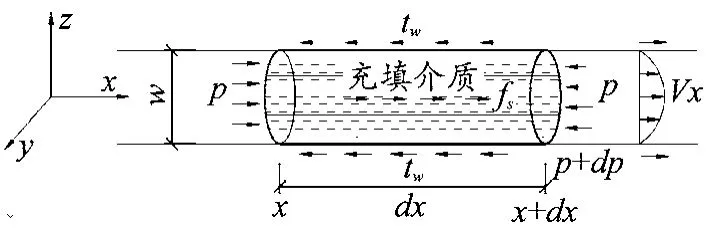
圖6 圓形填充型管道滲流示意

管道中任一點受到的水壓力為:

式中:為滲流產生的動水壓力矢量；γ為滲流水的容重；為水力坡度矢量。

設溶管沿x方向水力梯度變為J，則dx微元內的填充介質所受滲流力為:

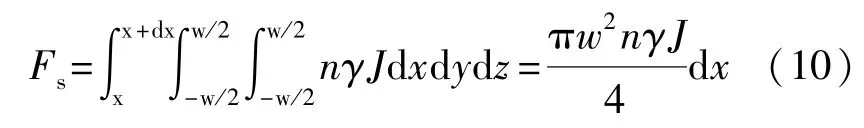
式中:J為水力坡度；n為填充介質孔隙率；w為圓形微管道直徑。

充填介質發生移動時，會受到管壁阻力，并且管壁阻力和充填介質對管壁的拖曳力互為作用力和反作用力，其大小為:

根據微元體的受力平衡有:

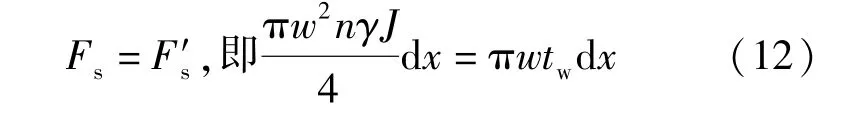
進一步得到:

當溶管內全為水體，沒有固體顆粒填充介質時，即n＝1，則:

式中:ρw為水的密度。

當固體填充介質顆粒發生移動時，將巖溶水和顆粒共同運動簡化為某種單相高密度流體，則其對管壁產生壓力:

式中:ρm為混合流體密度；ΔH為滲流總水頭和位置水體的水頭差。

此時，管壁受到流體的拖曳力為:

由于混合流體的密度ρm大于單一水體的密度，因此相對于巖溶水而言，泥砂混合流體對管壁的拖曳力更大，因此其擴徑作用也更為明顯。

4 巖溶管道突水演化過程分析

采用數值模擬對管道型巖溶突水過程進行模擬。計算模型尺寸為(160×160×2)m。假定巖溶管道上方連接高壓富水溶洞，水壓為1 MPa。隧道埋深100 m，圍巖孔隙率為0.2，滲透系數為1×10－10m/s；充填體孔隙率為0.3，滲透系數為1×10－8m/s，地層側壓力系數取1.0。數值模擬計算參數如表2所示，數值模擬計算結果如圖7所示。

表2 數值模擬計算參數

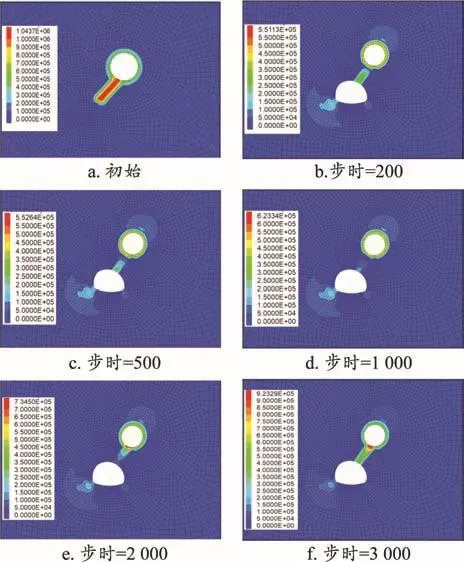
圖7 數值模擬滲流計算結果

由圖7可知，初始最大孔隙水壓力主要發生在巖溶管道的充填體處，隧道開挖以后充填體的孔隙水壓力呈現先減小再增大的變化規律，這是因為隧道開挖以后形成臨空面，加速了充填體內部孔隙水的流通；同時由于充填體結構致密，具有很好的阻水性，因此上部的巖溶水還未補充，隨著時間的增加，上部水體通過滲流作用再次補充了充填體內部的孔隙水，并且水壓持續增大，最終充填體發生滑移破壞，反映出管道型巖溶突水突泥呈現“延滯性”的特征。

5 結論

本文針對管道型巖溶致災機理進行研究，主要取得以下結論:

(1)建立了巖溶管道兩種失穩模型，包括充填滑移破壞和滲透失穩破壞，且推導了不考慮水體滲透力時充填滑移破壞類型的臨界安全厚度計算公式。

(2)管道型巖溶充填滑移體臨界長度隨寬度的增加而增大，但增長速率呈現減小趨勢；當充填體傾角小于45°時，充填滑移體臨界長度隨傾角近似線性增加，當傾角大于60°時，增長率明顯降低；充填滑移體臨界長度隨側壓力系數的增加而減小，但其減小的速率逐漸變小；臨界長度隨水壓的增加而增大，但增速逐漸降低。

(3)隧道開挖以后充填體的孔隙水壓力呈現先減小再增大的變化規律，并且隨著水壓持續增大，充填體最終發生滑移破壞，反映了管道型巖溶突水突泥呈現“延滯性”的特征。