地下綜合管廊地震響應及影響因素分析研究

吳東浩

(中鐵建設集團有限公司 北京 100040)

1 引言

城市地下綜合管廊作為城市的“生命線工程”，在電力、供暖、給排水等方面發揮著重要作用[1]。我國是個多震的國家，城市的抗震設防尤為重要，因此，綜合管廊的抗震設計也得到了越來越多的關注。

岳慶霞[2]利用ABAQUS軟件建立地下管廊的三維模型，研究了行波效應及邊界條件等影響因素對管廊縱向動力特性的影響規律；王鵬宇[3]、唐征武[4]通過分析指出地下管廊地震破壞時的薄弱環節在頂板、底板與側墻的連接部位以及中隔墻的墻端；施有志[5]利用PLAXIS軟件，建立綜合管廊有限元模型，比較了靜力作用和動力作用下接觸面參數對結構內力的影響，結果表明在相同接觸面折減系數條件下，底部地震波輸入產生的結構內力極值顯著高于僅有Rayleigh波輸入的情況；張博華[6]采用MIDAS有限元軟件，重點對處于高烈度地震區地下綜合管廊交叉口節點進行非線性動力時程分析，結果表明反復處于拉壓受力狀態下的交叉口節點與標準段連接處的角點是結構受力的薄弱部位，在具體結構設計時應予以重視；蔣錄珍[7]采用ABAQUS有限元軟件建立了飽和兩相土體中地下綜合管廊結構二維動力有限元模型，發現管廊結構的變形隨著埋深的增加和結構尺寸的增大而增大。

由此可見，地下綜合管廊的動力特性研究已經取得了豐富成果，但鑒于不同區域的土體性質差異較大，土體和結構非線性效應明顯且動力相互作用復雜，仍有必要進行地下管廊的動力研究。

2 地下綜合管廊的地震動力響應分析

北京新機場市政交通工程綜合管廊位于北京市大興區，管廊采用矩形三艙形式，埋深h＝3 m。當地土層主要為人工堆積粉土、有機質黏土、砂質粉土和重黏質粉土。

2.1 計算模型及參數

計算采用的模型為:土體尺寸為(40×20)m，管廊結構尺寸為(9.3×3.6)m，其中側墻及頂板、底板厚0.4 m，中隔墻厚0.25 m。

土體的本構模型采用Mohr-Coulomb理想彈塑性模型，各層土體材料參數見表1。

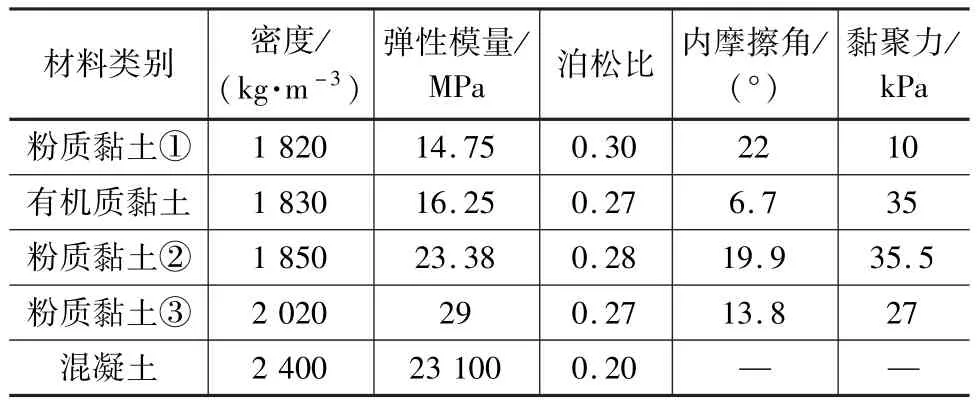
表1 土體和混凝土的材料參數

管廊結構混凝土強度為C30，材料參數見表1。混凝土采用混凝土塑性損傷模型(CDP)[8]，CDP模型的應力－非彈性應變關系及損傷因子－非彈性應變關系見表2。

表2 __混凝土塑性損傷模型參數

2.2 模型構建

采用面與面接觸模型模擬管廊結構與土體的相互作用，法向接觸為硬接觸，切向接觸使用罰函數法模擬。ABAQUS有限元軟件中的無限元來模擬邊界條件，以矩形三艙模型為研究對象建立有限元計算模型，如圖1所示。土體和結構采用CPE4R單元，土層的網格尺寸為(0.5×0.5)m，結構網格尺寸為(0.2×0.2)m，如圖2所示。其中，選取內角點A1、A5、A7，側墻中點A2、A4、A6以及中隔墻端點A3共7個點作為計算不同影響因素下地震響應的輸出點，如圖1所示。

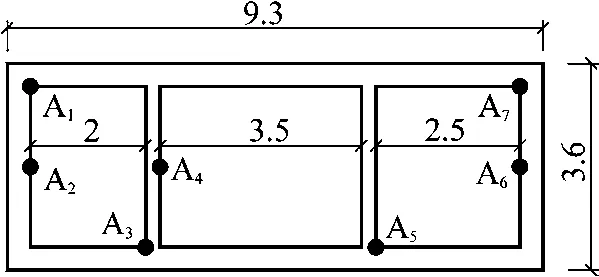
圖1 地下管廊矩形三艙模型(單位:m)

圖2 土體與地下管廊有限元模型

選擇El-Centro地震波作為入射波，其加速度時程曲線如圖3所示。

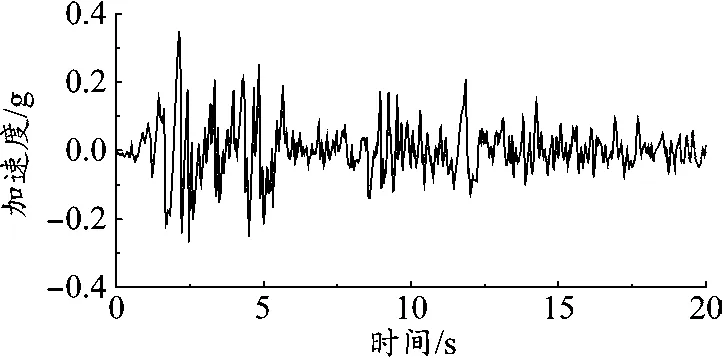
圖3 El-Centro波加速度時程曲線

3 地下管廊自振頻率及瑞利阻尼的確定

對于一般地下結構，其振動形式主要取決于圍巖介質，但對于淺埋結構的地下管廊與其他地下結構有一定程度上的差別，有必要對此進行說明[9]。本文利用ABAQUS軟件，分別建立土體－地下管廊結構模型和此模型相同尺寸的單純的土體模型，列于表3。

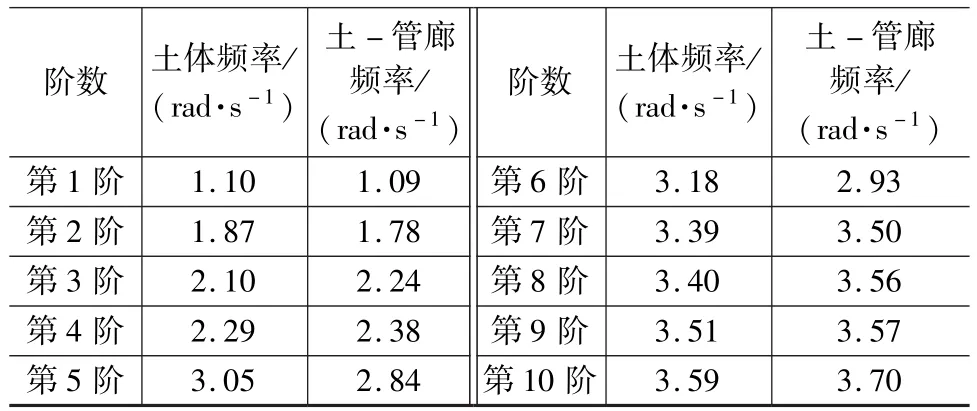
表3 土體與土－管廊自振頻率對比

從表3中可以發現在5階以下時，兩者的自振頻率相差較小，而高于5階后土－管廊的頻率明顯比土體的頻率要大，這說明此時的地下管廊對整體自振頻率的貢獻開始變的越來越大，但為了避免瑞利阻尼導致計算結果失真，通常選取前3階自振頻率，因此對于地下管廊的自振頻率計算可以直接使用土體的自振頻率。本文假定阻尼比ξ1＝ξ2＝0.05，選取表3第1階和第2階頻率，可以計算得到阻尼比例系數α＝0.072 3和β＝0.032 8。

4 地震響應影響因素分析

地下綜合管廊的地震響應影響因素有很多，本文重點考慮管廊形狀、管廊結構埋深、地震波峰值加速度、地震波的耦合對管廊應變及應力響應的影響規律。

以矩形三艙模型為基礎，采用與此凈空斷面面積相等的原則，分別建立矩形兩艙模型、矩形兩層四艙模型及L形三艙模型。為了對比管廊形狀的地震響應影響規律，分別選取結構的內角點A1、側壁中點A2、內壁端點A3、內壁中點A4共4個點進行分析，如圖4所示。

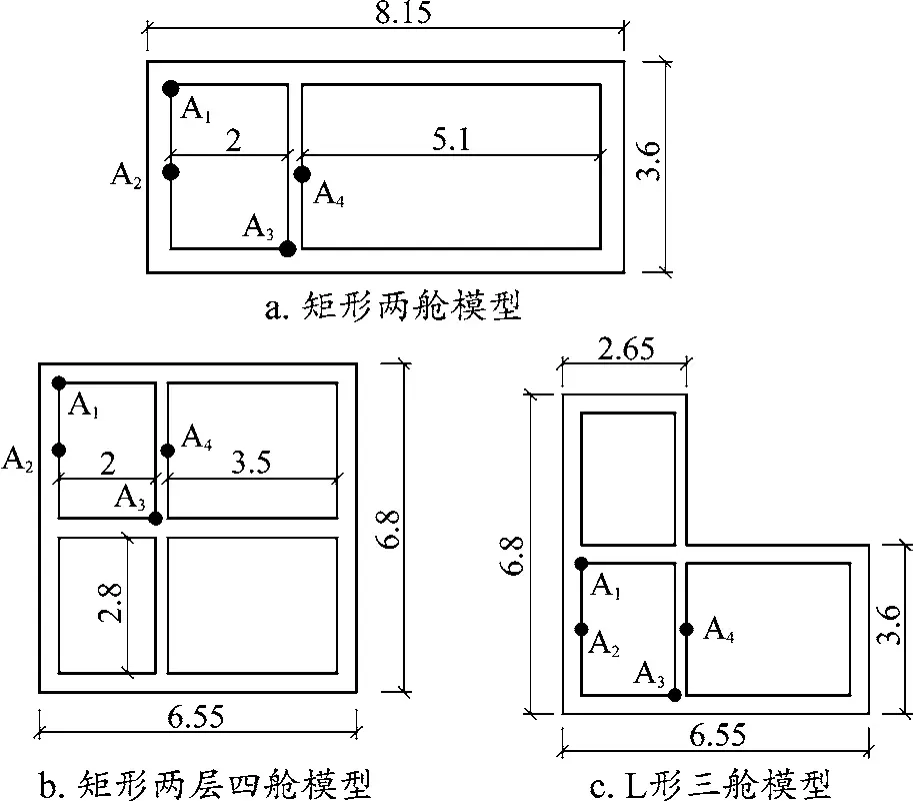
圖4 不同形狀的管廊尺寸及計算輸出點(單位:m)

在覆土深度h＝3 m的基礎上，考慮3種埋深，分別為0、0.5h和2h。考慮到各地區抗震設防烈度不同，將地震波峰值加速度分別調整為0.1g(7度)、0.2g(8度)、0.4g(9度)；在地震波的耦合研究中，分別考慮縱波、橫波以及縱波與橫波耦合對計算結果的影響。

4.1 管廊形狀的影響

由于管廊形狀的改變，其受力情況也會發生變化[10]。本文主要比較在水平地震波峰值加速度amax＝0.2g、管廊埋深h＝3 m的情況下，矩形三艙斷面、矩形兩艙斷面、矩形兩層四艙斷面、L形三艙斷面的輸出點水平應變峰值εx，max與豎直應變峰值εy，max，從而判斷管廊形狀對地震響應的影響。

表4與表5列出了輸出點A1、A2、A3和A4的水平與豎直應變峰值。從表中可以看出，對于頂板、底板與側墻的連接部位而言，矩形兩艙、矩形三艙形狀的管廊水平與豎直應變均較小，這說明地震響應較小；而對于矩形兩層四艙形狀和L形三艙形狀的管廊，由于與土體接觸面積較大，應變也相對較大，即規則的結構地震響應較小，而不規則的結構能增強其功能性，但也會使結構偏向不安全。故采用矩形兩艙斷面或矩形三艙斷面更適合減弱地震作用對管廊的破壞。

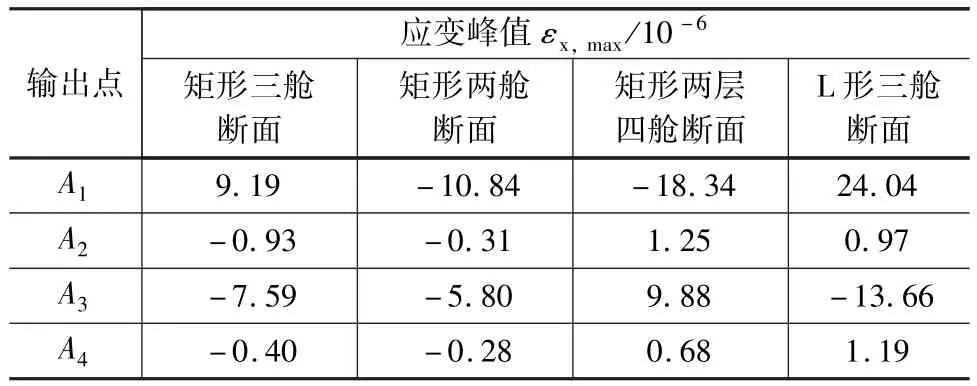
表4 不同斷面各輸出點水平應變峰值

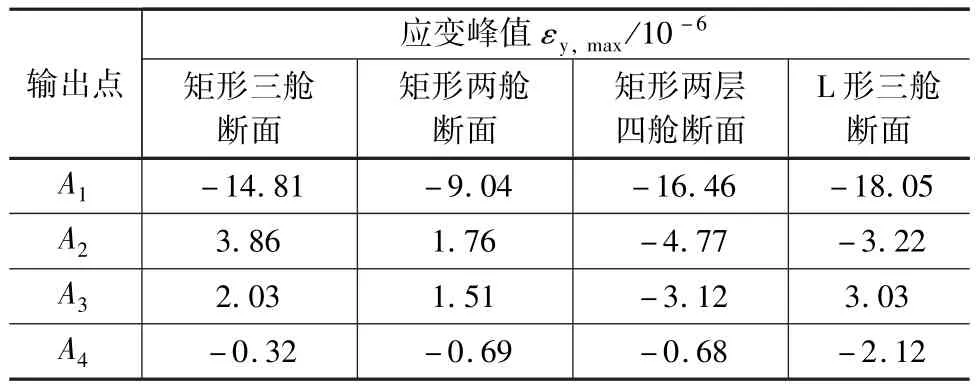
表5 不同斷面各輸出點豎直應變峰值

4.2 管廊埋深的影響

在管廊建設線路中，會出現管廊埋深的變化，隨著管廊埋深改變，與其所接觸土層的性質也會發生變化。本文主要比較在水平地震波峰值加速度為0.2g，管廊埋深分別為0、0.5h、h和2h的情況下，計算輸出點A1、A2、A3、A4、A5、A6和A7的水平應變峰值εx，max與豎直應變峰值εy，max。

由表6和表7可知，除了A2點外，其余各點的水平應變峰值隨著結構埋深增大而增大，這說明管廊的地震響應也越大。此外，結構的角點A1與A7應變值較其他點明顯要大，這說明應該重點關注角點的抗震設計。

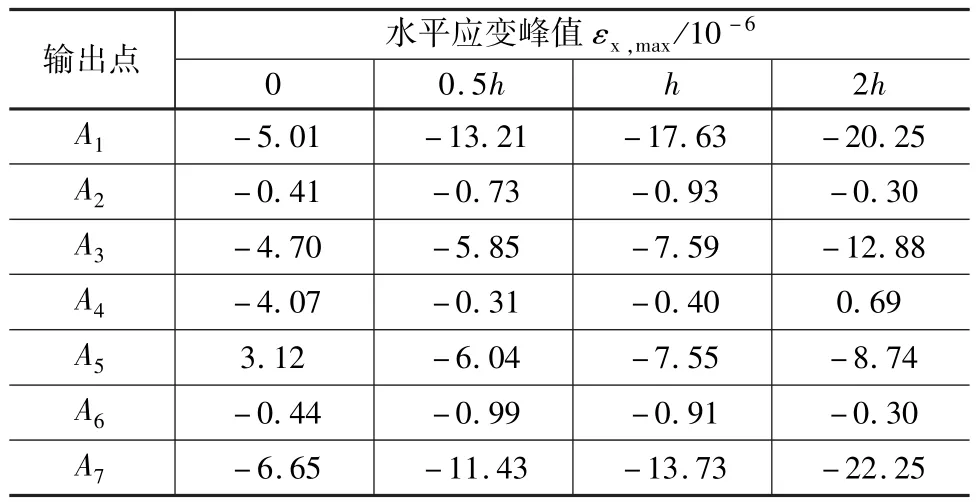
表6 不同埋深各輸出點水平應變峰值

4.3 地震波峰值加速度的影響

表8與表9為在不同峰值加速度的水平地震波作用下輸出點A1、A2、A3、A4、A5、A6和A7水平應力峰值σx，max與豎直應力峰值σy，max。

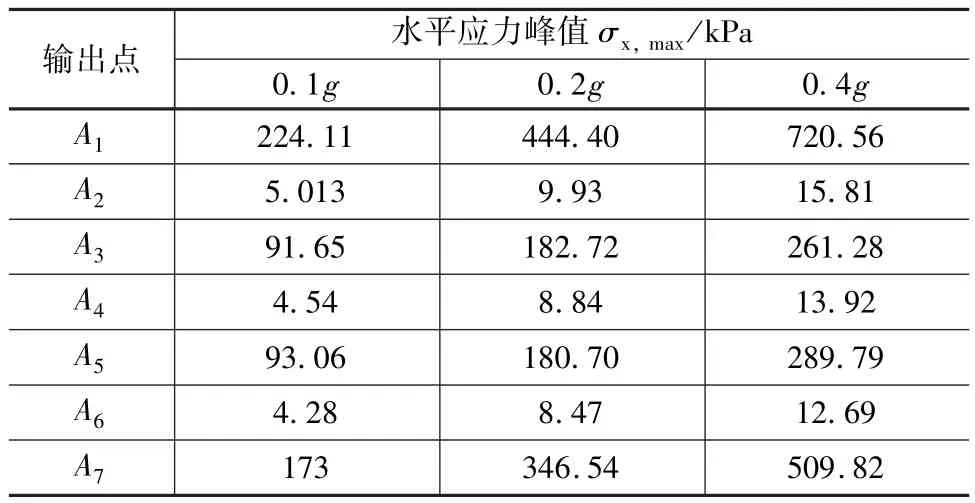
表8 各輸出點水平應力峰值

由表8和9可以看出，各輸出點應力峰值隨著地震波峰值加速度的增加而增大，這主要是由于地震波的峰值加速度越大，代表地震所包含的能量越大，結構的地震響應也就越大，對管廊造成的破壞程度自然也就越大，因此，進行管廊的結構設計時，要著重考慮其抗震等級。

4.4 地震波耦合的影響

管廊結構在受地震作用時，不但受橫波的影響，也會受縱波的影響。本文分別研究在橫波、縱波以及兩者耦合作用下結構的地震響應。其中，縱波與橫波的耦合系數取65%[11]，在地震波加速度峰值為0.2g的情況下，測定A1點的水平應力時程曲線。

圖5為橫波、縱波以及橫波與縱波耦合作用下，結構的水平應力時程曲線。綜合對比圖5可以發現，當地震波峰值加速度相同時，橫波與縱波耦合作用下，結構大部分時間段的應力都明顯比縱波與橫波結果要大；但水平地震波作用時結構應力峰值最大、耦合其次、縱波最小。這說明當地震波峰值加速度相同時，相比于橫波及橫波與縱波耦合作用，管廊結構在水平地震波作用下更容易被破壞。

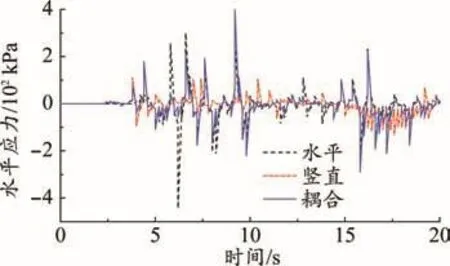
圖5 橫波、縱波及耦合作用下結構應力對比(A1點)

5 結論

以北京新機場綜合管廊工程為原型，采用ABAQUS有限元軟件建立二維有限元模型，研究各種因素對管廊結構地震響應的影響規律，得到了以下研究結論:

(1)對于地震波而言，其峰值加速度越大，地震波的能量也越大，管廊的地震響應也越大，故應根據各地的抗震設防烈度，合理提高管廊結構的抗震強度。

(2)管廊結構受地震波影響時，管廊結構在水平地震波作用下要比橫波及橫波與縱波耦合作用時更容易遭到破壞。

(3)管廊埋深對其地震響應有較大影響，埋深越大，管廊的應變也越大，故在建造管廊時，應考慮埋深的影響。

(4)不同形狀的管廊結構也會導致其不同的地震響應，在進行管廊設計時建議采用矩形兩艙或矩形三艙形狀的管廊。