具有標準發生率和Markov切換機制的隨機多群組SIR傳染病模型*

陳樺劍，韋煜明

（廣西師范大學數學與統計學院，廣西 桂林 541006）

0 引言

數學模型是描述傳染病的重要工具。許多數學模型提供研究傳染病傳播的根本機制，并提出傳染病的控制策略。[1]值得注意的是，Measles、Mumps、Gonorrhea和HIV/AIDS等傳染病是在異質人群中傳播的。為了描述上述疾病在異質人群中的傳播，學者們提出多群組傳染病模型。[2]一個異質人群可以通過傳播方式、接觸模式、地理分布劃分為幾個同質群組，使得群組內部和群組之間的相互作用可以分別建立模型。最早的多群組傳染病模型之一是由Lajmanovich和Yorke根據Gonorrhea的傳播提出的。[3]從那時起多群組傳染病模型的成果逐漸呈現在世人面前。[4–8]

實際上，自然界中存在多種噪聲，如白噪聲和電報噪聲。確定性傳染病模型無法準確描述這些噪聲對傳染病傳播的影響。因此，傳染病模型中的參數并不是確定的常數，而是隨著環境中的連續擾動而圍繞著某些均值擾動。為了更好地揭示環境白噪聲的影響，學者們將參數擾動引入傳染病模型中，[9–12]例如Cao等人對兩群組的SIRS傳染病模型中的疾病傳播率βkk進行擾動，[13]得到了模型（1）:

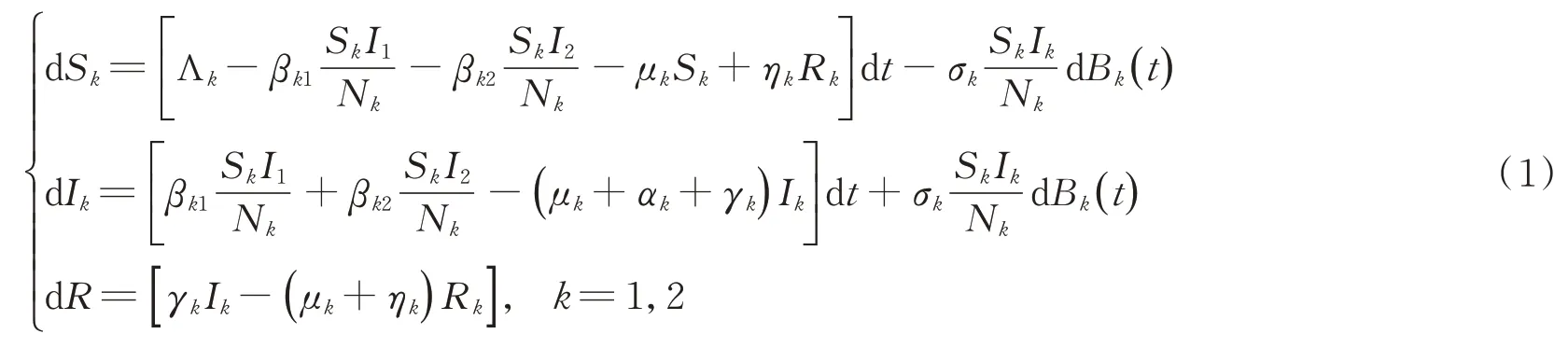
模型（1）各參數含義如下：Λk是表示在第k(k=1,2)個群組的人口輸入常率，βkj表示Sk和Ij(j=1,2)間的有效接觸率，μk表示在第k個群組中S、I、R各倉室中的自然死亡率，γk為第k個群組中染病個體的恢復率，ηk為第k個群組中免疫者失去免疫后重新變為易感者的比率，αk則表示第k個群組中染病個體的因病死亡率。假設參數γk、ηk和αk是非負的,而Λk、μk和βkj是正的，特別地,Bk表示相互獨立的標準布朗運動,σk是白噪聲強度，k,j=1,2。

除了白噪聲之外，電報噪聲對傳染病模型也有影響。例如，傳染病模型中的有效接觸率βkj在不同的季節影響下有很大的不同。學者們通常使用有限狀態空間中連續時間的Markov鏈模擬環境狀態的隨機切換。[14–17]連續時間Markov鏈通過Markov狀態切換得到傳染病模型中主要參數的變化。對于人類而言，研究疾病的有效傳播率βkj受到環境波動影響比研究其他參數更有意義。因此，Liu和Jiang提出了一個帶標準發生率和Markov切換的多群組隨機SIS傳染病模型，只對倉室Sk和Ij間的疾病有效傳播率βkj進行擾動：[18]

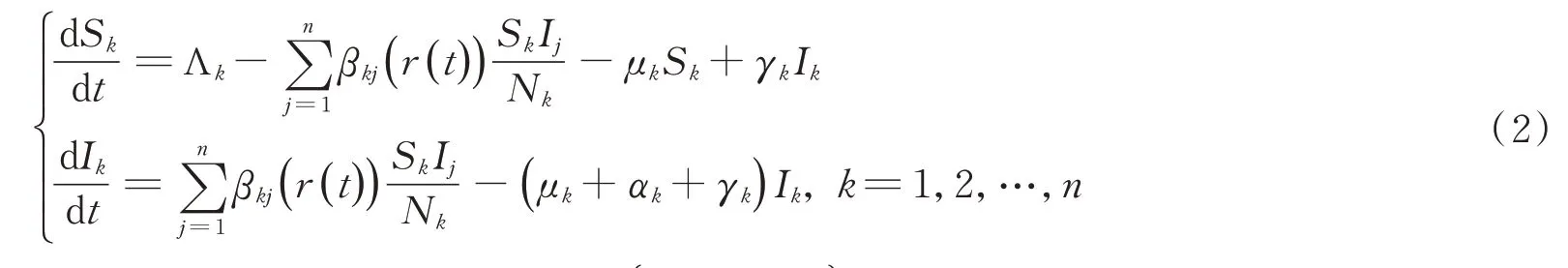
其中，有效傳播率βkj是一個同質連續時間Markov鏈{r(t),t≥0}在一個代表不同環境的有限狀態空間S={1,2,…,N}中取得的，Markov鏈{r(t),t≥0}是由轉移速率矩陣Γ=(δij)N×N產生的。

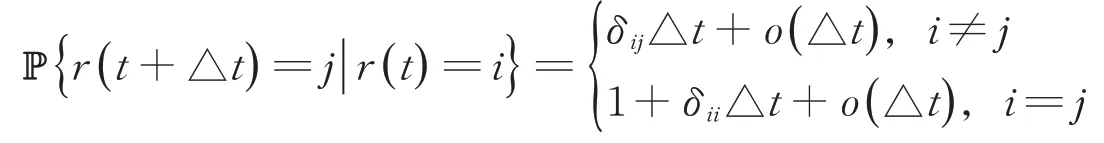
其中，△t>0表示一個小的時間間隔，δij表示從狀態i切換到狀態j的轉移速率，δij≥0，當i≠j時，有成立。對?l∈S，βkj(l)均為正常數。

受到模型（1）和模型（2）的啟發，筆者提出一項具有標準發生率和Markov切換機制的隨機多群組SIR傳染病模型：

模型（3）中各參數的意義與模型（1）和模型（2）保持一致。沿用Liu和Jiang的設定，本文假設Markov鏈是不可約的，也就意味著系統可以從一個機制切換到另一個機制。[18]對于?i,j∈S，存在有限數i1,i2,…,il∈S使得δi,i1,δi1,i2,…,δil,j>0，根據有限狀態的馬爾科夫理論，可以推斷其擁有遍歷性質。注意到Γ總是擁有一個平凡特征值，由于Markov鏈是不可約的，因此rank(Γ)=N-1。在上述條件下，Markov鏈擁有唯一一個平穩概率分布π=(π1,π2,…,πN)∈R1×N。此外，這個平穩分布可通過求πΓ=0確定，服從于且πi>0,?i∈S。

定義Rd+={x=(x1,x2,…,xd)∈Rd:xi>0,1≤i≤d}。令表示一個帶參考族{Ft}t≥0的完備概率空間，并且滿足一般條件：{Ft}t≥0單調遞增右連續，且F0包含所有零測集。對任意的常數列{g(i):i∈S}，定義。系統（3）前兩個方程均與R無關，為了方便，下文僅對模型（4）進行討論。

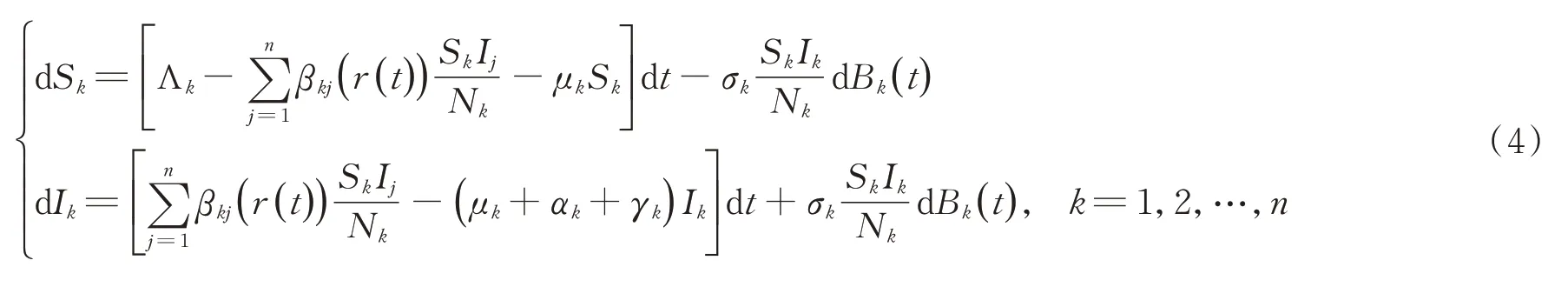
1 全局正解的存在唯一性

本節證明模型（4）全局正解的存在性。

定理1對于任意初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈×S，系統（4）存在一個唯一正解(S1(t),I1(t),…,Sn(t),In(t),r(t))，此正解以概率1保持在×S中，換言之，即

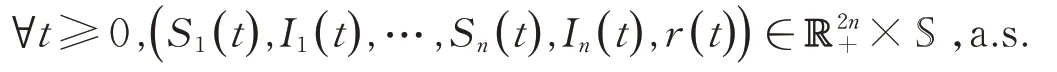
證明：由系統（4）可知，系統（4）中的系數滿足局部的Lipschitz條件，對于給定的初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈×S，系統（4）存在一個局部解(S1(t),I1(t),…,Sn(t),In(t),r(t))，?t∈[-τ,τe]，其中τe是爆破時間。

只有證τe=+∞，a.s.，才能說明解(S1(t),I1(t),…,Sn(t),In(t),r(t))是全局的。

令m0≥0充分大，使得Sk(0)，Ik(0)(k=1,2,…,n)均在區間中。對任意整數m≥m0，定義一個停時：

τm=inf{t∈[0，τe)：min{Sk(t)，Ik(t)，k=1，2，…，n}≤或max{Sk(t)，Ik(t)，k=1，2，…，n}≥m}

本文定義inf?=∞（?表示空集）。根據停時的定義可知，當m→∞，τm是單調遞增的，記，因此τ∞≤τe，a.s.若τ∞=+∞，a.s.，則τe=+∞，a.s.，說明解(S1(t),I1(t),…,Sn(t),In(t),r(t))是全局的。

下面利用反證法證明。假設τ∞<+∞，則存在兩個正常數T和ε∈(0,1)，使得P{τ∞≤T}>ε。因此，存在m1≤m0，使得P{τm≤T}>ε，?m≤m1。

一方面，?t≤tm，對于任意k(k=1,2,…,n)均有

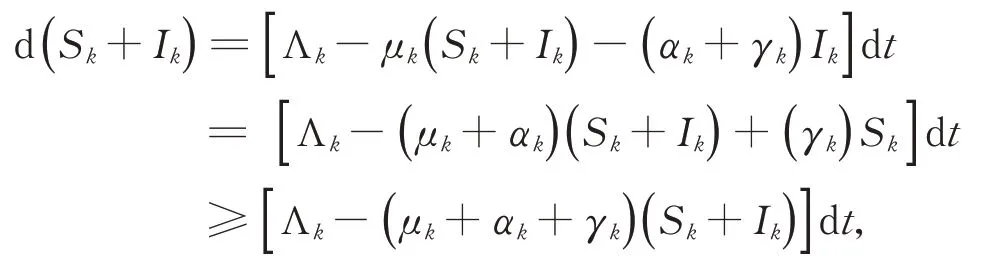
可得

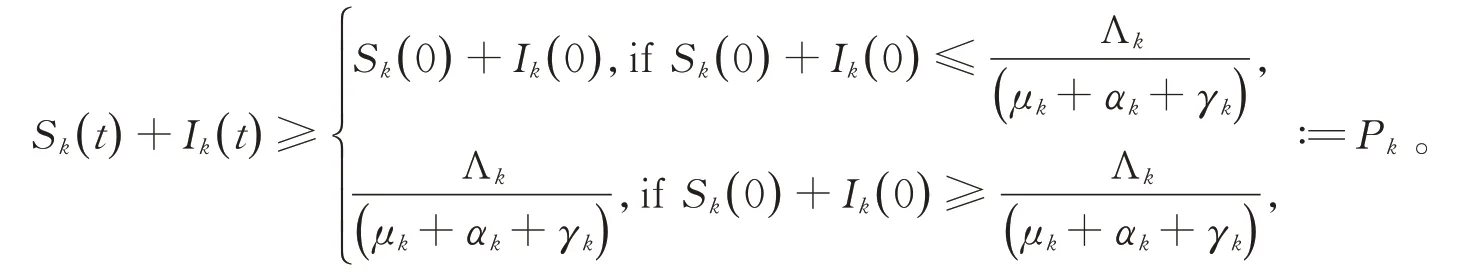
另一方面，?t≤tm，對于任意k(k=1,2,…,n)均有

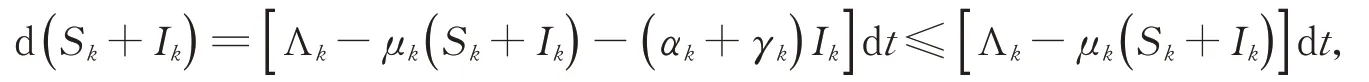
可得

定義一個C2函數，

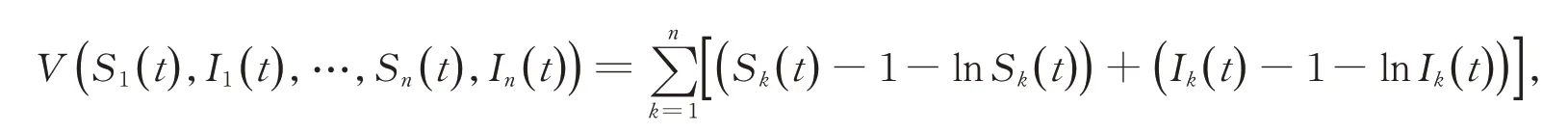
顯然，函數u-1-lnu≥0,?u>0是非負的，對C2函數V應用Ito?公式，可獲得

其中，

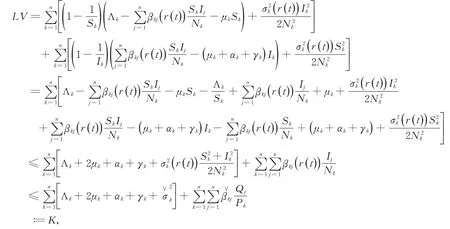
K是一個正常數。余下的證明與Dalal等證明類似，[19]故在此忽略。

由此可以證得：系統（4）存在一個唯一正解(S1(t),I1(t),…,Sn(t),In(t),r(t))，此正解以概率1保持在×S中。

注意1:對任意初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈×S，模型（4）存在一個唯一正解(S1(t),I1(t),…,Sn(t),In(t),r(t))∈×S，因此

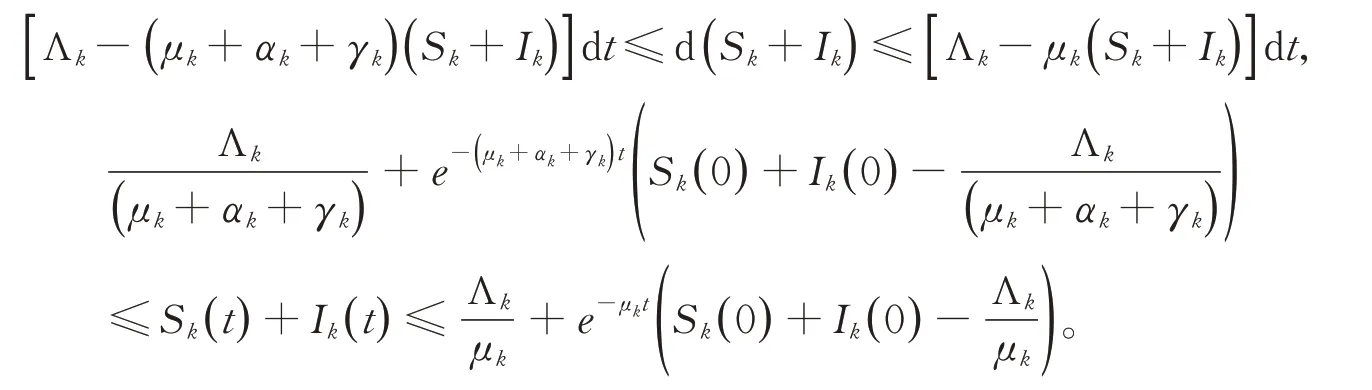
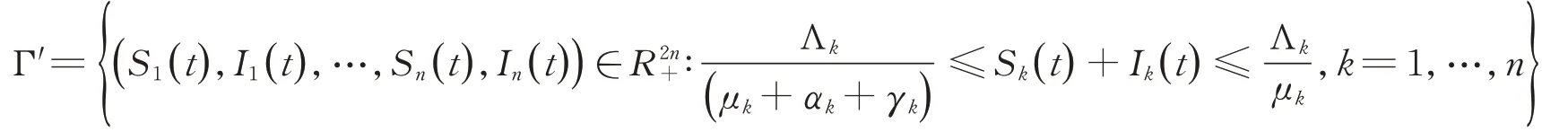
是系統（4）的一個正不變集。

2 傳染病的滅絕與持久

本節討論具有標準發生率和Markov切換機制的隨機多群組SIR傳染病模型（4）滅絕與持久的充分條件。

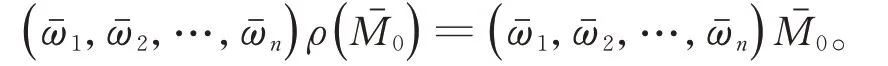
2.1 傳染病的滅絕

定理2假設是不可約的，令(S1(t),I1(t),…,Sn(t),In(t),r(t))∈×S是傳染病模型（4）帶初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈Γ′×S的一個解。如果下列任意一個條件成立：

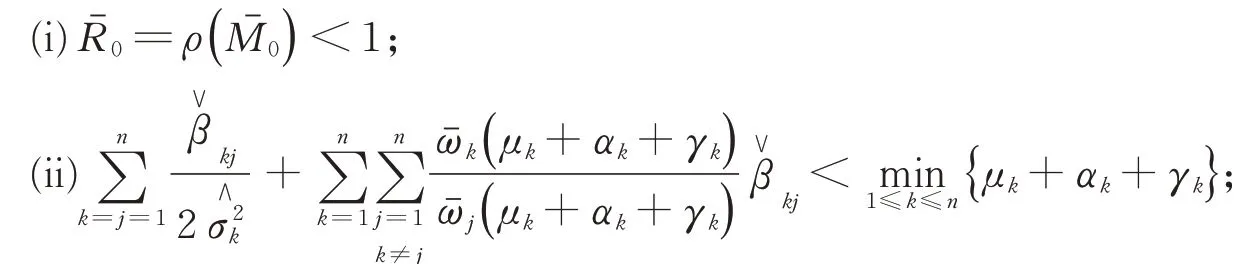
則傳染病Ik(k=1,2,…,n)依概率以1滅絕，即=0,a.s.,k=1,2,…,n。

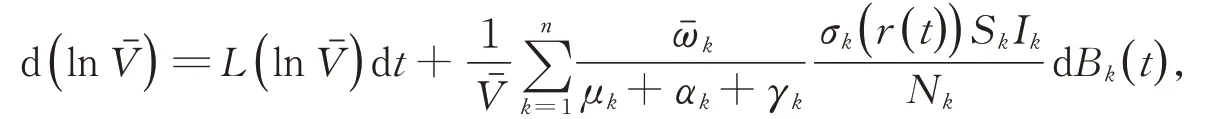
其中，

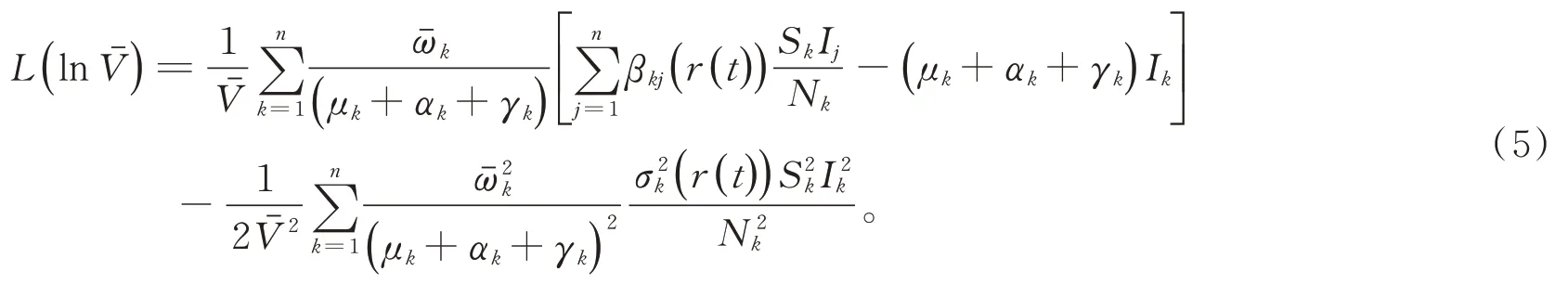
情況1：當條件（i）成立,有

因而,

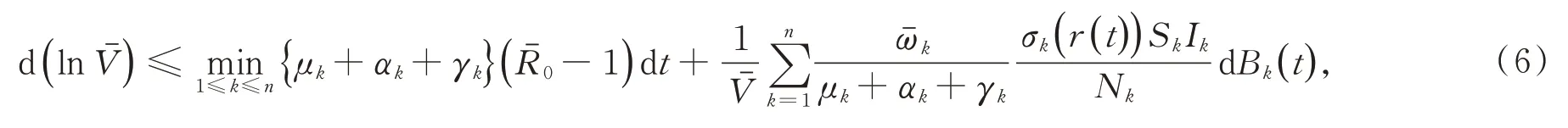
對（6）兩邊從0到t積分，并除以t

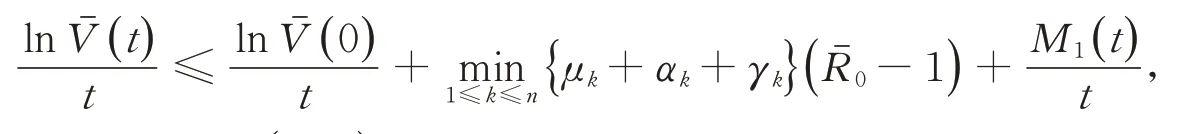
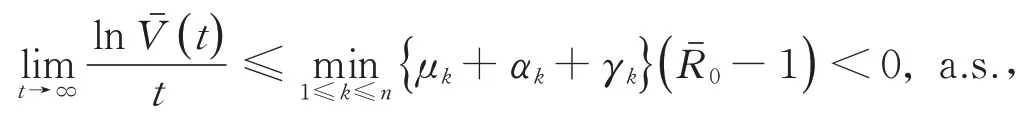
因此,

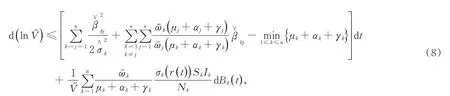
對（8）兩邊從0到t積分，并除以t，得到

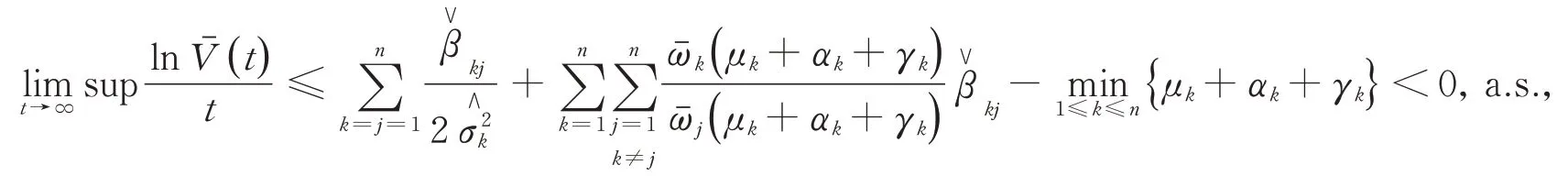
2.2 傳染病的持久

本小節給出傳染病持久的充分條件。

定義假設存在一個正常數c，如果>c>0,a.s.,(k=1,2,…,n)，則稱x(t)持久。

定理3假設是不可約的,(S1(t),I1(t),…,Sn(t),In(t),r(t))∈×S是傳染病模型（4）帶初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈Γ′×S的 一 個解。當，且時，傳染病Ik(k=1,2,…,n)將持久存在。

證明：定義一個函數V1(I1,I2,…,In)=，運用Ito?公式，得到

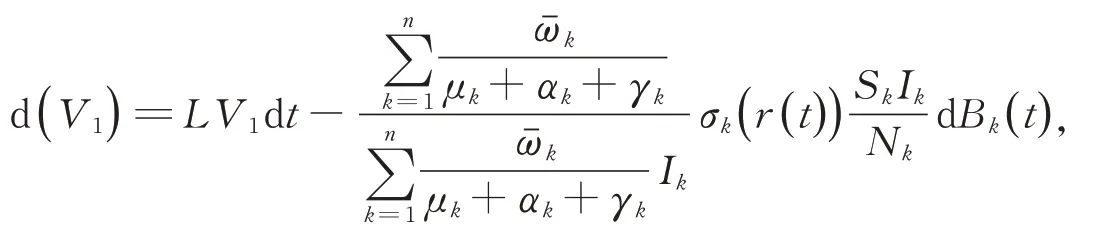
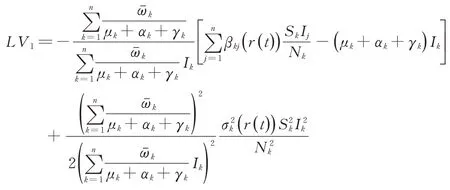
其中，

另一方面，定義V2(I1)=-I1，得到

其中

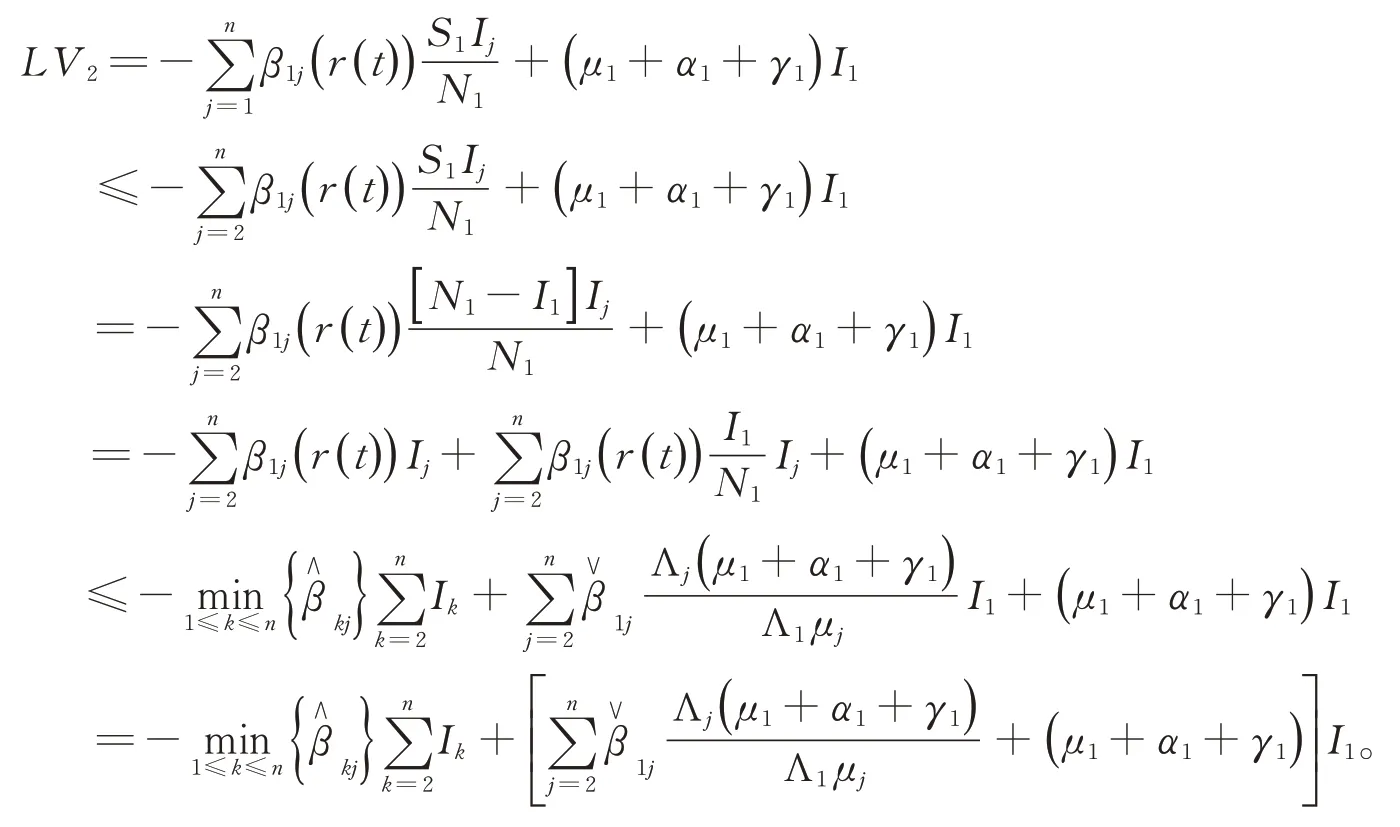
綜合考慮，定義

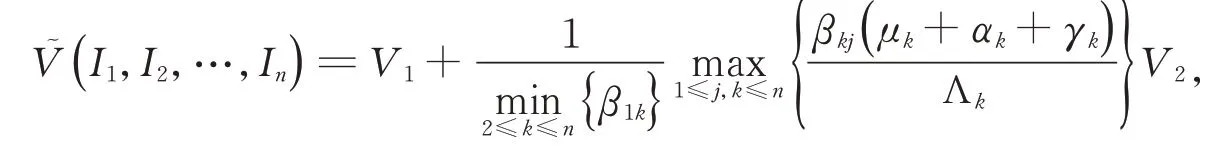
從而

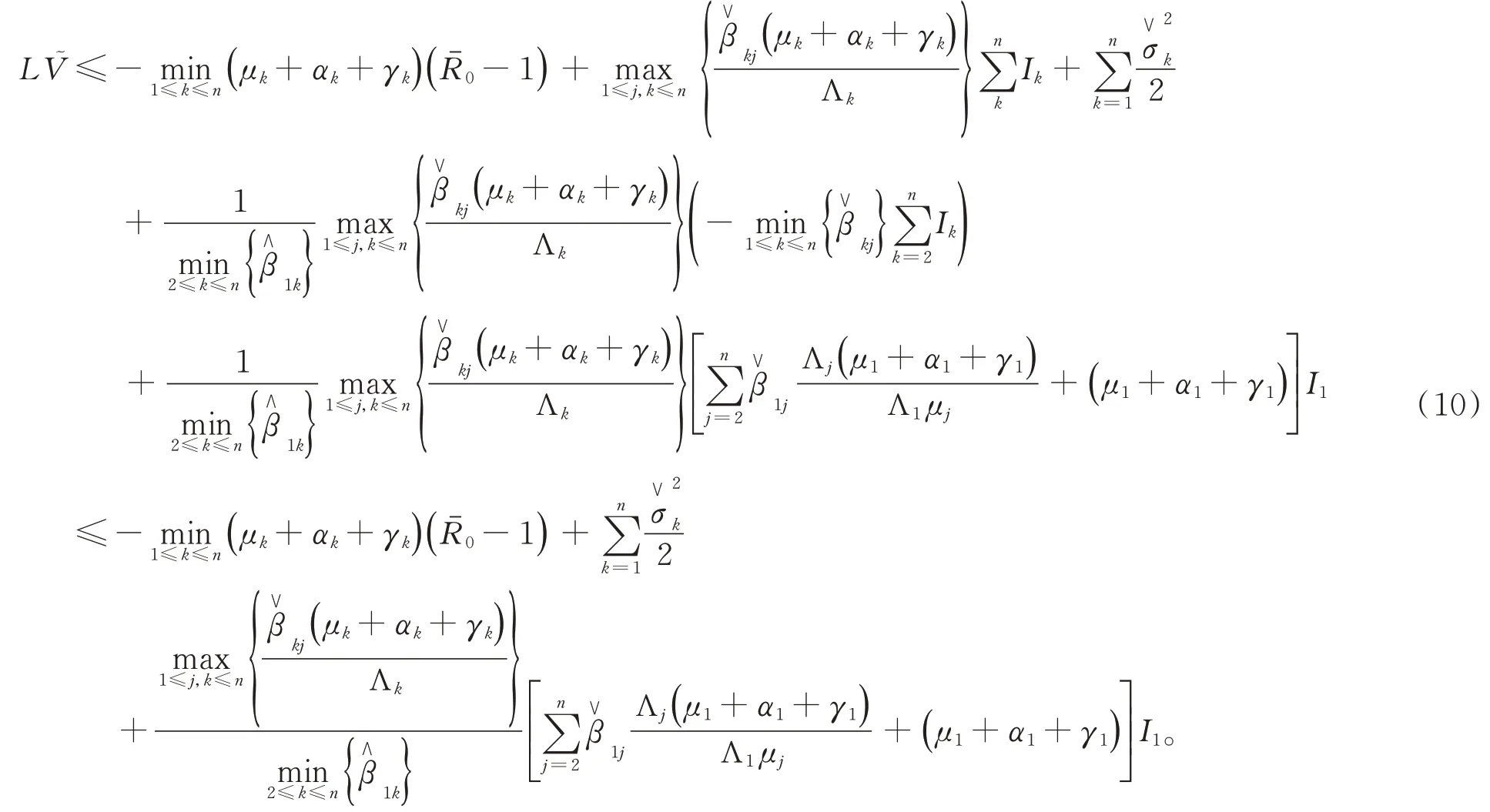
結合強大數定律，將（10）式從0到t積分，并除以t，得到

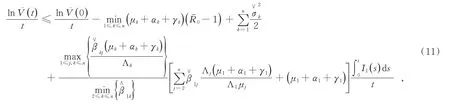
對（11）式進行變換，有

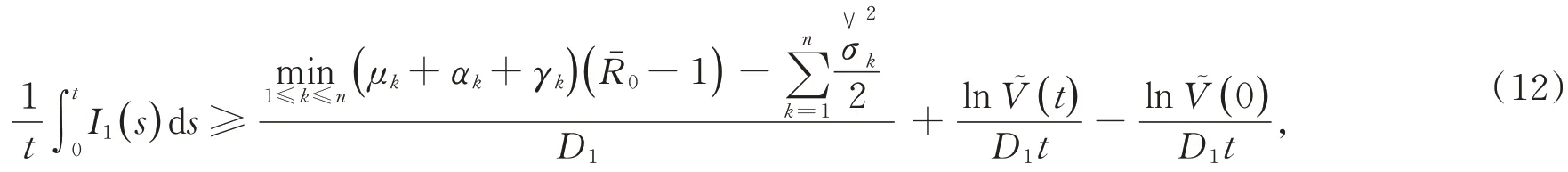
其中

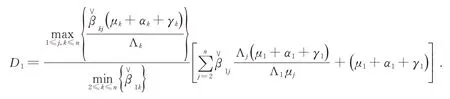
取（12）式下極限,可以得到

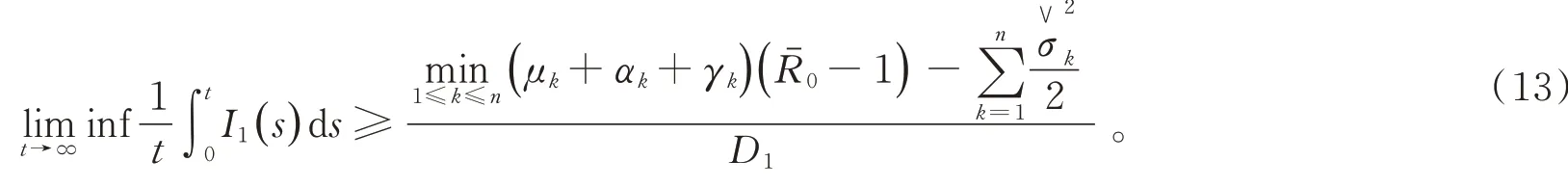
當定理3中的條件成立時，有

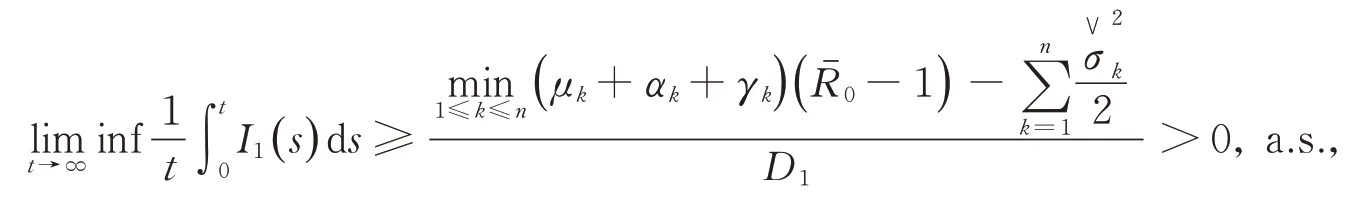
由此，我們可以推斷疾病I1將滅絕。

類似地，我們也可以得到

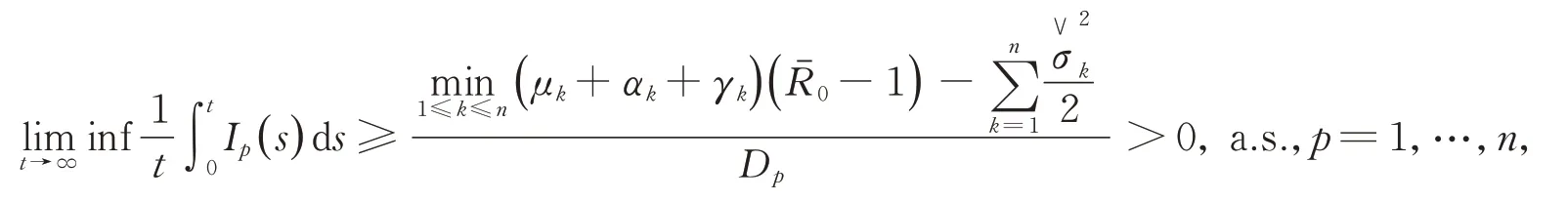
其中

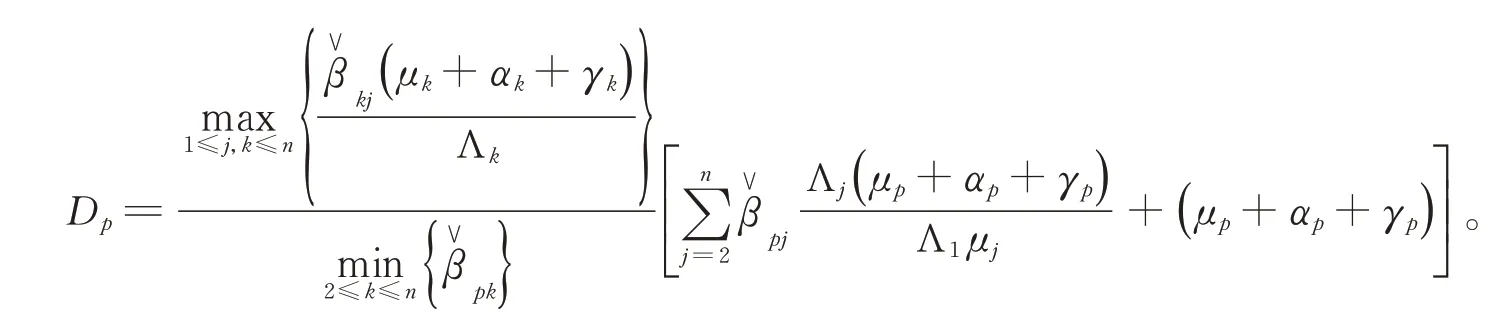
因此，傳染病Ik(k=1,2,…,n)將持久存在，定理3得證。

3 模型實例

在本節中提供兩個例子證實上述證明結果。為了簡便，此時取S={1,2}，k,j=1,2，討論兩個群組之間的傳染病傳播情況。

例1參考文獻[21]有如下取值:

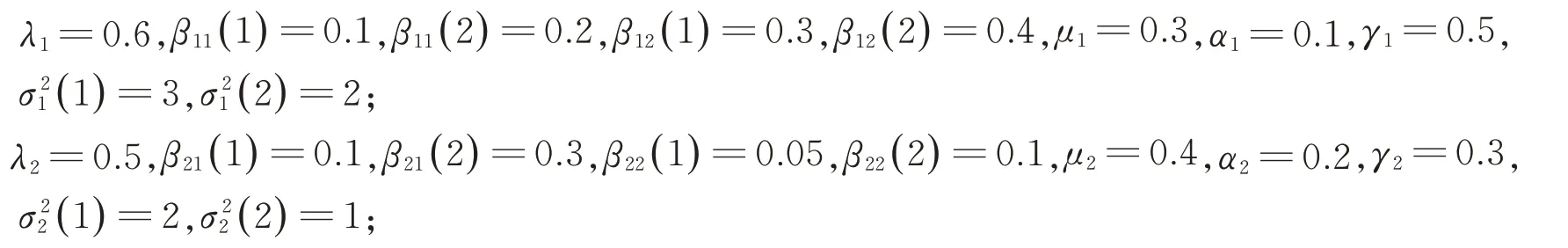
Case 1.

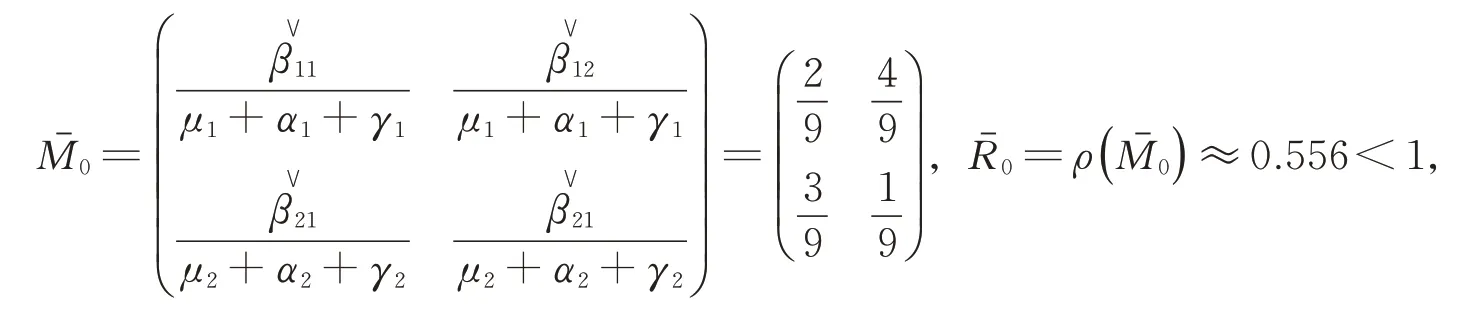
滿足定理2中的條件（i）,此時傳染病依概率以1滅絕。

Case 2.

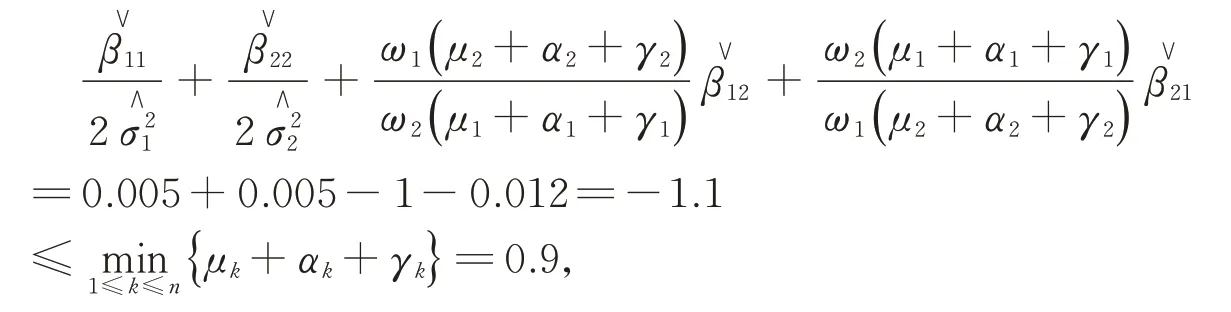
滿足定理2中的條件（ii），此時傳染病依概率以1滅絕。

例2取值如下:

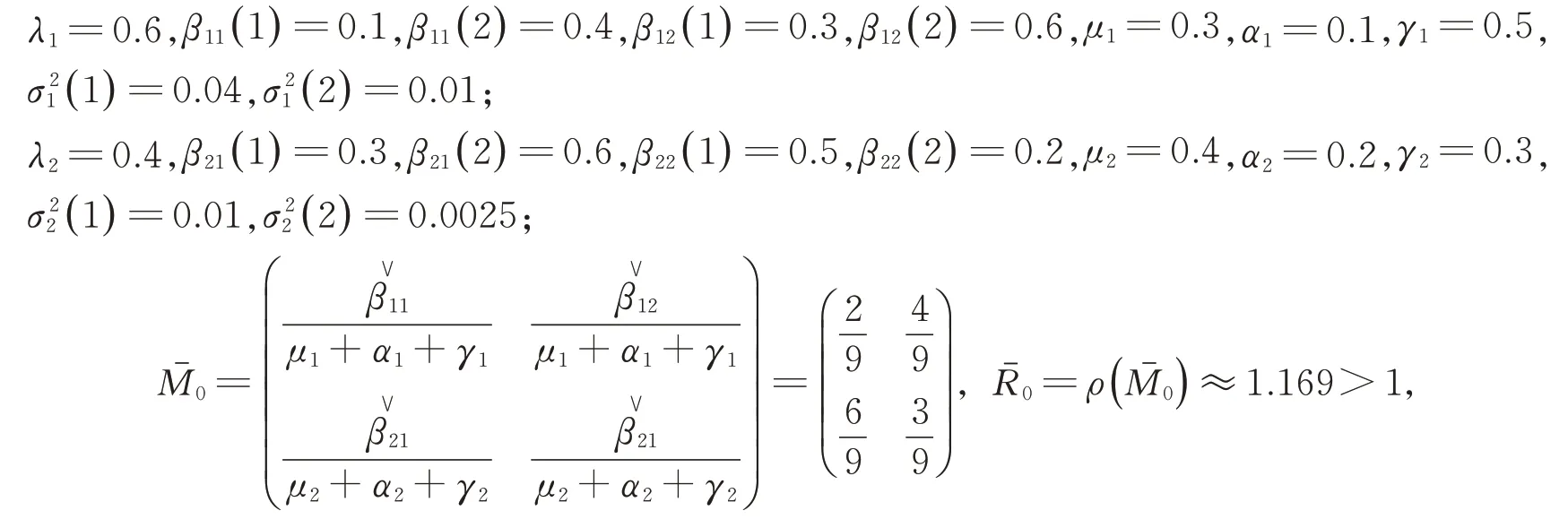
且

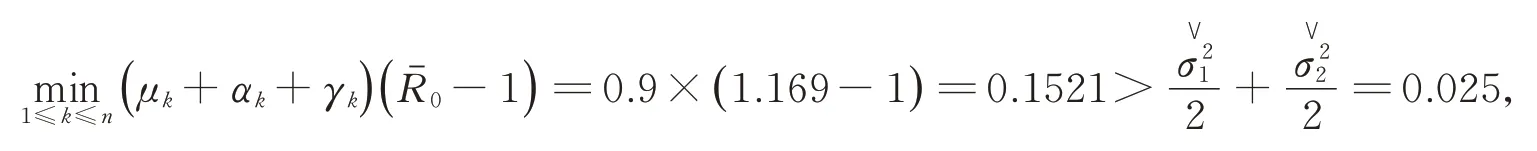
滿足定理3中的條件，此時傳染病持久存在。

4 結論

本文研究一項具有標準發生率和Markov切換機制的隨機多群組SIR傳染病模型。通過構建Lyapunov函數和運用隨機分析學理論，討論了模型的全局正解的存在唯一性。其次，文中建立了傳染病滅絕和持久的充分條件：

如果下列任意一個條件成立，

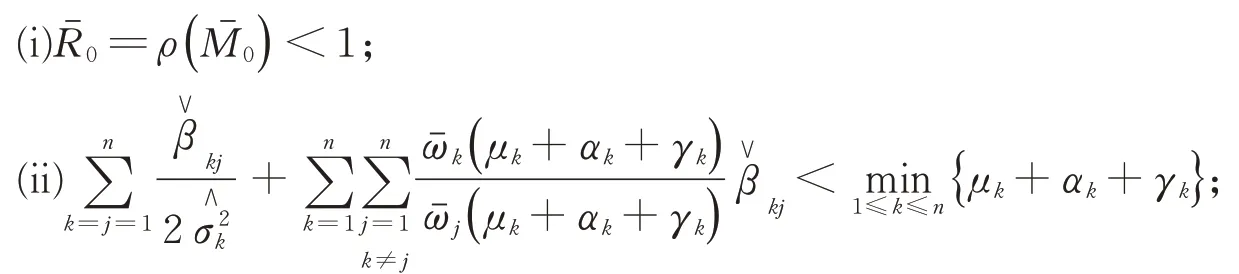
則傳染病Ik(k=1,2,…,n)依概率以1滅絕。

最后，文章用例子驗證理論研究的合理性。