基于信息熵度量的局部線性嵌入算法

劉 均, 宮子棟, 吳 力

(1. 東北石油大學 電氣信息工程學院, 黑龍江 大慶 163318； 2. 大慶油田有限責任公司 天然氣分公司培訓中心, 黑龍江 大慶 163453)

在現代工業環境中, 隨著數據采集設備不斷地進行更新迭代, 采集的數據通常具有高維特征, 致使機器學習算法出現兩個問題： 1) 隨著維數的增加, 計算量會呈指數倍增長, 降低了算法的計算效率[1]； 2) 維數災難增加了評估數據間相似性的難度, 影響算法性能. 通過將數據采用維數約簡算法進行處理, 減少數據的維度冗余[2], 是解決上述問題的有效方法, 已廣泛應用于圖像識別[3]和高維數據可視化[4]等領域.

維數約簡方法一般可分為線性降維算法[5-6]與非線性降維算法[7]. 線性降維算法基于線性映射進行降維, 僅可處理線性數據集. 例如, 目前廣泛使用的主成分分析(PCA)方法[8], 目的是找到最優投影方向, 使數據在投影方向上的方差最大且相互正交. 非線性降維算法通過非線性映射或局部線性變換處理復雜流形, 常見的算法有核化線性降維(KPCA)[9]、 等距特征映射(Isomap)[10]和局部線性嵌入(local linear embedding, LLE)[11-12]等, 其中LLE算法利用局部線性重構權重系數表示局部結構, 能保留數據的本質特征, 且算法參數選擇較少, 計算復雜度相對較小、 易實現, 因此被廣泛應用[13-16].

在LLE算法中, 構建最優鄰域進行低維重構是保持數據拓撲結構不變的關鍵, 而鄰域的結構挖掘取決于空間距離度量方法[17]. Daza-Santacoloma等[18]提出了一種相關誘導度量, 使用類標簽作為額外信息估計近鄰點, 以減輕距離差異給近鄰點選擇帶來的影響; Liu等[19]提出了一種快速識別k近鄰的方法, 通過求取相對方差和均值差形成表征相鄰點數據分布的空間相關指數, 得到最佳k值選擇鄰域； 文獻[20]提出了一種cam加權距離, 具有方向和尺度自適應性, 能充分利用原型間關系的相關信息. 上述算法在對空間度量方式的改進方面都取得了顯著成效, 但目前在實際工程應用中, 由于采集到的大多數是非對齊數據, 當采用歐氏距離[21]度量非對齊數據時, 過于關注特征數據間的對應關系, 故受數據位置差影響較大, 難以構造最優鄰域結構, 從而影響了算法的計算精度.

為解決上述問題, 本文利用信息熵度量[22]統計每個樣本點的概率分布[23], 得到數據的混亂程度, 排列后進行近鄰點選擇, 構造最優鄰域. 實驗結果表明, 基于信息熵度量的局部線性嵌入(ILLE)降維效果更好, 分類更精確, 聚類效果更緊湊.

1 局部線性嵌入

局部線性嵌入是將高維數據通過局部的線性關系表示, 即將高維數據樣本點X映射到低維空間中進行重構, 如圖1所示.實驗結果表明, 局部線性嵌入在圖像或其他不封閉流形上降維效果均較好.

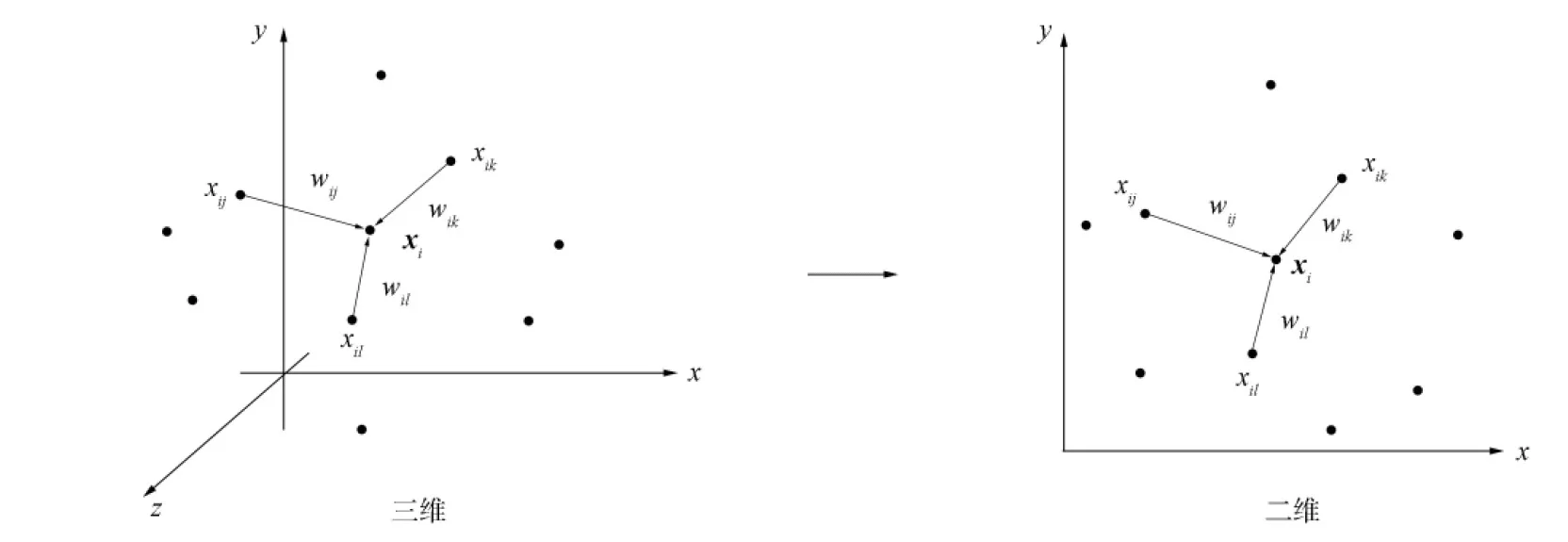
圖1 局部線性嵌入示意圖Fig.1 Schematic diagram of local linear embedding

首先需要確定近鄰點樣本個數以線性表示中心樣本點, 假設該值為k, 通過歐氏距離度量選擇某個樣本的k個最近鄰.在尋找某個樣本xi的k個最近鄰后, 再求出xi與這k個最近鄰之間的線性關系, 即找到線性關系的權重系數, 從而變為一個回歸問題.假設有m個n維樣本(x1,x2,…,xm)用均方差作為回歸問題的損失函數, 即

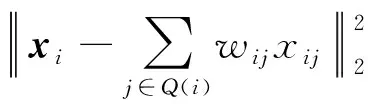
(1)

其中Q(i)表示i的k個最近鄰樣本集合.對權重系數wij做歸一化的限制, 即權重系數需滿足：

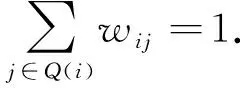
(2)

將式(2)代入式(1)中矩陣化為

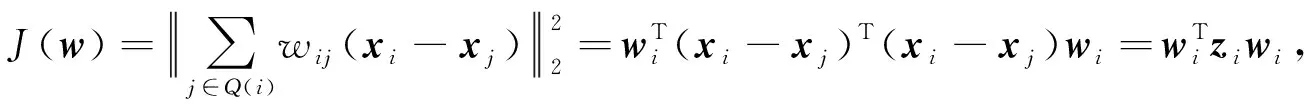
(3)

其中zi=(xi-xj)T(xi-xj),wi=(wi1,wi2,…,wik)T.然后利用Lagrange乘子法, 對式(1)求解如下:

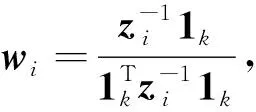
(4)

其中1k表示k維全1向量.利用wij重構向量y, 使得最小化二次型J(y)為

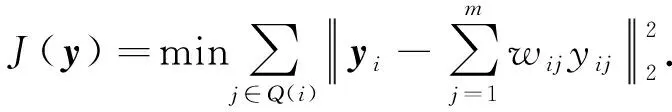
(5)

引入約束條件：

令M=(I-w)T(I-w), 則式(5)可轉換為

J(Y)=tr(YMYT).

(6)

計算M的(m+1)個特征向量, 構成LLE的新低維嵌入坐標.

2 信息熵度量

信息熵解決了信息的度量化問題. 信息熵越大表明樣本數據分布越分散(分布均衡), 信息熵越小則表明樣本數據分布越集中(分布不均衡). 針對LLE在特征提取中使用歐氏距離選擇近鄰點時存在受非對齊樣本位置差影響過大的問題, 本文提出一種基于信息熵度量的局部線性嵌入算法. 給定一個高維數據集X=(x1,x2,…,xN)∈D×N, 其中xi(i=1,2,…,N)表示任意樣本點, 具有D個特征,xi=(xi1,xi2,…,xiD)∈D×1, 其中D表示特征數目.為選擇樣本xi的鄰域, 首先需求出xi中每個特征xij出現的概率P(xij)(j=1,2,…,D), 然后計算出特征集xi的信息熵值E(xi):

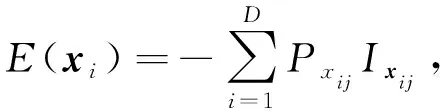
(7)

Ixij=log2Pxij,

(8)

由于信息用二進位編碼, 故log對數函數底數取2. 根據式(7),(8)計算出的原始數據集X中所有的樣本點的信息熵值表征每個樣本點的特征混亂程度.將樣本xi的熵值與數據集X中其他樣本點的熵值做差, 表示為

θ=E(xi)-E(xl),l=1,2,…,N.

(9)

按式(9)計算結果, 選擇前k個最小差值對應的樣本點構造局部鄰域.根據xi的k個近鄰點, 計算重構權重系數:

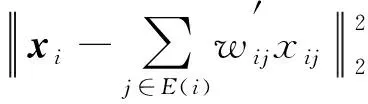
(10)

ILLE算法描述如下.

輸入： 高維樣本集X=(x1,x2,…,xN)∈D×N, 低維維數d, 近鄰點個數k；

輸出： 樣本集X對應的低維嵌入結果Y；

步驟1) 利用式(7),(8)計算xi(i=1,2,…,N)的信息熵值；

步驟2) 根據式(9)計算熵差, 從小到大排列后選出前k個差值所對應的樣本點構造xi的鄰域；

步驟3) 根據式(10)計算樣本數據的局部重構權重；

步驟4) 通過在低維空間中保持權重系數不變, 利用式(5)計算出原始數據集X對應的低維嵌入結果Y.

ILLE算法參數選擇方法如下：d為低維維數, 從低維到高維逐漸增加；k為近鄰點數目, 值越大計算量越大.ILLE算法流程如圖2所示.

圖2 ILLE算法流程Fig.2 Flow chart of ILLE algorithm

3 實驗結果與分析

為驗證本文方法的有效性, 在標準軸承故障數據集和從實際操作臺上采集的軸承數據集上進行可視化結果分析、 量化聚類分析、 不同度量方法的對比實驗及精度對比實驗, 并分析各項實驗結果.

3.1 數據集

實驗采用的數據集1為國美凱斯西儲大學(CWRU)軸承數據中心網站上的應用于故障診斷基準數據的數據集, 該軸承數據集包括正常狀態、 滾珠狀態、 內圈故障和外圈故障4種類型的數據, 其中每種數據包含100個樣本. 故障軸承直徑為0.017 78 cm, 采樣頻率為12 kHz, 電機轉速為1 720 r/min, 截取1 024個特征作為樣本數據, 即維數為1 024.

數據集2(DATA2)為東北石油大學智能儀器研發中心實驗室自采數據集, 振動信號由加速度計和模擬量采集模塊采集, 如圖3所示. 采樣頻率為1 kHz, 電機速度為1 400 r/min, 數據維數為1 024.

圖3 數據采集平臺Fig.3 Data acquisition platform

3.2 可視化結果

第一組實驗將ILLE算法與局部切空間排列算法(LTSA)、 LLE算法和主成分分析算法(PCA)3種降維算法在CWRU數據集中進行可視化比較, 實驗結果如圖4所示, 其中紅點表示正常數據, 綠點表示內圈故障數據, 藍點表示滾珠故障數據, 黑點表示外圈故障數據.

圖4 不同降維方法的可視化結果Fig.4 Visualization results of different dimensionality reduction methods

由圖4可見, LLE和LTSA算法在特征選擇上有較大重疊, 而PCA算法雖然分類效果顯著, 但是類內距離較大, 聚類效果較差. ILLE算法綜合結果優于其他3種算法, 在聚類和分類效果上都有更好的表現.

3.3 量化聚類評價

本文使用Fisher準則[24]對所提方法進行定量分析. Fisher判據是一種比較兩個變分級數方差的靜態方法, 其定義如下:

其中Sb和Sw分別表示類間和類內的距離.F值越大, 對應算法的性能越好.

本組實驗選取LLE算法、 LE(Laplacian Eignmaps)算法、 線性判別分析(LDA)算法和PCA算法與ILLE算法作為對比算法, 分別在CWRU數據集和DATA2數據集上進行性能比較, 實驗結果列于表1, 其中F1表示通過CWRU數據集評測的結果,F2表示通過DATA2數據集測評的結果. 由表1可見, ILLE算法的F1值在CWRU數據集上遠大于其他4種對比算法, 具有良好的聚類效果. 在數據集DATA2中, PCA算法F2值大于LLE,LE和LDA算法, 但略低于ILLE算法. ILLE算法在兩個數據集上都具有良好的聚類效果, 證明了本文方法的有效性.

表1 定量聚類評價結果

3.4 不同度量方法對比實驗

實驗對比LLE算法在使用各距離度量方法上的差異, 并與信息熵度量進行比較, 實驗結果如圖5所示. 由圖5可見： 在使用Manhattan距離和Chebyshev距離度量時, 數據的聚類和分類效果均較差, 數據分散且混亂； 在采用歐氏距離時, 雖然聚類性有所提高, 但分類情況也不是很好, 有較多的重疊情況； 而使用信息熵作為度量, 分類性和聚類性均優于其他算法, 適合特征提取, 證明了本文算法的有效性.

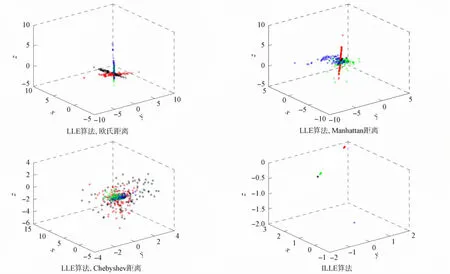
圖5 不同度量方法的實驗結果對比Fig.5 Comparison of experimental results of different measurement methods

3.5 精度對比實驗

在本組實驗中, 分別在CWRU和DATA2兩個數據集上進行算法性能對比. 先將數據集通過預處理后得到的29維特征作為原始輸入, 然后引入ILLE算法中實現特征的降維, 最后利用SVM構建故障診斷模型, 實驗結果如圖6所示. 由圖6可見, 在CWRU數據集上通過與PCA和LLE算法相比較, 發現在任何特征數目下, ILLE算法都是識別精度最高的; 而在DATA2數據集上, 雖然ILLE和PCA算法在特征數目為26～29時, 識別精度非常接近, 但整體上ILLE算法的識別精度非常穩定并較好, 表明經過ILLE方法降維后的特征可較好地表現原始高維輸入.

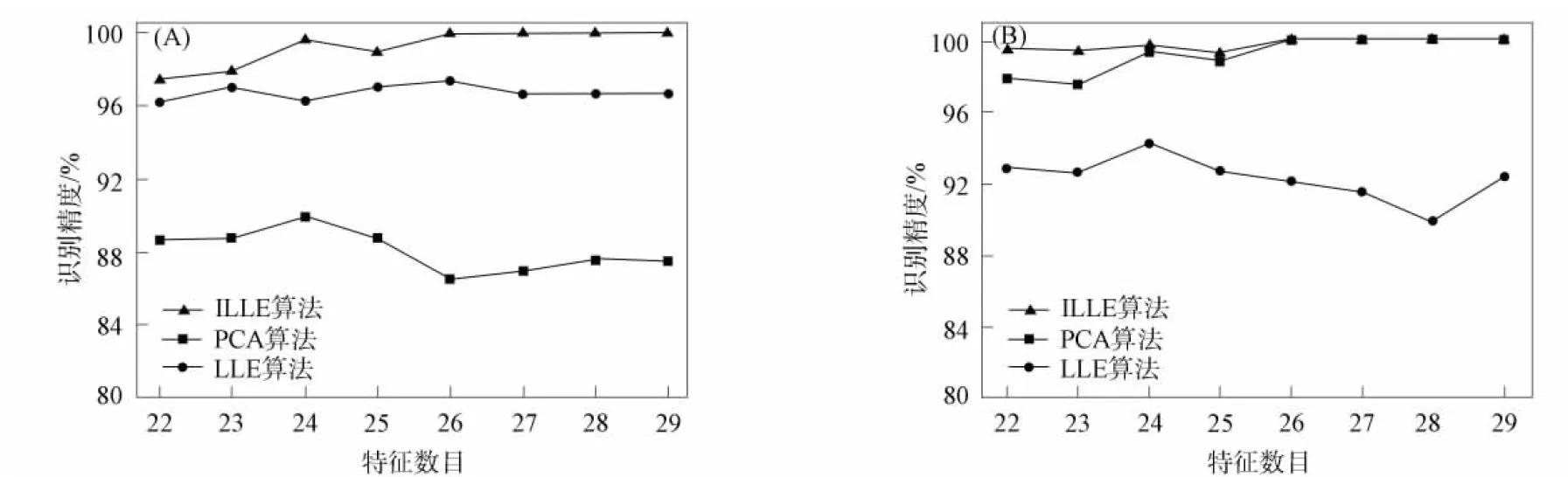
圖6 不同維數約簡算法在CWRU數據集(A)和DATA2數據集(B)上的識別精度對比結果Fig.6 Comparison results of recognition accuracy of different dimension reduction algorithms on CWRU dataset (A) and DATA2 dataset (B)

綜上所述, 本文提出了一種基于信息熵度量的局部線性嵌入方法, 通過統計每個樣本的類混亂程度構建樣本鄰域結構, 該方法避免了非對齊數據給鄰域選擇帶來的影響. 將本文算法應用到CWRU數據集和東北石油大學的自采數據集中, 得到的結果與其他降維算法進行比較, 具有更直觀的可視化結果和更高的類間類內比, 證明了本文算法的有效性.