某地鐵橫通道掌子面失穩原因分析*
歐陽鵬博,王承科,肖洪波,鐘志全,任慶國
(1.中建五局土木工程有限公司,湖南 長沙 410004; 2.中國建筑第五工程局有限公司,湖南 長沙 410004)
0 引言
新奧法隧道施工過程中,掌子面穩定是安全施工的一種保障。目前,關于掌子面穩定的研究主要包括軟弱地層掌子面穩定性分析[1]、核心土對隧道掌子面穩定性的影響[2-3]、采用新奧法施工隧道的圍巖變形控制[4]。掌子面穩定性系數也可由超前支護作用于掌子面的地基反力土坡穩定原理求得,超前支護存在最佳布置方式和最佳長度[5-7]。
本文結合湘六區間橫通道工況,分析橫通道掌子面失穩原因,進而分析小導管破壞原因。
1 Winkler地基模型
Winkler地基模型假設地基由多個獨立且滿足胡克定理的彈簧單元組成,每個彈簧上的壓力p(x,y)與其對應的位移ω(x,y)成正比,比例系數為k,其表達式為:
p(x,y)=kω(x,y)
(1)
式中:k為地基基床系數(kN/m3);p(x,y)為施加在地基上的壓力強度(kPa);ω(x,y)為p(x,y)位置上的位移(m)。
小導管超前支護力學模型如圖1所示,當l1≤l時,將小導管作為有限長度的Winkler彈性地基梁,其中l為隧道掌子面破裂面在水平方向的投影長度(m),l1為小導管在掌子面后的長度(m),a為掌子面距初期支護的距離(m)。
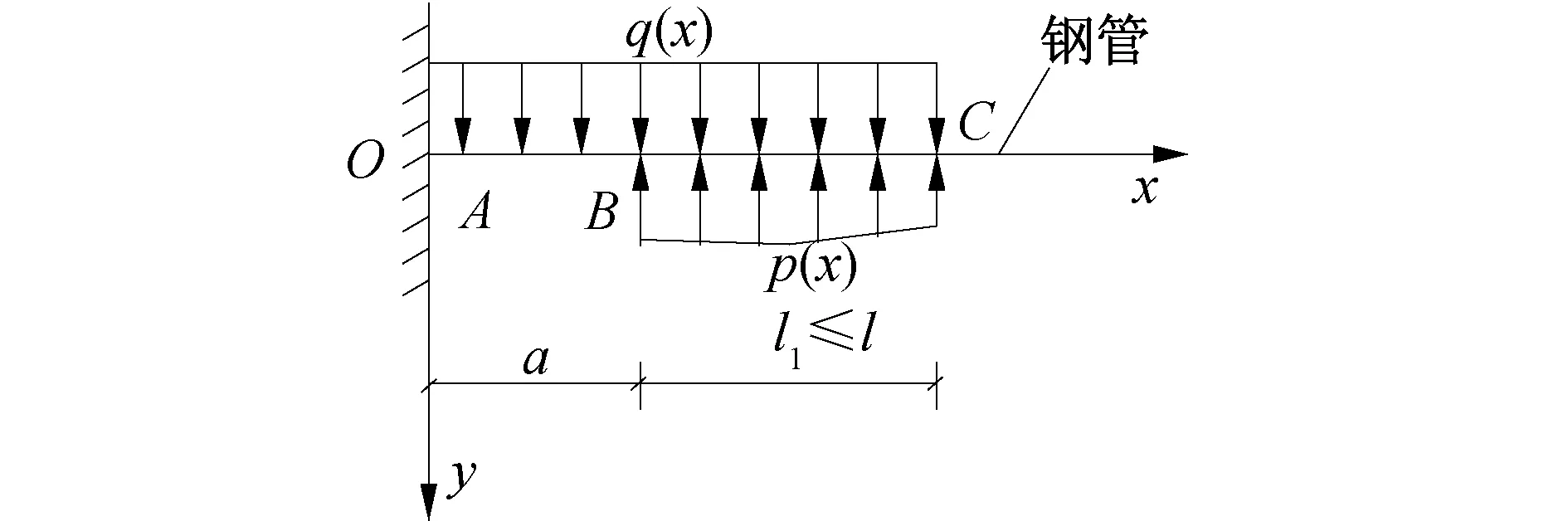
圖1 超前支護力學模型
1)微分方程
AB段:
(2)
BC段:
(3)
式中:b為梁寬度(m);q為圍巖壓力(Pa);E為梁彈性模量(Pa);I為梁慣性矩(m4)。
解微分方程求得撓度方程。
AB段:
(4)
BC段:
(5)
2)轉角方程
AB段:
(6)
BC段:
(7)
3)彎矩方程:
AB段:
(8)
BC段:
(9)
4)剪力方程
AB段:
(10)
BC段:
Q2=-EI{2λ3eλx[(-A5+A6)cosλx-
(A5+A6)sinλx]+2λ3e-λx[(A7+
A8)cosλx+(-A7+A8)sinλx]}-
shλ(x-l)cosλ(x-l)]}
(11)
式中:A1~A8為待定系數,由邊界條件ω1|x=-a=ω0,θ1|x=-a=0;ω1|x=0=ω2|x=0,θ1|x=0=θ2|x=0,M1|x=0=M2|x=0,Q1|x=0=Q2|x=0;M2|x=l=0,Q2|x=l=0可得如下方程組:
(12)
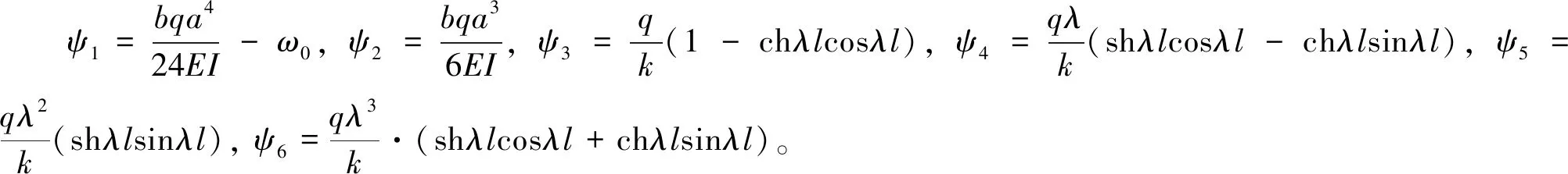
由式(12)求出待定系數A1~A8,將其帶入式(4)~(5),可得小導管任意一點的撓度,將求得的撓度代入式(1),可求得地基反力。
2 掌子面穩定性分析模型
破裂面上方巖體除受其自重外,還受到2種力:①地基反力p(x),地基反力等于小導管作用于地基的力;②圍巖壓力q(x),圍巖壓力可由q=γhq= 0.45×2s-1γω求得,其中hq為等效荷載高度值;s為圍巖級別;γ為重度;ω為寬度影響系數,ω=1+i(B-5),B為坑道寬度(m);i為B每增加1m時圍巖壓力的增減率(以B=5m為基準,B<5m時,取i= 0.2;B>5m時,取i=0.1)。小導管作用下掌子面穩定性分析模型如圖2所示。

圖2 小導管作用下掌子面穩定性分析模型
假設破裂面為潛在滑動面,穩定安全系數K為滑動面上抗滑力R與下滑力S的比值,即:
K=R/S
(13)
隧道掌子面邊坡巖體提供的抗滑力為:
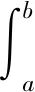
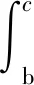
(14)
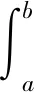
隧道掌子面巖體提供的下滑力為:
(15)
由式(13)~(15)得到穩定安全系數K為:
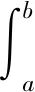
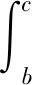
(16)
3 案例分析
3.1 工程概況
湘雅三醫院站—六溝垅站區間位于岳麓區,區間始于湘雅三醫院站,左線全長891.874m,右線全長892.91m。本區間埋深較大,最小埋深約17m,最大埋深約33m。隧道穿越范圍巖層主要為強風化、中風化、微風化板巖,局部存在構造角礫巖,區間大里程段存在F20斷裂帶。
設豎井橫通道,與區間正線垂直相交,洞身范圍主要為中風化及微風化板巖,局部存在全風化板巖軟弱夾層,橫通道采用上下臺階法開挖,上臺階分為上導坑和下導坑。橫通道上臺階第12榀開挖時掌子面失穩破壞。
勘察設計文件中橫通道右側拱頂處為中風化板巖,其初期支護按IV級圍巖設計,而在實際施工中,揭露圍巖為全風化板巖,與勘察設計文件中不符,施工時掌子面失穩破壞,如圖3所示。

圖3 掌子面失穩和小導管破壞
根據勘察設計文件,計算力學參數如表1所示。

表1 計算力學參數
橫通道上臺階上導坑高3m,埋深28m,寬6.9m,開挖進尺1.2m,即隧道未支護段長1.2m。A端(見圖1)初始位移ω=4mm。小導管采用直徑42mm、壁厚3.5mm、長3.5m的鋼管,插入掌子面前方圍巖1m。鋼管彈性模量E1=210GPa,砂漿彈性模量E2=23GPa。單根鋼管等效彈性模量E根據E=(E1I1+E2I2)/(I1+I2)求得。利用Maple數值計算軟件進行計算分析。
3.2 穩定性分析
將參數代入Winkler地基模型和掌子面穩定性分析模型中得到掌子面穩定性系數,中風化板巖掌子面穩定性系數為5.734,全風化板巖掌子面穩定性系數為0.896<1,可知掌子面在中風化板巖中非常穩定,而在全風化板巖中失穩破壞。
因掌子面失穩,不能為小導管提供地基反力,即小導管只受拱頂圍巖壓力,因此,小導管尾端彎矩急劇增加,直至破壞。
無小導管支護時,將參數代入掌子面穩定性分析模型中得到掌子面穩定性系數,中風化板巖掌子面穩定性系數為3.445,全風化板巖掌子面穩定性系數為0.564<1,可知無小導管支護時,中風化板巖和強風化板巖的掌子面穩定性系數減小。
由于圍巖情況與勘察設計文件不符,圍巖支護不利,因此建議采用地質雷達對掌子面前方圍巖進行掃描,若掌子面前方圍巖情況與勘察設計文件不符,應及時改變支護方案。
4 掌子面前方小導管長度對其穩定性的影響
掌子面前方小導管長度在破裂面水平投影范圍內時,按本文計算模型計算掌子面穩定性系數;在破裂面水平投影范圍外時參考文獻[8]的計算模型計算掌子面穩定性系數。不同圍巖掌子面前方小導管長度與掌子面穩定性系數的關系如圖4所示,其中中風化板巖中l為1.628m,全風化板巖中l為2.179m,l1≤l為有限長,l1>l為半無限長。
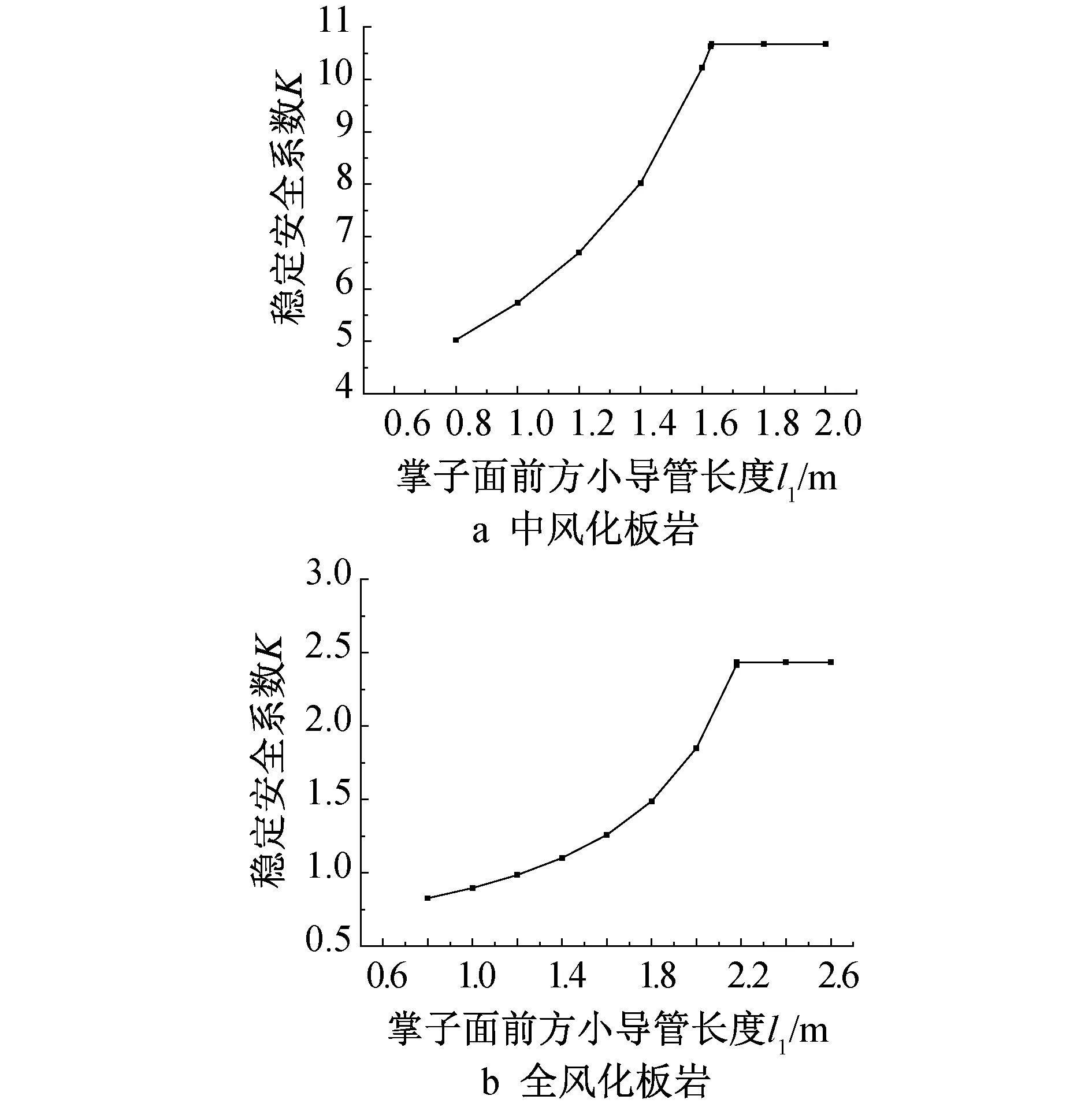
圖4 掌子面前方小導管長度對穩定性的影響
由圖4可知,全風化板巖和中風化板巖中掌子面穩定性系數隨掌子面前方小導管長度的增加先增加后趨于平穩,l1≤l時為增加段,l1>l時為平穩段。
5 結語
1)基于Winkler地基模型得到的地基反力,通過掌子面分析模型及剛體極限平衡理論,得到隧道掌子面安全穩定系數計算方法,當穩定安全系數K<1時,隧道掌子面易失穩破壞。
2)通過計算穩定安全系數,當隧道圍巖由中風化板巖變為全風化板巖后,隧道掌子面穩定性系數<1, 掌子面易失穩,且在實際施工中,掌子面產生破壞,證明計算方法正確。
3)掌子面穩定性系數隨小導管長度的增加先增大后趨于平穩,l1≤l時,掌子面穩定性系數增加幅度隨掌子面前方小導管長度的增加而增加;l1>l時,其值趨向平穩。在全風化板巖條件下,l1>1.3m時,掌子面穩定性系數>1,因此可采取增加小導管長度的方式保持隧道掌子面穩定。

