基于多智能體強化學習的電力市場競價模型
黃飛虎,李沛東
(1.四川中電啟明星信息技術有限公司,成都 610000;2.四川大學計算機學院,成都 610000)
0 引言
2015年國家針對電力體制改革發布了《關于進一步深化電力體制改革的若干意見》[1],該文件體現了國家對電力市場建設的重視和高瞻遠矚。文件說明了電力市場建設的目的,即打破現有的統一定價,通過市場競爭確定電價,充分發揮發電側、售電側、用電側各個參與者的積極性,促進我國電力系統的發展。目前我國電力市場建設還處于初期階段,截至2021年9月,我國已完成了第二批電力現貨試點工作[2]。相比于國外的電力現貨市場發展,我國的電力市場建設還有很多工作需要完善。
本文針對發電商參與電力現貨市場競價的場景,提出了基于多智能體強化學習的競價模型,為電力現貨競價的研究人員提供參考。模型中,每個發電商抽象為一個智能體,具有動作空間和狀態空間。考慮到競價過程中,每個廠商對其他廠商的競價策略以及市場出清結果的未知,模型采用了一種分散式學習算法,即Wolf-PHC,求解各發電廠商的最優策略。實驗結果實證了本文模型的有效性。
1 相關工作
電力現貨,即現貨市場,是電力市場的組成部分。電力市場中除了電力現貨之外,還包括中長期市場、容量市場、期貨市場以及衍生品市場等[3]。現貨市場涉及日前、日內、實時等短時間的電能交易。實時電能交易主要以小時為單位,主要解決超短期的電能缺乏和阻塞問題。現有的電力現貨競價策略可以分為三大類,一是基于成本的競價策略,二是基于預測算法的競價策略,三是基于博弈算法的競價策略。
(1)基于成本的競價策略是一類經典的方法。這類方法以經濟學為基礎分析發電成本,進而完成競價。比如,文獻[4]提出的報價策略主要考慮發電成本分析與系統邊際電價之間的關系,其中系統邊際電價通過預測算法得到。文獻[5]通過分析機組在不同負荷下的發電成本,討論了基于邊際成本的競價策略。
(2)基于預測算法的競價策略。這類方法首先預測競爭對手的報價或者市場出清電價,然后作出競價策略。比如,文獻[6]則主要討論單一水電廠參與的競價問題,文中提出了基于市場出清電價預測的報價策略,策略主要約束條件是可用水量和機組特性。
(3)基于博弈算法的競價策略。這類方法以博弈論、強化學習為基礎,實現最優競價策略。相比基于預測的競價策略,這類方法具有更好的效果。博弈過程是參與者在相互作用中尋找最優策略的過程,這與電力市場參與者之間的競價過程十分類似。因此,有一些學者基于博弈論構建競價決策方法。比如,文獻[7,8]對風光互補發電系統進行了競標分析,將其建模為一個多人貝葉斯博弈問題,進而提出了基于貝葉斯博弈理論的競價模型。強化學習因其扎實的理論基礎,在很多應用場景(比如推薦系統、智能駕駛等)得到了應用。在電力現貨中,也得到了學者們的廣泛關注。比如,文獻[9]將電力市場建模為信息有限的場景,提出了基于強化學習自動機的模型。模型中,作者利用重復博弈建模發電商與市場的反饋過程。文獻[10]針對中長期電力市場發電商報價問題,采用A3C算法進行了建模仿真,并討論了運營效率。
2 競價模型構建
2.1 問題定義
報價策略算法的任務是給出合適的報價策略,實現利潤最大化。從任務特點來說,發電廠商報價策略需考慮發電成本、機組出力等自身情況,推斷日期(或實時)市場邊界條件以及競爭對手的報價情況進而做出決策。從科學問題來說,報價任務可以定義為帶約束條件的優化問題,即:
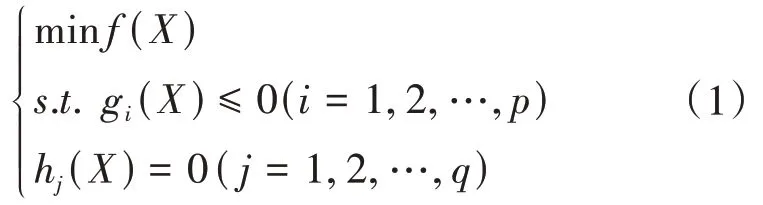
其中,約束條件包括機組運行特性(比如機組優先電量約束、機組出力上下限約束、機組爬坡約束等)、市場邊界條件(比如線路潮流約束、斷面潮流約束、電量空間邊界等)。
2.2 模型描述
本文將各發電商建模為智能體,電力市場出清建模為環境,將發電商報價決策問題轉化為一個多智體強化學習求解問題,如圖1所示。各發電商根據發電成本、負荷需求和機組運行特性等約束條件給出最優報價。在交易中心收到所有發電商的報價之后,結合網絡拓撲參數、潮流約束和負荷需求等因素進行出清,最后將出清結果反饋給各發電商。
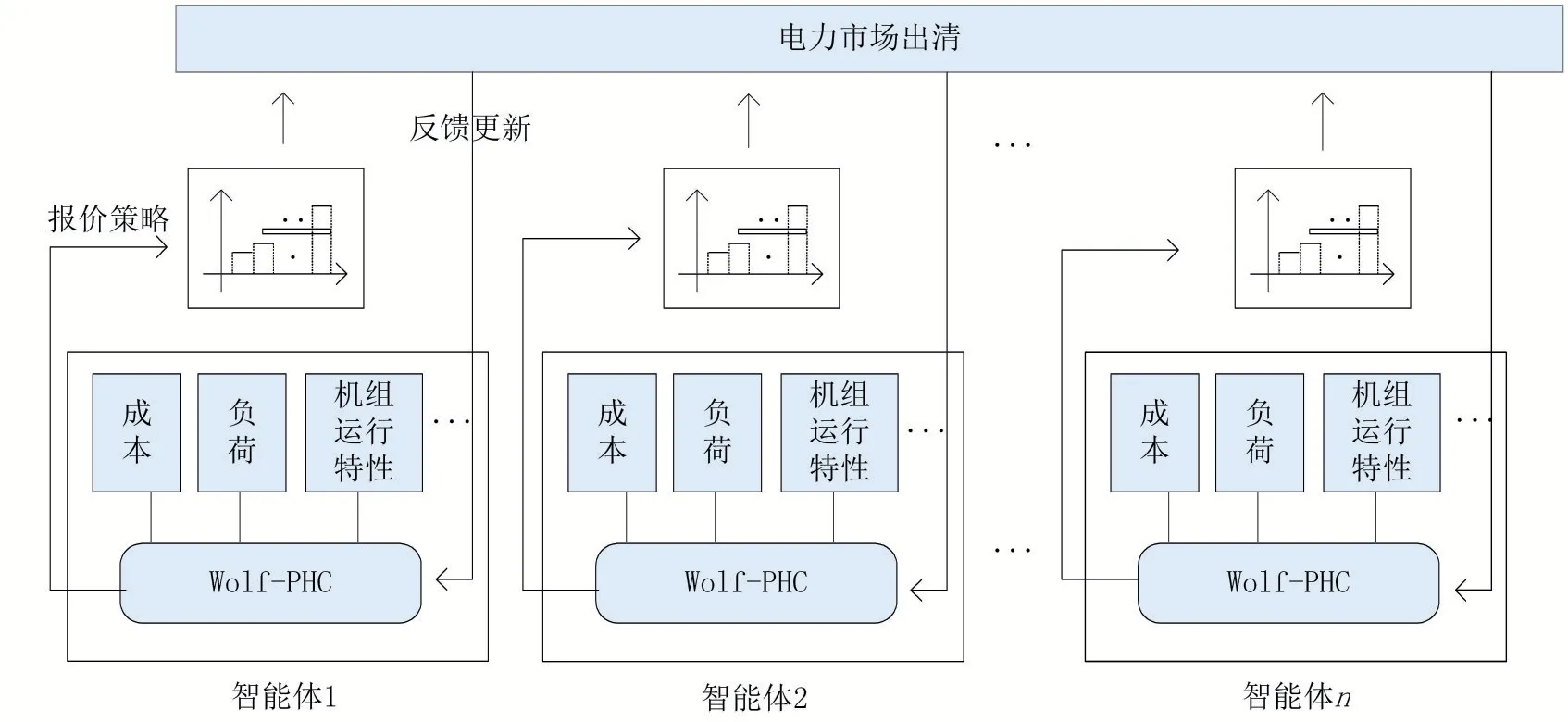
圖1 模型框架
結合強化學習方法,相關定義如下。
定義1智能體。用集合G={g1,g2,…,gn}表示,在電力現貨日前市場中,發電商i為一個智能體(即gi),各智能體之間具有競爭關系。
定義2動作。用集合A={a1,a2,…,an}表示,本文定義動作ai為發電商可選擇的第i種報價曲線。
動作ai與發電商機組的出力區間相關,給定發電商的出力區間為[Pmin,Pmax],報價區間數為d段,則動作ai的報價曲線為:

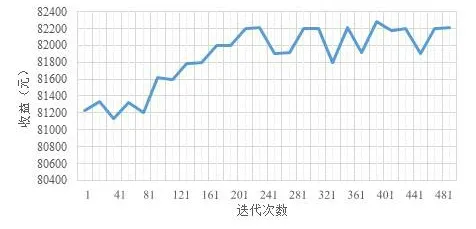
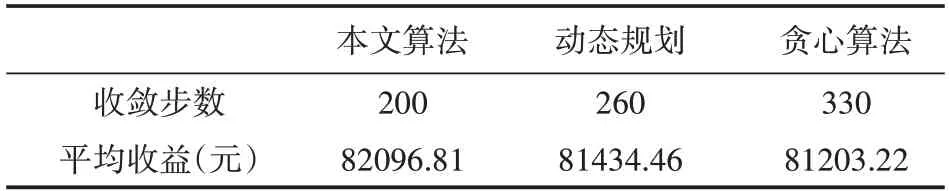
其中x表示出力,將出力區間[Pmin,Pmax]均分為d段,k1到kd為出力區間的分段標簽,ci,?表示對應區間的價格,滿足ci,1≤ci,2 定義3狀態。用集合S={s1,s2,…,s n}表示,本文定義發電商的出力情況為狀態。 本文根據發電商的出力區間為[Pmin,Pmax]將狀態離散化為n個區間,即S={[Pmin,P1),[P1,P2),…,[Pn-1,Pmax]}。 定義4回報。用r表示,本文定義回報即發電商報價后可以獲得的收益。ri即智能體i在當前狀態si下選擇動作ai之后獲得的收益。 不同類型的發電商有不同的發電成本,但計算方式均與中標電量、中標價格和成本相關。 定義5環境。用E表示,本文定義市場出清為環境,其決定各發電商在采取特定動作后的回報。 本文基于安全約束經濟調度(SCED)進行出清,其公式如下: 其中,機組的總臺數是N,總時段數為T,機組i在時段t的出力用pi,t表示,C i,t(pi,t)為機組i在時段t的運行費用,是與機組申報的各段出力區間和對應能量價格有關的多段線函數;網絡潮流約束松弛罰因子用M L S表示;M C為機組優先電量約束松弛罰因子。公式中,針對電網安全問題,重點考慮了線路潮流和斷面潮流的約束。首先,線路l在時段t的正、反向潮流松弛變量,即和;然后是斷面s在時段t的正、反向潮流松弛變量,即sls+s,t,s l s-s,t;最后,考慮了機組i在時段t的機組優先電量松弛變量s l ci,t。 定義6策略。用π表示,其定義了一個特定時刻智能體的行為方式,即發電商在當前出力狀態下該采取何種報價動作。 定義7狀態-行為值函數。用Q表示,該函數刻畫了智能體在長期狀態下對于某個狀態或者行為的偏好。 算法1智能體i的學習算法。 初始化: 學習率α=(0 ,1],δw∈( 0,1]且δl>δw; 折扣因子γ∈(0,1);探索率ε; 狀態-行為值函數Qi(a)=0; 重復: (1)根據具有某一探索率ε的策略πi(a)選擇報價動作并提交給市場。 (2)觀測直接回報ri。 (3)更新Qt+1i(a),計算公式為: (4)更新策略πti+1(a),計算公式為: 其中, 在實際報價過程中,各發電廠商不知道其他競爭對手的策略,也不知道市場出清的信息,即回報函數。因此,本文采用Wolf-PHC算法求解報價最優策略。該算法中,各智能體只需知道自身的行為和每次獲得的回報。在算法訓練階段,重復執行步驟(1)~(5)直至達到最大迭代次數或滿足特定終止條件。當算法訓練結束之后,則可以使用算法進行實際報價。 實驗中地區的負荷數據,本文采用的數據集1數據集:https://www.eia.gov/electricity/gridmonitor/dashboard/electric_overview/US48/US48源于美國能源信息署的公開數據平臺,本文下載了紐約市2015年7月—2021年4月的數據。數據間隔時間以小時為單位。訓練過程中10天出清為一次迭代,每次迭代結束后記錄各發電商10天的收益及所有發電商10天的總收益。 仿真實現對5節點3發電商系統進行模擬,每個發電商擁有一臺火力發電機組,驗證指標為每次迭代后的各發電商收益和總收益。設置的發電商機組信息如表1所示。 表1 發電商機組信息 每次出清發電商收益ri的計算公式為: 其中cost=a1(x‘)2+a2(x‘)+a3,x‘為中標出力,c‘為中標電價,a1,a2和a3分別是成本系數,實驗中其設置信息如表2所示。 表2 成本系數設置 實驗記錄了總體的收益變化過程以及各發電商的收益變化過程,如圖2和圖3所示。 圖2 總體收益變化 圖3 各智能體收益變化 從實驗結果來看,各發電商的收益隨迭代次數增加,逐漸提高,最后達到穩定狀態。這表明本文模型求解的最優策略能夠使各發電商收斂到各自的納什均衡狀態。 此外,表3統計了本文模型與貪心算法、動態規劃算法的收斂步數和收益比較。從實驗結果來看,本文采用的基于Wolf-PHC求解算法,比動態規劃和貪心算法具有更快的收斂速度,而且也能保證整個系統達到較大的收益。 表3 算法對比 針對電力市場的報價場景,本文提出了基于多智能體的強化學習報價策略。特別地,在策略求解時,針對各智能體無法知道對手策略以及回報函數的情況,提出了采用Wolf-PHC算法的思路。從實驗結果來看,本文模型是可行的。在未來的工作中,本文作者認為應該從模型可信性的角度構建競價模型。具有可信度高的模型,更容易讓競價操作者接受且認可模型給出的策略。從另一方面來說,現貨市場的競價涉及參與方的利益,因此只有可信度高的模型才能廣泛用于輔助決策。2.3 模型訓練
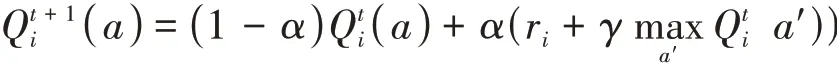
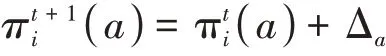
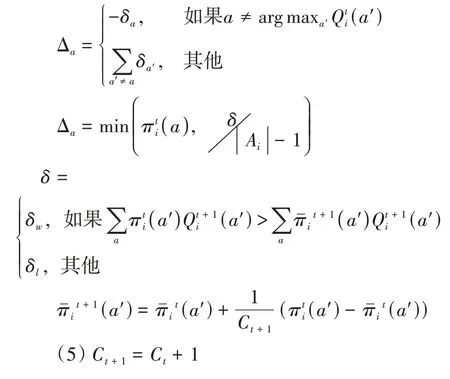
3 實驗討論
3.1 參數設置
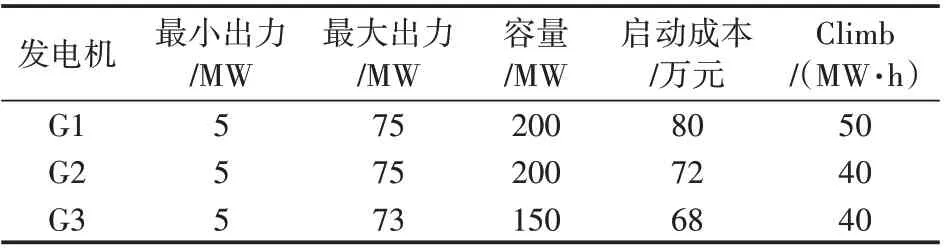


3.2 結果分析

4 結語

