智能車輛轉向姿態魯棒滾動時域估計
(浙江工業大學 信息工程學院,浙江 杭州 310023)
隨著電子安全技術的發展,主動安全系統如電子穩定控制系統(Electronic stability control system, ESC)和防抱死制動系統(Anti-lock brake system, ABS)在危及安全的情況下發揮著越來越重要的作用。例如,2015年ESC在美國挽救了1 949 人的生命,但仍有2 272 人死于各類車輛事故[1]。為了保證此類安全系統的最佳性能,獲取的車輛姿態信息必須非常準確,航向角輕微的偏差將會導致車輛偏離原來的行駛路線;質心側偏角是判斷車輛是否穩定的關鍵依據;橫擺角速度是車輛動力學控制系統進行控制決策的主要依據。現有的車輛姿態測量數據來源主要有傳感器、陀螺儀和全球導航衛星定位系統[2-5]。然而,在測量過程中,車輛姿態的數據通常會受噪聲的污染以及環境的影響,難以精確或者經濟地測量車輛姿態,這就產生了對可靠的在線估計算法的需求。
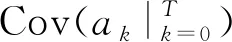
1 問題描述
智能車輛轉向系統如圖1所示。圖1中XOY為慣性坐標系;a和b分別為車輛質心到前軸和后軸的距離;Fyf和Fyr分別為車輛前輪和后輪輪胎側向力;δf為前輪轉向角;v為車輛速度,vx為車輛縱向速度,vy為車輛橫向速度;β為質心側偏角;r為橫擺角速度。
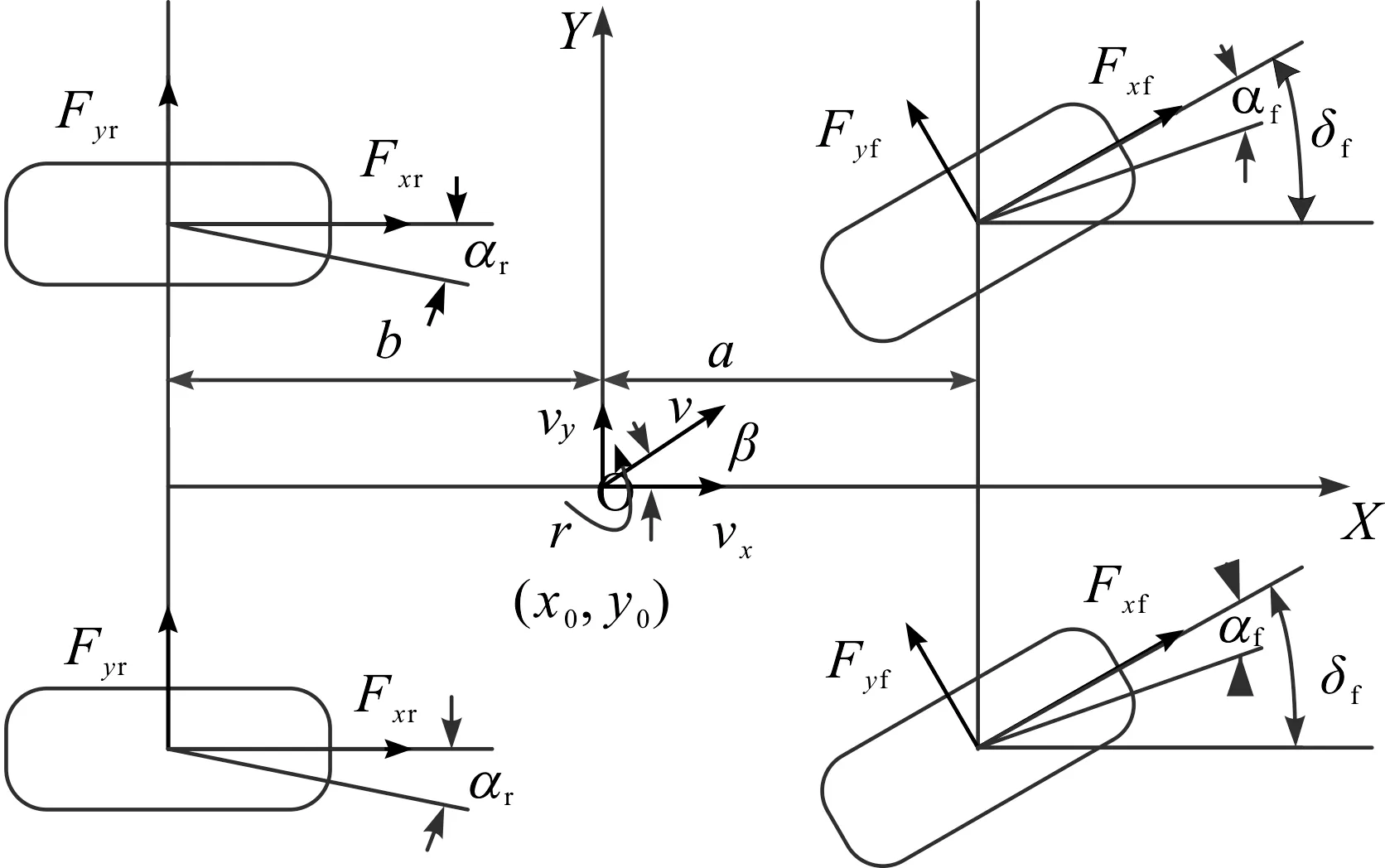
圖1 車輛轉向系統模型Fig.1 The model of vehicle steering system
在車輛動力學建模中,為簡化模型,通常忽略空氣動力學和懸架俯仰運動的影響,假設縱向速度在短時間內保持不變,忽略縱向動力學,則二自由度動力學模型的數學表達式為
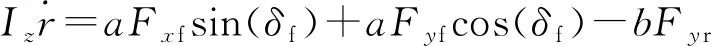
(1)
式中:m為車輛質量;Iz為車輛繞z軸的轉動慣量;Cf和Cr分別為車輛前輪和后輪側偏剛度。在車輛側向輪胎力未達到飽和狀態時,前、后輪側向力與輪胎側偏角基本呈線形關系,其表達式分別為
(2)
在運動學建模中,假設車輛為剛體。車輛縱向位置x0、側向位置y0和橫擺角φ可分別表示為
(3)
基于小角度θ假設(θ表示每個角度,包括前輪偏轉角和前后輪胎側偏轉角),其滿足近似條件cosθ≈1,sinθ≈θ。則質心側偏角β可近似為
車輛縱向位置x0和側向位置y0可簡化為
(4)
聯合式(1,4),可得車輛轉向系統模型為
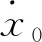
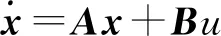
(5)
其中系數矩陣A和B分別為
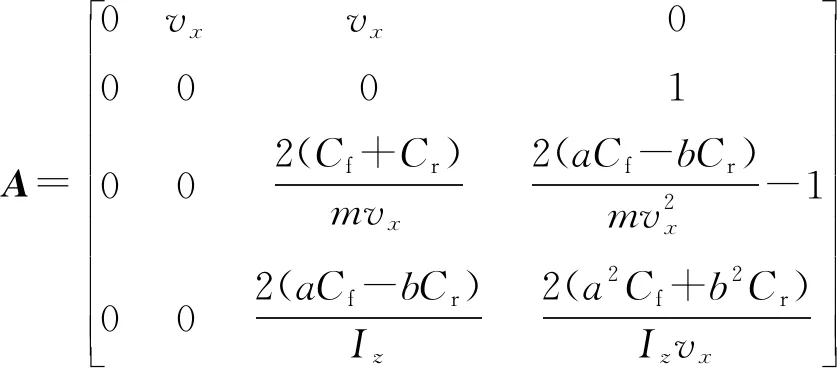
為獲取車輛姿態信息需對車輛狀態進行采樣測量。以Ts為采樣周期,將式(5)離散化得
x(T+1)=Acx(T)+Bcδf(T)+w(T)
(6)
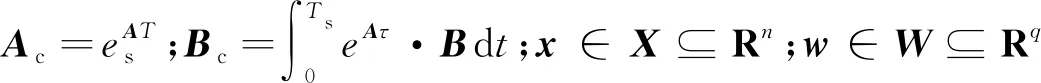
y(T)=Cx(T)+v(T)
(7)
式中:y∈Rp為T時刻收集到的車輛數據;C為已知觀測矩陣,(C,Ac)可觀;v∈V?Rp為T時刻接收到的車輛數據中所帶有的不確定噪聲,滿足vmin≤v≤vmax。
由于外界環境中不確定擾動的影響以及現有測量工具的局限性,車輛姿態信息通常難以精確地測量,或者無法經濟地測量,如測量車輛質心側偏角和外部擾動的傳感器十分昂貴,且信號的可靠性問題也尚未完全解決,使得這些信息目前在實際車輛系統中很難通過傳感器測量直接獲得。GNSS定位系統雖然可輸出航向角度信息,但其隨機噪聲大,且速度越低噪聲越大。此外,衛星信號的傳遞經常因受到地形和地物的影響而發生信號錯誤,甚至出現信號丟失等問題,因此在實際使用時經常會出現GPS無法提供信息或者所提供的信息偏差較大的問題。陀螺儀用于測量橫擺角速度,但存在幾何尺寸大、強度差、容易掉電和噪聲大等問題。現在使用較多的微機械陀螺儀的幾何尺寸雖然有所減小,噪聲問題也有所改善,但還是存在著諸如標定誤差和溫度漂移等問題,其價格隨性能的提高而增加,并且陀螺儀安裝比較麻煩,要盡量安裝在車輛質心位置,限制了它的廣泛使用。
綜合考慮硬件測量的精度、經濟性和可操作性,設計觀測器以減少對硬件的依賴非常必要。筆者基于噪聲的不確定性,設計了魯棒滾動時域估計,有效利用測量數據來估計車輛的姿態信息。
2 轉向姿態魯棒滾動時域估計
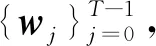
(8)
與經典滾動時域估計的目標函數不同,考慮數據測量以及傳輸過程中不確定噪聲的影響,在目標函數中添加噪聲抑制項來獲得魯棒性。參考H∞濾波的博弈近似理論[25,27],定義擾動抑制函數為
(9)
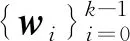
考慮數據傳輸時受不確定性噪聲的影響,基于不確定離散線性模型式(6)的魯棒全信息滾動時域估計問題(Robust full information estimation, RFIE)可表示為
(10)
s.t.xk+1=Acxk+Bcδfk+wk∈X
vk=yk-Cxk∈V
wk∈W,k∈I0∶T-1
(11)
其中目標函數為
(12)
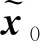
隨著時間的推移,全信息滾動時域估計需處理更多的數據,為使估計問題可行并在計算上易于處理,引入固定時域N。當T>N時,優化問題RFIE的計算時域可分為{0≤k≤T-N-1}和{T-N≤k≤T}。則目標函數式(12)可改寫為
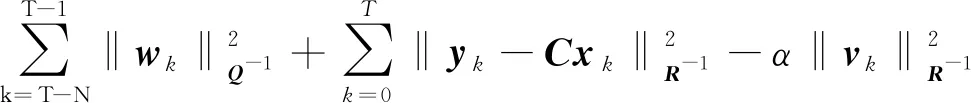
對任意可行初始狀態x0和干擾序列{wk},定義T時刻系統狀態可達集為
(13)
取s∈Sa,到達代價為
(14)
其中問題式(14)滿足約束式(11)。
為適用于車輛快速轉向,引入擾動塊結構,在估計過程中,每個時刻均對估計窗口內的擾動進行分塊,強制令同一擾動塊結構內的擾動值相等,從而減少所求的優化變量,降低計算量。
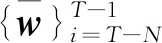
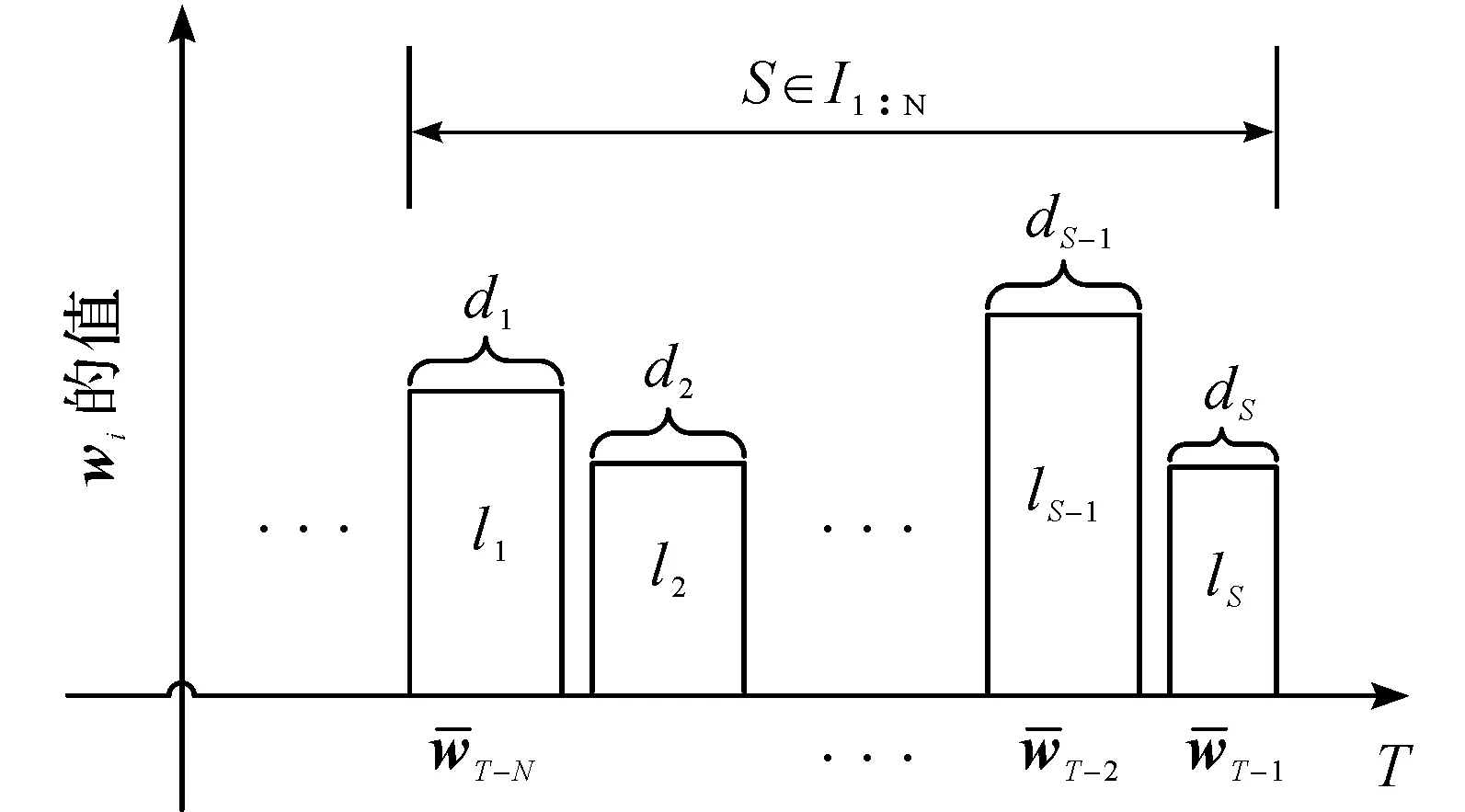
圖的塊結構示意圖Fig.2 Segment structure of
給定估計時域N>n,在T時刻求解以下帶有擾動塊的魯棒滾動時域估計問題(Blocking moving horizon estimation, BRMHE),即
(15)

(16)

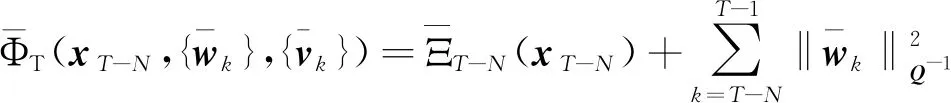
(17)
到達代價為
(18)
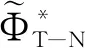
(19)
(20)
算法步驟:
1) (初始化):當T=0時,設定矩陣P0和車輛初始狀態x0,其中P0為初始條件x0的協方差矩陣。
2) 當1≤T≤N時,求解優化問題RFIE。
3) 當T>N時,求解基于擾動塊的魯棒滾動時域估計問題BRMHE。
3 可行性與穩定性分析
針對RFIE問題可行性,為符號簡便,式(12)記為
(21)
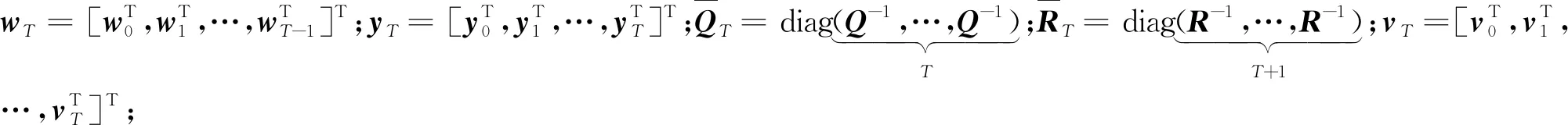
為證明算法可行性,需要以下引理來保證RFIE從x0估計x1的鞍點解的存在。
引理1[25]假設X,W,V為凸的緊集,ΦT在(x0,w0,v0)處連續。若對?v0∈V,ΦT在點(x0,w0)處為凸;對?x0∈X,w0∈W,ΦT在點v0處為凹,則函數ΦT存在鞍點。若函數ΦT為嚴格凹凸,則該鞍點是唯一的。
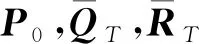
(22)
(23)
(24)

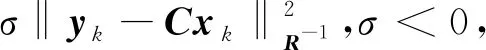
定義1[18]考慮線性系統,即
xk+1=Acxk+Bcδfk,yk=Cxk
(25)
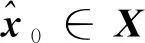

(26)
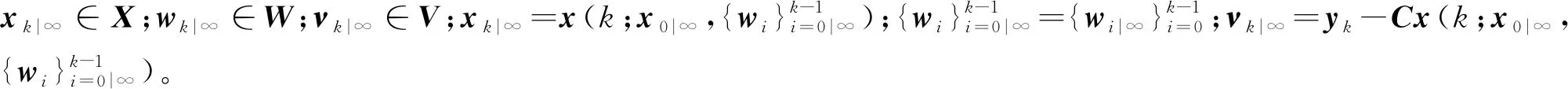
為書寫清晰,令
(27)
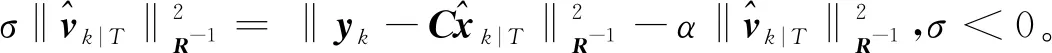

基于引理3,可獲得如下結論:
定理1考慮車輛轉向模型式(6),假設矩陣P0,Q,R正定,且假設1成立,則RFIE是漸近穩定的。
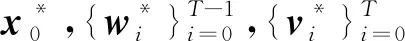
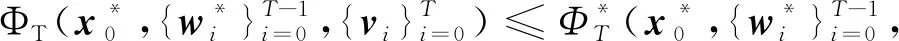
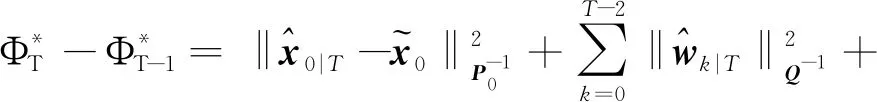

(28)
為證明穩定性,設ε>0,考慮T=n時,選擇足夠小的γ>0。若選擇δ>0,使得ρδ2<γ,則對所有T≥n有
(29)
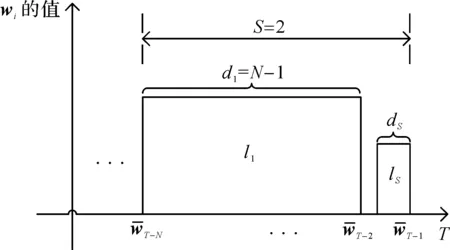
圖3 S=2時的塊結構示意圖Fig.3 Segment structure of when S=2
最大分塊長度塊結構的擾動示意圖如圖3所示。式(15~18)特例可表示為
(30)

(31)
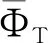
為符號簡便,式(17)記為
(32)

通過定理2和定理3討論BRMHE的可行性和引入擾動塊結構后算法的估計性能。
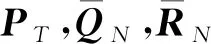
(33)
(34)
(35)
則式(15~18)在每個采樣時間均存在唯一鞍點解,其中PT由式(20)給出。
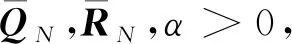
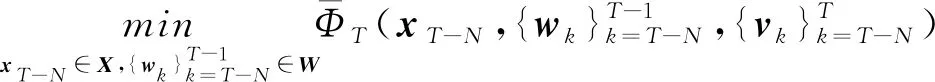
存在唯一解,即式(33,34)。
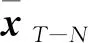
(36)
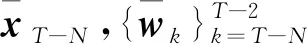
假設2系統矩陣Ac非奇異且滿足
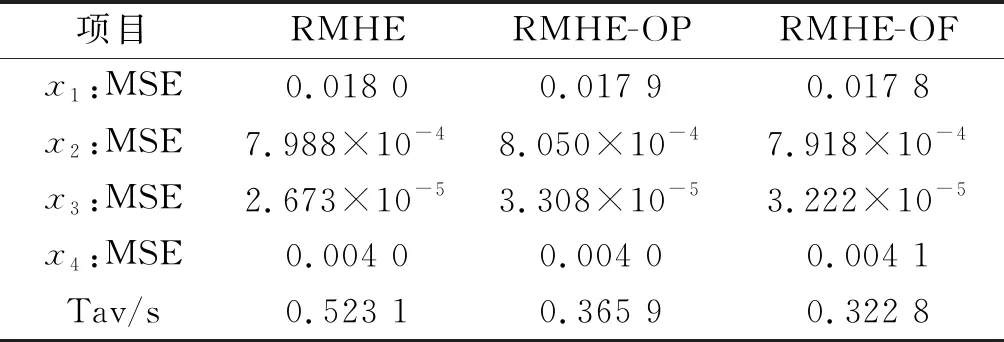
定理2若假設2成立,且S 滿足 推論1若將窗口前N-1個擾動分為S塊,BRMHE問題可行性和估計性能同樣能得到保證。 證明由定理1可知,S=2時等價解存在,且S=2為S∈I3∶N的特殊情況,故當S∈I3∶N時至少存在一組等價解。其中S=N時,BRMHE等價于不設有塊結構的RMHE。 基于推論1,若S=2時BRMHE收斂,則當S∈I3∶N時算法收斂性依然存在。故驗證S=2時(最小分塊數量)算法的收斂性。 為書寫清晰,令 (37) 引理6考慮車輛轉向模型式(6),則對任意s∈Rn,協方差矩陣PT滿足 (38) 該引理證明過程與文獻[28]引理4.4.4相似,此處省略。 定理3考慮網聯車隊模型式(6),若假設1,2成立,且N≥n,BRMHE估計器是漸近穩定的。 (39) 根據假設1,有 (40) 引理6可保證 (41) 聯合式(40,41),則有 (42) 為證明穩定性,設ε>0,考慮T=N時,選擇足夠小的γ>0。若選擇δ>0,使得ρδ2<γ,則對所有T≥N有 (43) 考慮到min-max問題具有較高的計算復雜度,因此引入坐標輪換法,分離min-max問題近似求解。min-max問題近似求解過程為 (44) 其中極小化問題滿足約束式(11)。 (45) 其中優化問題滿足約束式(11)。 若初始狀態的置信度低,則可轉至步驟2)進行多輪循環,直至連續兩次循環求得的最優解的差小于給定收斂精度。魯棒滾動時域估計最小-最大問題的近似解類似于魯棒全信息滾動時域估計。 本節考慮在同向雙車道上勻速運行的智能車輛,以評估所提算法的有效性。仿真中使用的自主車輛模型選取CarSim軟件中的C級掀背式轎車模型,車輛模型中參數以及控制器參數如表1所示。 表1 車輛及控制器參數Table 1 Vehicle and controller parameters 設自主車輛縱向行駛速度vx=25 m/s,初始位置x0=0 m,y0=-2 m,在行駛過程中設置靜態障礙,如圖4所示。采用模型預測控制(Model predictive control, MPC)規劃避障路徑[29],假設該障礙物相鄰車道有足夠的橫向空間,自主車輛經控制后,可從障礙物側面安全避開。為準確獲取車輛行駛過程中的狀態,通過測量狀態分量x1(車輛縱向位置)來估計狀態。仿真滿足假設1~4,設不確定擾動w∈[-0.1,0.1],不確定噪聲v∈[-1,1],α,P0,Q,R滿足式(33~35),分別為α=0.9,P0=diag[0.01,0.01,0.01,0.01],Q=diag[9×10-4,9×10-4,9×10-4,9×10-4],R=0.1。采樣時間Ts=0.5 s,滾動窗口N=6,初始狀態x0=[-2,0,0,0]。 圖4 MPC規劃路徑Fig.4 MPC planning path 在仿真中分別對比了3 種不同塊結構BRMHE算法:1) 標準RMHE算法(擾動不分塊);2) 將擾動分別分為長度為d1=3,d2=2,d3=1的塊結構,記為RMHE-OP;3) 將擾動以最大分塊形式劃分,即窗口內最后擾動單獨分為1 塊,其余擾動分為1 塊,記為RMHE-OF。仿真結果如圖5,6所示,圖5,6分別為各算法估計狀態軌跡圖和估計誤差圖:實線表示實際狀態軌跡;虛線、點劃線和雙劃線分別表示RMHE,RMHE-OP和RMHE-OF的仿真結果。各算法的估計均方誤差(MSE)和各算法所需的平均計算時間(Tav)如表2所示。仿真結果顯示:3 種魯棒分塊算法的估計狀態軌跡均收斂于實際軌跡,且均方誤差相近,此外在塊結構約束下,算法RMHE,RMHE-OP和RMHE-OF的優化變量分別為7,4,3 個。分析圖6和表2可知:各算法的計算速度滿足RMHE 圖5 狀態軌跡Fig.5 State trajectory 圖6 各算法估計誤差Fig.6 Estimation error of each algorithm 表2 各算法估計均方誤差(MSE)和平均計算時間(Tav) 通過結合滾動時域估計算法與博弈論方法,設計可處理不確定噪聲的魯棒滾動時域估計器。采用坐標輪換法近似求解min-max優化問題。為降低算法復雜度,在魯棒滾動時域估計算法中,通過設計擾動塊結構以及構造等價解有效降低算法計算量,從而達到快速估計的目的。仿真結果表明:設計的魯棒滾動時域估計算法能有效處理智能車輛轉向系統中帶有不確定噪聲的姿態估計問題,具有較好的抗擾性,且魯棒快速滾動時域估計算法中擾動分塊數量越少,算法估計時間越短,對于滿足可行性條件的不同分塊形式的魯棒滾動時域估計算法,均可在保證估計性能的基礎上降低計算時間。筆者主要討論車輛轉向姿態模型中基于不確定擾動與測量噪聲的估計,后續還可進一步考慮模型的結構和參數的不確定性問題。

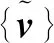
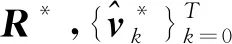
4 仿真與結果分析


5 結 論

