落角與視場約束制導控制一體化策略

郭宗易，楊曉宏，胡冠杰，郭建國，王國慶

(1. 西北工業大學航天學院精確制導與控制研究所，西安 710072； 2. 中國運載火箭技術研究院研發部，北京 100076)

0 引 言

高超聲速飛行器已成為目前世界各國搶占戰略優勢的利器。對于其制導控制系統設計，傳統設計方法是分為控制回路和制導回路兩個子系統，不考慮兩者之間的耦合關系[1]。這種分離設計的理論基礎是要求制導控制系統滿足頻譜分離條件，即姿態控制系統的時間常數遠遠小于制導系統的時間常數，但事實上高超聲速飛行器制導環節和姿態控制環節并不總是滿足該條件，因此在舵偏角的反饋控制設計中使用了姿態、過載和視線角信息等以便獲得更好的系統性能，即制導控制一體化設計(Integrated guidance and control, IGC)考慮了導彈制導系統與控制系統之間的耦合關系，根據彈目相對運動關系和導彈自身運動信息直接產生舵偏指令，驅使飛行器擊中目標[2]，并顯著減小脫靶量，有效提高制導控制系統的可靠性和穩定性[3-5]。由于飛行器的高效打擊需求和導引頭的探測能力約束，在打擊過程中需要考慮落角約束和視場角約束。目前已有較多制導律設計的相關文獻如文獻[6-8]考慮了這兩種約束，主要采用方法有障礙李雅普諾夫函數法[6]、解析法[7]和多階段切換法[8]等，但并未考慮姿態系統。目前，制導控制一體化方法大多采用滑模變結構、最優控制方法、反演設計方法等傳統控制方法，比如Li等[9]針對一體化系統，采用滑模變結構方法進行控制，變結構項會使控制量產生高頻抖振，影響系統的打擊精度，增加能耗，降低系統性能；Park等[10]采用最優控制方法，存在模型精確度不高、魯棒性較差的問題；Pei等[11]采用反演法，保證了系統的穩定性，但存在“計算膨脹”問題，存在高階導數，控制器結構復雜。以上方法多考慮落角約束或視場角約束其中一種約束情形，并未完全覆蓋兩種約束。

工程實際當中，往往需要系統在保證穩定性的同時，有較高的靈活性和自適應性，傳統的控制方法難以滿足復雜要求[12]。隨著人工智能技術的快速發展，自適應動態規劃方法開始被提出并應用到控制系統設計[13-14]。自適應動態規劃(ADP)方法是一種基于強化學習理論的先進智能控制方法，基于神經網絡的函數泛化能力，通過近似求解非線性哈密頓-雅可比-貝爾曼(Hamilton-Jacobi-Bellman，HJB)方程獲得最優控制律[15]，應用范圍廣，自適應性自調節能力強，而且能夠與干擾觀測等技術結合實現較好的魯棒性。由于ADP的強適應能力，近幾年，基于ADP方法的控制策略被應用于飛行器控制問題研究中[16-17]。郭建國等[18]針對高超聲速飛行器的姿態模型，設計反步法和ADP結合的非線性優化學習控制方法，實現系統的近似最優跟蹤。

綜上分析，目前同時考慮落角約束與視場角約束的制導控制一體化方法研究較少。因此，本文提出一種基于自適應動態規劃的新型制導控制一體化策略，其新穎之處在于：(1)不同于以往的制導約束設計方法，本文將視場角約束、落角約束和命中精度要求集成到視場角指令，從而將約束問題轉化為跟蹤問題，保證在精確跟蹤的同時即可滿足這兩種約束，而且便于結合考慮姿態系統；(2)引入基于自適應非線性擾動觀測器的不確定性估計值，設計基于ADP的制導控制一體化方法，既能夠通過保證精確跟蹤實現高超聲速飛行器的精準打擊和對落角視場角約束的滿足，又考慮制導控制模型中不確定性等多種實際因素，具有更好的技術優勢和更強的應用潛力。仿真驗證了本文提出方法的有效性，并與現有方法開展了對比研究，本文方法可以在滿足落角約束和視場角約束下實現精準打擊。

1 問題描述

首先，建立飛行器二維平面模型如下所示。

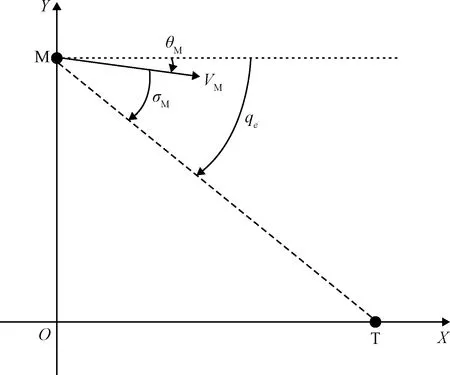
圖1 縱向平面彈目幾何關系Fig.1 Two-dimensional engagement geometry

如圖1所示，M, T分別表示導彈和靜止目標；qe,θM和σM表示視線角，彈道傾角和視場角；R表示彈目相對距離；VM表示導彈速度。運動學方程為

(1)

飛行器姿態方程為

(2)

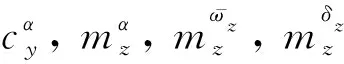
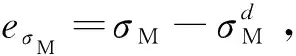
(3)

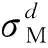
(4)

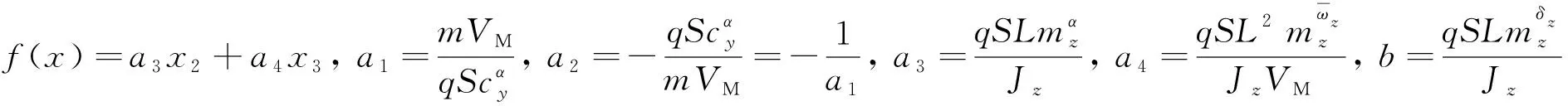
高超聲速飛行器需要考慮視場約束與落角約束來滿足探測約束與打擊毀傷效果。因此，本文的目標是針對一體化模型(4)，設計一種可以滿足視場角約束和落角約束的制導控制一體化控制器，即

(5)

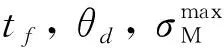
2 集成視場約束與落角約束的視場角指令設計

定義落角的誤差為

eq=qe-θd

(6)

那么飛行中需要控制上式中的變量eq，保證打擊目標時的落角。式(6)對彈目相對距離R求導，可得

(7)

基于式(7)，本文提出視場角指令為

(8)

式中：sat(·)為飽和函數，當|x|≤1時，sat(x)=x，否則sat(x)=sgn(x)。ρ和φ1為參數，滿足以下條件：

(9)

(10)

如果|eq(R)|>φ1，求解式(10)可得

eq(R)=

(11)

式中：R0和R1由R0=R(t=0), |eq(R1)|=φ1求得。式(11)的解表明|eq(R)|是嚴格遞減的，因為R也是嚴格遞減的。此外，式(11)中第2式表示當R趨于零時，eq(R)趨于零。

如果|eq(R0)|≤φ1，用R0代替式(11)第2式中的R1可得eq(R)的解。因此，在|eq(R0)|>φ1和|eq(R0)|≤φ1的情況下，當R趨近于0時，eq(R)收斂于0，滿足落角約束，從而保證精確跟蹤時必然滿足兩種約束。

3 基于ADP的制導控制一體化設計

3.1 制導控制一體化控制器設計

考慮系統(4)具有非匹配不確定性，本文引入文獻[19]提出的自適應干擾觀測器。以下是基本假設：

假設1.擾動di(t)(i=1,2,3)有界，滿足

(12)

式中：μi是正常數。

設計自適應干擾觀測器如式(13)所示

(13)

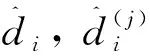
定義估計誤差為

(14)

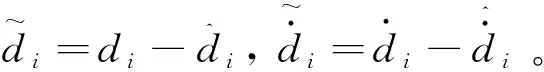
對于模型(4)，定義新變量ψ為

(15)

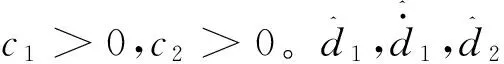
對式(15)求導可得

(16)

式中：

g(ψ)=b, Δψ=c1d1+c2d2+d3。首先給出假設：

假設 2.[15]非線性不確定項Δψ滿足條件Δψ=GT(ψ)d(ψ)，其中G(·)是表示不確定性結構的固定函數，d(·)(d(0)=0)是不確定函數，且存在已知函數h(·)(h(0)=0)滿足dT(ψ)d(ψ)≤hT(ψ)h(ψ)。

本節依據系統(16)通過構建單個網絡即評價網絡來實現，將ADP方法引入一體化非線性系統控制,設計一個控制輸入u，使它不僅能穩定閉環系統，還能最小化形式如下的代價函數

(17)

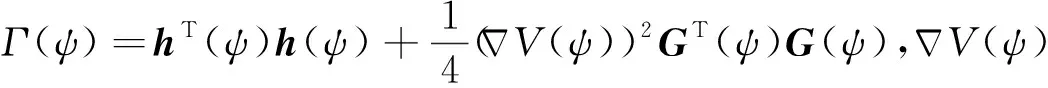
定義哈密頓函數為

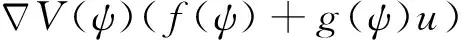
(18)

(19)

將式(19)代入HJB方程可得

(20)

由于解析求解方程(20)較為困難，接下來引入基于單一評價網絡的ADP方法來求解最優控制策略。

根據神經網絡的全局逼近性質，最優代價函數V*(ψ)可以精確地表示為

V*(ψ)=WTσ(ψ)+ε(ψ)

(21)

式中：理想權值向量W∈Rl,σ∈Rl為神經網絡激活函數，l是隱含層中神經元的個數；ε(ψ)代表神經網絡的近似誤差。于是有

(22)

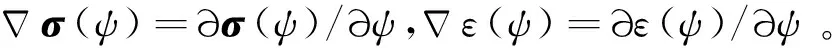
將式(22)代入式(19)可以得到最優控制形式為

(23)

由于理想權值未知，將估計的權值寫為如下形式來構建評價神經網絡進而逼近代價函數。

(24)

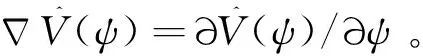
考慮式(24)，可以得到近似控制函數為

(25)

將式(25)用于式(16)，得到

(26)

(27)

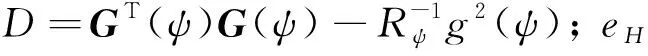
(28)

利用估計的權值向量，導出近似哈密頓函數為

(29)

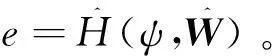
(30)

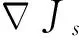
假設3.[15]針對式(16)，選取一個連續可微的李雅普諾夫函數Js(ψ)，滿足

(31)

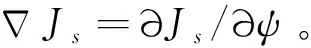
(32)

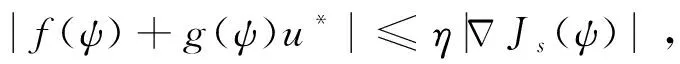
(33)

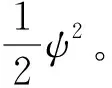
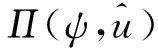
(34)

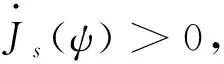
3.2 穩定性證明

(35)

(36)

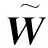
證.選擇李雅普諾夫函數為

(37)

對時間求導并代入式(36)可得

(38)

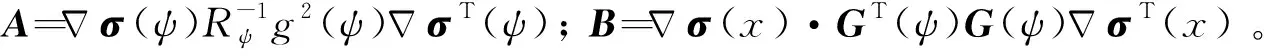
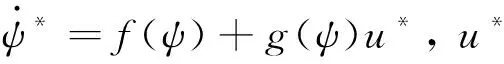
(39)

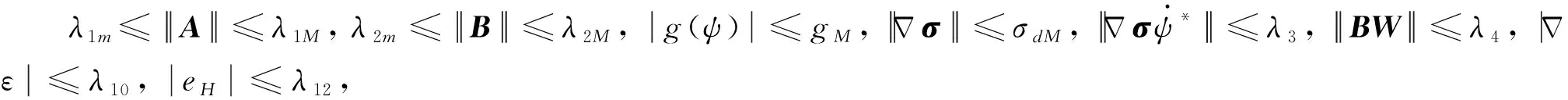
使用關系式：

(40)

(41)

則有

(42)

式中：φ+,φ-和φ1均是非零常數。同理，式(39)其余項可按同樣方式處理，得到

(43)

式中：

(44)

(45)

式中：φi,i=1,2,…,6為非零常數，保證λ7>0。

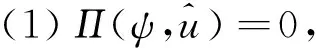
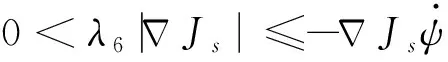
(46)

因此，如果有以下的不等式存在

(47)

(48)

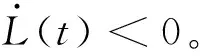
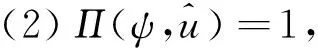
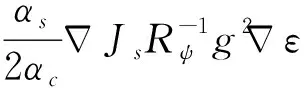
(49)

因此，如果有以下的不等式存在

(50)

(51)

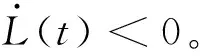
定理1分析了新變量ψ的收斂性，而下面的定理2則分析了閉環系統中狀態x1和x2的穩定性。

定理2.考慮如式(4)所示的干擾觀測器，在控制輸入(25)與評價網絡的權值式(30)作用下，閉環系統中視場角實現對指令(8)的有界跟蹤。

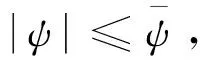
(52)

將式(52)代入式(4)可得

(53)

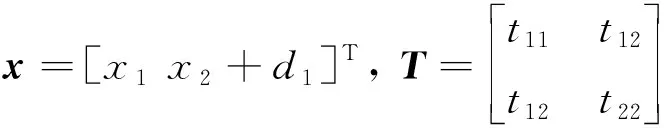
(54)

(55)

式中：q1>0,q2>0。

根據式(53)對Vx求導，得到

(56)

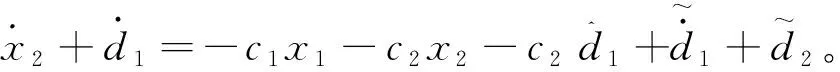
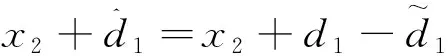
(q2|x2+d1|-μ12)

(57)

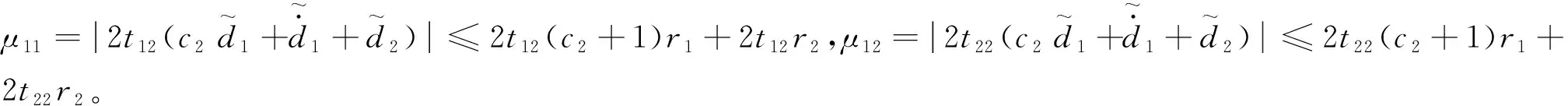
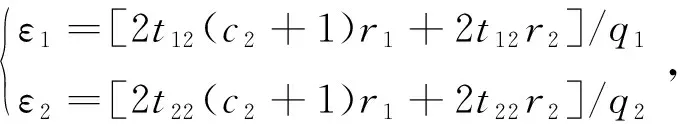
(58)

根據李雅普諾夫穩定性理論，閉環系統是穩定的，收斂范圍為

|x1|≤ε1和|x2+d1|≤ε2

(59)

因此，視場角誤差eσM=x1/a1是有界收斂的，閉環系統中視場角實現對指令(8)的有界跟蹤。同時，ε1越小，則x1越接近零，根據以上分析，在控制命令(25)下，可以保證脫靶量趨向0的情況下同時滿足視場角和落角的約束。

4 仿真校驗

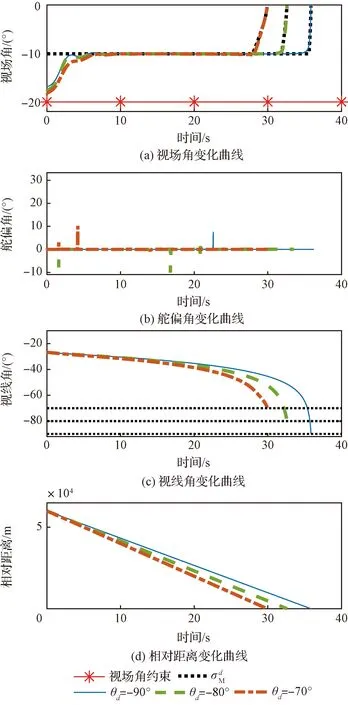
圖2 不同落角約束下，視場角、舵偏角、視線角和相對距離的變化曲線Fig.2 Curves of look angles, δz, qe, and R under different θd values

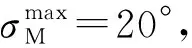
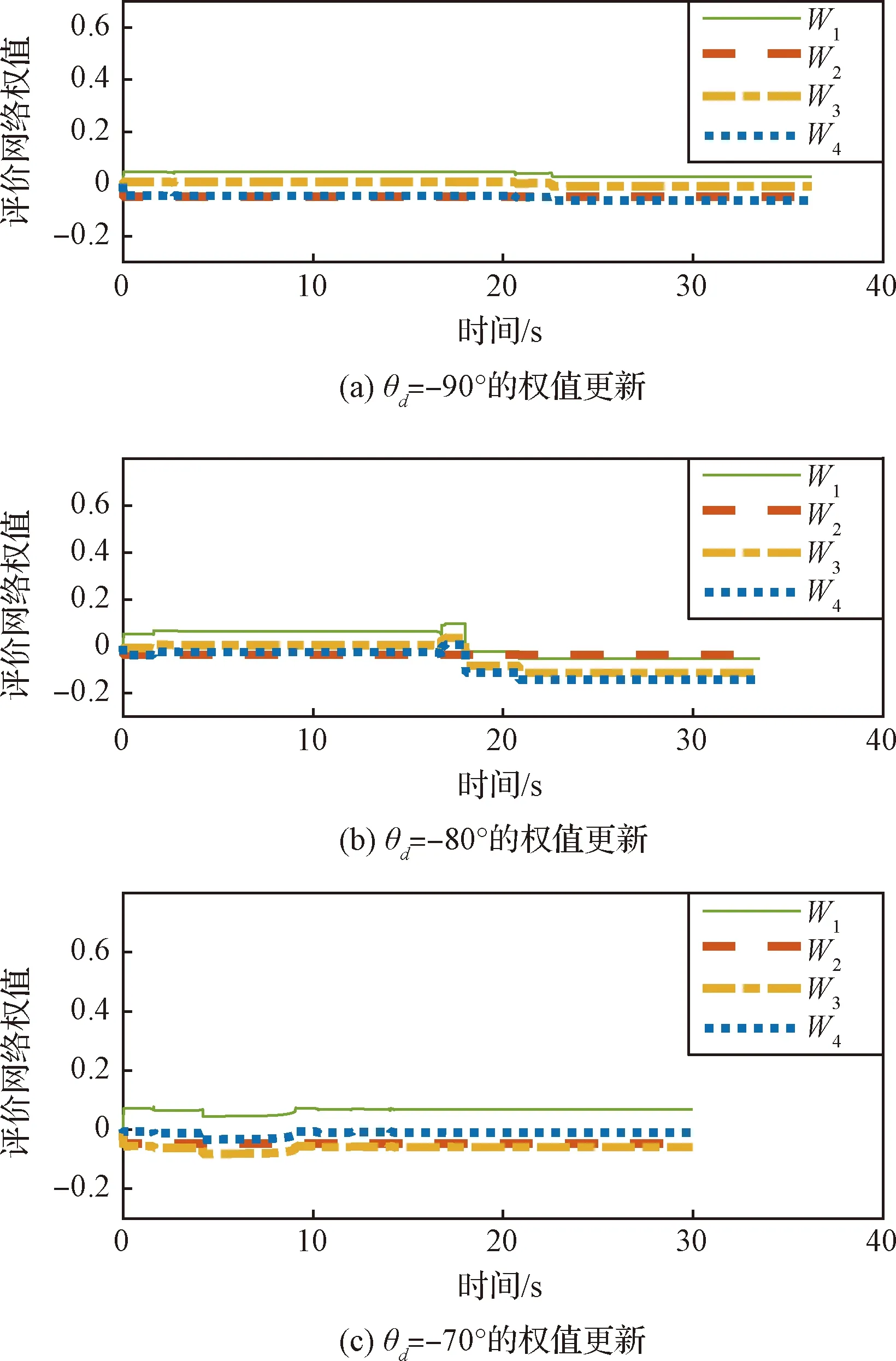
圖3 不同落角約束下，評價網絡的權值更新Fig.3 Curves of weight updating of critic network

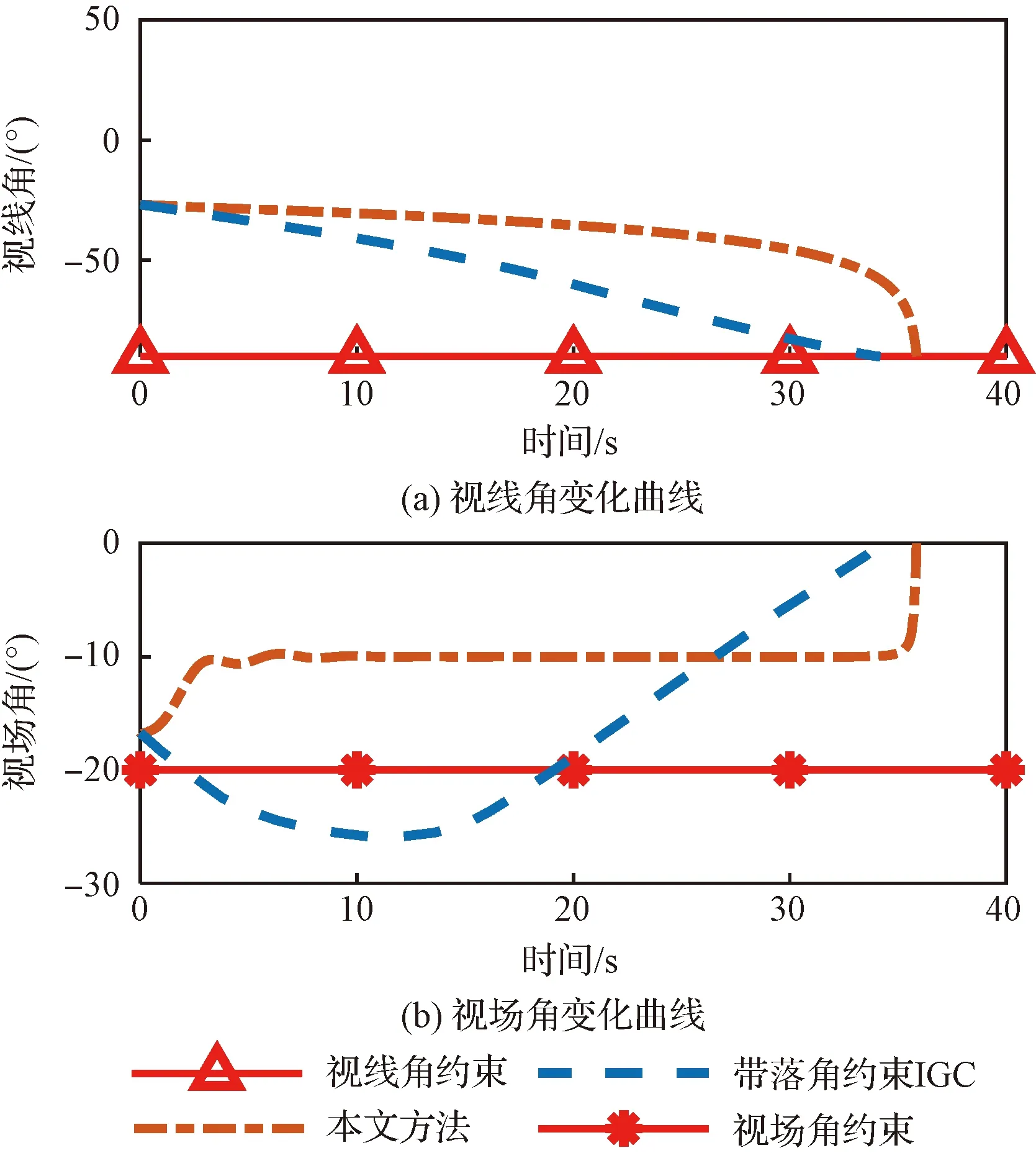
圖4 與考慮落角約束的文獻[20]方法的對比Fig.4 Comparison with the method in the reference [20] considering the impact angle constraint

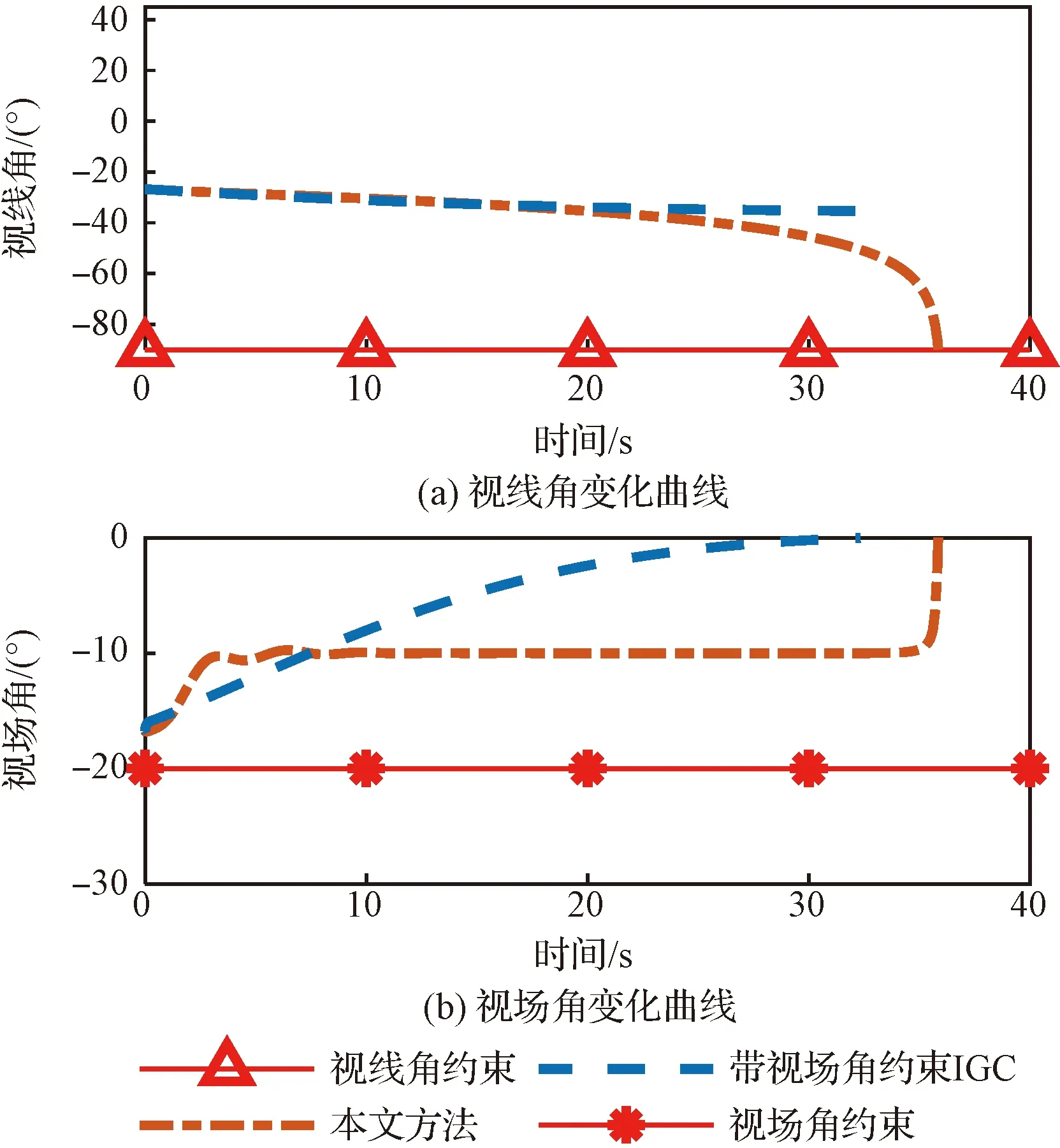
圖5 與考慮視場角約束的文獻[21]方法的對比Fig.5 Comparison with the method in the reference [21] considering the field-of-view constraint

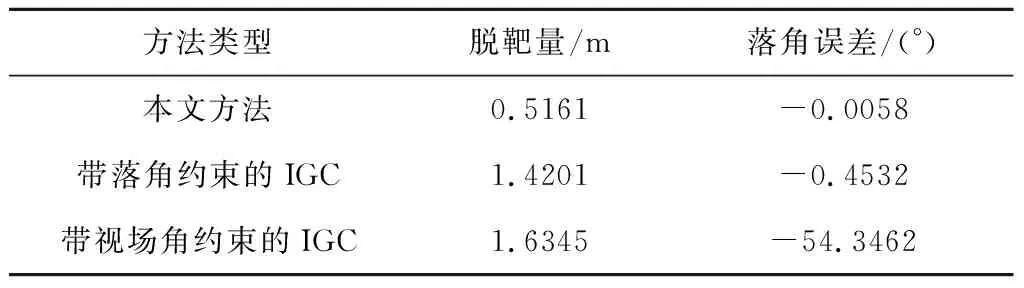
表1 結果比較Table 1 The results comparison

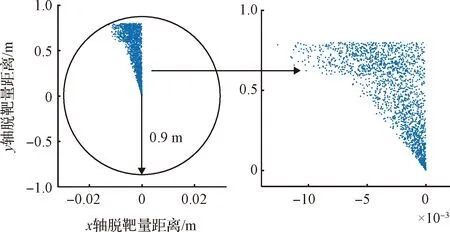
圖6 2000次蒙特卡洛仿真下的脫靶量結果Fig.6 Results of the miss distance under 2000 Monte-Carlo tests

5 結 論

本文針對考慮視場角約束和落角約束的高超聲速飛行器高精度打擊問題，提出一種基于自適應動態規劃的新型制導控制一體化策略。現有一體化方法較少同時考慮兩種約束，而本文方法將視場角約束、落角約束和命中精度要求集成到視場角指令，從而將約束問題轉化為跟蹤問題，通過自適應動態規劃的強化學習思想得到最優策略，保證在精確跟蹤的同時即可滿足這兩種約束。數學仿真驗證了提出方法的有效性及相比于現有方法的優勢。后續研究中將考慮彈道設計以及落速和時間約束，從而實現更好的打擊效果，促進高超聲速飛行器制導控制技術發展。