基于多目標粒子群算法的覆蓋件沖壓成形動態壓邊力優化
高孝書
(寧夏職業技術學院工業工程學院,寧夏 銀川 750021)
0 引言
在覆蓋件沖壓成形過程中,壓邊力是影響其成形質量的主要因素之一[1]。與傳統的恒定壓邊力相比,采用動態壓邊力能有效控制成形過程中各階段成形缺陷的產生,顯著降低開裂、起皺和回彈等缺陷對成形質量的影響[2]。通常,通過大量反復的沖壓試驗來尋找合適的恒定壓邊力是有可能的,但要想通過反復試驗獲得合適的、乃至最優的動態壓邊力是很困難的,需要借助某種優化算法才能實現[3]。
本文采用多目標粒子群優化算法,把減少開裂缺陷、起皺缺陷和回彈缺陷同時作為動態壓邊力優化目標,對全局空間進行多目標尋優,獲得全局空間解集和最優解。
1 構建動態壓邊力多目標粒子群優化模型
在覆蓋件沖壓成形中,采用動態壓邊力能更好地控制沖壓成形質量,因此構建動態壓邊力多目標優化模型的關鍵[4]。本文提出的覆蓋件沖壓成形動態壓邊力多目標粒子群優化流程如圖1 所示。
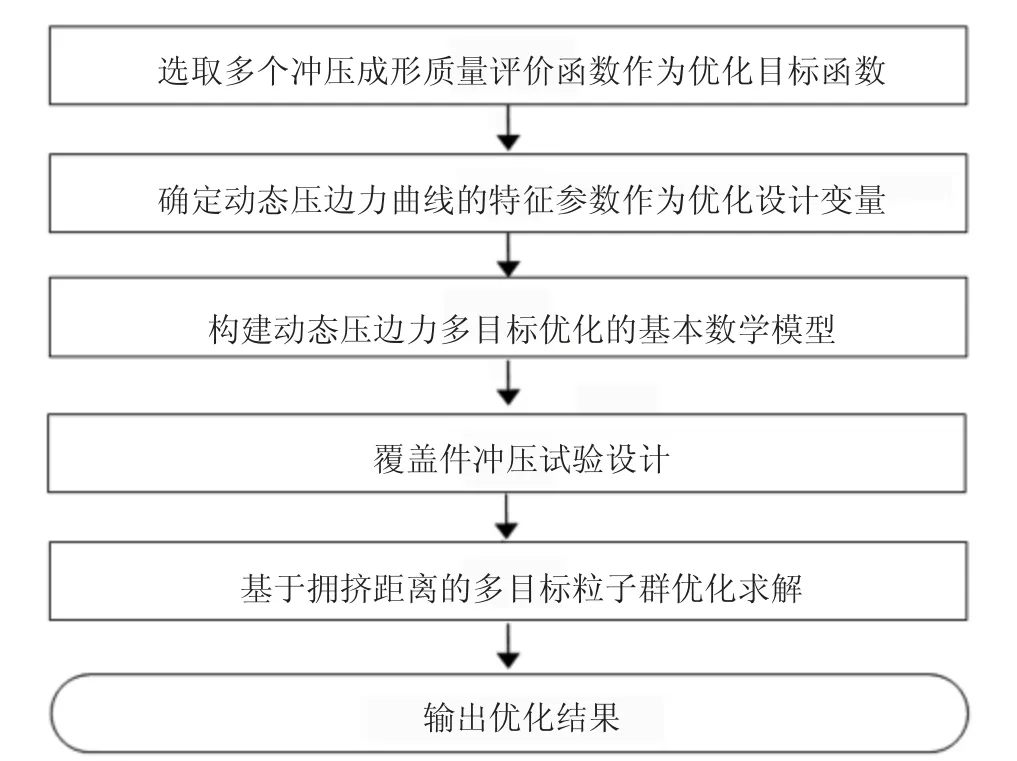
圖1 動態壓邊力多目標粒子群優化流程圖
1.1 動態壓邊力模型
覆蓋件動態壓邊力多目標優化的基本數學模型如下[5]:

式中,fi(i=1,2,…,m)為優化目標函數,分別對應開裂缺陷評價函數、起皺缺陷評價函數、回彈缺陷評價函數等,m 為優化函數總數;xj(j=1,2,…,n)為優化設計變量,分別對應動態壓邊力曲線的特征參數值,n 為特征參數總數;X 為設計變量的全局計算空間。
1.2 多目標粒子群優化算法
多目標粒子群優化算法源于鳥群搜索食物過程,個體位置的智能調整導致了群體行為的優化,由于其易實現性高,通常在大變形的沖壓成形中具有比遺傳算法更高的有效性[6]。本文以基于擁擠距離的多目標粒子群優化(Crowding distance in multi-objective particles swarm optimization,MOPSO-CD)來求解覆蓋件沖壓成形動態壓邊力優化問題,其基本算法如下:
(1)初始化粒子群POP:for i=0 to MAX//MAX為種群數量,隨機產生每個粒子的位置POP[i];
(2)初始化每個粒子的速度:VEL[i]=0;
(3)計算每個粒子所對應的目標矢量,評估每個POP 中的粒子;
(4)把粒子群中的非劣解存放到檔案REP 中;
(5)增量循環以上過程至達到最大迭代次數M,直至程序結束。
2 覆蓋件沖壓成形動態壓邊力優化實例
2.1 U 型沖壓件動態壓邊力多目標優化
U 型沖壓件是典型的沖壓成形件,其沖壓缺陷主要是開裂、起皺和回彈,采用動態壓邊力沖壓能很好地控制這3 類沖壓缺陷的產生[7]。通常,隨著壓邊力的增大,U 型沖壓件的起皺和回彈越小,但開裂的風險越大[8]。評價開裂的指標參數是最大減薄率,評價起皺的指標參數是最大增厚率,評價回彈的指標參數是法蘭邊緣處的最大垂直回彈位移,回彈前后U 型沖壓件的形狀如圖2 所示。
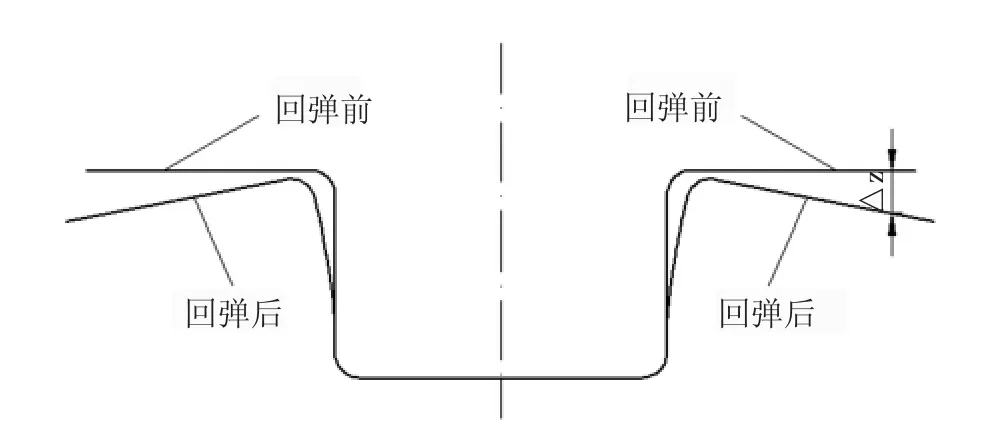
圖2 回彈前后U 型沖壓件的形狀
本文選取最大減薄率、最大增厚率、最大垂直回彈位移作為優化目標函數,使沖壓件在最小開裂、起皺和回彈的情況下,獲得充分的U 型標準成形,U 型標準模型如圖3 所示。
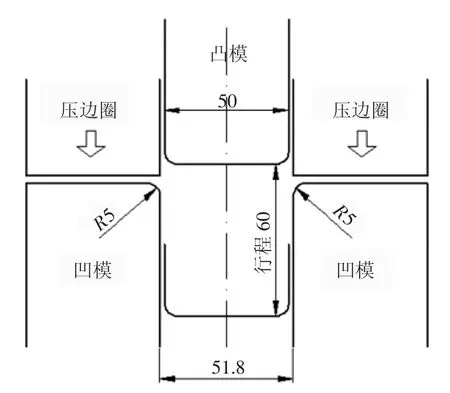
圖3 U 型標準模型
沖壓板材選用0.8mm 厚的AZ31B 鎂合金薄板,長300mm,寬30mm;凸模最大行程為60mm,沖壓速度為5mm/s,凹凸模間隙為0.9mm,板材溫度為260℃,摩擦系數為0.11;采用DYNAFORM 有限元模擬軟件,對后U 型沖壓件進行LS-DYNA 求解計算。
2.1.1 建立多目標優化模型
動態壓邊力的施加采用階梯式曲線,如圖4 所示。VBF1為小壓邊力,VBF2為大壓邊力,t1為壓邊力變化時刻,t2為沖壓結束時刻。
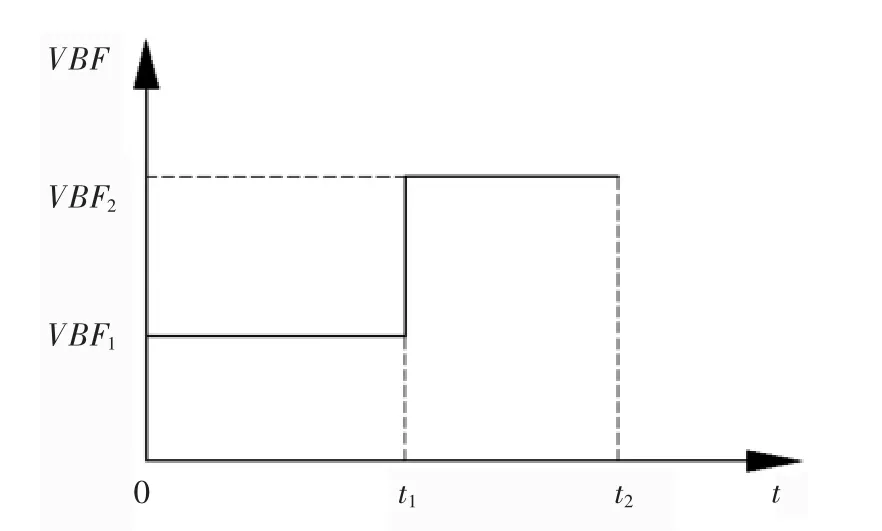
圖4 動態壓邊力階梯式曲線
將壓邊力檢測點的參數值VBF1、VBF2、t1作為多目標優化設計變量,則U 型沖壓件的動態壓邊力多目標優化問題可表述為:
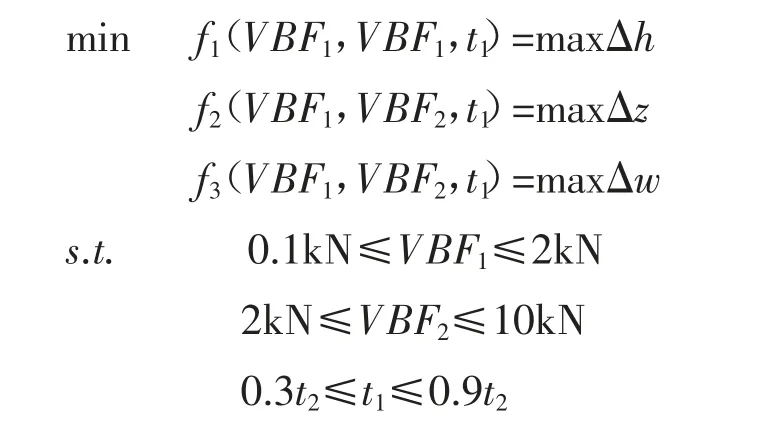
式中,maxΔh 為U 型沖壓件的最大減薄率;maxΔz 為U 型沖壓件的最大垂直回彈位移;maxΔw 為U 型沖壓件的最大增厚率。
2.1.2 計算結果分析
試驗選用種群粒子數為100,慣性權重為0.4,個體學習因子為0.5,全局學習因子為0.5,外部檔案容量為100,最大迭代次數為100。經迭代計算后,全部非劣解集在空間中的分布如圖5 所示。從圖5 可見,最大減薄率、最大增厚率、最大垂直回彈位移3 個優化目標函數相互制約,無法同時達到最小。本文利用最小距離選解法,通過計算各個粒子到原點的距離,對3 個目標函數加權平均后,從空間的所有解中選取了最優解(Pm)。
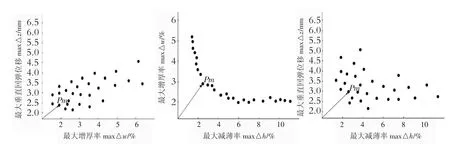
圖5 空間解及最優解(Pm)
采用最優解(Pm)對應的工藝參數,進行有限元模擬沖壓成形計算,獲得的U 型沖壓件成形極限圖(FLD)如圖6 所示。從圖6 可知,在U 型沖壓件充分成形的情況下,采用動態壓邊力能有效地控制開裂和起皺缺陷。
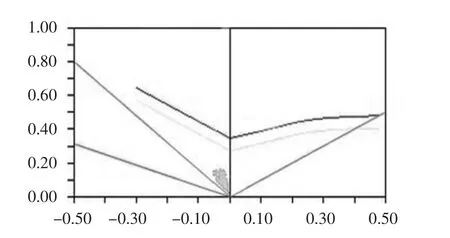
圖6 采用最優解(Pm)時的成形極限圖
2.2 方盒型沖壓件動態壓邊力多目標優化
為了進一步驗證動態壓邊力多目標優化方法解決實際問題的能力,本文以某鎂合金方盒型沖壓件為研究實例,其有限元模型如圖7 所示。
從圖7 可知,該方盒型沖壓件的回彈量較小,其最大垂直回彈位移可作為次要的常量因素考慮。影響該方盒型沖壓件成形質量的主要缺陷的開裂和起皺,對應的評價指標參數分別為最大減薄率和最大增厚率。
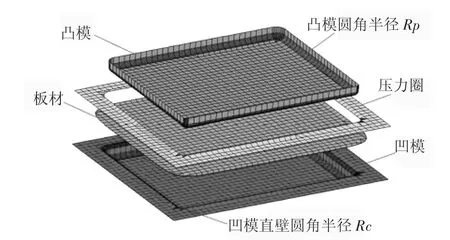
圖7 某方盒型沖壓件的有限元模型
方盒型沖壓件長400mm,寬250mm,高40mm,沖壓板材為1.0mm 厚AZ31B 鎂合金薄板,沖壓速度為1.2mm/s,凹凸模間隙為1.1mm,板材溫度為255℃,摩擦系數為0.12;采用DYNAFORM 有限元模擬軟件,對方盒型沖壓件進行有限元模擬計算。
2.2.1 建立多目標優化模型
動態壓邊力施加采用圖4 中的階梯式曲線,將壓邊力檢測點的參數值VBF1、VBF2、t1作為多目標優化設計變量,則方盒型沖壓件的動態壓邊力多目標優化問題可表述為:
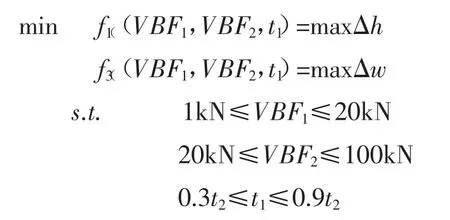
式中,maxΔh 為U 型沖壓件的最大減薄率;maxΔw 為U 型沖壓件的最大增厚率。
2.2.2 計算結果分析
試驗選用種群粒子數為100,慣性權重為0.4,個體學習因子為0.5,全局學習因子為0.5,外部檔案容量為100,最大迭代次數為100。經迭代計算后,全部非劣解集在空間中的分布如圖8 所示。利用最小距離選解法,通過計算各個粒子到原點的距離,從空間的所有解中選取了最大減薄率和最大增厚率最低的粒子,即開裂和起皺缺陷控制最好的最優解(Pm)。
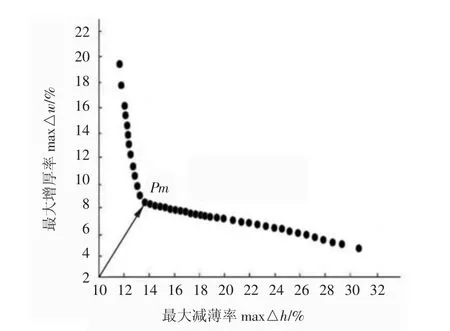
圖8 空間解及最優解(Pm)
采用最優解(Pm)對應的工藝參數,進行有限元模擬沖壓成形計算。優化前后對比結果見圖9 成形極限圖(FLD)。
從圖9a、b 的對比中可以看出,采用動態壓邊力多目標優化的方盒型沖壓件的成形效果,要顯著優于恒定壓邊力的沖壓成形效果,表明了該優化方法在解決覆蓋件沖壓成形問題時的實用性和優越性。

圖9 優化前后成形極限圖(FLD)對比結果
3 結論
本文提出基于多目標粒子群算法的覆蓋件沖壓成形動態壓邊力優化方法,把開裂、起皺和回彈同時作為壓邊力優化目標,以動態壓邊力曲線的特征參數為優化變量,采用基于擁擠距離的多目標粒子群優化算法(MOPSO-CD)和最小距離求解法,對U 型沖壓標準模型和某方盒形覆蓋件分別進行了動態壓邊力優化試驗。結果表明,該方法能快速得出最優化的動態壓邊力施加方案,有效解決U 型沖壓件和方盒形覆蓋件的開裂、起皺和回彈缺陷,具有較強的工程實用性。

