土-結構群相互作用體系地震響應振動臺試驗研究1

王國波 王 垚 王建寧 董正方

1）溫州大學, 建筑工程學院, 浙江溫州 325035

2）中國機械工業集團有限公司, 北京 100080

3）河南大學, 土木建筑學院, 河南開封 475004

引言

隨著城市化進程的加快，各種地表建筑密集出現，城鎮建筑布局與建筑形式日益復雜，同時面臨著嚴重的地震災害威脅。當地震來臨時，由于建筑物的間距越來越小，尤其是位于軟土上的結構群，難以避免地與下部地基土發生相互作用及動力耦合，并進一步影響結構群的地震響應，土與密集的地表結構群構成了復雜的土-結構群相互作用（Soil-Structure Cluster Interaction，SSCI）體系，同時土-結構群相互作用體系還包含土-結構相互作用（Soil-Structure Interaction，SSI）體系及結構-土-結構相互作用（Structure-Soil-Structure Interaction，SSSI）體系等子體系。地震測量儀器不能安裝在樹附近，以避免出現較大的測量誤差，這是由于地震時樹的晃動會影響周圍土體，從而影響測量儀器的工作，即考慮了SSI 的影響（Anand 等，2018）。然而，現行結構抗震設計規范均將地基假設為剛性的，認為結構在地面運動作用下的響應與周圍結構無關，忽略了SSI、SSCI 對結構地震響應的影響，這種假設在多數情況下是合理的，但對于間距較小的密集結構群而言有待商榷，現有研究表明位于軟土層上的建筑群會顯著改變其周圍地表的運動（Bard 等，2008）。

由于實際的城市建筑群往往規模巨大，因此數值分析是研究SSCI 的主要手段，目前關于SSCI 研究的常用數值方法有有限單元法（FEM）、有限差分法（FDM）、邊界單元法（BEM）、有限元-邊界單元耦合法（BEM-FEM）、譜單元法（SEM）等。Isbiliroglu 等（2015）建立相應的三維有限元模型，對地震作用下單個建筑及理想建筑群與土體的相互作用效應進行研究，并結合域縮減法模擬地震動激勵，結果表明SSCI 與建筑物數量、動力特性、間距及相對于土體的阻抗有關。Li 等（2020）利用Ls-dyna 軟件建立了地表結構群-土-地下結構的大型有限元模型，并通過時域和頻域的三維完全耦合動力分析，強調了地上建筑物對地下結構的影響，結果表明，地上建筑物的存在通常會降低車站響應，且可增加或減少地鐵隧道響應。Long 等（2021）建立了一系列不同建筑物間距的建筑場地二維有限元分析模型，采用靜動力耦合數值模擬方法研究了不同地震動作用下的SSSI。Aji 等（2022）采用BEM-FEM 評估了位于彈性層狀半無限空間上2 個相鄰結構的動力響應，結果表明SSSI 體系的動力響應取決于遠場地質帶的任意分層、動力源特征、場地效應現象、基礎和結構類型和幾何配置等因素。Kumar 等（2018，2019）采用FDM 對建筑物和場地共振條件下二維與三維模型的SCI 進行研究，結果表明SCI 會導致結構共振頻率的顯著降低。 Ayala 等（2022）提出了SEM 與Galerkin 法相結合的數值方法，并建立了妮維雅德爾瑪市三維地震傳播模型，以評估場地-城市動力相互作用在城市環境中的貢獻，并在后續研究中基于該數值方法評估了SSI 對帶地下室剪力墻結構的影響。巴振寧等（2022）采用 Specfem 3D 開源程序，通過建立含直下型垂直走滑斷層動力學震源和三維沉積盆地的整體物理模型，研究了直下型垂直走滑斷層動力學震源作用下的三維沉積盆地地震動基本特征和不同斷層面初始剪應力及不同成核區位置下三維沉積盆地地表響應規律。

數值模擬方法的發展雖為SSCI 研究提供了極大便利，但基于振動臺的物理模型試驗仍是不可替代的。Wang 等（2022b，2022c）開展了SSI 與SSCI 振動臺試驗，并進行數值模擬分析與參數分析，結果表明與SSI 相比，SSCI 對上部結構頂部加速度的影響范圍為?40%～27%。SSCI 對于軟土來說是顯著的，且隨著結構數量的增加和結構間距的減小而增大。此外，SSCI 可改變地面加速度響應譜，顯著改變結構加速度響應的最大傅里葉幅值。Aldaikh 等（2015，2016）進行了一系列振動臺試驗，研究SSSI 對與2 個以上相鄰建筑模型動力響應的影響，結果表明與單個結構相比，2 個相鄰建筑物的存在可能對建筑物地震功率和峰值加速度響應產生積極或消極的影響，具體取決于其高度。Ge 等（2019）通過振動臺試驗研究了土-高層建筑群的動力相互作用，高層建筑在試驗中被簡化為混凝土柱，結果表明SSCI 可降低結構加速度響應，而建筑數量是SSCI 最顯著的影響因素，且SSCI 隨著結構間距的增加逐漸減小。

在現有的大多數振動臺試驗中，建筑物往往被簡化為單自由度集中質量模型或混凝土塊之類的簡化結構，雖可較準確地評估SSCI 對結構加速度響應的影響，但難以反映真實工程結構在SSCI 影響下的響應特點。已有研究表明當地表結構數量達5 個時，可在一定程度上考慮其群體效應（Schwan 等，2016），為此本文設計并制作5 個縮尺框架結構模型，進行一系列土-結構（群）體系振動臺試驗，探究結構數量、地震動類型與幅值對SSCI 的影響，同時兼顧結構（群）對土體響應的影響。

1 振動臺試驗設計

1.1 模型箱

本試驗在北京工業大學工程結構實驗室的9 子臺上進行，振動臺為4 個1 m×1 m 臺面組成的臺陣。模型箱由2 個主動箱和1 個從動箱組成，主動箱固定在振動臺臺面上，從動箱位于中間，通過鋼梁及懸掛裝置與兩側的主動箱連接，如圖1 所示。本試驗同時考慮了一致與非一致地震動輸入，本文僅分析一致輸入時結構群地震響應規律，此時將3 個箱體通過螺栓和底部鋼板連為一體，使其成為整體剛性箱。模型箱內部四周放置0.15 m 厚泡沫板，以降低波在界面的反射，土體尺寸為3.5 m×2.5 m×1 m。

圖1 模型箱Fig. 1 Model box

1.2 相似關系

根據Bukingham 定理，以長度、彈性模量、加速度為基本物理量，根據相似條件間的關系可初步確定其他相似關系。首先，根據振動臺與模型箱尺寸確定長度相似關系為1/30；然后，采用微粒混凝土制作結構模型，本試驗進行了不同配合比下的微粒混凝土彈性模量測試（Wang 等，2022a），最終確定微粒混凝土質量比為：水泥∶細料∶粗料∶減水劑∶水=1∶2.5∶2.5∶0.014∶0.686，測得其軸心抗壓強度為17 MPa，彈性模量約為15 GPa，密度為2 333 kg/m3，常規C40 混凝土彈性模量為32.5 GPa，則彈性模量相似比為0.462；最后，依據振動臺性能將加速度相似比取為2。模型體系各物理量的相似系數及相似關系如表1 所示。

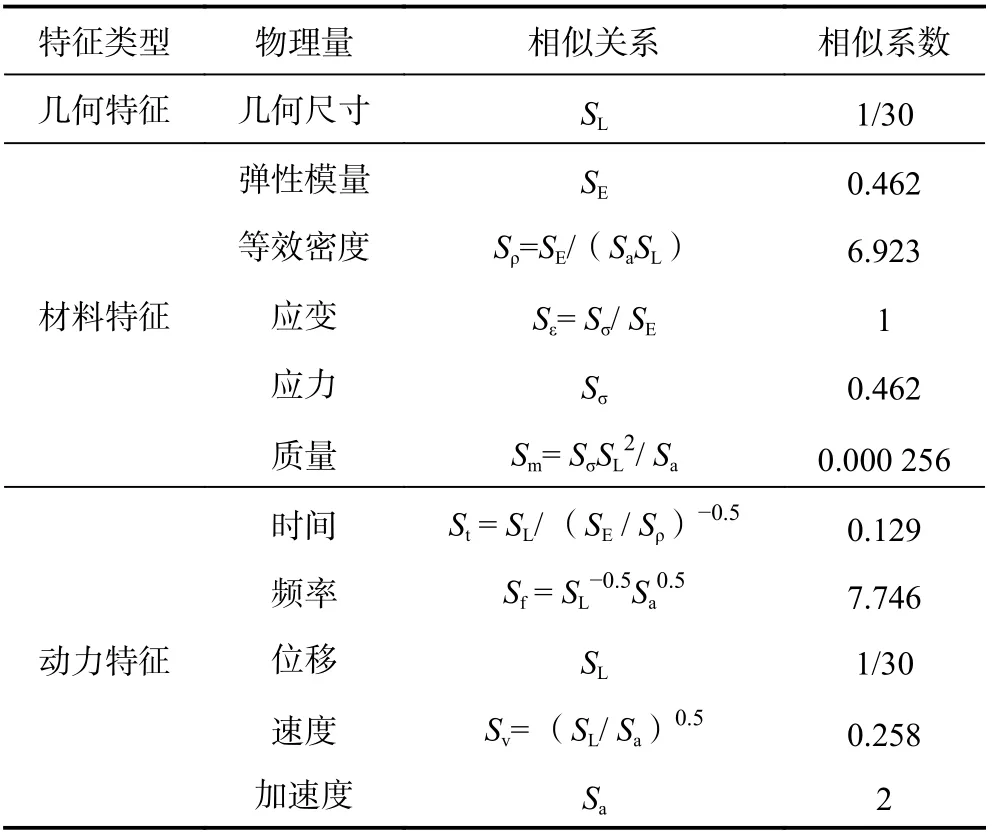
表1 相似系數與相似關系Table 1 Similarity coefficient and similarity relation

1.3 模型結構

本試驗原型為采用筏板基礎的框架結構，縱、橫向跨度均為6 m，層高3 m，層數為6，其中柱和梁截面尺寸分別為 0.4 m×0.4 m 和 0.6 m×0.3 m，樓板厚0.12 m，筏板長、寬均為7.2 m，厚0.75 m。根據幾何相似比可確定模型結構尺寸。梁、板、柱等構件縱筋及箍筋采用鍍鋅鐵絲模擬。模型結構設計與制作如圖2所示。

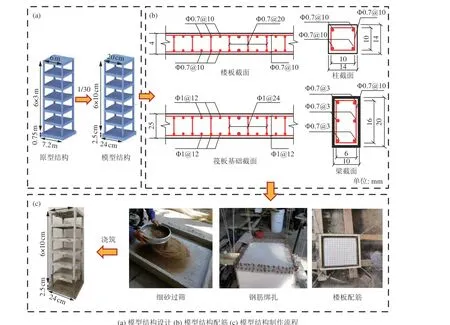
圖2 模型結構設計與制作示意Fig. 2 Model structure design and schematic diagram

由于慣性力對地表結構起控制作用，因此需對結構進行配重設計。計算模型配重時，首先由原型結構質量按相似常數計算得到模型理論所需質量，然后減去模型自重產生的質量，即可得到模型對應樓層所需配重。經計算共需配重47.25 kg，平均每層樓板配重7.875 kg，每層采用2 塊尺寸為24 cm×13 cm×1.6 cm（長×寬×高）的鐵板，質量約7.8 kg。

1.4 模型土

本試驗采用北京某地鐵站場地淤泥質黏土作為模型土，首先去除雜質和粒徑較大的土顆粒，然后將土分層倒入模型箱內壓實，每層厚10 cm，共厚100 cm。每層土壓實后利用環刀采集土壤，測得箱內土壤平均密度為1 850 kg/m3。為進一步了解模型土動力特性，利用共振柱試驗得到模型土動剪切模量和動阻尼比，并通過Hardin-Drnevich 公式（Hardin 等，1972）進行擬合：

式中，G與Gmax分別為動剪切模量與最大剪切模量；D與Dmax分別為動阻尼比與最大阻尼比； γ 與 γr分別為動剪應變與參考剪應變。

圖3 為模型土歸一化動剪切模量衰減曲線及動阻尼比變化曲線，由圖3 可知，模型土動剪切模量隨著動剪應變的增大而減小，而動阻尼比隨著動剪應變的增大而增大，表明本研究選取的北京地區粉質黏土符合軟土在地震作用下的應變軟化規律。

圖3 共振柱試驗結果與擬合曲線Fig. 3 Resonant column test results and fitting curves

1.5 結構布置與監測

試驗體系測點布置如圖4 所示，x向為水平縱向，y向為水平橫向，z向為豎向。首先在振動臺臺面布置加速度傳感器T1～T3，監測臺面加速度響應，作為后續數值計算的輸入地震動。沿地表縱向，間隔0.25 m布置加速度傳感器A1～A9，監測場地土加速度響應。在結構1～5 基礎、地上3 層及頂部布置加速度傳感器J1～J15，監測結構加速度響應，同時布置激光位移計D1～D5，監測各結構頂部在激勵方向的位移。

圖4 土-結構群試驗體系測點布置示意Fig. 4 Monitor layout of soil-structure cluster test systems

1.6 加載工況

本試驗輸入的波主要包括用于掃描的白噪聲（用WN 表示）、經典El Centro 波（用EL 波表示）、脈沖波Northridge 波（用NR 波表示）、取土地區的北京人工波（用BJ 波表示）和用于檢驗模型箱邊界效應的正弦波。邊界效應參見Wang 等（2022a）的研究，未將正弦波列入加載工況（表2）。EL 波、NR波和BJ 波按照時間相似比壓縮后的加速度時程曲線與傅里葉譜如圖5 所示。

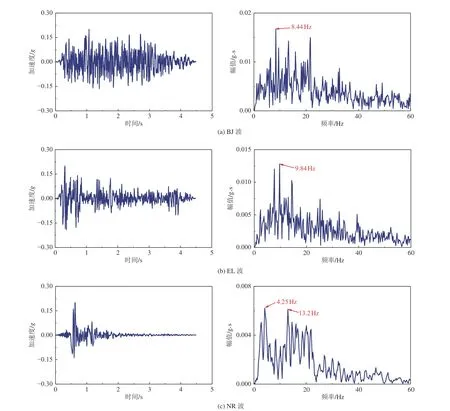
圖5 輸入地震波時程及頻譜曲線Fig. 5 Time histories and Fourier spectrums of the input seismic wave

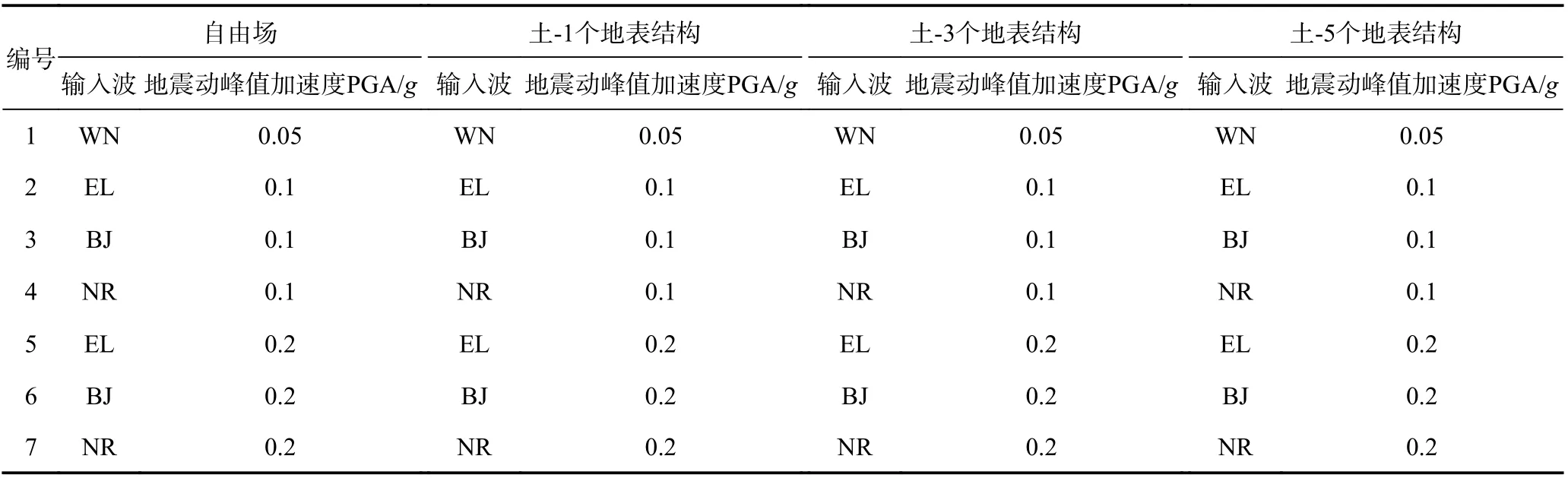
表2 加載工況Table 2 Test loading cases

2 振動臺試驗結果分析

本試驗包含自由場、土-1 個地表結構、土-3 個地表結構和土-5 個地表結構體系，分別用FF、SS1、SS3、SS5 表示。

2.1 土體響應

從峰值加速度與能量角度分析SSCI 對中心結構基礎底部土體的影響，能量采用Arias Intensity 指標Ia表示（Barrios 等，2021），可按下式計算：

式中，a（t）為加速度，t為補充時間，T為補充加速度的持續時間，g為重力加速度。

以自由場工況為基準，按下列公式評價地表結構對場地土的影響程度：

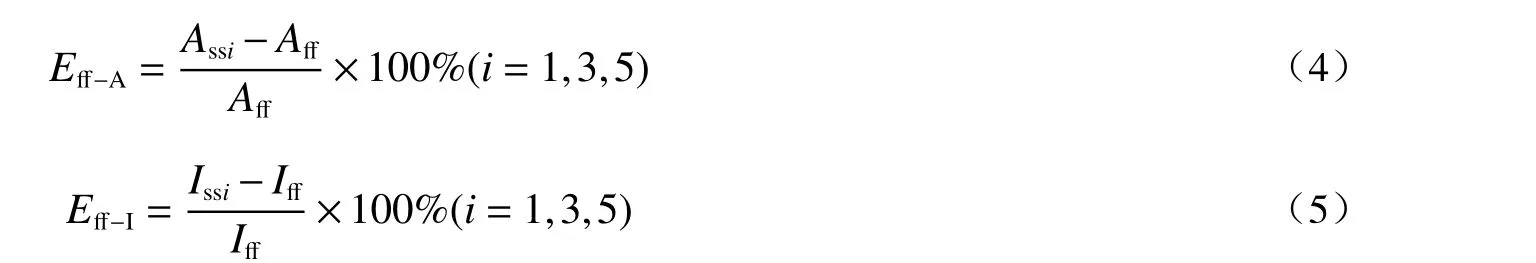
式中，Eff-A為測點A5 的加速度變化百分比，Aff、Ass1、Ass3、Ass5分別為自由場、SS1 體系、SS3 體系、SS5體系測點A5 的加速度幅值，Eff-I為測點A5 的Ia變化百分比，Iff、Iss1、Iss3、Iss5分別為自由場、SS1 體系、SS3 體系、SS5 體系內測點A5 的Ia值。

不同工況下峰值加速度變化率及Ia指標對比結果如圖6、圖7 所示。

圖6 不同地震動激勵下測點A5 的峰值加速度對比Fig. 6 Comparison of the peak acceleration at the A5 under different seismic excitations

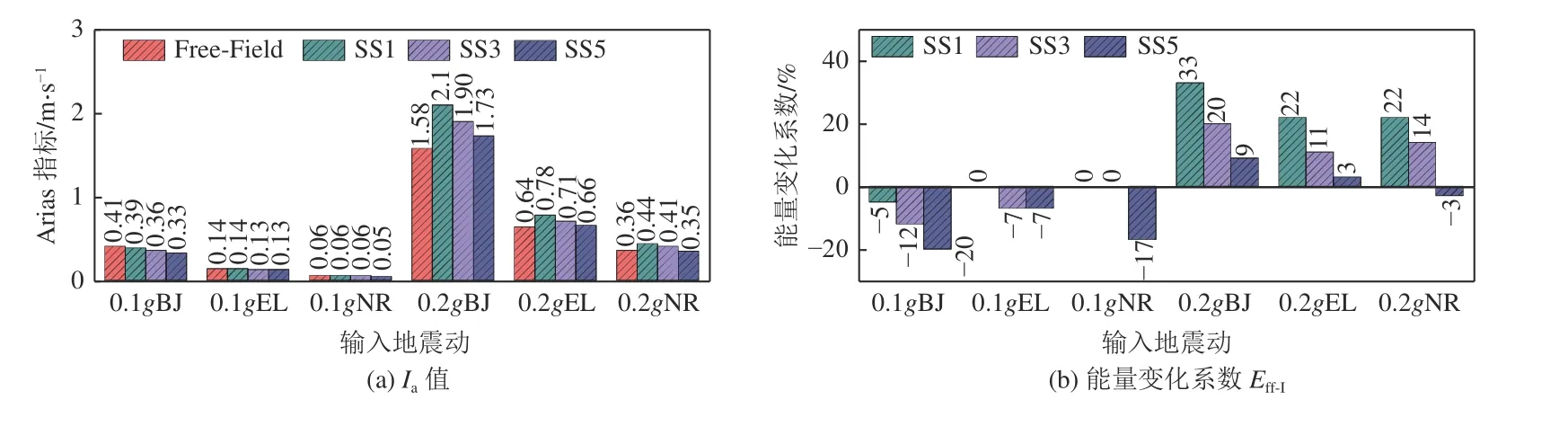
圖7 不同地震動激勵下測點A5 的Ia 值對比Fig. 7 Comparison of the Arias intensity at the A5 under different seismic excitations

由圖6、圖7 可得以下結論：

（1）地表結構數量的影響：土體加速度響應隨著結構數量的增加而減小，且當結構數量由3 個增至5 個時，變化率顯著降低，體現了群體效應的影響。

（2）地震動類型的影響：BJ 波激勵下，結構數量變化對場地土響應的影響最顯著，NR 波其次，EL波的影響較小，這是因為由輸入地震動Ia值可知BJ波總能量遠高于NR 波與EL 波（圖8），因此BJ 波激勵下土體響應最強烈，SSCI 對土體的影響最顯著，且模型土基頻約為12.8 Hz（Wang 等，2022a），該頻率與NR 波主頻13.2 Hz 最接近，且遠離EL 波主頻9.84 Hz，因此，NR 波能量水平雖低于EL 波，但NR波激勵下SSCI 對土體的影響較EL 波激勵下更顯著。

圖8 輸入地震動Ia 值Fig. 8 Arias intensity of input seismic waves

（3）地震動幅值的影響：當地震動幅值較小（0.1g）時，地表結構的存在以抑制土體加速度為主，而當地震動幅值較大（0.2g）時，地表結構以放大土體加速度為主，這是因為當地震動幅值較小時，地表結構作為1 個質量塊抑制了土體運動，這與已有研究在地表放置質量塊達到減振的原理類似（Dijckmans 等，2015），但隨著地震動幅值的增加，土體非線性變形增加，土體對結構的約束降低，結構加速度增加，慣性力增加，從而放大了土體響應。

（4）Ia指標變化規律最大差異體現在EL 波上，能量指標綜合考慮了整個時程的累積效應，此時卓越頻率的影響不再顯著。由此可見，采用不同的評價指標可在整體上得到類似的規律，但在細節上仍存在差異，體現了不同指標之間的側重點不同。

測點A5 加速度響應譜如圖9 所示，由圖9 可知，結構的出現放大了土體響應譜幅值，然而隨著結構數量的增加，土體響應譜幅值仍表現出逐漸減小的趨勢，由此可見SSCI 會減小土體響應，其主要原因在于在輸入地震動能量相同的情況下，地表結構數量的增加會分擔一定的地震動能量，從而降低土體響應。另外，結構數量的增加導致了土體卓越周期略微放大，這是由于試驗連續加載導致土體剛度發生退化。

圖9 不同地震動激勵下測點A5 的加速度響應譜Fig. 9 Acceleration spectrums of A5 under different excitations

2.2 結構加速度

定義峰值加速度變化系數Ea，以評估結構數量增加對中心結構頂層樓板加速度響應的影響：

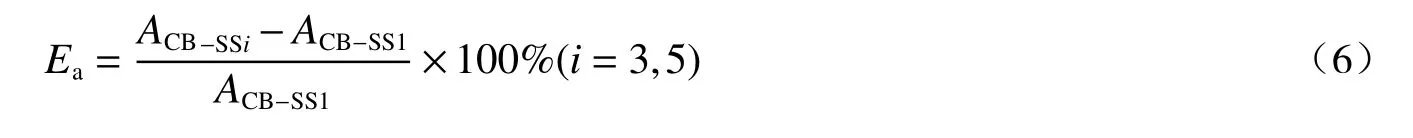
式中，ACB-SS1、ACB-SS3和ACB-SS5分別表示SS1、SS3 和SS5 體系中心結構頂層樓板加速度幅值。

中心結構頂部加速度峰值及變化系數Ea如圖10 所示，不同地震動激勵下結構頂層樓板加速度響應的頻譜曲線（綠色線為結構響應的主頻）如圖11 所示，由圖10、圖11 可得以下結論：

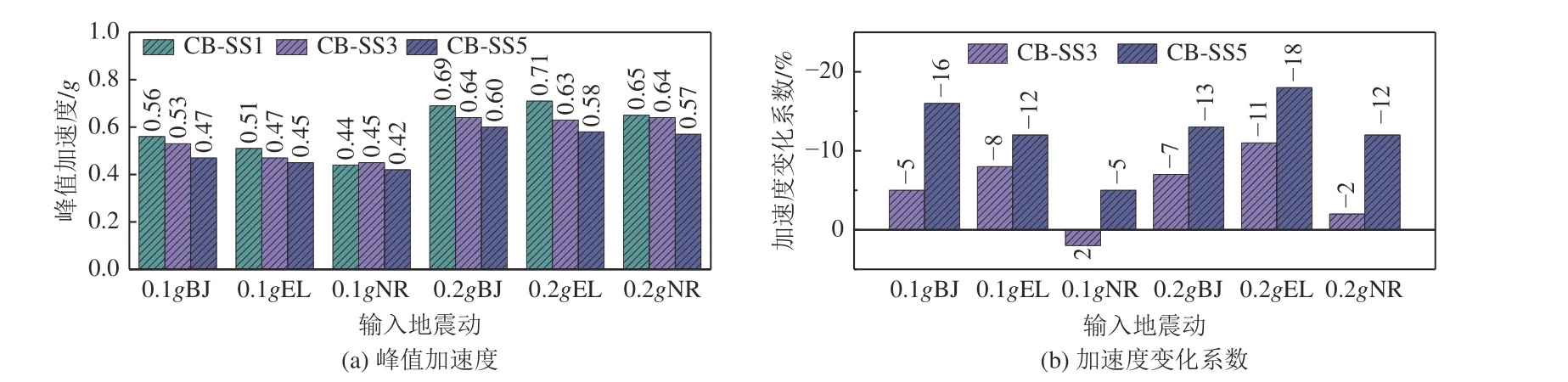
圖10 中心結構頂部峰值加速度對比Fig. 10 Comparison of the peak acceleration at the roof of central buildings under different excitations

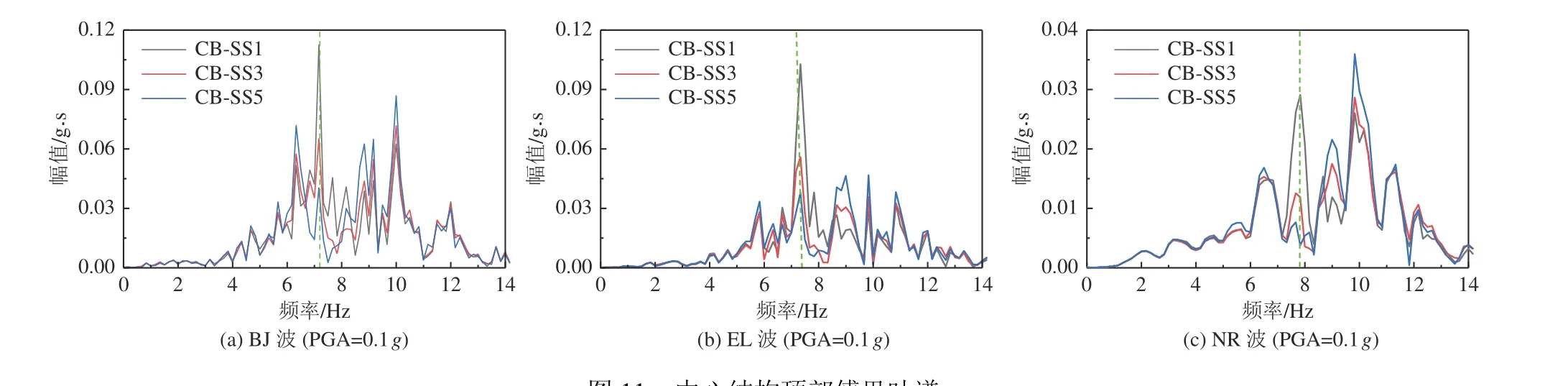
圖11 中心結構頂部傅里葉譜Fig. 11 Fourier spectrums of the central building roof

（1）中心結構頂層樓板加速度表現出隨著結構數量的增加逐漸減小的趨勢，且當結構數量由3 個增至5 個時，其降低趨勢更顯著，體現了群體效應。以BJ 波為例，當結構數量由1 個增至3 個時，結構頂部加速度減小幅度為5%，而當結構數量進一步增至5 個時，減小幅度達16%，這是因為同一地震動輸入給體系的總能量一定，結構數量越多，每個結構分擔的能量越少，因而結構加速度響應隨著結構數量的增加而降低。總體而言，SSCI 效應最大可降低18%的結構頂部加速度響應。

（2）地震動幅值的影響并不顯著，但地震動類型的影響差異較大。開展敲擊試驗，通過自由振動衰減曲線可得3 個結構基頻均為7.2 Hz，NR 波主頻4.5、13.2 Hz 遠離結構基頻，而BJ 波和EL 波主頻8.44、9.84 Hz 與結構基頻較接近，因此響應較大，體現了地震動頻率特性的影響。

（3）結構響應的能量主要集中在5～12 Hz，需注意的是，結構數量的增加顯著減低了結構基頻附近7～8 Hz 帶寬內的傅里葉幅值，但顯著放大了模型土卓越頻率（12.8 Hz）附近8～11 Hz 帶寬內的傅里葉幅值，體現了場地土對結構體系地震響應的影響。

2.3 結構位移

對于框架結構而言，層間位移角是衡量其抗震性能的關鍵指標。但本試驗僅監測了結構頂層沿激勵方向的位移，無法得到層間位移，因此僅分析結構頂層的絕對位移。定義結構峰值位移變化系數Ed，評價相鄰結構對中心結構位移幅值的影響：

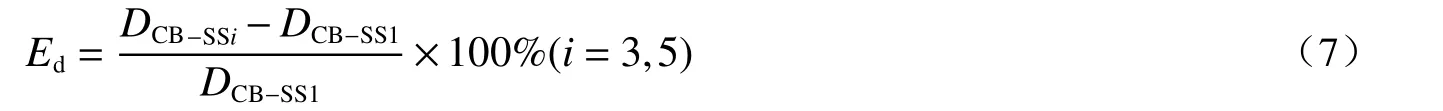
式中，DCB-SS1、DCB-SS3和DCB-SS5分別為SS1、SS3 和SS5 體系中心結構頂層樓板沿激勵方向的位移。

各體系中心結構頂部位移時程曲線如圖12 所示，結構頂層峰值位移及變化系數Ed如圖13 所示。由圖12、圖13 可得以下結論：

圖12 中心結構頂部的位移時程曲線Fig. 12 Displacement time histories of the central building roof

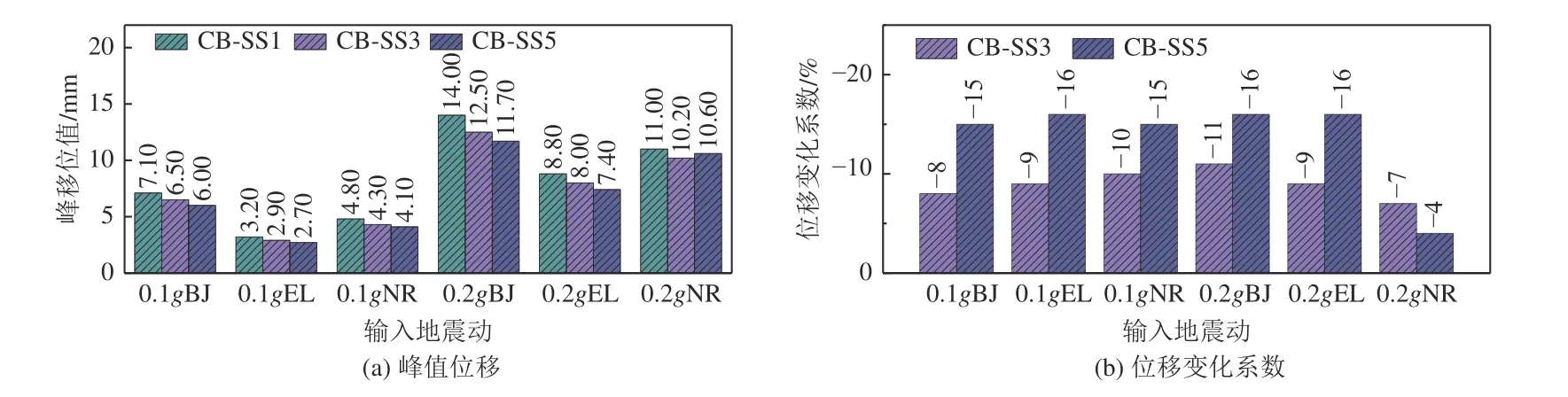
圖13 中心結構頂部的峰值位移對比Fig. 13 Comparison of peak displacements of the central building roof

（1）各體系內中心結構頂部位移曲線變化趨勢基本保持一致。

（2）中心結構頂部位移表現出隨著結構數量的增加而減小的趨勢，體現了群體效應的影響，并且SSCI效應最大可降低16%的中心結構頂部位移響應。

（3）不同地震動幅值下各體系中心結構位移峰值變化系數變化較小，表明結構位移響應對地震動幅值并不敏感。

（4）對于地震動類型而言，BJ 波作用下結構位移最大，其次是NR 波，EL 波最小，這與上述分析的加速度規律一致。

（5）NR 波作用下結構位移呈典型的脈沖特性，即僅有1 個脈沖的位移峰值，然后位移急劇降低并穩定在平衡位置附近，體現了脈沖波的特性。

3 結論

本文設計并開展了一系列振動臺試驗，以研究土與結構群相互作用對結構及場地土響應的影響，主要得出以下結論：

（1）結構的出現并不總是降低自由場的地面運動，結構的慣性運動可能放大其底部地基土的響應，這與輸入地震動類型及幅值密切相關，但土體響應總是隨著結構數量的增加逐漸減小。

（2）SSCI 顯著與否主要取決于結構數量，SSCI 最大可降低18%的中心結構頂部加速度及16%的位移響應。

（3）SSCI 會改變體系內波場的分布，并放大中心結構頂部響應頻譜中土體的成分。

因振動臺試驗規模有限，本試驗僅考慮了結構數量、地震動類型與幅值的影響，而結構高度、場地類型、結構間距、結構嵌入深度（基礎類型）等關鍵參數未涉及。今后將對本試驗進行數值模擬分析，在驗證數值方法的基礎上進行實際規模的場地-城市效應數值模擬，進行更精細的參數分析。