茶油摻偽定性鑒別模型的對比分析

孫婷婷，鐘瑾璟，劉劍波，任佳麗，鐘海雁，周 波

(林產可食資源安全與加工利用湖南省重點實驗室1，長沙 410004) (中南林業科技大學食品科學與工程學院2，長沙 410004) (岳陽市質量計量檢驗檢測中心食品檢驗所3，岳陽 414000) (海普諾凱營養品有限公司4，長沙 410004)

目前準確快速鑒別食用植物油摻偽的研究大部分是首先利用先進的實驗儀器和檢測技術獲得大量復雜的結構化量測數據，然后采用各種數學方法從數據中挖掘和提取出摻偽鑒別所需的特征信息[1]。目前使用較為廣泛的檢測技術和方法包括常規理化檢測法[2]、色譜法[3,4]、核磁共振法[5]、近紅外光譜法[6,7]、拉曼光譜法[8]、熒光光譜法[9,10]、電子鼻技術[11]及穩定同位素比質譜法[12]等，常規理化檢測法獲取數據較為簡單，但數據在摻偽后特征變化不明顯，使摻偽鑒別具有一定局限性；近紅外光譜法具有獲取數據簡單便捷、沒有污染、對樣品不易破壞等優點，但當樣品量較小時，效果相對不佳；核磁共振和穩定同位素比質譜等大型儀器設備操作復雜繁瑣，無法滿足市場快速檢測的需求；電子鼻技術獲得的數據不穩定；而色譜法具有靈敏度高、選擇性強、分析速度快、操作簡便、樣品用量少等優勢，是目前廣泛應用在植物油摻偽鑒別中的量測數據獲得方法。

基于先進和成熟的檢測技術和方法獲得大量復雜的結構化量測數據后，根據鑒別需求和問題性質，需要采用不同的機器學習算法來挖掘和提取出摻偽鑒別所需的特征信息。食品的摻偽鑒別問題分為兩類，分別是定性摻偽鑒別和定量摻偽預測，二者分別屬于分類問題和回歸問題。目前用于食品摻偽量預測的機器學習算法主要包括人工神經網絡(ANN)[13-17]、偏最小二乘回歸(PLSR)[18-20]、多元線性回歸(MLR)[21]等。ANN對摻偽量的預測準確率高，低摻樣本預測能力強，但訓練操作耗時且復雜，計算復雜度較高，模型可解釋性差，訓練所需數據規模大；PLSR模型綜合考慮了多種特征性物質與摻偽含量的映射關系，但其只能擬合線性相關關系，摻偽量數值與作為特征物質的含量值間非線性因素增強會影響鑒別結果；MLR模型可以擬合摻偽量值與摻偽油脂的多個特征性變量之間的線性相關關系，模型原理簡單易于理解，但當變量之間存在非線性相關性時模型的適用性較差，并且當自變量個數較多時計算較為復雜[22]。此外，摻偽鑒別方法的準確率不僅取決于所采用的機器學習算法，在很大程度上還受到實驗樣本數據的影響，如當實驗樣本的覆蓋性較弱時，訓練集無法充分反映摻偽樣本的全部特征，在此基礎上訓練得到的不同機器學習算法模型的鑒別準確性就會受到影響，無法對訓練集未覆蓋的樣本做出準確的摻偽鑒別，同時在沒有充分訓練實驗樣本的前提下，訓練得到的機器學習模型對于新出現的新品種油脂(化合物組成種類和含量不同)的檢測精度受到影響[22]。

茶油是來源于山茶科(Theaceae)山茶屬(Camellia)的植物種子制備而成的一種營養豐富的食用植物油脂，主要生產地在湖南、江西、浙江、廣西和貴州等地，與橄欖油、棕櫚油和椰子油并列世界四大木本油脂[23]。茶油的營養功能價值和商品價格要高于其他食用植物油脂，導致市場上用低質低價食用植物油摻偽茶油的現象較普遍[24]，嚴重損害了茶油生產者和消費者的利益，所以建立快速、精準的檢測技術和方法來鑒別茶油摻偽是保障我國茶油生產和銷售市場正常秩序以及實現茶油高質量發展的必然需求。本研究基于脂肪酸和甘油三酯的色譜數據，運用Python語言建立并對比分析偏最小二乘回歸模型和多元線性回歸模型應用于摻偽茶油摻偽量的定量預測效果，以期為鑒別摻偽茶油純度及定量分析調和茶油配比提供參考。

1 材料與方法

1.1 實驗材料

1.1.1 主要試劑及儀器

脂肪酸甲酯標準品(FAMEs)、色譜純乙腈和色譜純異丙醇、甘油三酯標準品。

BSA124S電子分析天平(0.000 1 g)，GC 2014氣相色譜儀，VORTEX-5渦旋混勻儀，LC-20AD高效液相色譜儀(配備有CMB-20A控制器，LC-20AD二元泵，SIL-20A自動進樣器和CTO-10AS柱溫箱，蒸發光散射檢測器-2000ES)，ZORBAX SB-C18色譜柱(4.6 mm×250 mm；5 μm)。

1.1.2 茶油及其他摻偽植物油脂肪酸和甘油三酯

茶油及其他摻偽植物油脂肪酸和甘油三酯的實驗數據是基于本實驗室已報道的研究[25,26]。

1.2 摻偽茶油樣本的設計

設計茶油 (n=53) 中分別摻入米糠油、玉米油、棕櫚油、葵花籽油、大豆油、花生油、棉籽油及葡萄籽油的摻偽模型，設計2個摻偽梯度，自定為高摻偽梯度(10%、15%、20%、40%、60%、80%)和低摻偽梯度(2%、4%、6%、8%、10%)。高和低摻偽茶油樣本數據量為318條和265條。各摻偽濃度均含53條數據，每條數據包含對應摻偽濃度下該種類摻偽茶油的14個脂肪酸和甘油三酯特征性物質指標含量數據。

1.3 機器學習算法

運用Python語言，利用sklearn.cross_decomposition庫中的PLS回歸函數和Linear回歸函數對數據分別構建偏最小二乘回歸(Partial Least Squares Regression, PLSR)模型和多元線性回歸模型(Multiple Linear Regression, MLR)。2種模型都采用5-折交叉驗證法進行訓練和評價，使得每個樣本都有機會作為測試集進行摻偽量的預測。采用的指標包括決定系數(Coefficient of Determination，R2)、均方根誤差(Root Mean Squared Error, RMSE)和相對誤差 (Relative Error, RE)來評價PLS和多元線性回歸模型對摻偽茶油摻偽量預測的精度。

1.4 據預處理及編程平臺

本研究所有模型和算法均基于Python 3.7編程語言在PyCharm 2018 IDE平臺 (JetBrains (Prague), Czech Republic) 進行程序編寫，所有實驗均在一臺蘋果 (Apple Computer Inc.) 筆記本上開展，詳細配置為因特爾酷睿i5 CPU (Intel (R) Core (TM) @1.70GHz)，4 GB內存，NVIDIA GeForce 320M顯卡。

2 結果與分析

2.1 偏最小二乘回歸模型和多元線性回歸模型摻偽量預測精度分析

高摻偽梯度下，PLS回歸模型對茶油摻偽量定量預測的平均R2值高達0.994，但平均RMSE值較差，為1.99，尤其是對葵花籽油、葡萄籽油、菜籽油和棕櫚油，PLS回歸模型的RMSE值都在2.2以上(表1)，這表明PLS回歸模型的預測摻偽量與真實摻偽量之間的誤差相對較大，準確率較低。低摻偽梯度下，PLSR模型對茶油摻偽量的定量預測效果較差，PLS回歸模型對茶油摻偽量定量預測的平均R2值為0.889，平均RMSE值為0.907，尤其是對棕櫚油的摻偽量預測能力最差(平均R2值=0.748，平均RMSE值=1.418)。PLS回歸模型對于高摻偽梯度下茶油摻偽量定量預測的精準率高，但準確率差，而低摻偽梯度下精準率和準確率都較差，故PLS回歸模型不能很好的實現茶油摻偽量的定量預測。

高和低摻偽梯度下，ML回歸模型對茶油摻偽量定量預測的平均R2值分別達到了0.999和0.994，平均RMSE值分別達到了0.146和0.136(表1)，ML回歸模型的精準度和準確度都要高于PLS回歸模型，ML回歸模型相比于PLS回歸模型能更好的實現茶油摻偽量的定量預測。

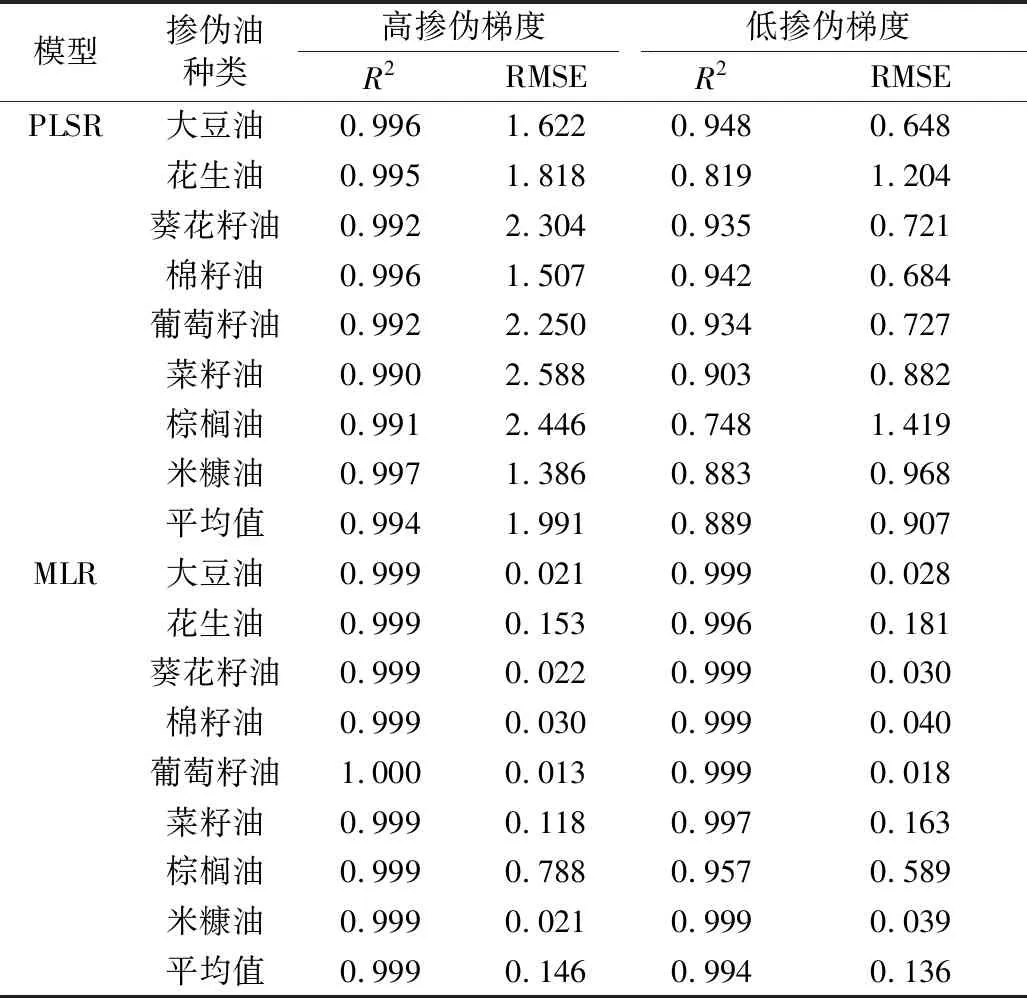
表1 不同摻偽梯度下PLS回歸模型和ML回歸模型的摻偽量預測精度指標值

針對高/低摻偽梯度下多元線性回歸模型，得到不同植物油摻偽量預測的多元線性回歸函數方程(表2)。

同時，從各類摻偽茶油樣本中的摻偽量預測結果進行分析表明，無論高摻偽梯度還是低摻偽梯度，PLS回歸模型對大部分樣本的預測值與真實值之間的相對誤差均較大(0.1～0.3)，個別樣本的相對誤差甚至達到了0.5以上，預測效果欠佳，尤其是摻偽質量分數越低，相對誤差越大，在0.3左右，個別甚至達到1.7。ML回歸模型對不同種類摻偽茶油樣本的預測值與真實值的相對誤差普遍較小(0.001～0.01)，許多樣本的相對誤差接近于0，預測效果較好。

2.2偏最小二乘回歸模型和多元線性回歸模型摻偽量預測結果的“真實摻偽量-預測摻偽量”散點圖分析

為了更為直觀地展示摻偽量預測結果，以摻入大豆油和花生油為例，基于PLS回歸模型和ML回歸模型對摻偽茶油的定量預測結果的“真實摻偽量-預測摻偽量”散點圖進行分析。散點圖中橫坐標代表樣本的真實摻偽量，縱坐標代表模型對樣本摻偽量的預測值。圖中每個點代表一個樣本，樣本點的坐標由其真實摻偽量和預測摻偽量共同決定，當樣本點越接近直線y=x，表示模型對樣本摻偽量的預測效果越好。

表2 不同摻偽梯度下多元線性回歸模型的摻偽量預測函數

高摻偽梯度下，PLS回歸模型定量預測的預測值相對于真實值存在一定程度的浮動，其中摻偽質量分數為10%、15%、20%的樣本浮動區間較大，摻偽質量分數為40%、60%、80%的樣本的浮動程度逐漸降低，預測值與真實值較為接近(圖1a和圖1b)，低摻偽梯度下，PLS回歸模型定量預測的預測值相對于真實值之間的浮動程度更大(圖1c和圖1d)。結果表明PLS回歸模型對茶油摻偽的定量預測能力較差，且隨著摻偽質量分數和摻偽梯度的下降定量預測能力更差。

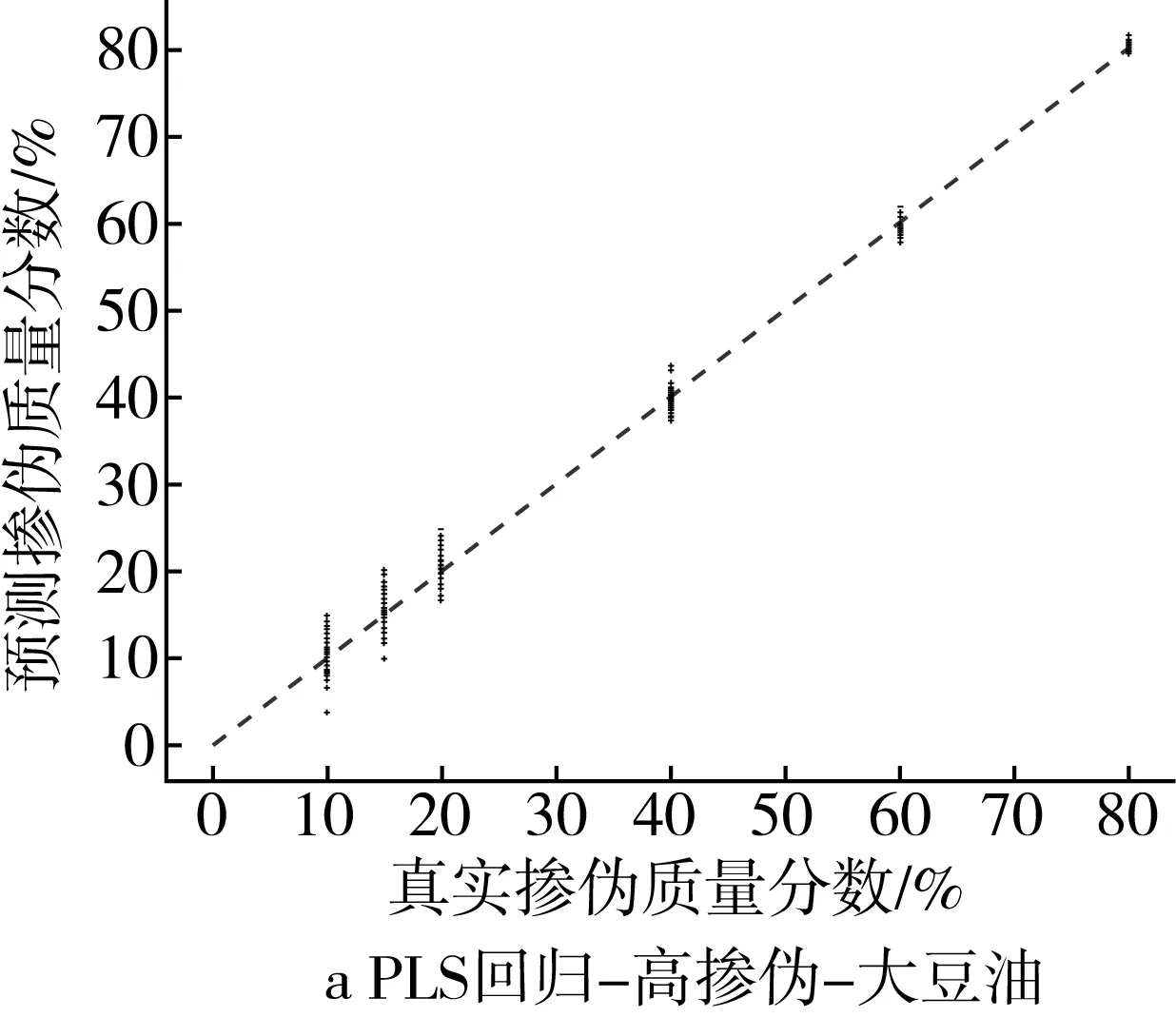
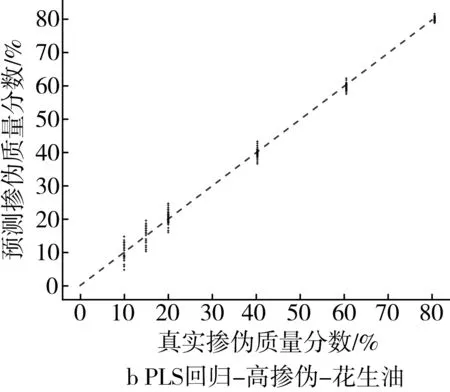
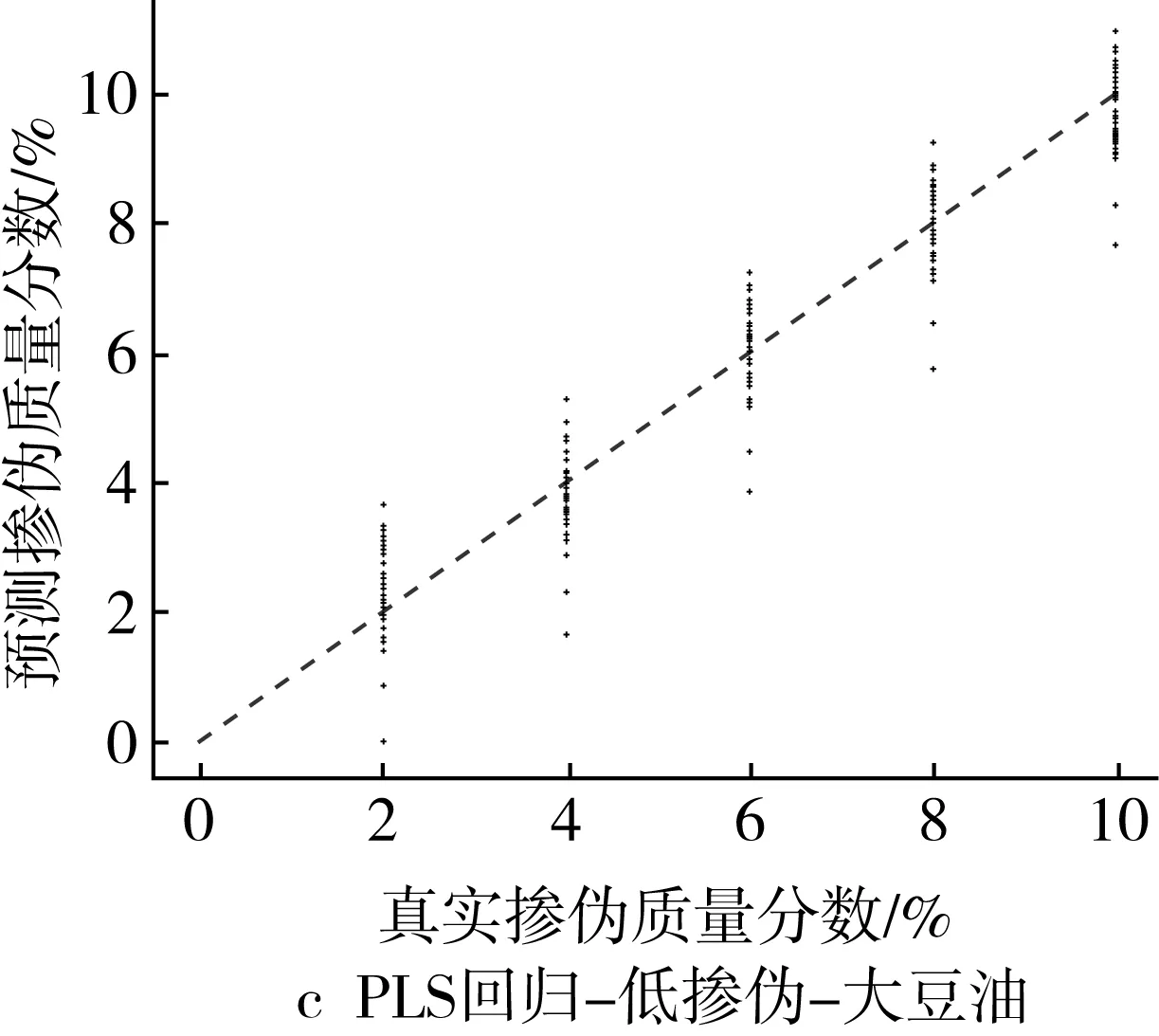
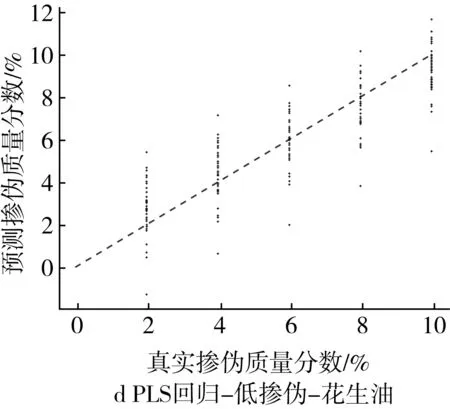
圖1 高摻偽和低摻偽梯度下PLS回歸模型定量預測結果的散點圖

高摻偽梯度下，ML回歸模型對摻偽茶油摻偽量的預測值和真實值之間的浮動程度較小，所包含的樣本點基本上分別匯聚在一條直線上(圖2a和圖2b)。與PLS回歸模型相比(圖1a和圖1b)，浮動程度明顯減小，這說明在高摻偽梯度下ML回歸模型對摻偽茶油的定量預測的相對誤差小，結果準確率高。

低摻偽梯度下，ML回歸模型對摻偽茶油摻偽量的預測值和真實值之間的浮動程度較小，所包含的樣本點基本上分別匯聚在一條直線上(圖2c和圖2d)。與PLS回歸模型相比(圖1c和圖1d)，ML回歸模型對摻偽大豆油和花生油的茶油樣本的預測值與真實值之間的浮動程度明顯減小，這說明ML回歸模型能很好的實現對摻偽茶油摻偽量的定量預測。

2.3 偏最小二乘回歸模型和多元線性回歸模型摻偽量預測結果的箱型圖分析

在高摻偽梯度下，PLS回歸模型對摻入米糠油、棉籽油的茶油樣本的定量預測效果最好，樣本的預測摻偽量與真實摻偽量之間的相對誤差大部分集中在0～0.5之間(圖3a)，對摻偽菜籽油、棕櫚油、葵花籽油和葡萄籽油的茶油的定量預測效果較差，其中對摻偽菜籽油的茶油的定量預測相對誤差結果中有接近1.4的離群點樣本(圖3a)。低摻偽梯度下PLS回歸模型對摻偽茶油定量預測的相對誤差普遍較高(>0.5)，對摻偽花生油、菜籽油、棕櫚油、米糠油的茶油的摻偽量預測的相對誤差都在2.0以上，其中對摻偽棕櫚油的茶油樣本的定量預測的相對誤差結果中有接近3.0的離群點樣本(圖3b)。這進一步說明PLSR模型對摻偽茶油的定量預測能力較差。

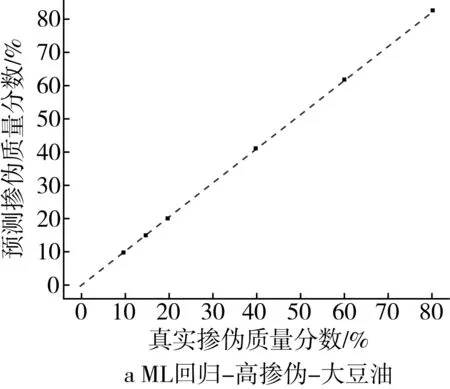
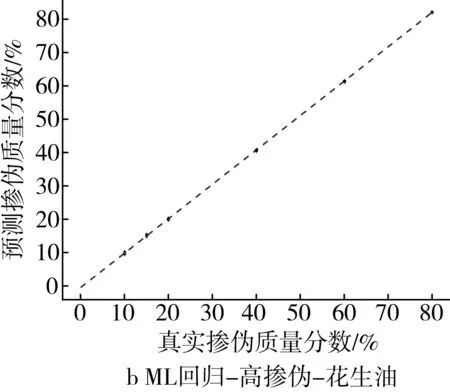
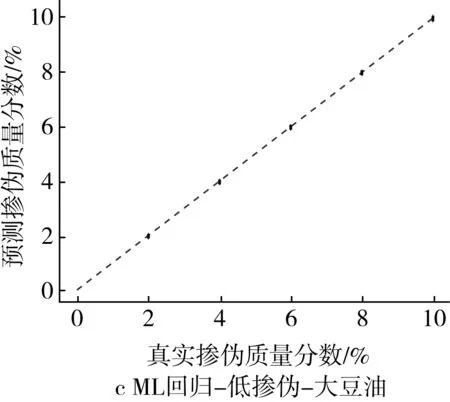
圖2 高摻偽和低摻偽梯度下ML回歸模型定量預測結果的散點圖

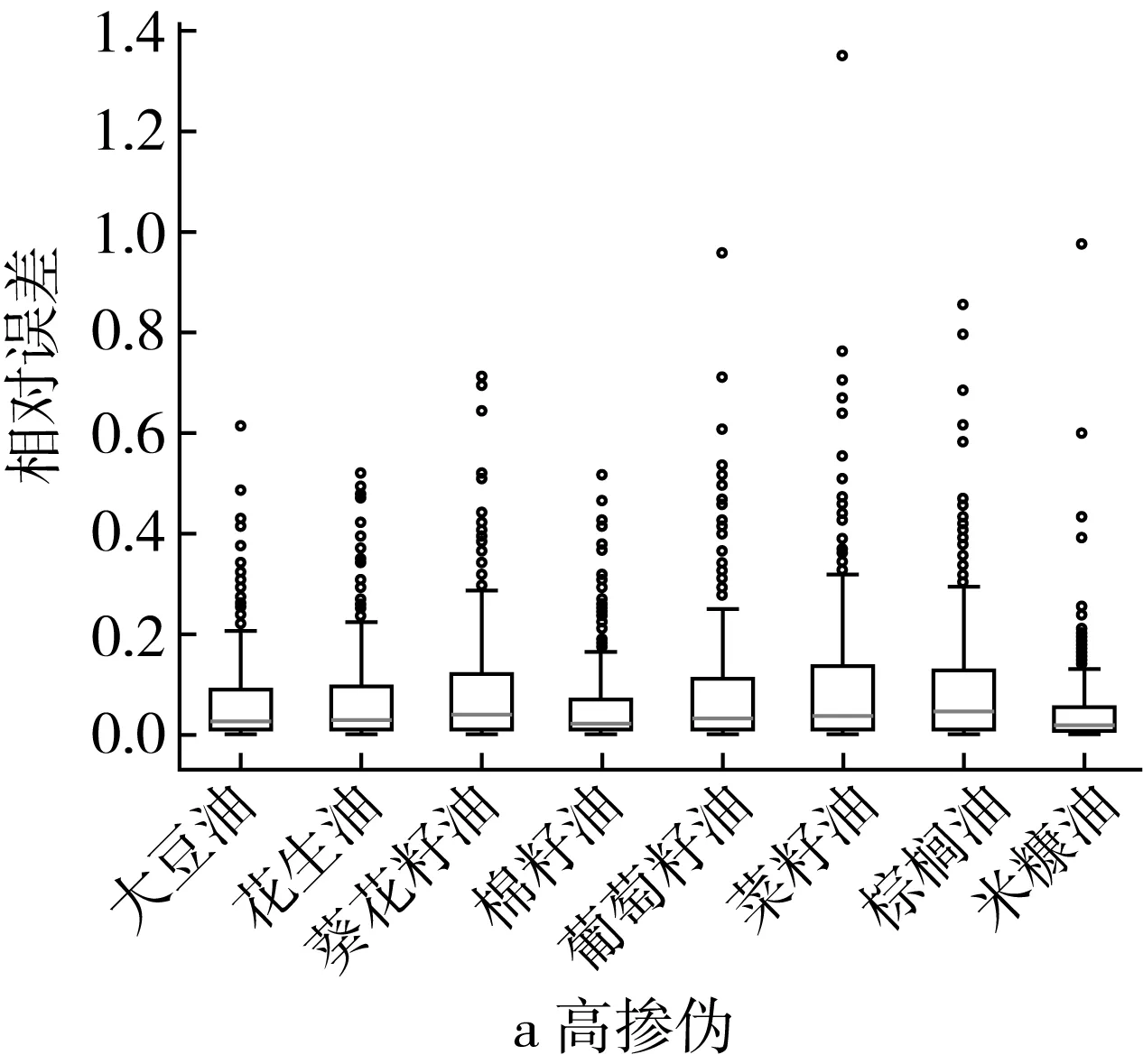
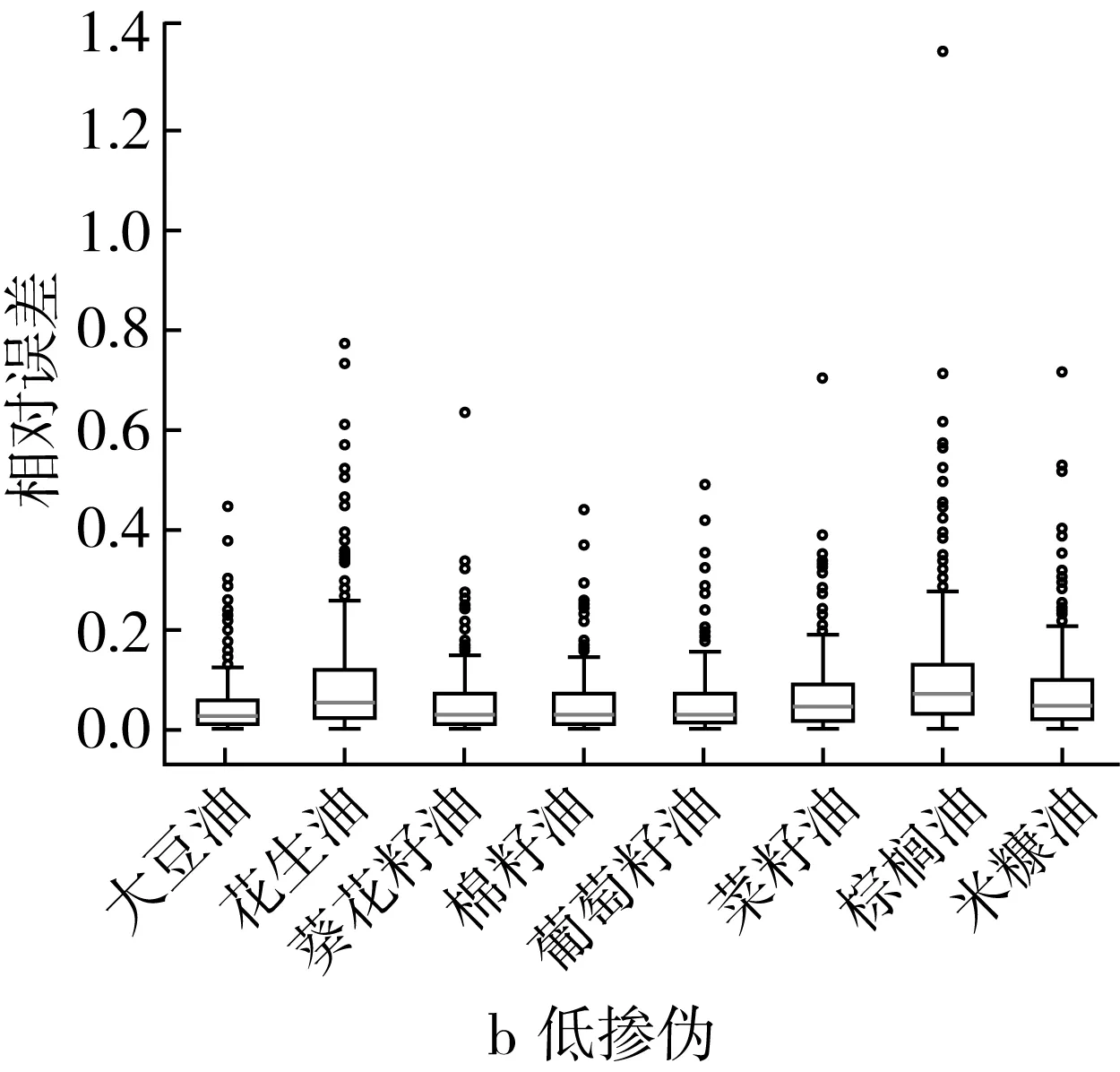
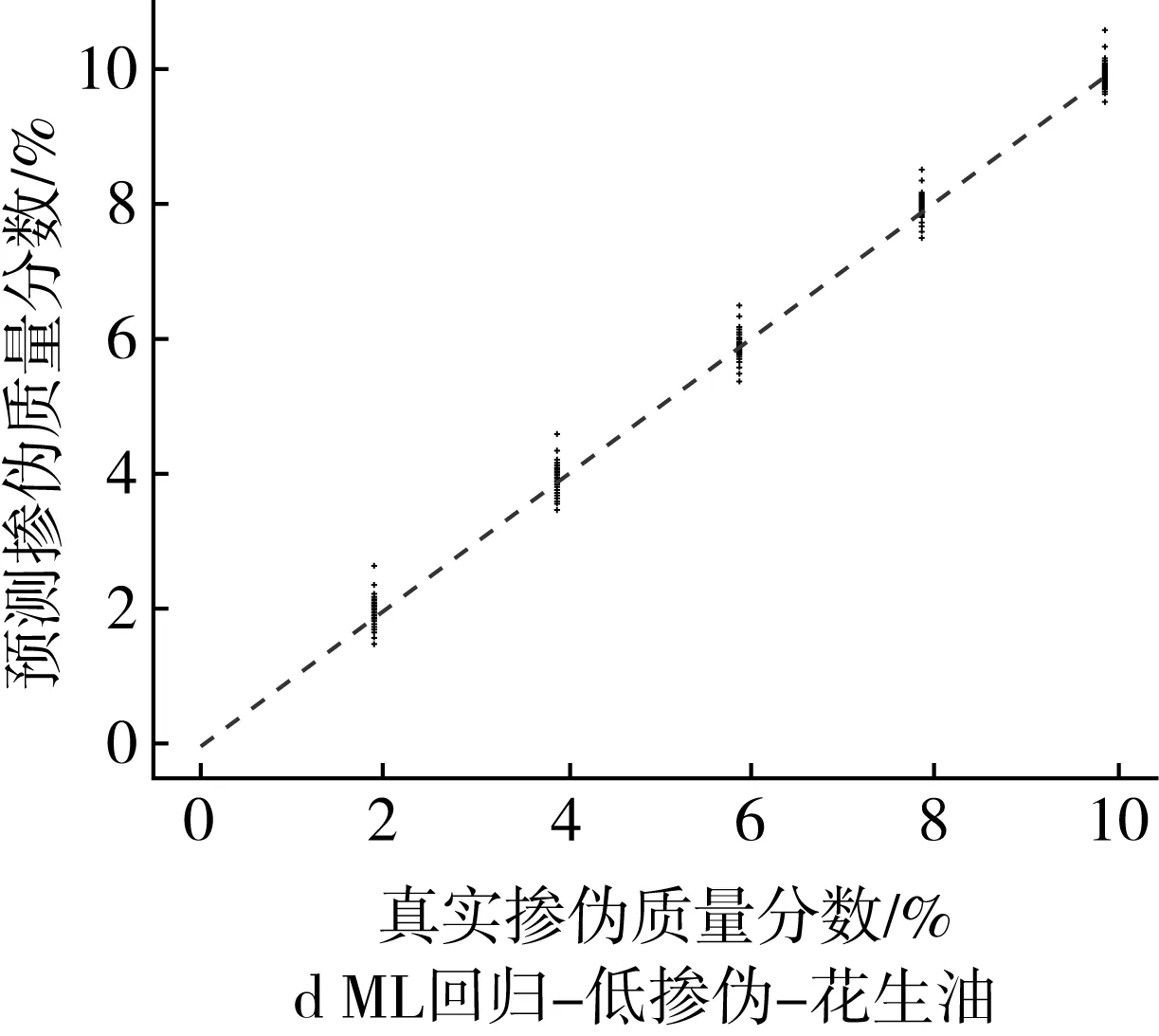
圖3 高摻偽和低摻偽梯度下PLS回歸模型定量預測相對誤差箱型圖

高摻偽梯度下，ML回歸模型對棕櫚油摻偽量的定量預測效果稍差(相對誤差≤0.25)，其次是花生油(0.05≤相對誤差≤0.1)和葡萄籽油(相對誤差≤0.05)，其他摻偽茶油樣本的定量預測結果相對誤差集中在0～0.05之間(圖4a)。ML回歸模型對摻偽大豆油、葵花籽油、棉籽油、葡萄籽油、米糠油的定量預測效果最好，明顯優于PLS回歸模型的定量預測效果，相對誤差大大降低(ML回歸模型的最大相對誤差接近0.05，PLS回歸模型的最大相對誤差接近1.4)(圖3a和圖4a)。低摻偽梯度下，ML回歸模型對棕櫚油摻偽量的定量預測效果稍差(相對誤差0.8左右)，其次是花生油(0.2≤相對誤差≤0.4)和葡萄籽油(0.2≤相對誤差≤0.3)，其他摻偽茶油樣本的定量預測結果相對誤差集中在0～0.3之間(圖4b)。ML回歸模型對大豆油、葵花籽油、棉籽油、葡萄籽油、米糠油的定量預測效果最好，明顯優于PLS回歸模型的定量預測效果，相對誤差大大降低(ML回歸模型的最大相對誤差接近1.0，PLS回歸模型的最大相對誤差接近3.0)(圖3b和圖4b)。

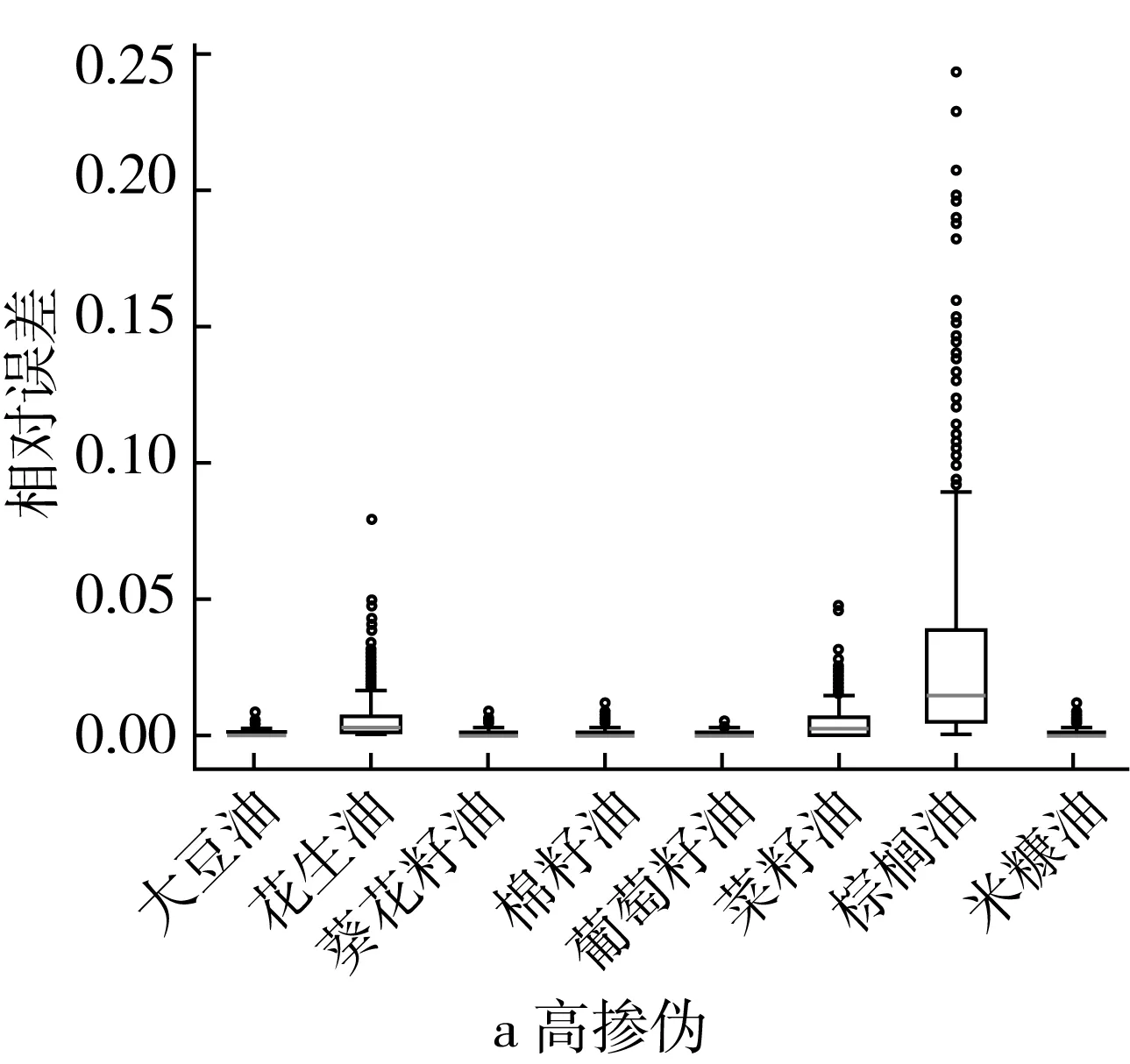
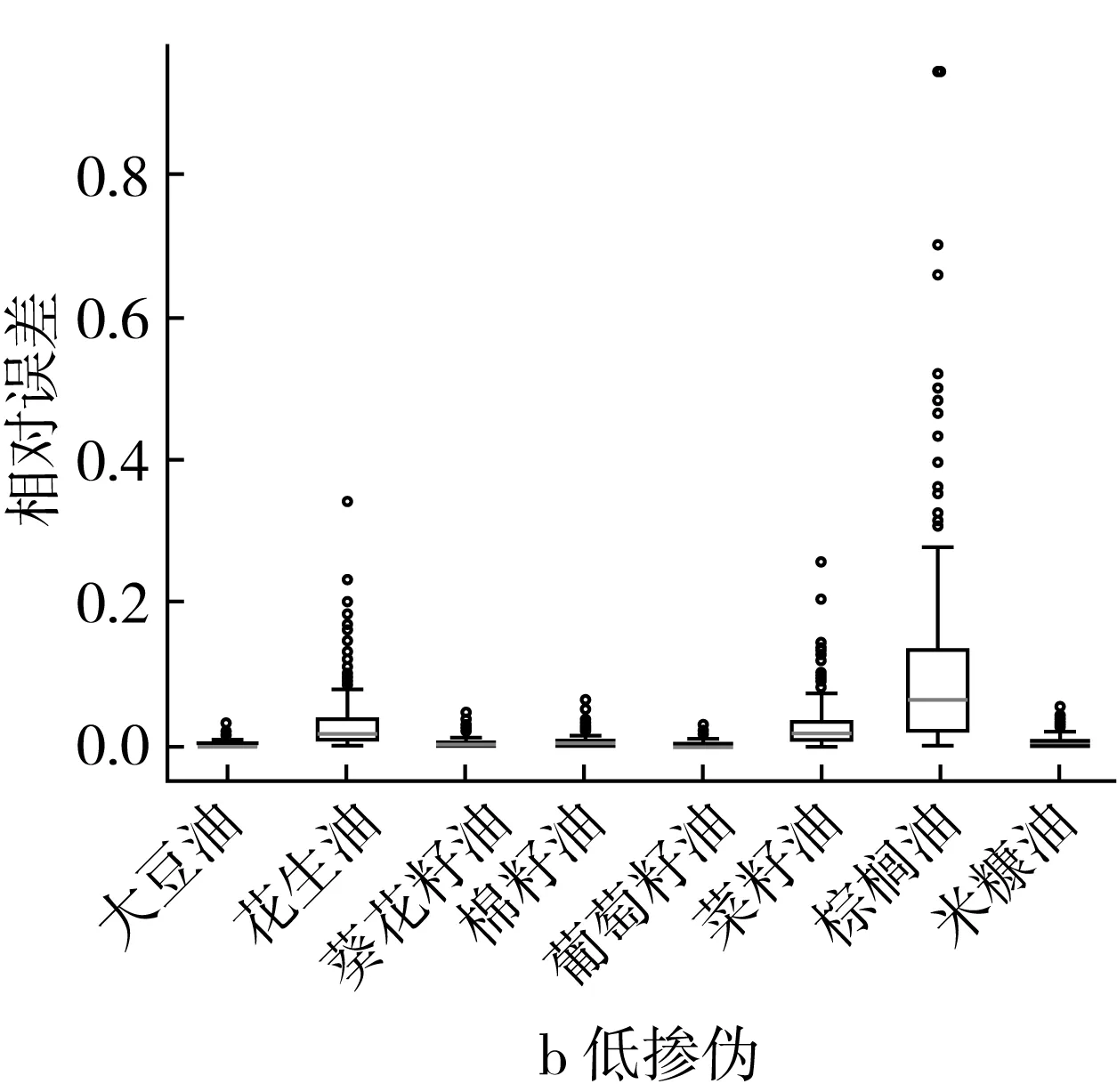
圖4 不同摻偽梯度下ML回歸模型定量預測相對誤差結果的箱型圖

結果進一步說明ML回歸模型對摻偽茶油油樣的定量預測能力較強，在不同摻偽質量分數和摻偽梯度下對摻偽茶油的摻偽量預測效果較好。

3 結論

本研究面向摻偽不同種類食用植物油的茶油摻偽量預測問題，基于14個特征性脂肪酸和甘油三酯指標，運用Python語言構建并對比分析了偏最小二乘(PLS)回歸模型和多元線性(ML)回歸模型用于摻偽茶油摻偽量的定量預測的效果。實驗結果顯示ML回歸模型的摻偽量預測能力更強，可用于不同摻偽含量和摻偽梯度茶油樣本的定量預測。

本研究構建的摻偽量預測模型可在實際的摻偽量預測場景中得到應用。基于現有摻偽茶油樣本的特征物質含量和摻偽量實驗數據對茶油摻偽量預測模型進行訓練。待模型訓練完畢后，面向摻入特定品種食用植物油的摻偽量待測定茶油樣本時，測定樣本的脂肪酸和甘油三酯含量數據，代入事先訓練好的摻偽量預測模型中，即可得到摻偽量預測值。

后續可對我國油茶籽油和常見食用植物油的甘油三酯結構開展系統性研究，以期提高油茶籽油摻偽鑒別模型的效果和能力。