“充填體-煤柱”復(fù)合結(jié)構(gòu)勢(shì)能突變破壞機(jī)理

王爍康，閆晶晶，陽(yáng)元中

（1.河北石油職業(yè)技術(shù)大學(xué)數(shù)理部，河北承德 067000；2.中國(guó)礦業(yè)大學(xué)礦業(yè)工程學(xué)院，江蘇徐州 221116）

煤炭是我國(guó)的主體能源，預(yù)計(jì)到2050 年煤炭占一次能源消費(fèi)的比重仍在50%以上[1-2]。傳統(tǒng)的粗放式開(kāi)采易造成巖層運(yùn)移、地下水資源流失、地表植被枯萎等生態(tài)問(wèn)題[3]。充填開(kāi)采能夠有效控制巖層移動(dòng)，是解決煤炭資源開(kāi)采與生態(tài)環(huán)境保護(hù)之間矛盾的重要途徑[4-5]。開(kāi)采過(guò)程中，充填體逐步置換煤柱，覆巖的支撐結(jié)構(gòu)由煤體變?yōu)椤俺涮铙w-煤柱”復(fù)合結(jié)構(gòu)（以下簡(jiǎn)稱復(fù)合結(jié)構(gòu)）。該結(jié)構(gòu)的穩(wěn)定承載既是煤炭安全開(kāi)采的重要保障，又是實(shí)現(xiàn)煤炭綠色開(kāi)采的前提。國(guó)內(nèi)外學(xué)者對(duì)煤柱與充填體的穩(wěn)定性問(wèn)題進(jìn)行了諸多理論研究與實(shí)踐探索[6-10]，學(xué)者們通常將煤柱或充填體視為柱體，頂、底板對(duì)柱體施加夾持作用開(kāi)展相關(guān)研究。對(duì)于區(qū)段式，學(xué)者們得出了較為成熟的塑性區(qū)計(jì)算方法，例如A H 威爾遜兩區(qū)約束理論、Kastner 公式等[11-12]；對(duì)于條帶式或塊段式，學(xué)者們將直接頂（或基本頂）簡(jiǎn)化為板狀結(jié)構(gòu)，在載荷的作用下對(duì)煤柱或充填體做功，從系統(tǒng)能量突變的角度分析煤柱或充填體的穩(wěn)定性[13-16]；對(duì)于不規(guī)則柱體，如邊角煤柱等，通過(guò)Voronoi 圖的方法確定出有效承載面積，從而給出不規(guī)則煤柱穩(wěn)定性評(píng)價(jià)標(biāo)準(zhǔn)[17-19]。前人成果多集中于單一承載結(jié)構(gòu)穩(wěn)定性的研究，且煤柱穩(wěn)定性的判別多以強(qiáng)度理論與經(jīng)驗(yàn)公式為主，與工程現(xiàn)場(chǎng)存在一定偏差。為此，以復(fù)合結(jié)構(gòu)作為研究對(duì)象，將覆巖、煤柱與充填體系統(tǒng)相互作用力學(xué)模型與突變失穩(wěn)數(shù)學(xué)模型相結(jié)合，揭示復(fù)合結(jié)構(gòu)突變失穩(wěn)的能量轉(zhuǎn)化機(jī)制，為煤炭資源安全開(kāi)采提供理論依據(jù)。

1 “充填體-煤柱”復(fù)合結(jié)構(gòu)承載特征

1.1 力學(xué)模型

復(fù)合結(jié)構(gòu)承受了自身上方全部覆巖質(zhì)量，以及開(kāi)采與充填空間上方部分覆巖質(zhì)量。為建立復(fù)合結(jié)構(gòu)力學(xué)模型，做出如下假設(shè)：

1）充填開(kāi)采能夠有效控制頂板，頂板下沉量相對(duì)采高是極小量，可忽略因充填先后順序造成頂板下沉量的差異。

2）充填材料能夠充滿整個(gè)采空區(qū)，凝固后形成的充填體與覆巖、煤柱始終保持相互作用關(guān)系。

3）整個(gè)采空區(qū)范圍內(nèi)充填材料力學(xué)特性相同，且煤柱與充填體均具備連續(xù)性、均勻性以及各項(xiàng)同性等性質(zhì)。

4）充填體與煤柱之間通過(guò)相互作用可形成復(fù)合承載結(jié)構(gòu)，二者之間的區(qū)別僅限于物理力學(xué)參數(shù)的的不同。

5）覆巖載荷均勻分布于煤柱與充填體上方，復(fù)合結(jié)構(gòu)變形特征可簡(jiǎn)化為平面應(yīng)變問(wèn)題。

基于巷式充填開(kāi)采特征，建立的復(fù)合結(jié)構(gòu)礦壓和力學(xué)模型如圖1 和圖2。圖中，M 為采高，m；L 為采場(chǎng)巷道寬度，m；a 為充填體寬度，m；b 為煤柱寬度，m；H 為煤層埋深，m；H1為采場(chǎng)巷道直接頂承載的覆巖高度，m；n 為復(fù)合結(jié)構(gòu)與采場(chǎng)巷道的寬度之比；Y1、Y2分別為充填體與煤柱的塑性區(qū)寬度，m。

圖1 復(fù)合結(jié)構(gòu)礦壓模型Fig.1 The rock pressure model of composite structure

圖2 復(fù)合結(jié)構(gòu)力學(xué)模型Fig.2 The mechanical model of composite structure

復(fù)合結(jié)構(gòu)承受的支承壓力p 為：

式中：ρ 為覆巖平均密度，取值2.5 t/m3。

1.2 復(fù)合結(jié)構(gòu)總勢(shì)能

復(fù)合結(jié)構(gòu)承載過(guò)程中，會(huì)產(chǎn)生塑性區(qū)而降低有效支撐面積，當(dāng)有效支撐面積減小到承載極限時(shí)將發(fā)生破壞失穩(wěn)。復(fù)合結(jié)構(gòu)彈性核區(qū)與塑性區(qū)的本構(gòu)關(guān)系不同，前者呈線性關(guān)系，而后者具有軟化性質(zhì)的非線性關(guān)系，且煤柱與充填體具有不同的物理力學(xué)參數(shù)。充填體應(yīng)力σ1與應(yīng)變?chǔ)?及損傷變量D1之間存在關(guān)系：

式中：D1=1-e-ε1/ε01；ε1為充填體的變形量；ε01為峰值載荷作用下充填體的變形量；E1為充填體的彈性模量。

復(fù)合結(jié)構(gòu)塑性區(qū)載荷ps與勢(shì)能Vs分別為：

式中：ε2為煤柱變形量；ε02為峰值載荷作用下煤柱的變形量；E2為煤柱彈性模量。

復(fù)合結(jié)構(gòu)彈性核區(qū)載荷pe與勢(shì)能Ve分別為：

覆巖下沉產(chǎn)生的重力勢(shì)能Vp為：

復(fù)合結(jié)構(gòu)總勢(shì)能為：

2 “充填體-煤柱”復(fù)合結(jié)構(gòu)突變機(jī)理

2.1 數(shù)學(xué)模型

突變理論是1 門研究控制變量發(fā)生改變導(dǎo)致?tīng)顟B(tài)變量發(fā)生突變的非線性科學(xué)，可用來(lái)分析自變量的連續(xù)改變導(dǎo)致系統(tǒng)發(fā)生突變失穩(wěn)的過(guò)程[20]。針對(duì)巷式充填開(kāi)采復(fù)合結(jié)構(gòu)突變失穩(wěn)機(jī)理的分析，狀態(tài)變量為一維變量，即復(fù)合結(jié)構(gòu)破壞失穩(wěn)。由于煤（巖）破壞的不可逆性，應(yīng)選擇狀態(tài)不可逆轉(zhuǎn)的折疊型突變模型或燕尾型突變模型。考慮到復(fù)合結(jié)構(gòu)穩(wěn)定性受采礦地質(zhì)條件、采場(chǎng)巷道采掘的相互擾動(dòng)，以及復(fù)合結(jié)構(gòu)的組成等因素影響，選擇控制變量維數(shù)更高的燕尾型突變模型，用來(lái)研究復(fù)合結(jié)構(gòu)突變失穩(wěn)機(jī)理。

燕尾型突變模型的勢(shì)函數(shù)f（x）為：

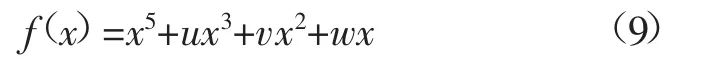
式中：u、v、w 為控制變量；x 為狀態(tài)變量。

平衡曲面方程為：

突變點(diǎn)集為：

分歧點(diǎn)集U 為：

燕尾型突變分歧點(diǎn)集U 將三維控制空間劃分成5 個(gè)區(qū)域，分別是燕翅上方、燕尾內(nèi)部、燕尾下部、左燕翅下方及右燕翅下方。發(fā)生突變的必要條件為，控制變量所確定的點(diǎn)（相點(diǎn)）隨時(shí)間的變化穿過(guò)了分歧點(diǎn)集U 的不同區(qū)域，并且它們所在區(qū)域平衡點(diǎn)的性質(zhì)發(fā)生了變化。可采用一元四次方程實(shí)根判別方法，研究各區(qū)域相點(diǎn)的性質(zhì)是否相同。

2.2 突變失穩(wěn)臨界條件

由于充填體物理力學(xué)性質(zhì)、煤層厚度及強(qiáng)度等參數(shù)對(duì)復(fù)合結(jié)構(gòu)靜載穩(wěn)定性產(chǎn)生影響。根據(jù)前期的研究工作，已得出保證復(fù)合結(jié)構(gòu)靜載穩(wěn)定的充填體物理力學(xué)參數(shù)[7]。在此基礎(chǔ)上，基于燕尾型突變理論，分別進(jìn)行求解充填體承載部分與煤柱承載部分勢(shì)能突變臨界條件。

充填體承載部分復(fù)合結(jié)構(gòu)勢(shì)能函數(shù)V1為：

式中：o 為數(shù)學(xué)符號(hào)，表示高階無(wú)窮小。

取無(wú)量綱量x=ε-2ε01作為狀態(tài)變量，且式（14）中的余項(xiàng)近似取0。構(gòu)建燕尾型突變平衡曲面方程，并整理為標(biāo)準(zhǔn)形式，得：

采充過(guò)程中，將導(dǎo)致式（17）中v 和w 發(fā)生變化。充填體承載部分，發(fā)生突變失穩(wěn)的必要條件是判別式Δ1＜0。已知a+b=nL，假設(shè)a=αL（α=0，1，2，…，n），式（17）可整理成關(guān)于Y1的一元二次方程，即：

其中：Q=（6nH+6H-5L）2ε012α4L4

式（18）的判別式滿足Δ01＞0。判別式中對(duì)比含有Q 的各項(xiàng)系數(shù)，當(dāng)系數(shù)之間相差至少2 個(gè)數(shù)量級(jí)時(shí)，只保留較高次冪系數(shù)的項(xiàng)。Δ01＞0 時(shí)，表達(dá)式化簡(jiǎn)可得：

同理可得，煤柱承載部分，系統(tǒng)發(fā)生突變的必要條件是：

其中：R=（6nH+6H-5L）2ε022（n-α）4L4

求解式（18）和式（20）并取有意義的解集，可得復(fù)合結(jié)構(gòu)保持穩(wěn)定的必要條件是充填體與煤柱塑性區(qū)寬度應(yīng)同時(shí)滿足：

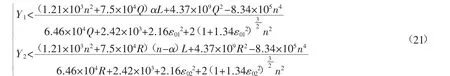
3 “充填體-煤柱”復(fù)合結(jié)構(gòu)影響因素

根據(jù)式（21），復(fù)合結(jié)構(gòu)發(fā)生突變失穩(wěn)的影響因素主要包括采場(chǎng)巷道寬度L、煤層埋深H 以及開(kāi)采階段數(shù)N 等。開(kāi)采階段可解釋為：巷式充填開(kāi)采或連采連充過(guò)程中，通常采用多輪次循環(huán)開(kāi)采的方式回收煤柱，每個(gè)循環(huán)輪次成為1 個(gè)開(kāi)采階段。以塑性區(qū)寬度作為評(píng)判標(biāo)準(zhǔn)，分別求解充填體承載部分和煤柱承載部分發(fā)生突變失穩(wěn)的臨界條件[22]。一般采場(chǎng)巷道寬度L 取4～7 m，煤層埋深L 取200～800 m，以及開(kāi)采階段數(shù)N 取2～5。根據(jù)前人的研究成果，復(fù)合結(jié)構(gòu)維持穩(wěn)定的臨界核區(qū)率取65%[23]，得到的充填體與煤柱承載部分的穩(wěn)定性臨界曲面如圖3和圖4。

圖3 充填體承載部分突變失穩(wěn)臨界曲面Fig.3 The catastrophe instability critical surfaces of the filling body part

圖4 煤柱承載部分突變失穩(wěn)臨界曲面Fig.4 The catastrophe instability critical surfaces of the coal pillar

若以采場(chǎng)巷道寬度作為不變量，復(fù)合結(jié)構(gòu)保持穩(wěn)定的最大允許煤層埋深隨開(kāi)采階段數(shù)的增加而降低。這一結(jié)果表明，充填體突變失穩(wěn)是臨近采場(chǎng)巷道采掘?qū)Τ涮铙w產(chǎn)生反復(fù)擾動(dòng)，致使其內(nèi)部累計(jì)損傷的結(jié)果。開(kāi)采階段數(shù)對(duì)充填體內(nèi)部損傷的影響表現(xiàn)為擾動(dòng)次數(shù)，采場(chǎng)巷道寬度表現(xiàn)為擾動(dòng)距離。若以煤層埋深作為不變量，開(kāi)采階段數(shù)越大，復(fù)合結(jié)構(gòu)保持穩(wěn)定的最大允許采場(chǎng)巷道寬度越小。這一結(jié)果表明，減小空頂面積可減低充填體內(nèi)部損傷值的累積程度。若以開(kāi)采階段數(shù)作為常量，復(fù)合結(jié)構(gòu)保持穩(wěn)定的最大允許煤層埋深與最大允許采場(chǎng)巷道寬度近似呈負(fù)指數(shù)函數(shù)關(guān)系，可表示為H=λeζL，采場(chǎng)結(jié)構(gòu)突變失穩(wěn)臨界擬合曲線的待定參數(shù)見(jiàn)表1 和表2。其中，R2表示擬合曲線與計(jì)算結(jié)果的相關(guān)程度。

表1 充填體承載部分?jǐn)M合參數(shù)Table 1 The fitting parameters in the filling body part

表2 煤柱承載部分?jǐn)M合參數(shù)Table 2 The fitting parameters in the coal pillar part

對(duì)比上述結(jié)果發(fā)現(xiàn)，相同地質(zhì)與開(kāi)采條件下，煤柱承載部分復(fù)合結(jié)構(gòu)發(fā)生突變失穩(wěn)的臨界曲線始終位于充填體承載部分的下方，表明煤柱較充填體更易發(fā)生破壞失穩(wěn)。這一結(jié)果可解釋為充填體剛充入采空區(qū)時(shí)處于散體狀態(tài)，只有當(dāng)充填材料凝固以及覆巖運(yùn)移對(duì)充填體產(chǎn)生擠壓，充填體才逐漸承載。而原巖應(yīng)力下，煤柱處于三向受力狀態(tài)，當(dāng)采場(chǎng)巷道采掘后，煤柱的側(cè)向壓力解除，采動(dòng)卸荷作用對(duì)煤柱造成了第1 次損傷。頂板下沉的初始階段，主要由煤柱承擔(dān)覆巖載荷，直到充填體與煤柱能夠復(fù)合承載，覆巖運(yùn)移對(duì)煤柱造成了第2 次損傷。從復(fù)合結(jié)構(gòu)的承載過(guò)程來(lái)看，充填體是以覆巖運(yùn)移為前提的被動(dòng)承載過(guò)程，而煤柱承載是受采動(dòng)卸荷與覆巖運(yùn)移的逐漸損傷過(guò)程。

4 工程案例驗(yàn)證

王臺(tái)鋪煤礦開(kāi)采煤層為XV 煤，煤層平均厚度2.4 m，傾角1°～2°。研究區(qū)域工作面走向長(zhǎng)度330 m，傾向長(zhǎng)度160 m，埋深220 m。工作面內(nèi)雙翼布置采場(chǎng)巷道，采場(chǎng)巷道與運(yùn)輸主巷夾角為50°，采場(chǎng)巷道寬度為6 m，劃分為4 個(gè)開(kāi)采階段，復(fù)合結(jié)構(gòu)寬度為18 m，即開(kāi)采參數(shù)為N=4，L=6 m，H=220 m。

將實(shí)際開(kāi)采的工作面進(jìn)行簡(jiǎn)化處理：①巷式充填開(kāi)采具有周期性，模擬全部采場(chǎng)巷道的采掘與充填得到的是周期性的數(shù)據(jù)；②建立的力學(xué)模型將復(fù)合結(jié)構(gòu)承載特征簡(jiǎn)化為平面應(yīng)變問(wèn)題，采場(chǎng)巷道長(zhǎng)度選取適當(dāng)即可；③采場(chǎng)巷道尺寸遠(yuǎn)小于工作面尺寸。

建立尺寸為400 m（長(zhǎng)）×400 m（寬）×230 m（高）的數(shù)值計(jì)算模型，工作面尺寸為120 m（走向）×100 m（傾向），走向和傾向邊界煤柱分布為140 m 和150 m。覆巖采用Mohr-Coulomb 模型，充填體與煤層采用strain-softening 模型。

4.1 應(yīng)力分布特征

各開(kāi)采階段連采連充期間，沿工作面推進(jìn)方向煤柱與充填體上方垂直應(yīng)力分布如圖5。

圖5 復(fù)合結(jié)構(gòu)垂直應(yīng)力分布特征Fig.5 Vertical stress distribution characteristics of composite structure

由圖5 可以看出：垂直方向的原巖應(yīng)力為5.42 MPa。巷式充填過(guò)程中，垂直應(yīng)力沿工作面推進(jìn)方向呈周期性分布，周期長(zhǎng)度為開(kāi)采階段數(shù)與采場(chǎng)巷道寬度的乘積。由于應(yīng)變軟化作用，充填體邊界為應(yīng)力降低區(qū)，并向內(nèi)部延伸過(guò)程中逐漸恢復(fù)；煤柱邊界出現(xiàn)應(yīng)力集中現(xiàn)象，向內(nèi)部延伸過(guò)程中先降低再逐漸恢復(fù)。

4.2 塑性區(qū)分布特征

各開(kāi)采階段結(jié)束，煤柱與充填體上方塑性區(qū)分布如圖6。

圖6 復(fù)合結(jié)構(gòu)內(nèi)塑性區(qū)分布特征Fig.6 Distribution characteristics of plastic zone of composite structure

由圖6 可以看出：煤柱與充填體的破壞形式為剪切破壞；第1 階段結(jié)束，剪切破壞發(fā)生在煤柱邊緣，而充填體內(nèi)未發(fā)現(xiàn)破壞；第2、第3 階段結(jié)束，在新充入的充填體約束邊界處，產(chǎn)生新的剪切破壞，靠近充填體一側(cè)，剪切破壞發(fā)生在第2 階段充填體上，靠近煤柱一側(cè)，剪切破壞發(fā)生在煤柱上；第4 階段結(jié)束，剪切破壞位置發(fā)生在新充入的充填體兩側(cè)，位置與第3 階段剪切破壞的位置一致；塑性區(qū)位置對(duì)應(yīng)于煤柱邊界的垂直應(yīng)力集中位置和充填體垂直應(yīng)力的谷值位置。

4.3 垂直應(yīng)力對(duì)復(fù)合結(jié)構(gòu)穩(wěn)定性的影響

分別提取上述4 個(gè)開(kāi)采階段結(jié)束后采場(chǎng)最大垂直應(yīng)力、復(fù)合結(jié)構(gòu)上方最大垂直應(yīng)力差值及復(fù)合結(jié)構(gòu)塑性區(qū)寬度的數(shù)值計(jì)算結(jié)果，復(fù)合結(jié)構(gòu)垂直應(yīng)力變化與塑性區(qū)寬度相關(guān)性如圖7。

圖7 復(fù)合結(jié)構(gòu)垂直應(yīng)力變化與塑性區(qū)寬度相關(guān)性Fig.7 Correlations between vertical stress variation and plastic zone width of composite structure

由圖7 可以看出：復(fù)合結(jié)構(gòu)塑性區(qū)寬度與最大垂直應(yīng)力差值之間存在相關(guān)性，二者的相關(guān)系數(shù)約為0.91。垂直應(yīng)力差值越大，復(fù)合結(jié)構(gòu)塑性區(qū)寬度越接近采場(chǎng)失穩(wěn)的臨界值，表明采場(chǎng)內(nèi)垂直應(yīng)力的不均勻分布是導(dǎo)致采場(chǎng)發(fā)生突變失穩(wěn)的主要原因；整個(gè)采充過(guò)程中，復(fù)合結(jié)構(gòu)最大垂直應(yīng)力相對(duì)穩(wěn)定，在1.33～1.47 倍原巖應(yīng)力之間，而采場(chǎng)內(nèi)的變量似乎只有復(fù)合結(jié)構(gòu)的成分（煤柱由充填體逐步置換）。由于充填體屬于被動(dòng)支撐結(jié)構(gòu)，采場(chǎng)巷道開(kāi)采后覆巖應(yīng)力首先作用在煤柱上方，然后隨著充填體、煤柱及覆巖的相互作用發(fā)生轉(zhuǎn)移。

因此，煤柱尺寸越小，復(fù)合結(jié)構(gòu)上方垂直應(yīng)力差值越大，采場(chǎng)結(jié)構(gòu)越容易發(fā)生突變失穩(wěn)，且突變失穩(wěn)更易發(fā)生在煤柱承載部分，這與圖3 和圖4 的計(jì)算結(jié)果相吻合。

5 結(jié) 語(yǔ)

1）分析了“充填體-煤柱”復(fù)合結(jié)構(gòu)承載特征，建立了復(fù)合結(jié)構(gòu)總勢(shì)能平衡曲面方程，基于燕尾型突變狀態(tài)變量屬性與平衡曲面方程實(shí)根數(shù)之間的關(guān)聯(lián)性，得出了以塑性區(qū)寬度為指標(biāo)的復(fù)合結(jié)構(gòu)破壞失穩(wěn)的判別公式。

2）分析了采場(chǎng)巷道寬度、煤層埋深以及開(kāi)采階段數(shù)等開(kāi)采參數(shù)對(duì)復(fù)合結(jié)構(gòu)穩(wěn)定性的影響，繪制了三者共同作用下復(fù)合結(jié)構(gòu)破壞失穩(wěn)臨界曲面，結(jié)果表明，相同地質(zhì)條件與開(kāi)采條件下煤柱較充填體更易發(fā)生破壞失穩(wěn)。

3）分析了復(fù)合結(jié)構(gòu)承載過(guò)程中垂直應(yīng)力及塑性區(qū)分布特征，發(fā)現(xiàn)復(fù)合結(jié)構(gòu)塑性區(qū)寬度與最大垂直應(yīng)力差值之間存在相關(guān)性，二者的相關(guān)系數(shù)約為0.91，垂直應(yīng)力差值越大，塑性區(qū)寬度越接近復(fù)合結(jié)構(gòu)破壞失穩(wěn)的臨界值。

4）結(jié)合工程案例，復(fù)合結(jié)構(gòu)最大垂直應(yīng)力在1.33～1.47 倍原巖應(yīng)力之間，塑性區(qū)寬度約為2.0～4.4 m之間，巷式開(kāi)采過(guò)程中，復(fù)合結(jié)構(gòu)核區(qū)率始終不低于75.6%，破壞失穩(wěn)判別公式的準(zhǔn)確性得到了驗(yàn)證。