沖擊荷載下錨固體動力學方程與數(shù)值分析

湯紅槍，黨鵬遠，陳 達

(1.河南能源化工集團 永煤公司城郊煤礦，河南 永城 476600；2.中國礦業(yè)大學 力學與土木工程學院，江蘇 徐州 221008)

隨著煤礦開采深度的增加，礦壓沖擊危險性加劇。錨桿支護動態(tài)荷載作用下的錨桿支護作用機理引起了眾多學者和工程師的密切關注[1-4]。Mc Creath等[5]通過大量實驗和理論分析對沖擊地壓巷道支護機理問題進行了研究，認為在有沖擊危險的巷道中，所選用的錨桿必須具有較好的延展性能，即錨桿具備較強的吸收彈性應變能的能力。Anders Ansell[6-7]利用落錘試驗研究了一種新型吸能錨桿的動態(tài)力學性能，指出吸能錨桿的吸能原理是錨桿和圍巖一起屈服并產(chǎn)生大塑性變形。Charlie C L等[8-9]研發(fā)了一種新型能量吸收錨桿——D錨桿，并詳細分析了D錨桿在靜力和動力荷載下桿體的力學響應。鞠文君[10]認為，沖擊地壓下錨桿支護能夠強化圍巖體整體強度，約束圍巖變形破壞，并吸收沖擊剩余能量。薛亞東等[11]對回采巷道錨桿支護進行了地震動載模擬，發(fā)現(xiàn)端錨支護巷道受動載的破壞較全錨小，表明動載巷道錨桿支護應采用端錨方式。付玉凱等[12]采用自由落錘沖擊實驗，分析了側向沖擊荷載下錨桿的動力響應。同時，在錨桿支護材料上也進行了相應的研究[13-15]，開發(fā)了超高強且具有沖擊吸能功能的高級錨桿鋼筋。

從現(xiàn)有研究成果看，錨桿支護能夠起到一定的防沖吸能作用，從而可降低災害程度[16-19]。當巷道發(fā)生沖擊地壓時，可利用錨桿的這種吸能作用，控制沖擊地壓發(fā)生時的災害效應。筆者從錨桿支護在沖擊地壓下的工作機制入手，分析錨固體在動載作用下的響應特征，探索錨桿支護在沖擊地壓下的減災機理和作用。

1 錨固體動力學方程

錨桿通過錨固段對圍巖產(chǎn)生作用，圍巖在外界荷載下產(chǎn)生變形與位移，從而對錨桿產(chǎn)生作用。目前對于靜載作用下，錨桿支護作用機理的研究已取得了很多成果，并得到廣泛應用[20-22]，但對于動載作用下錨桿支護機理的研究還不夠。在此，首先建立錨固體動力學理論模型，分別建立錨固體自由段和錨固段的動力學偏微分方程，并給出初始條件和邊界條件。

1.1 錨固體動力學模型

錨桿與圍巖組成的錨固體示意圖，如圖1所示。

圖1 錨固體示意圖

圖1中，錨桿體長為L，錨固段長為Lm，自由段長為Lz，則外露長度為(L-Lm-Lz)，截面積為Sb，截面周長為l，錨桿材料密度ρ，不計重力。在此作出如下假設：

1)錨桿體為有限長等截面均質桿，材料為質量連續(xù)分布的線性彈性體，其彈性模量為Eb(錨固體模型彈性模量)；

2)錨桿及圍巖形成的錨固體為均質，且對錨桿體的作用可以用一個線性彈簧和線性阻尼器以平行的方式耦合，其分布式彈簧系數(shù)為k，阻尼系數(shù)為η，如圖2所示；

3)深部圍巖對錨桿的作用簡化為線性分布式彈簧，其彈簧常數(shù)為kb；

4)錨桿軸向振動時錨桿、固結體及圍巖只發(fā)生線性彈性變形；

5)外界動載Q(t)沿錨桿軸線方向，且均布于錨桿末端。

圖2 錨桿示意圖

1.2 錨固體動力學方程

1.2.1自由段分析(0≤x≤Lz)

在自由段截取錨桿單元體如圖3所示。

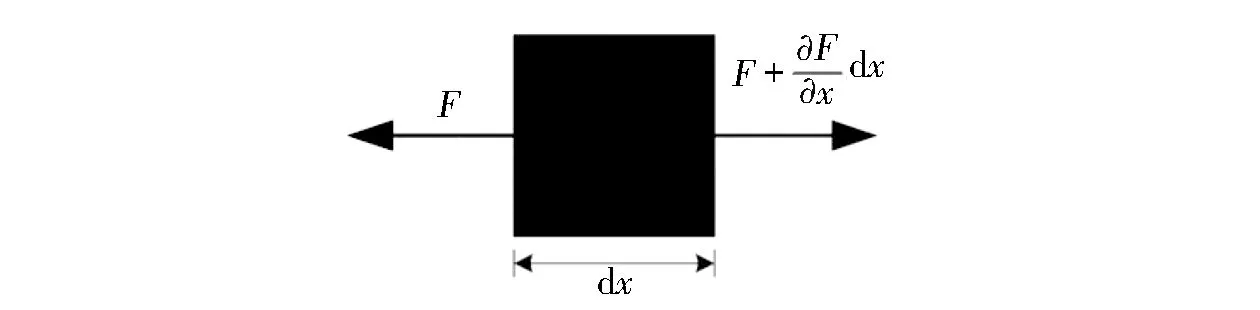
圖3 自由段錨桿微元

(1)

(2)

式中：u為錨桿體質點的位移，是x和t的函數(shù)， m；F為錨桿微元體截面的內力， N。

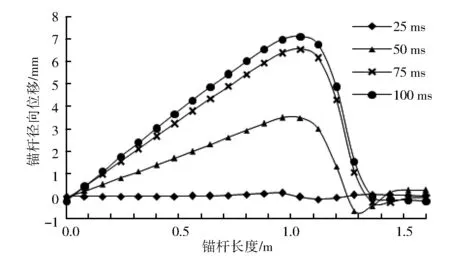
1.2.2錨固段分析(Lz

在錨固段截取錨桿單元體如圖4所示。

圖4 錨固段錨桿微元

取錨桿體微元作動力平衡分析得：

(3)

(4)

動載作用下錨桿位移沿全長偏微分方程：

(5)

方程(5)是二階偏微分方程，表征動荷載作用下錨桿與圍巖相互作用的關系。由式(5)可知，錨桿位移u(x，t)是關于錨桿長度與時間的函數(shù)，該方程的解析在數(shù)學上存在一定的困難。為了進一步揭示該方程的物理意義，采用數(shù)值模擬的方法進行分析，可揭示在沖擊荷載作用下錨桿和圍巖的動力響應特征，包括錨桿軸力、錨桿縱向及橫向位移、圍巖應力、圍巖應變、振動速度變化特征等。

2 數(shù)值計算模型

利用FLAC5.0建立平面數(shù)值模型，如圖5所示。模型尺寸1.0 m×1.6 m，單元數(shù)量為4 080個。其中，錨桿單元80個(自由段單元為60個，錨固段單元為20個)，巖石單元4 000個。采用Cable單元模擬錨桿，巖石采用Mohr-Coulomb模型；錨桿長度1.6 m，其中錨固段長度為0.4 m，自由段長度1.2 m。模型上下邊界條件為固定X、Y方向位移，并在上下邊界施加靜止邊界，四周施加自由場邊界，初始條件為靜止狀態(tài)。基于城郊煤礦現(xiàn)場勘測結果，外界輸入動荷載采用半正弦速度荷載，其方程為：v=5sin(10π×t)，頻率5 Hz，峰值5 m/s，動荷載施加位置為模型右邊界中部0.24 m處，上下各0.12 m對稱施加，作用時間為100 ms。具體圍巖和錨桿單元參數(shù)見表1和表2。

圖5 錨固體模型圖

表1 圍巖物理參數(shù)

表2 錨桿物理參數(shù)

為觀測模型各物理參數(shù)的變化規(guī)律，在模型左邊界布置圍巖振動速度監(jiān)測線，沿整根錨桿布置位移、軸力、剪切應變等參數(shù)監(jiān)測線，在離錨桿最近的圍巖處布置圍巖監(jiān)測線。模型監(jiān)測線布置見圖6所示。

圖6 監(jiān)測線布置圖

3 錨固體動力響應特征與規(guī)律

由于動力學問題會引進時間因素，導致問題的分析變得復雜，在不同時刻，動力方程可能會有不同的解，此時需要控制時間不變，分析同一時刻下錨桿與圍巖的響應規(guī)律；同時，為了揭示公式(5)的物理意義，還需要對部分關鍵點進行時程歷程分析，充分了解錨固體在不同時刻、不同位置的動力響應規(guī)律。

3.1 錨桿位移變化特征分析

3.1.1錨桿軸向位移

圖7是在沖擊荷載作用下不同部位錨桿單元軸向位移的時間歷程曲線，圖中標注表示從錨桿托盤處計算的錨桿分段長度。圖8是錨桿全長在25 ms、50 ms、75 ms、100 ms這4個時刻的軸向位移變化曲線。

由圖7可以看出，無論是自由段還是錨固段，軸向位移隨著動載作用時間的增加均在不斷增大，在動載作用結束時達到最大，離動載施加處越近最終位移越大，最大值為64 mm。其增長曲線與余弦曲線相似，增長率在動載峰值處達到最大。錨桿自由段并沒有與圍巖產(chǎn)生直接作用，而且距離沖擊荷載施加位置較遠，錨桿對沖擊荷載的響應不存在局部差異，這點通過圖8也可以看出。而錨固段與圍巖有直接作用，距離沖擊荷載施加位置又較近，該部分對沖擊荷載響應存在明顯區(qū)域差異。

圖7 錨桿軸向位移-時間歷程曲線

圖8 不同時刻錨桿軸向位移曲線

由圖8可以看出，錨桿長度在1.20～1.52 m之間，錨固段位移隨著與沖擊源距離的減小而增大；錨桿長度在1.52～1.60 m之間，錨固段位移隨著與沖擊源距離的減小而越小。最終位移在距離沖擊荷載施加位置80 mm處(即整根錨桿長度95%，錨固段長度80%處)達到最大。錨固段單元之間具有相對位移和整體位移，整體位移即自由段位移為43 mm，最大相對位移為21 mm，占整體位移的48.8%，而自由段只有整體位移。這是由于動載在錨桿體和巖體中產(chǎn)生的位移不一致，圍巖與錨桿發(fā)生了相對位移，錨桿的整體位移即圍巖的位移。

3.1.2錨桿徑向位移分析

圖9是在沖擊荷載作用下不同部位錨桿單元徑向位移的時間歷程曲線。圖10是錨桿全長在25 ms、50 ms、75 ms、100 ms這4個時刻的徑向位移變化曲線。

由圖9可以看出，在25 ms之前，錨桿幾乎沒有徑向位移，這也可以通過圖12中25 ms的曲線看出，這是因為半正弦動載在剛開始的時候速度并不大，對錨桿的影響也不明顯。25 ms之后，徑向位移隨著時間的增加而不斷增大，在85 ms達到最大，之后不再變化。說明25 ms后，動載對錨桿開始產(chǎn)生作用，85 ms后動載振動速度下降，對錨桿的作用也隨之減少。錨桿起始點(托盤處)和錨固段末端0.2 m范圍內的錨桿徑向位移在整個沖擊過程中變化都很小，最大不超過1 mm。

圖9 錨桿徑向位移-時間歷程曲線

圖10 不同時刻錨桿徑向位移曲線

由圖10可知，25 ms后，錨桿長度方向1.02 m(即整根錨桿長度63.75%，自由段長度85%處)處徑向位移始終最大，在85 ms達到最大值，最大值為7.13 mm。以錨桿1.02 m處為界，隨著距該處距離的增加，錨桿徑向位移不斷減小。整體趨勢是中間位移大，兩邊位移小，而錨固段徑向位移變化率大于自由段。由于錨固段受到圍巖約束，錨桿托盤處對錨桿位移也有約束，而自由段錨桿沒有位移約束，可以沿徑向振動，所以錨桿兩邊位移小，中間位移大。自由段不同位置距動載距離不同，而動載對其作用與其距離呈正相關關系，加之錨固段圍巖對距其較近的自由段錨桿的約束效果的綜合作用，最終呈現(xiàn)出在自由段85%處位移最大的現(xiàn)象。而位移最大出現(xiàn)的位置與動載的作用效果和錨固段圍巖約束效果的相對強弱有關。

3.2 錨桿軸力變化特征分析

圖11和圖12分別是在25 ms、50 ms、75 ms、100 ms時錨桿軸力和剪切應變曲線。

圖11 不同時刻錨桿軸力曲線

由圖11可知，100 ms時，錨固段不同位置錨桿軸力不同，當錨桿長度處于1.2～1.6 m(錨固段范圍)之間時，隨著錨桿長度的增加軸力不斷減小。對比錨固段和自由段軸力可以發(fā)現(xiàn)，錨固段軸力比自由段軸力要小，在軸力增長時錨固段增長速度也小于自由段增長速度，在自由段與錨固段分界處，軸力變化幅度較大，錨桿的軸力是由于圍巖與錨桿的相對位移產(chǎn)生的，錨固段圍巖與錨桿相對位移較自由段小，所以自由段軸力較錨固段大。

圖12 不同時刻錨桿剪切應變曲線

由圖12可以看出，自由段錨桿剪切應變變化不大，錨固段剪切應變隨錨桿長度增加不斷減小，這與錨固段軸力變化趨勢基本吻合。在自由段與錨固段分界點位置即錨桿長度為1.2 m處，錨桿剪切應變急劇增大，在此處錨桿軸力也變化較大，這種劇烈變化程度隨著動載作用時間增加而進一步加深。該位置最有可能發(fā)生局部破壞，從而導致錨桿整體失效。所以在沖擊荷載作用下錨桿的破壞過程中，自由段與錨固段分界點位置是一個關鍵控制點。另外，沖擊荷載對錨桿的影響有滯后效應，即沖擊荷載發(fā)生一段時間后錨桿才有響應。

3.3 圍巖位移變化特征分析

此處圍巖指的是離錨桿最近處同一監(jiān)測線上的圍巖，如圖6中所示的圍巖監(jiān)測線。

3.3.1X方向(軸向)位移分析

圖13中橫坐標的距離是指沿錨桿始端(模型左邊界)到錨桿終端(模型右邊界)的距離。由圖可以看出，隨著動載的施加，圍巖在X方向位移不斷增大，自由段錨桿區(qū)域圍巖X方向位移近乎直線增加，在100 ms之后穩(wěn)定下來。不同位置最終位移雖不相同但相差不大，最大相差2.6 mm。這說明自由段錨桿范圍圍巖沒有相對位移，只有整體位移，因為這部分圍巖距離沖擊荷載施加位置較遠，受沖擊荷載影響不明顯，不存在局部差異。而錨固段錨桿區(qū)域圍巖受沖擊荷載影響明顯，該范圍圍巖在X方向位移的增長速度先逐漸增大后逐漸減小，在50 ms時達到最大，位移增長曲線與余弦曲線相似。該區(qū)域圍巖最終位移最大相差7.1 mm，說明該區(qū)域受沖擊荷載影響較大，對沖擊荷載響應存在區(qū)域差異。

在錨固段，圍巖X方向位移隨著錨固段長度增加而增大，最終位移在距離沖擊荷載施加位置8 cm處達到最大，隨后減小。錨固段圍巖之間具有相對位移和整體位移，整體位移即自由段圍巖位移，最大相對位移為2.19 cm，占整體位移的51.6%，這一點與錨桿位移的分析基本一致。

圖13 不同時刻圍巖X方向位移-距離曲線

3.3.2Y方向(徑向)位移分析

圖14是圍巖在25 ms、50 ms、75 ms、100 ms時同一監(jiān)測線上圍巖Y方向位移曲線。

由圖14可以看出，同一時刻圍巖在Y方向上位移隨距離變化曲線的最大特征就是中間大兩邊小。具體來說，是在距離為1.02 m處位移達到最大，最大位移為7.37 mm。在25 ms之前圍巖Y方向上的位移幾乎為0；25 ms之后，在距離為0～1.02 m之間時，位移隨著距離增加而增大，增長率隨著時間增加而變大。在距離為1.02～1.40 m之間時，位移隨著距離增加而迅速降低；在距離為1.40～1.60 m之間時，位移接近為0，變化不大。這說明沖擊荷載對施加位置附近圍巖Y方向位移影響不大。

圖14 不同時刻圍巖Y方向位移-距離曲線

3.4 圍巖表面振動速度變化特征分析

圖15是圍巖表面不同時刻振動速度隨距離變化的歷程曲線。圖16是不同時刻左邊界淺部圍巖隨距錨桿始端距離的變化曲線。

圖15 邊界圍巖振動速度-時間歷程曲線

由圖15可以看出，圍巖表面振動速度整體呈現(xiàn)先增大后減小最后保持不變的變化規(guī)律。在60 ms左右達到最大振動速度，最大值為0.62 m/s。振動速度最大值到達時刻比動荷載峰值到達時刻延遲10 ms，且左邊界圍巖振動速度峰值遠小于動載峰值，動荷載在傳遞過程中不斷被錨固體耗散，最終到達邊界的振動是錨桿系統(tǒng)未吸收的能量，并會以動能的形式釋放出去。

由圖16可以看出，同一時刻圍巖淺部不同位置的振動速度基本一致，動荷載在傳遞過程中不斷擴散，這種擴散范圍隨著傳遞距離增大而變大，不過同一波陣面處巖石振動速度相同。動載從圍巖深部通過錨固體傳遞到圍巖表面，同一時刻整個邊界上的振動速度基本相同。對于動載施加范圍(以錨桿為對稱軸，對稱分布錨桿上下側0.12 m范圍內)，動載傳遞擴散至圍巖表面，作用范圍至少增大了3倍，擴散范圍與圍巖參數(shù)和錨桿參數(shù)有關。動載傳遞擴散范圍越大越有利于圍巖吸收能量，通過調整支護參數(shù)，可以改變擴散范圍，從而改善圍巖吸能性能。

圖16 不同時刻邊界圍巖振動速度

4 討論

由數(shù)值模擬結果分析可知，①錨桿位移最大出現(xiàn)的位置與動載的作用效果和錨固段圍巖約束效果相對強弱有關；②在沖擊荷載作用下的錨桿破壞過程中，自由段與錨固段分界點位置是一個關鍵控制點；③沖擊荷載對施加位置附近圍巖Y方向位移影響不大；④圍巖的吸能特性可以通過支護參數(shù)的調整而得到改善。

根據(jù)能量理論，沖擊地壓是由于煤巖體破壞時釋放的能量大于其吸收能量所致，即剩余能量的釋放是沖擊礦壓發(fā)生的根本原因。如果錨固體可以吸收掉部分或全部剩余能量，沖擊礦壓災害程度就會得到降低，甚至不會發(fā)生。在錨固體中錨桿是最主要的吸能構件，其吸收能量可以由其工作特性曲線確定，錨桿吸收的能量就等于其工作阻力(軸力)對變形量的積分。圖17是錨桿支護的一般工作特性曲線，圖中陰影面積即為最大吸能值[10]。

圖17 錨桿吸能原理

與圍巖相比，各種支護方式的承載能力都很小。與其他支護方式相比，錨桿具有良好的延展性，可與圍巖同步協(xié)調變形。錨桿這種柔性特征，使其對于沖擊荷載有良好的適應能力，錨桿對于沖擊荷載不是硬頂，而是讓壓，在保護自身不被破壞的前提下始終給圍巖一定約束力，控制圍巖變形和進一步的破壞。因此，錨桿支護的本質作用，無論是沖擊還是非沖擊地壓巷道，均是通過保持圍巖的完整性使圍巖承載能力不降低或少降低。錨桿支護與圍巖共同承受沖擊荷載，因此，要求錨桿應具有足夠的抗沖擊能力[16]，避免錨桿受較大沖擊荷載后破斷，失去支護作用。

5 結論

1)動載作用過程中，錨桿軸力先基本保持不變，而后迅速增大。錨固段軸力比自由段軸力小，錨固段增長速度也小于自由段增長速度，在自由段與錨固段分界處，軸力變化幅度較大。

2)動載作用過程中，自由段與錨固段分界點位置剪切應變急劇變化，這種劇烈變化程度隨著動載作用時間增長而進一步加深。

3)動荷載在傳遞過程中不斷被錨固體耗散，最終到達圍巖表面的是錨固系統(tǒng)未吸收的能量，并以動能的形式釋放出去。

4)動荷載從深部通過錨固體傳遞到圍巖表面，作用范圍成倍增大，動載傳遞擴散范圍越大越有利于圍巖吸收能量。通過調整支護參數(shù)，可以改變擴散范圍，從而改善錨固體吸能性能。