一種基于時空位置預測的空間眾包任務分配方法

徐天承 喬少杰 武 俊 韓 楠 岳 昆 易玉根 黃發良 元昌安

1(成都信息工程大學軟件工程學院 成都 610225) 2(西南財經大學證券與財經學院 成都 610074) 3(成都信息工程大學管理學院 成都 610225) 4(云南大學信息學院 昆明 650500) 5(江西師范大學軟件學院 南昌 330022)6(南寧師范大學計算機與信息工程學院 南寧 530023)7(廣西教育學院 南寧 530023)

眾包的概念源于“外包”、“承包”，外包與承包強調的是專業化團隊長期穩定的合作，而眾包則不同，將復雜的任務拆分為細粒度的任務，調動個體用戶積極參與，尋求跨專業領域知識為工作成果帶來創新.當前移動和可穿戴設備的普及不僅豐富了人們的日常生活，同時開辟了一種新的工作模式：空間眾包(spatial crowdsourcing).空間眾包相較傳統眾包，需要眾包工作者在真實世界中，物理移動到任務所標注的特定地點，完成任務要求，這一模式在生活中存在廣泛的應用場景(例如：滴滴打車、美團眾包)，它可以幫公司企業節省大量成本.

空間眾包框架中任務請求人可以通過眾包平臺發布空間任務，例如觀察咖啡店是否擁擠、監控某條路段的交通狀況等，并交付給真實世界中的眾包工作者來完成空間任務.服務器需要基于空間任務和眾包工人的位置以及其他約束對其進行分配，這一過程被稱為眾包任務分配問題.在真實的空間眾包平臺中任務和工人都是動態出現的，如果不考慮任務/工人的動態性，則無法獲得最佳的分配結果.而現實生活中眾包任務的發布和眾包工人的登錄往往具有非常復雜的動態規律，使得傳統的機器學習和統計學方法難以對任務/工人的發布分布進行準確預測.

通過分析滴滴出行分享的GAIA數據集，可以發現每天同一地點的任務發布數量均是隨時間呈周期變化的.如圖1所示，該圖統計了以各興趣點(point of interest, POI)為中心，半徑500 m內每日不同時間發生的任務數量.橫軸為按小時劃分的一天，縱軸為任務發布的數量.每個種類的線均有7條，代表一周內的7天，每種線后的陰影區域代表該POI處發布任務數量隨時間變化的趨勢.從圖1中可以發現，景點2附近在19點時大概率會出現任務數量的下降，而景點1卻沒有這種現象；火車站每日的任務數量高峰期在16～18點產生，而景點1一般在19～23時達到高峰.這表明，同一區域每日任務發布的數量具有相似的變化走勢.通過上述分析，可以得出結論：進行未來時刻任務時空分布預測時需要依據過去的任務分布，將時間和空間作為預測所需的特征學習.

Fig. 1 Quantity trend of different released POI tasks圖1 不同POI任務發布數量趨勢圖

目前已有許多關于空間眾包任務分配的研究，但現有的空間眾包任務分配方法通常存在2個方面的局限，有待進一步完善.

1) 傳統的任務/工人分布預測方法很少使用工人和任務的時空特征，且一般基于網格進行預測，但網格的不同劃分會影響到預測結果的準確性，并且很難找到最優的網格劃分方法.本文提出基于軌跡的任務分布預測方法和基于二維核密度估計的工人分布預測方法，學習歷史數據中任務/工人的時空特征，實現更精確的任務分配.

2) 空間眾包需要較快的任務分配效率，面對大規模的時空數據，計算分配的時間代價過大會導致結果沒有應用價值.本文提出了一種基于任務/工人預測進行任務分配的方法，以最大化目標函數為目的，可以在線性時間內得到有效的任務分配結果.

針對上述不足，本文對在線情景下空間眾包任務分配問題進行了研究，設計了一種基于位置預測的空間眾包任務分配方法，可以有效地計算全局最優的任務分配問題.本文的主要貢獻有3個方面：

1) 提出了基于軌跡的任務分布預測模型.不同于網格劃分的整體分布預測方法，本文基于拐點劃分軌跡，使用軌跡聚類算法獲得高流量的熱點軌跡，基于軌跡使用圖卷積來捕獲任務分布的空間特征，并使用核密度估計預測任務在軌跡上發布的具體位置，給出了計算預測所得任務價值的方法，方便后續任務分配時尋找最優解.

2) 提出基于核密度估計的工人分布預測模型.先通過二維核密度估計來表示空間任務的分布，使ConvLSTM能更好地提取任務分布的空間特征，對于預測得到的空間分布核密度估計矩陣，提出了一種基于消減數量的方法來還原真實的任務分布.

3) 提出了一種基于位置預測的任務分配方法.依據任務和工人間的位置關系，計算每個任務的可用工人集，以此來創建二分圖，設定搜索增廣路徑上限次數，優先選擇權值高的任務進行分配，并針對預測任務設置了單獨的權值比較方法，能在多項式時間復雜度內尋找盡可能好的任務分配組合.

1 相關工作

與傳統眾包技術不同，空間眾包需要基于位置信息進行工人任務間的分配.按照任務復雜度可將任務分為原子任務和復雜任務2種，原子任務可視為能由一位工人完成的簡單任務，復雜任務可以劃分為多個原子任務，需要多種特定技能才能完成，本文將任務設定為原子任務.按照任務發布模式，可分為服務器分配任務(server assigned tasks)模式和工人選擇任務(worker selected tasks)模式2種，現有的空間眾包系統大多使用服務器分配任務模式，在該模式中由服務器將任務分配給適當的工人，這種方法相較后者可以盡可能地減少無人接受的任務，并實現一些系統優化目標，如：技能覆蓋且成本最小.按任務的物理位置，可以分為特定點、特定區域和特定路線3種，這3種任務位置種類分別要求：到達一個特定的坐標點，到達特定的建筑區域，從起始點提取特定物品交付給目標客戶.為了簡化問題，現有的研究大多是基于特定點的眾包任務研究.按照服務器分配策略中數據的狀態，可以分為離線場景和在線場景，離線場景下服務器在一開始就可以獲取完整的信息，在線場景下工人和任務的登錄信息是動態的，算法將以數據流的形式接受工人和任務的登錄信息.現有的大部分研究都是基于離線場景的假設，沒有考慮到空間眾包任務分配的時空特性，不能得到全局最優分配結果.

文獻[7]首先提出了空間眾包平臺上的任務分配問題，設定服務器統一管理所有的任務和工人位置信息，以最大化任務分配數量為目的利用貪心策略將任務分配給各個工人.文獻[8-11]僅考慮了當前系統中存在的工人和任務，忽略了動態變化的任務和工人，無法得到最優的分配策略.文獻[12]最大化工人的收入為目標，并針對任務的動態性設計了一種平衡影響因素的路線推薦算法，但是該算法沒有考慮動態加入系統的工人.文獻[13]提出了一種基于位置熵最小優先級的候選工人算法，通過計算曼哈頓距離獲得候選工人，再基于決策樹進行任務分配；文獻[14]考慮到工人是動態移動的，設計了貪心算法和極值算法2種近似算法，并提出了一種基于反饋的合作機制進行任務分配；但文獻[13-14]均忽略了動態加入系統的任務.文獻[15-16]以在線算法(online algorithm)的方式來解決新加入系統的空間眾包任務分配問題.文獻[15]考慮工人—項目—任務的三色效用，設計了基于skyline查詢的解決方案；文獻[16]提出了一種基于空間感知多智能體的動態優化算法，并通過基于網格的空間優化方法來分解眾包問題，以便解決大規模數據；但這些方法的時間復雜度較高，難以應用于真實的眾包平臺.文獻[17]通過預測的方式預估工人和任務在未來時刻的空間分布，基于預測得到的數據以最大化分配質量分數為目標，基于貪心算法進行分配.文獻[18]提出了三階段的啟發式算法求解最佳任務分配，通過預估每個工人的可用時間預測工人未來時刻的軌跡，盡可能地最大化工人完成任務的數量，使得工人的移動距離均勻.但上述基于預測的方法沒有考慮到任務的分布與時間變化的關系，且在分布預測中均使用基于網格的預測方法.本文將以最大化分配價值，最小化工人移動距離為目標設計任務分配方法.

2 問題描述

本文要解決的問題中包含2種實體對象，在一個時間實例集

P

={1,2,…,

p

,…}中，實體定義如下：

定義1.

空間任務

t.

表示為

t

=〈

t.s

,

t.l

,

t.e

,

t.v

〉是一個在

t.s

時刻發生

t.l

位置的任務，該任務在

t.e

時刻前完成被認為是有效的

.

完成該任務后會產生

t.v

的價值，其中

t.l

為真實空間中的坐標(

x

,

y

)，實驗中將其視作二維數據空間的一個點

.

定義2.

眾包工人

w.

表示為

w

=〈

w.l

,

w.v

〉，表示一個在時刻

p

位置在

w.l

處的眾包工人，其移動速度為

w.v.

為簡單且不失一般性，本文假設每個空間任務只需要分配一個眾包工人，任務需要的處理時間為0，即眾包工人只要到達任務處即完成任務

.

定義3.

最大價值最小成本任務分配問題

.T

為時刻

p

系統中現有的空間任務和預測得到的空間任務組成的集合；

W

為時刻

p

系統中現有的眾包工人和預測得到的眾包工人組成的集合；

I

為時刻

p

的任務分配集，由一組有效的〈

t

,

w

〉分配對組成，其中

t

∈

T

，

w

∈

W

，分配對〈

t

,

w

〉需要滿足工人能在任務截止時間前到達任務所在的位置，且同一時間一個工人只能被分配到一個任務

.

基于任務和工人相關定義，最大價值最小成本任務分配問題可以定義為：在給定的時間實例集

P

中，最大價值最小成本任務分配問題的目標為

(1)

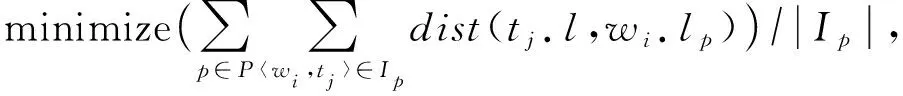
(2)

其中，

dist

(

t.l

,

w.l

)表示任務

t

到工人

w

的歐氏距離，真實情景下的軌跡分布難以類比為“棋盤格”狀，利用曼哈頓距離計算得工人距離并不準確，本文計算

dist

(

t.l

,

w.l

)是為了對比不同分配間距離的相對大小進行擇優，使用歐氏距離計算的效果更準確，故本文選擇使用歐氏距離作為不同分配對間的成本度量

.

|

I

|表示分配對的個數

.

最大價值最小成本任務分配問題的目標是最大化分配集

I

的價值和，并最小化分配集

I

中眾包工人到空間任務的平均距離

.

3 基于軌跡的任務分布預測模型

空間眾包中任務的出現受物理世界中時間和空間因素影響，其中任務請求人的行為模式在任務分配中發揮關鍵作用.空間眾包平臺中，眾包工人接收任務后需要移動到任務標注的位置，可以認為眾包任務的發布位置依附于眾包工人的軌跡，分析數據集可知不同地點的任務發生數量按時間呈周期性的模式變化.本節給出一種基于圖卷積神經網絡的模型，該模型利用軌跡聚類捕捉任務分布時間空間相關性，可以高效地估計未來的任務分布及數量.

3.1 基于軌跡的位置信息提取

受到Lee等人提出的分段及歸組框架通過軌跡挖掘得到路網信息的啟發，本節通過基于特征點的街角提取(characteristic point-based road corner extraction, CP-RCE)選取工人軌跡中的拐點，使用拐點劃分軌跡，并設定軌跡間的距離函數使用DBSCAN算法得到處理后的軌跡圖.此外，分時段選出任務發生數量高于閾值的軌跡，作為預測任務發布位置的基礎，通過后續模型學習其中的空間特征進行任務分布的預測.由圖1的分析可知每日不同POI中任務發生的數量隨時間變化的趨勢是相似的，可以認為每日相同時間段有相同的任務分布模式.假設前后兩日擁有相似的任務分布模式，那么在第

a

日的

p

時使用的圖結構是基于第

a

-1日的

p

時的數據生成的.本文提出的基于軌跡的位置信息提取方法包含如下2個關鍵步驟.

1) 提取軌跡拐角.通過分析數據集中的GPS軌跡，使用基于特征點的街角提取方法提取軌跡中的拐角.具體的說，CP-RCE方法以定寬的窗口來遍歷GPS軌跡，在中心點的左右通過線性擬合的方法生成2條直線，通過計算軌跡點在兩直線上投影間的夾角，夾角大于閾值的軌跡點就是代表拐角的特征點.

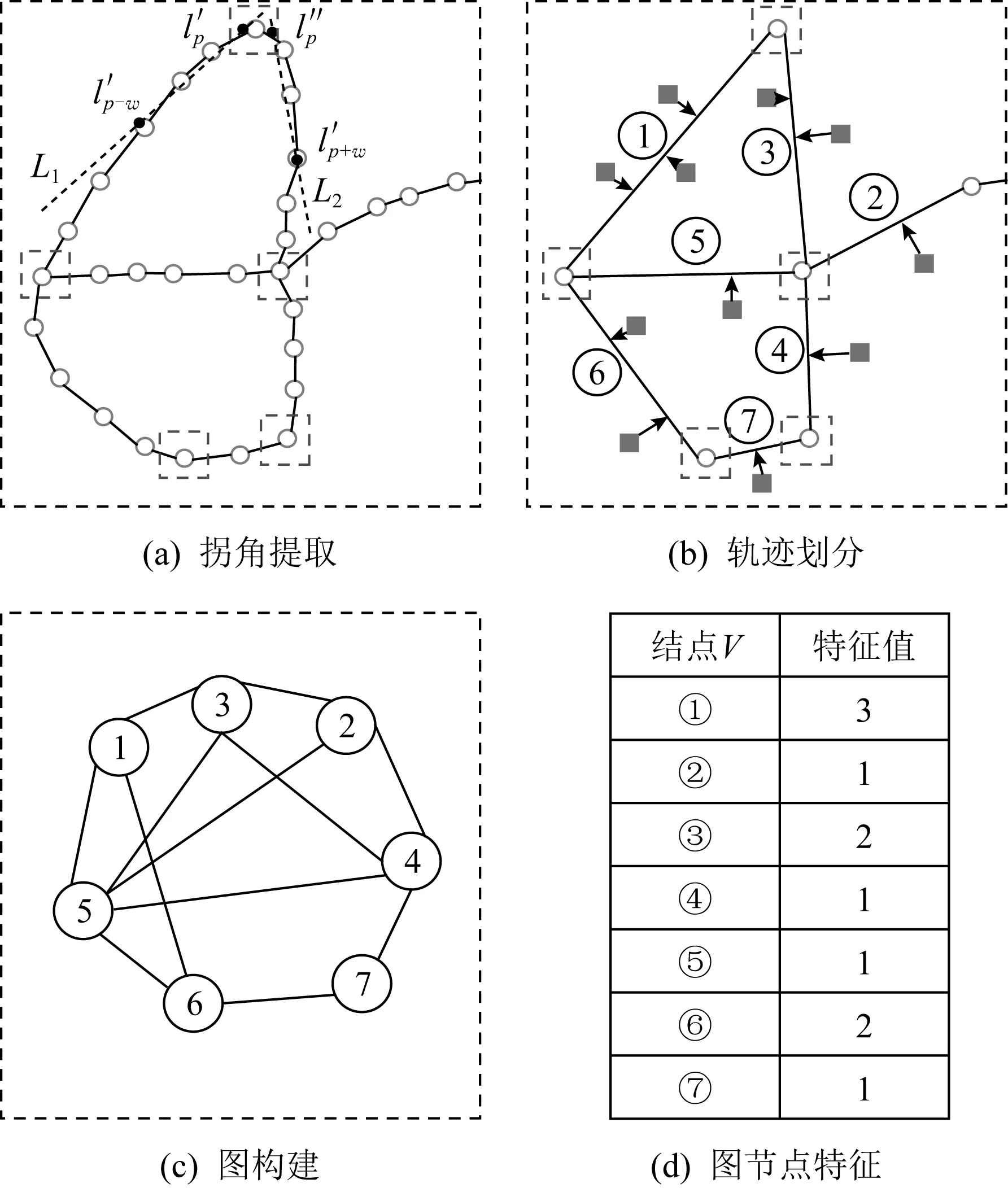
Fig. 2 The process of graph construction圖2 圖構建過程

2) 構建軌跡圖.由上述步驟得到的道路網絡結構無法以矩陣和向量形式表達，很難以傳統的神經網絡模型來捕捉各個路段的空間依賴關系，故使用這些路段構建圖

G

=(

V

,

E

)，以圖的形式來存儲軌跡信息

.

圖

G

中的

V

為結點集，將軌跡聚類后得到的每一條軌跡視作一個結點，故軌跡的個數就是圖

G

中結點的個數；

E

為邊集，如果2條軌跡間有連接，則兩結點間就有邊.圖使用鄰接矩陣和特征矩陣存儲.鄰接矩陣表示各結點間的連接關系，鄰接矩陣的值為0或1，如果兩結點之間有連接則為1，反之則為0.特征矩陣包含各結點代表路段的特征信息，數據空間中眾包任務視作發生在最近的軌跡路段，

p

時結點的特征值為

p

時內軌跡路段上發生的任務數量.圖2(b)圖所示的軌跡被5個拐點劃分為7條路段，分別被標記為①～⑦，方塊代表空間眾包任務.最終生成的圖結構如圖2(c)所示，將各任務劃分到距離最近的軌跡路段上，可得到各結點的特征值如圖2(d)表格所示.如果圖有很多結點的特征長時間為0的結點，會影響模型的效果.為提高模型預測的效果，在每一時間段篩選掉任務發布數低于閾值的軌跡路段，將這些軌跡代表的結點從該時段中刪除.

3.2 基于圖卷積的任務分布預測模型

本節將基于3.1節得到的圖結構數據通過基于圖卷積的任務分布預測模型來預測路段的流量，再使用核密度估計的方法預測各路段任務發生的具體位置，最后給出了預測要發生價值的方法.具體為如下3個步驟：

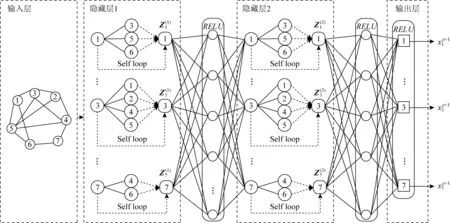
Fig. 3 Prediction model of task distribution圖3 任務分布預測模型

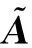
(3)

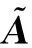
(4)

=

ReLU

(·

ReLU

(··)·),

(5)

(

u

=1,2,…,

k

),

(6)

(

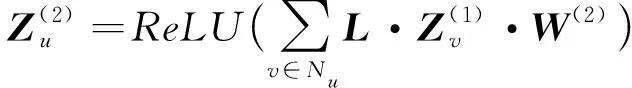
u

=1,2,…,

k

),

(7)

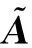
h

={

R

(

K

)}(15)

/

{

m

(

K

)}(25)

R

(

f

″)(15)

n

(15),

(8)

截選圖3(b)中的軌跡路段①如圖4(a)所示，軌跡①在歷史上有3個任務發生，將這些任務投影到路段①上，可以得到3個投影點的坐標為

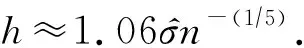
l

,

l

,

l

.

使用核密度估計函數

f

計算可以得到任務發生位置的概率密度函數

f

(

x

) 如圖4(b)所示

.

假設預測得到下一時刻任務發布的數量為

m

，路段從上至下的兩側的端點坐標為(

x

,

y

)、(

x

,

y

)，概率密度函數

f

(

x

)前

m

高的橫坐標集合

X

={

x

,

x

,…,

x

,

x

+1,…,

x

}，則預測得到的

m

個任務發布坐標(

x

,

y

)可通過式(10)得到：

(9)

(

x

,

y

)=

(10)

其中，

d

為軌跡路段的長度，(

x

,

y

)和(

x

,

y

)分別表示軌跡路段左端點和右端點的坐標，

d

由軌跡路段兩端的坐標求歐氏距離計算；(

x

,

y

)為軌跡路段上預測得到的第

i

個點的坐標，

i

的取值為1到

m.

Fig. 4 Diagram of specific location prediction of task publishing圖4 任務發布具體位置預測示意圖

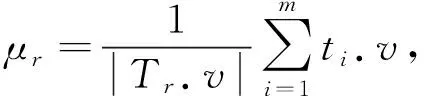
(11)

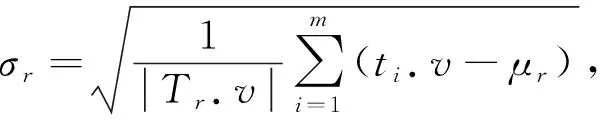
(12)

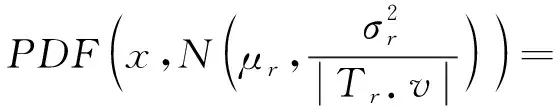
(13)

任務價值的預估可分為如下3種情況：

(14)

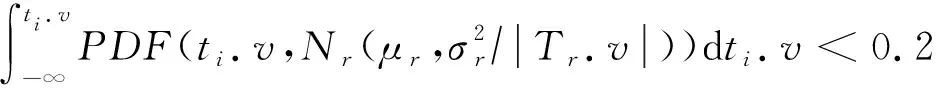
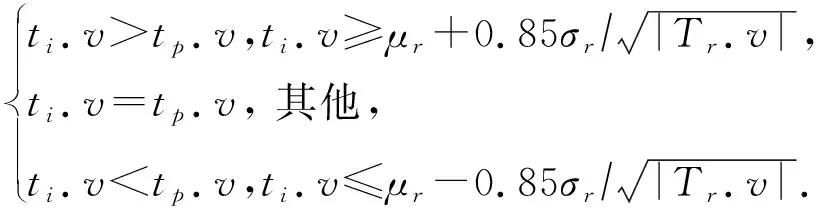
(15)

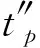
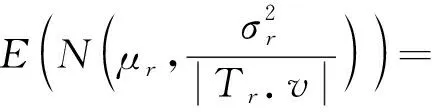
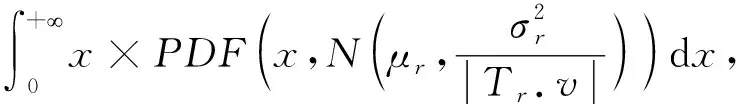
(16)

(17)

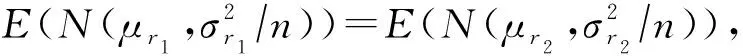
4 基于核密度估計的工人分布預測模型

由于空間眾包系統中工人位置信息的強時效性，為了實現全局更優的分配，需要對新加入空間眾包系統的工人的位置信息進行精確預測.本節將介紹一種基于ConvLSTM的工人簽到位置預測方法，它可以有效地估計未來時刻工人的數量和位置分布.工人分布預測過程的總體結構圖如圖5所示，從左向右，首先通過二維核密度估計進行過去時間工人簽到位置分布平滑化處理，使得ConvLSTM模塊可以更容易地提取到空間分布的特征.然后，構建基于ConvLSTM的2層網絡模型，在輸入層按照定寬的窗口滑動劃分各時刻的二維核密度估計矩陣，得到時序的核密度估計矩陣投入模型，經過隱藏層的ConvLSTM模塊提取空間特征，接著通過輸出層預測得到下一時刻的工人分布的二維核密度估計矩陣.最后，通過刪減策略的數量還原過程來精確預測未來時刻工人位置的分布.

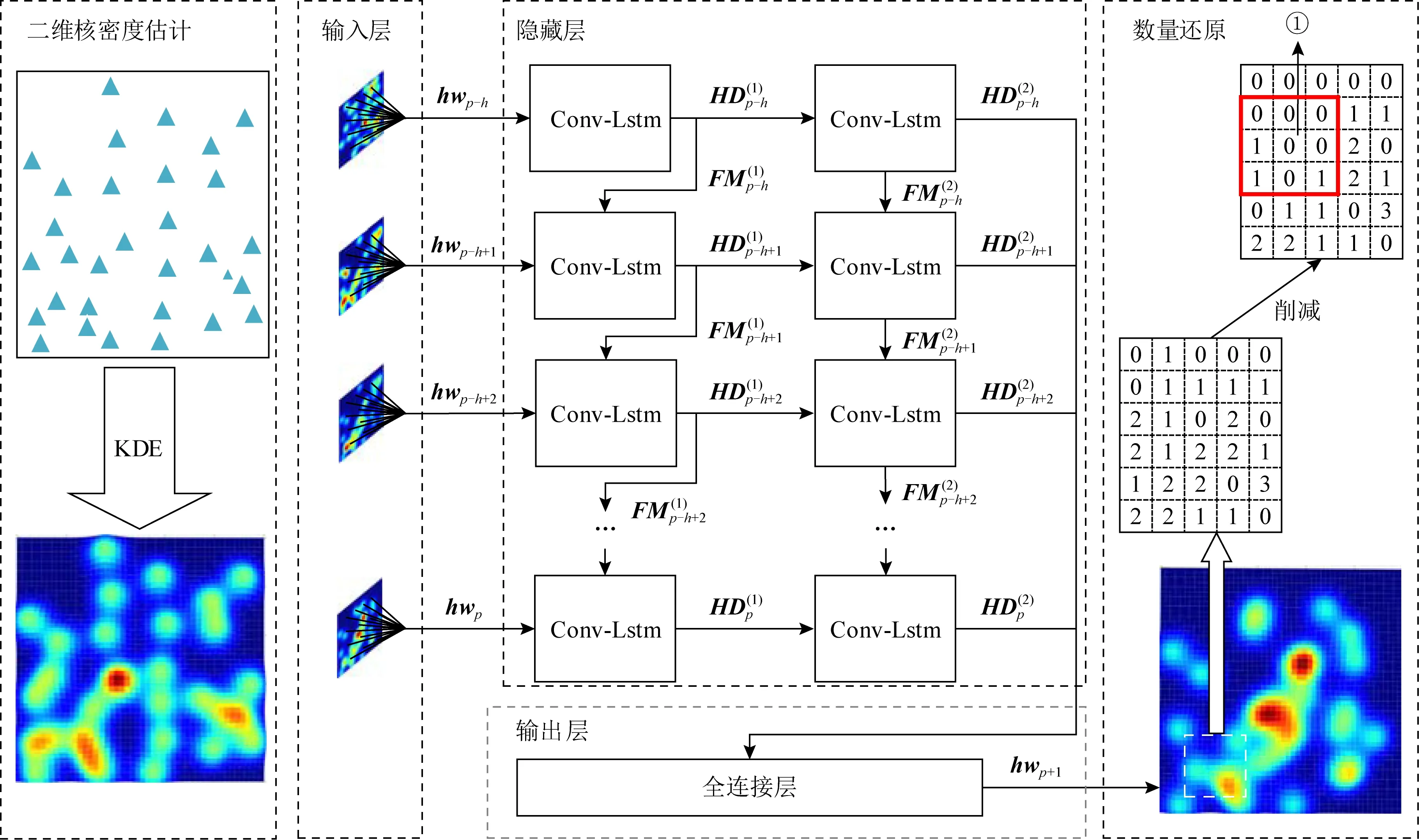
Fig. 5 Working mechanism of worker distribution prediction圖5 工人分布預測工作原理

4.1 二維核密度估計位置分布

本節將任務的位置分布信息使用其二維核密度圖進行表示

.

將真實世界的地圖視作一個

U

=[0,1]的二維數據空間，對于每個時間實例的工人簽到位置分布樣本，使用二維核密度估計可以得到工人分布的概率分布曲線

.

對數據空間

U

中的概率分布曲線進行模擬，數據空間二維長度均為0到1，如果不對估計函數歸一化處理，數據空間中對應位置的函數值就是該位置可能簽到的工人數量

.

二維核密度的估計函數為

K

((

x

[

dim

]-

x

[

dim

])

/H

)，其中，

K

(·)為核函數，

dim

表示維度(

dim

=1表示二維數據空間的第一維)，由于后續分配工人時會對核密度估計矩陣進行向下取整的操作，為避免向下取整丟失較大的小數值(比如1

.

9取整為1)此處使用均勻核函數

K

(

x

)=1

/

2，-1≤

x

≤1，

H

為平滑參數帶寬，計算方法與3

.

1節中計算核密度估計滑窗的方法類似(

H

，

H

需要分別計算)

.

通過如圖5所示方法可以得到工人的分布矩陣，該步驟如圖5中二維核密度估計部分所示，得到的分布矩陣類似圖中的熱力圖，核密度估計將稀疏的樣本通過帶寬

H

擴散到相鄰區域，使得工人分布矩陣密度變高，方便后續卷積過程更好地捕捉工人空間分布的特征

.

但也是由于該原因，工人矩陣中的數量和并不是真正的工人數量

.

4.2 基于ConvLSTM的工人分布預測模型

本節將通過工人分布預測模型提取工人分布核密度估計矩陣的時空特征來預測下一時刻的工人分布，并基于核密度估計原理復原真實工人數量，具體分為如下2個步驟：

1) 工人預測模型網絡結構.由于ConvLSTM模型在時空數據特征提取上性能較佳，本文將其應用于預測眾包工人登錄位置分布.在ConvLSTM中，要預測時間實例

p

+1時的工人位置分布，需要基于設定的滑窗寬度

s

輸入一組過去工人分布的核密度估計矩陣的時間序列

H

={-,-+1,…,-1,}，

H

表示核密度估計矩陣的時間序列，為時刻

p

的核密度估計矩陣

.

時間序列

H

為圖5中輸入層的輸入

.

網絡結構中各參數的形式化表達如式(18)～(23)所示：=

Sigmoid

(

Conv

(;)+

Conv

(-1;)+),

(18)

=

Sigmoid

(

Conv

(;)+

Conv

(-1;)+),

(19)

=

Sigmoid

(

Conv

(;)+

Conv

(-1;)+),

(20)

=Tanh(

Conv

(;)+

Conv

(-1;)+),

(21)

=⊙-1+⊙,

(22)

=⊙Tanh(),

(23)

其中，⊙符號表示矩陣的哈達瑪乘積，,,分別表示輸入門、遺忘門、輸出門3個門的程度參數，是常規循環神經網絡(recurrent neural network, RNN)步驟得到的特征，為短時記憶，表示長時記憶，

/

分別為輸出給下一單元

/

最后輸出的特征

.

在隱藏層網絡中，如圖5隱藏層部分，各ConvLSTM單元的長期記憶隨著輸入序列時間方向傳播，各單元的輸出隨網絡的深度方向傳播

.

經過2層網絡提取的時空特征，輸出結果經圖5中輸出層的全連接網絡后，可以預測得到

p

+1時刻的工人分布核密度估計矩陣+1

.

2) 復原真實工人數量

.

通過上述步驟預測得的工人分布核密度估計矩陣+1是

p

+1時刻工人分布的核密度估計矩陣，分配工人前需要先對矩陣進行取整操作

.

根據核密度估計的原理，核密度估計矩陣是通過核函數

K

(·)以帶寬

H

對每一個樣本進行觀察，并擬合樣本點附近的概率，將所有的概率密度函數合并得到的，故每個樣本影響概率分布的范圍為±

H

.

所以，核密度估計矩陣中對應位置的值并不是真實工人數量，若要得到+1中的真實工人數量，需要在減少矩陣某位置的數量時，同時減少該位置±

H

范圍的值

.

復原真實工人數量方法如下：假設核密度估計時使用的

H

為矩陣的

len

個寬度，如果分配矩陣中(

i

,

j

)位置的一個工人，需要將(

i

,

j

)位置和{

i

-

len

,…,

i

,…,

i

+

len

}?{

j

-

len

,…,

j

,…,

j

+

len

} (?表示笛卡爾積)中元素位置中工人數量大于零的部分全部減少1

.

以圖5中數量復原部分使用虛線框截取矩陣中的一部分為例，箭頭連接的矩陣為該部分工人的分布矩陣，矩陣中的數字表示對應位置的工人數量

.

通過模擬分配2個工人的過程來展示消減數量策略的過程，如圖6所示: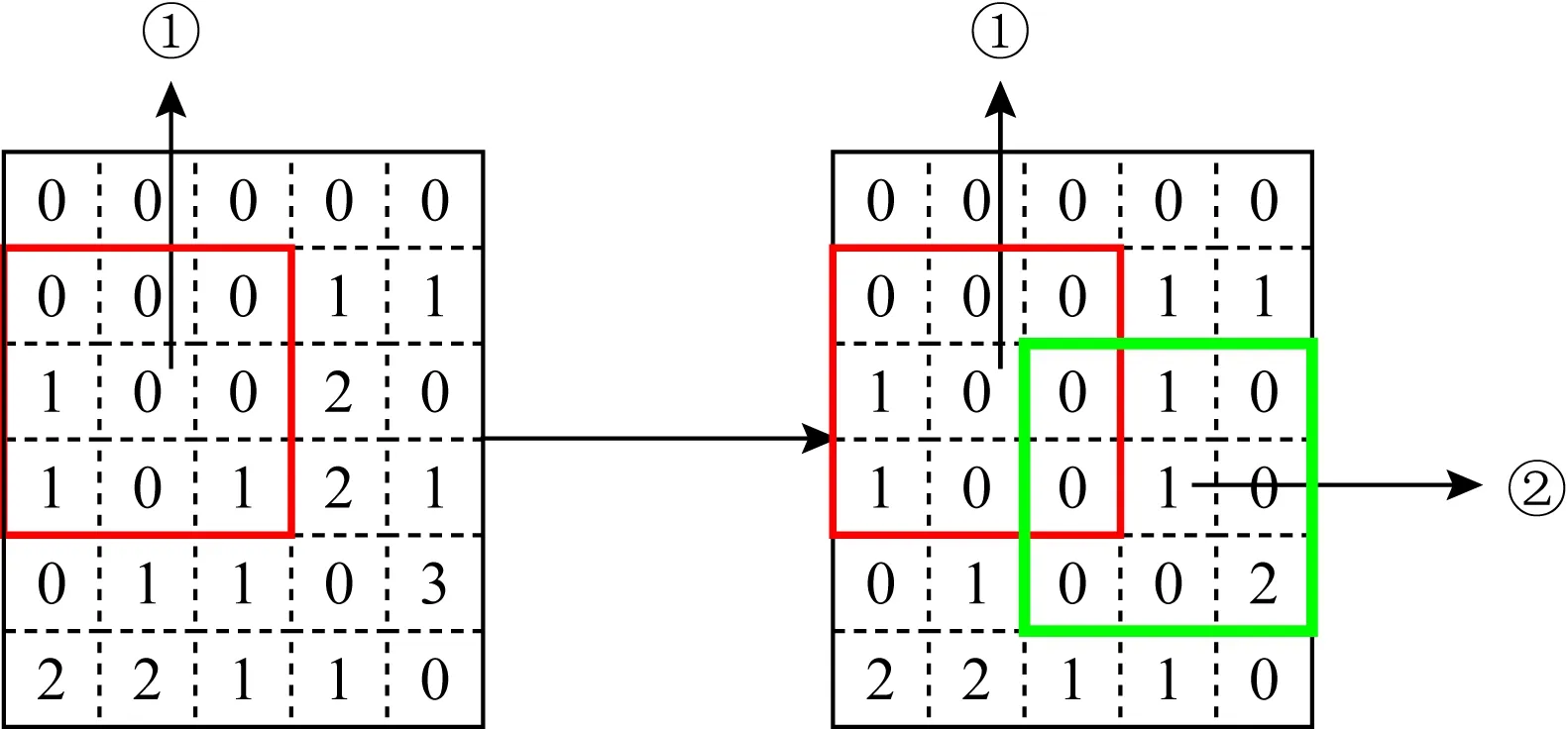

Fig. 6 Example of quantity reduction圖6 數量削減過程示例

首先，將圖6中標注①的(3,2)位置處的1個工人進行分配，假設進行核密度估計時計算出的

H

在核密度估計矩陣中寬度為1，則以集合{2,3,4}?{1,2,3}={(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3)}的九宮格內，數量大于零的位置工人數量均要減少1；將標注②的(4,4)位置處的1個工人進行分配，矩陣中{3,4,5}?{3,4,5}={(3,3),(3,4),(3,5),(4,3),(4,4),(4,5),(5,3),(5,4),(5,5)}位置的網格中人數均減1

.

分配可以持續到矩陣所有位置的數量都為0

.

5 基于位置預測的任務分配算法

傳統的任務分配問題一般可視為最大流問題，本文提出的最大價值最小成本任務分配問題可以分類為一種包含位置預測數據，任務為結點和工人為權值的二分圖最大流問題，并且結點和邊均帶權值.解決最大流問題的傳統算法有匈牙利算法和Kuhn-Munkras算法，若圖中結點有|

V

|個，邊有|

E

|個，則前者的時間復雜度為

O

(|

V

|×|

E

|)，但不能解決帶權值的二分圖最大流問題，后者可以解決帶權值的二分圖最大流問題，但時間復雜度為

O

(|

V

|)，難以應用于現實場景.傳統的方法沒有完全適配本文問題的求解方法.故本節提出一種基于貪心算法和匈牙利算法的啟發式算法，通過搜索任務的可用工人集，構造二分圖，盡可能尋找符合目標函數式(1)(2)的最優分配.

定義4.

任務可用工人集

.

在理想的眾包系統中，每個空間任務的有效工人集由任務需要的技能和工人擁有的技能、工人的可信度等幾個因素決定，但現有的數據集中缺少這幾種屬性，故本實驗中僅考慮工人是否可以在任務結束前到達任務位置(不考慮工人執行任務的時間)

.

在

p

時，若已存在系統中和預測將要加入系統的空間任務和眾包工人分別有

M

和

N

個，空間任務

t

的可用工人集表示為

AW

，且應該遵循以下條件：?

w

∈

AW

,1)

dist

(

t

,

w

)≤(

t.e

-

p

)×

w.v

；

其中，

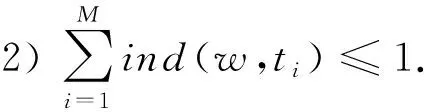
ind

(

w

,

t

)表示一個指示器，若工人

w

被分配給任務

t

，則

ind

(

w

,

t

)=1，否則

ind

(

w

,

t

)=0；

dist

(

t

,

w

)為任務位置

t

.l

到工人位置

w

.l

之間的歐氏距離，若任務

t

為預測得到的任務，則任務位置

t

.l

為式(4)計算得到的坐標(

x

,

y

)，若工人

w

為預測得到的任務，則任務

j

的位置

w

.l

為任務

j

所在核密度矩陣位置對應網格處的中心坐標

.

5.1 基于預測數據的任務分配算法

假設時間序列

P

中系統中一共存在任務及工人分別有

M

和

N

個，算法目的為在多項式時間復雜度內將

N

個工人分配給

M

個任務，并使分配對間的平均移動距離盡可能低，分配對的總價值盡可能高

.

算法1給出基于預測數據的任務分配算法的偽代碼

.

算法1.

基于預測數據的任務分配算法.輸入：時間序列

P

={1,2,…,

p

,…}、時刻

p

任務集

T

、時刻

p

工人集

W

；輸出：任務分配集

I.

② for

p

=1 to

n

then③

T

←

T

+

T

,

W

←

W

+

W

,

T

←?,

W

←?;④

I

←?,

W

←?,

T

←?,

C

←?;

⑥ if 分配對〈

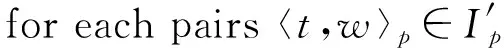
t

,

w

〉在時刻

p

存在 then⑦

I

←

I

+〈

t

,

w

〉;⑧ else 將已有的對象加入

T

或

W

;

⑨ end if

⑩ end for

i

←-1;

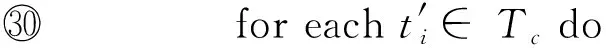
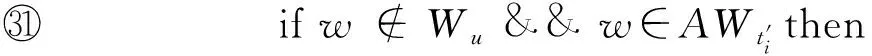
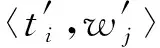
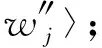
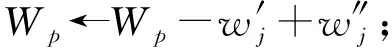
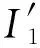
5.2 算法復雜性分析

本文算法中生成所有

AW

的復雜度約為

O

(

N

×

M

)，分配步驟的復雜度約為

O

(

M

×log

M

+

M

×

N

×log

N

)，故從整體的角度分析其平均時間復雜度約為

O

(

N

×

M

×log

M

)，此處

N

表示工人的數量，

M

為任務的數量

.

Fig. 7 Example of task assignment圖7 任務分配示例

例1.

如圖7所示，共有4個任務(

t

～

t

)和5個工人(

w

～

w

)，任務的價值和工人到各任務的距離如表1和表2所示

.

首先分配價值較高的空間任務

t

，在

t

的可用工人集中，距離最近的是工人

w

，故首先將

w

分配給

t

.

然后分配價值為4的空間任務

t

，在

t

的可用工人集中，距離最近的是工人

w

，并且

w

沒有分配給別的任務，故把

w

分配給任務

t

.

接著分配任務

t

，

t

可用的工人中距離最近的工人是

w

，故將

w

分配給任務

t

.

最后分配

t

，

t

的可用工人

w

和

w

均已經被分配，故可以得出沖突任務集

T

為{〈

t

,

w

〉,〈

t

,

w

〉}，兩沖突分配對的距離分別為2和4，首先嘗試替換

t

的分配，但

t

沒有其他可用工人，故選擇替換〈

t

,

w

〉為〈

t

,

w

〉

.

最終得到的分配

I

={〈

t

,

w

〉,〈

t

,

w

〉,〈

t

,

w

〉,〈

t

,

w

〉}，而剩余無法被分配的

w

會留到下一時刻繼續參與分配

.

經過本文方法分配后，得到的總價值為14，平均距離為2

.

75；而從價值高的任務開始遍歷，每次選取距離最近工人的貪心法取得的總價值12，平均距離為3，14>12且2

.

75<3，本文的方法明顯更優

.

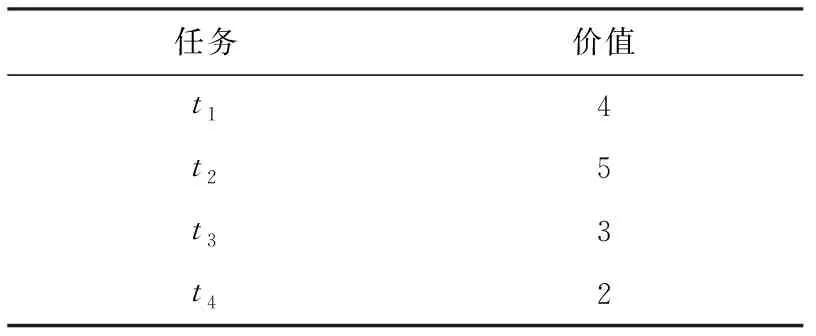
Table 1 Task Value

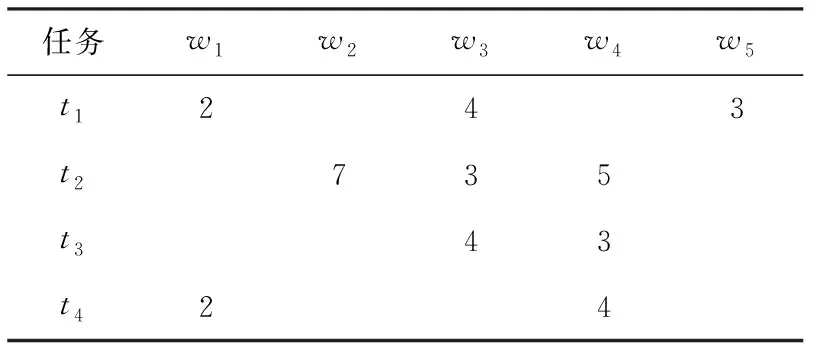
Table 2 Distance of Task and Worker

6 實 驗

6.1 實驗設置

本文實驗部分使用滴滴蓋亞開放數據計劃提供的真實數據集，具體在滴滴提供的KDD CUP 2020網約車數據集上測試提出的算法.該數據集中包含30天的用戶訂單數據和司機軌跡數據，共有7 065 937個訂單數據，來自1 181 180個司機的6 105 003條軌跡數據，數據均來自滴滴公司的網約車服務.本實驗以該數據集范圍內的區域(經度104.042 102°～104.129 591°和緯度30.652 828°～30.727 818°范圍內的區域)作為實驗的背景地區.實驗將訂單數據和司機軌跡數據分別視作最大價值最小成本任務分配問題中的空間任務和眾包工人，具體地說，訂單的發布時間視作空間任務的發布時間，訂單的發布位置視作空間任務的發布位置，訂單價值視作空間任務的價值；將每條軌跡的首個時間戳和首個軌跡點坐標視作一個眾包工人的登錄時間戳和登錄位置.經過處理得到的數據集包含7 065 937個眾包任務和6 105 003個眾包工人.

本實驗在該數據集上通過3.1節的軌跡聚類得到315個拐角和384條軌跡，經過圖構建過程建立出一個384個結點，806條邊的圖(根據各路段間的連接情況得到).為驗證所提方法的性能，對最大價值最小成本任務分配問題中需要但數據集里不存在的屬性進行合成，本實驗使用高斯分布來模擬每個任務的持續時間和工人的速度，此處任務持續時間指的是任務發布后的有效時間，也就是

t.e

-

p

，工人速度指的是工人的移動速度，也就是

w.v.

如表3所示，任務持續時間和工人移動速度在

N

((

p

+

p

)

/

2,(

p

-

p

))和

N

((

v

+

v

)

/

2,(

v

-

v

))中隨機取值

.

實驗中選擇前20天的數據作為訓練集，第21天的數據作為驗證集，22～30天的數據作為測試集

.

Table 3 Experimental Parameters

6.2 評價標準及對比算法

本實驗根據預測結果的準確率以及誤差來評估本文預測方法的有效性；以式(1)中定義的最大化總分配價值和式(2)最小化分配中工人到空間任務的平均距離目標，衡量分配策略的質量，并以最小化計算所消耗的CPU時間為目標，來衡量分配策略的效率.表3給出本文的實驗參數設置，其中默認值以黑體顯示.在實驗過程中，每組實驗都會改變一個參數，其他參數均會設置為默認值.

在本文的實驗中，任務預測方法的有效性驗證采取2種對比方法：1)單層圖卷積網絡(GCN-α).該方法使用本文3.2節中去掉隱藏層2的任務位置預測模型進行預測；2)基于網格的任務預測方法(grid-based task prediction, GTP).使用基于網格劃分的方法劃分數據空間，并在各單元格內使用線性回歸的方法進行任務數量預測，并假設任務發生在單元格的中心位置.工人位置預測方法的有效性驗證采取2種對比方法：1)不使用核密度估計處理工人分布圖的ConvLSTM模型(ConvLSTM-α).該方法為本文的基于ConvLSTM的工人分布預測模型，去掉4.1節和4.2節(2)中二維核密度估計預處理和還原步驟的工人位置預測模型；2)基于網格的任務預測法(grid-based worker prediction, GWP).與GWP相似，網格劃分數據空間，使用線性回歸法進行工人數量預測.

分配方法的有效性和效率采用了2種基礎的對比算法：1)貪心分配算法(greedy).以任務價值從高到低的順序選擇任務，每個任務均在其可用工人集中選擇距離最短的工人進行分配，若沒有可用工人集，則該任務當前時間實例無法分配.與本文基于預測數據的任務分配算法相比較，貪心分配算法把其中分配部分替換為貪心算法，平均時間復雜度約為

O

(2

M

×

N

+

M

×log

M

).2)隨機分配算法(random).隨機選擇一個任務，在其可用工人集中隨機選擇工人進行分配，若沒有可用工人集，則該任務當前時間實例無法分配，該分配算法的平均復雜度約為

O

(

M

×

N

+

M

)，其中

M

為任務數量，

N

為工人數量.

本文所有實驗均是在AMD Ryzen 5 3600 CPU@3.6 GHz,16 GB內存以及Nvidia GTX 1660s硬件條件下使用Python語言實現實驗中算法.

6.3 工人和任務預測效果分析

本節實驗對工人預測效果表現進行評估，并評估其對后續任務分配步驟的影響.使用前20天的數據作為訓練集，后9天為測試集，并通過改變滑窗寬度和訓練集大小，來測試模型準確度的變化，同時設定模型的其他參數如表3中默認值(加黑)所示 .

1) 滑窗寬度的影響.

首先通過改變滑窗寬度來評估工人和任務分布預測的準確性，實驗的epoch設置均為100，分別使用平均絕對誤差(mean absolute error, MAE)和均方根誤差(root mean square error, RSME)2種誤差來衡量模型的準確度情況，滑動窗口帶寬的取值為4，6，8，10，12.如圖8(a)～(b)所示，對于任務分布預測模型，可以觀察到隨著滑窗寬度從4增大到8的過程中，預測的誤差略有下降，但從8增大到12的這個過程中，預測的誤差基本上停止變化.這是因為在3.2節對任務預測的模型設定中，滑窗寬度代表投入模型的歷史數據量大小.3.1節中基于時間劃分不同模型一定程度上消除任務位置分布隨時間變化的影響，對于任務位置預測模型來說不需要太多的歷史數據進行學習.圖8(c)～(d)中工人分布預測中滑窗寬度從8增大到12的過程中，誤差反而有所增加，這是因為工人的分布隨時間變化較為迅速，使用較多的歷史數據反而會導致模型不能專注于近期的變化，產生較大的誤差.總的來說，2個模型對于帶寬的敏感程度都不大，且預測效果均較好(MAE和RMSE均小于1)，根據實驗結果選擇默認的滑動窗口大小為8.

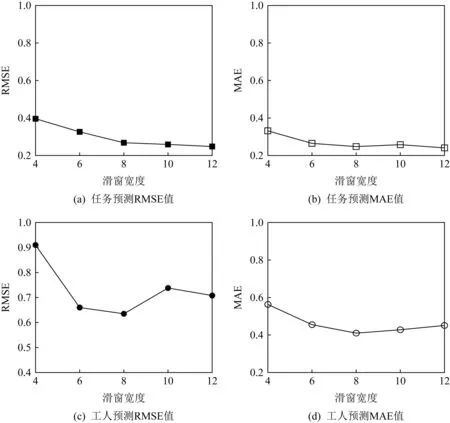
Fig. 8 Task/worker prediction model effect圖8 任務/工人預測模型效果

2) 訓練集大小的影響.

① 任務分布預測分析.通過改變訓練集大小來評估工人位置預測算法的性能和該部分對后續任務分配的影響.數據集的前20天設定為訓練集，訓練集的大小取值為30%，40%，60%，80%，100%.對于任務位置分布預測，使用了2種對比方法：基于網格的任務預測方法(GTP)，單層圖卷積網絡(GCN-α).為衡量模型性能，使用一種基于網格的準確率：將二維數據空間分為等大小的網格，通過比較單元中工作者/任務的估計數量

q

′和實際數

q

得出準確率

ACC

=|

q

′-

q

|

/q

×100%.為了測試位置預測效果對分配結果的影響，使用本文所提基于位置預測的任務分配算法，基于位置預測進行了任務分配，并計算了分配的總價值.

在準確率評估實驗中，在圖9(a)中可以觀察到，隨著訓練集變大，3種方法均有一定程度的準確率提升.本文方法的準確率從64.4%提升到了89.1%，比排名第2的GCN-α最終的82.1%高出了7個百分點，而GTP方法的準確率最后穩定在73.5%左右.在圖9(b)中可以發現分配得到的價值隨著3種方法準確率的增加均有明顯上升.GCN-α和GTP方法在訓練集從40%增加到60%的步驟中有較大的價值提升，這是因為訓練集大小在30%～40%左右時，GCN-α和GTP的準確率僅有50%左右，導致產生了大量無效分配，在準確率提高后分配效果才有所提升.而本文方法的準確穩定在64%以上，故總的分配價值比較穩定.本文方法在3種方法中表現最好，原因在于本文方法使用軌跡路段作為預測任務分布的基礎，相較GTP和GCN-α預測方法更加精細，更加符合工人接受任務的位置.

② 工人分布預測分析.對于工人的位置分布預測，對比本文方法選擇了2種對比方法：基于網格的工人預測方法(GWP)，不進行二維核密度估計的本文方法(ConvLSTM-α) .為了衡量模型性能，同樣使用

ACC

=|

q

′-

q

|

/q

×100%做為準確率評價標準，與任務預測算法效果實驗中相似，使用基于位置預測的任務分配算法進行任務分配，并比較分配的總價值.

準確率評估實驗如圖10(a)所示，隨著訓練集增大，3種方法工人預測的準確率均有的增加.本文方法準確率最高，其次是GWP和ConvLSTM-α.原因在于本文方法通過核密度估計把數據空間劃分為比GWP方法更精細的子區域，使用核密度估計彌補了工人分布矩陣的稀疏性，相較ConvLSTM-α方法中直接使用ConvLSTM提取時空特征的做法，可以更好的提取工人分布的空間特征.本文方法工人預測準確率最高可達73.6%，相比GWP方法高出18.8個百分點.ConvLSTM-α方法的準確率最終僅達到52.3%，這是由于沒有經過預處理的工人分布圖過于稀疏，模型不能提取到空間特征，導致預測結果不理想.圖10(b)中，在訓練集大小從30%增加到40%的過程中可以觀察到基于ConvLSTM-α方法預測的分配結果反而有所下降，這是由于任務分配很大程度上依賴位置預測的結果，而ConvLSTM-α預測結果平均準確度僅有21%，較差的預測準確率會使分配得到的價值不穩定.

Fig. 9 Performance comparison of task prediction under different training sets圖9 不同訓練集下任務預測性能對比

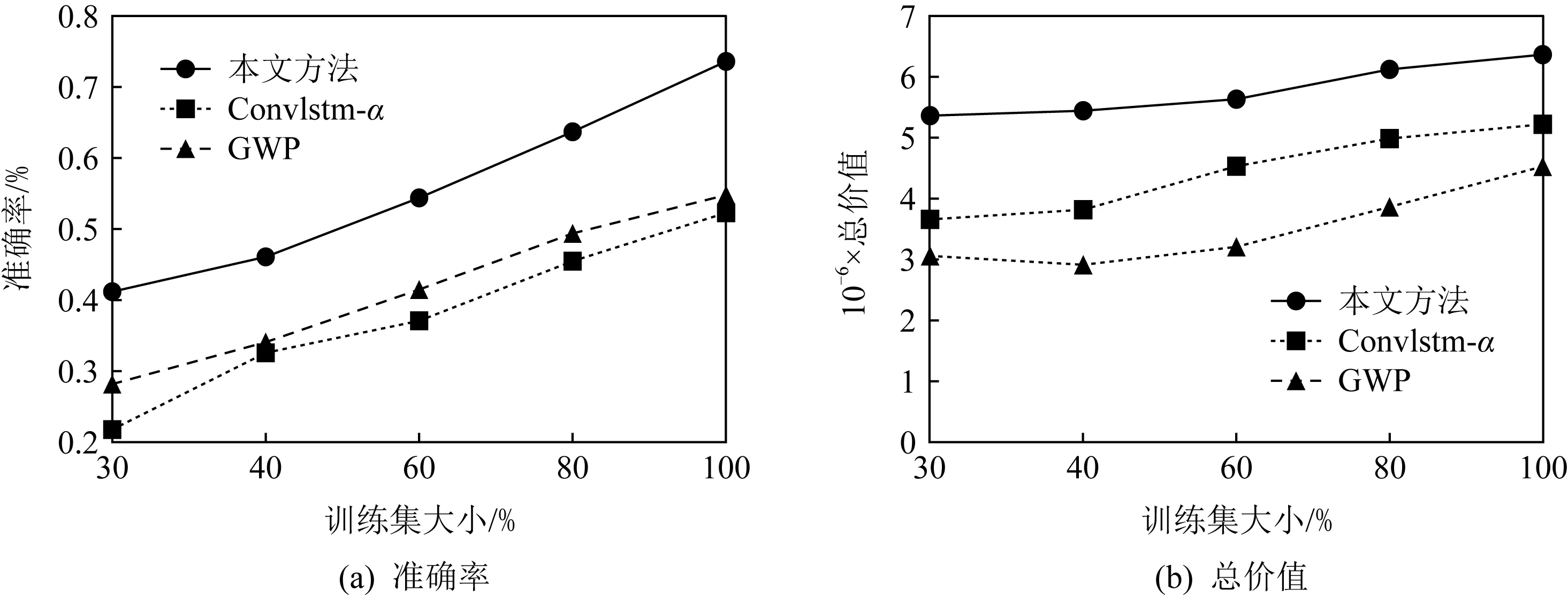
Fig. 10 Performance comparison of worker prediction under different training sets圖10 不同訓練集下工人預測性能對比

6.4 任務分配效果分析

本節實驗評估本文提出的基于位置預測的任務分配算法的有效性，本節使用任務分配的總價值和分配對任務/工人間的平均距離評價分配策略的效果，使用計算分配所需的CPU時間評價分配策略的效率.對比算法選擇貪心分配算法(Greedy)和隨機分配算法(Random).除了2種基礎的對比算法，還實現了3種樸素對比算法，即3種預測算法不使用位置預測數據，在僅考慮當前時刻任務/工人分布的情況下進行分配.對比算法分別為：基于位置預測的任務分配算法(本文方法)、貪心分配算法(Greedy)、隨機分配算法(Random)，和不加位置預測的任務分配算法(本文方法-α)、不加預測的貪心分配算法(Greedy-α)、不加預測的隨機分配算法(Random-α).

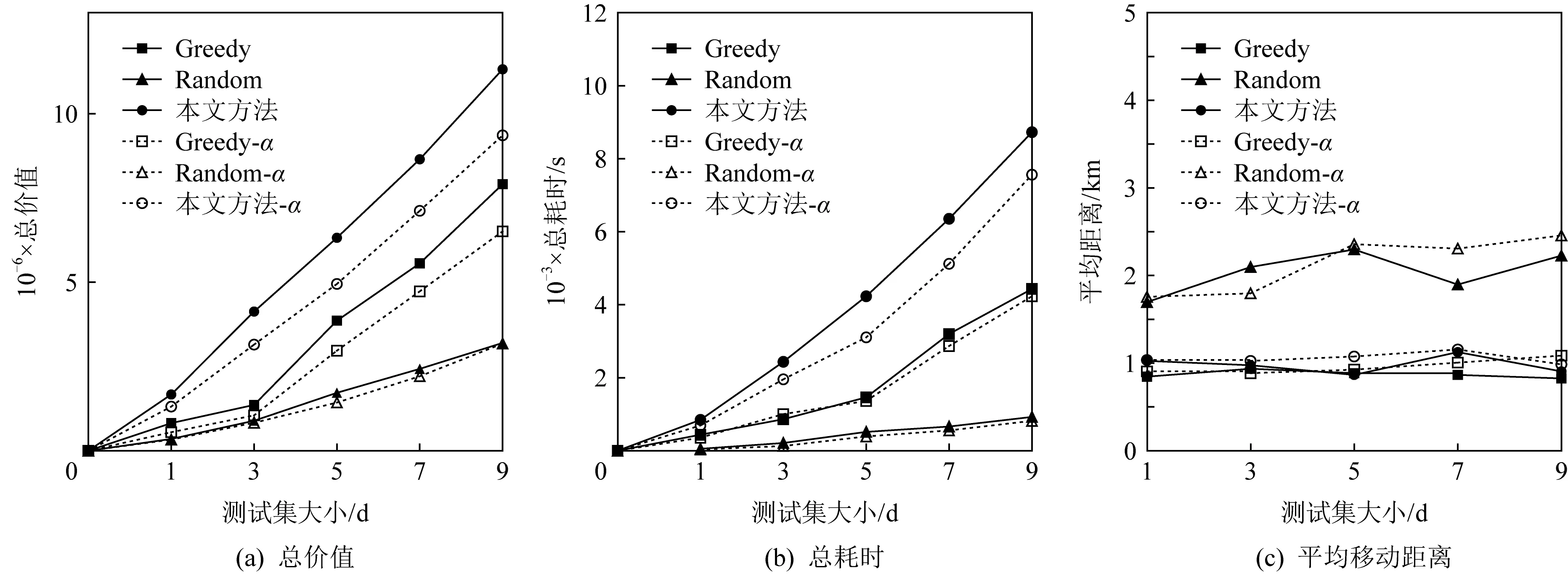
Fig. 11 Comparison of task assignment performance under different datasets圖11 不同測試集下任務分配性能對比

1) 測試集大小的影響.實驗選擇22～30天的數據作為測試集，訓練集大小取值分別為1天，3天，5天，7天，9天.首先改變測試集的大小來研究分配算法的性能和時間效率，也即通過改變參加分配的任務和工人數量來測試算法.價值評估實驗如圖11(a) 所示，所有算法分配得的總價值隨著測試集大小的增加而增長；同時可以觀察到Random算法和Random-α算法計算得到的分配總價值最低，而本文提出任務分配算法得到的分配總價值最高，隨后是本文方法-α、Greedy和Greedy-α，這是由于本文方法在有任務無法被分配時，會考慮替換已有的分配實現更好的分配組合.總體上講，所有使用了位置預測算法效果均要比沒有使用預測的算法好，這是由于基于位置預測的分配算法從全局的角度進行了分配.而Random-α在一些情況下優于Random算法是由于隨機分配算法有較強的隨機性，實驗結果均符合預期.圖11(b)所示為各算法時間對比，該部分統計的CPU時間是分配所消耗的總時間.隨著訓練集的增大，各算法計算所用時間均呈線性增長，因為3種算法的時間復雜度均與任務/工人數量相關，任務/工人數量的增加導致耗時增加.可以觀察到所有使用位置預測的算法時間消耗均高于不使用預測的算法，這是因為預測數據本身需要消耗時間，且預測得到的任務/工人也參與分配增加了3種算法要分配的任務數量.本文方法的耗時最高，這是尋找盡可能多的分配對需要消耗時間.圖11(c)為各分配對間的任務和工人間的平均距離變化情況.隨著訓練集大小的增長，Greedy算法和本文提出的任務分配算法的變化較為穩定，基于位置預測的分配平均距離與不考慮位置預測的平均據接近，同樣穩定.但Random算法的平均距離并不穩定，這是因為隨機分配有較強的隨機性，這種分配結果顯然效果較差，真實的空間眾包平臺中工人的移動距離必然是越短越穩定越好.Greedy算法和本文方法的平均距離接近，但Greedy算法的效果略優，這是因為Greedy算法為每個任務都分配了最近的工人，而本文方法為了分配更多的任務，選擇將一些工人分配給了較遠的任務，這也是本文方法總分配價值遠高于Greedy算法的原因.

2) 任務持續時間的影響.接下來通過改變任務持續時間測試分配方法的效果和效率，任務持續時間為高斯分布[

p

,

p

]區間內隨機取值.如圖12(a)所示，隨著任務持續時間的增長，所有方法的分配總價值均有增長，這是由于任務有更長的持續時間意味著原本無法被分配任務可以在更多的時間實例參與分配，使該任務更可能得到分配.本文分配方法同樣取得了最高的總價值，所有含位置預測的分配方法均要優于不含位置預測的分配算法，可以證明本文方法的可行性，和預測方法的有效性.圖12(b)中統計的耗時為進行一個時刻任務分配消耗的CPU時間.可以觀察到，隨著任務持續時間的增加，所有方法的計算分配所需的時間都有所增長，這是因為任務的持續時間增長，導致任務的可用工人集變大，而分配算法的時間復雜度與可用工人集大小也有關，與預期結果相符.在最極端的情況下本文方法平均耗時也僅高于Random算法4.20 s，屬于可以接受的范圍.從圖12(c)中可以觀察到除Random算法外各算法的平均距離均較為穩定，同樣證明了本文方法的可行性.3) 工人移動速度的影響.實驗通過改變工人移動速度測試分配方法的效果和效率，工人移動速度為高斯分布[

v

,

v

]區間內隨機取值.圖13(a)中，隨著工人移動速度增加，所有方法得到的分配總價值均有增長，原因與任務持續時間增長帶來的影響類似.工人移動速度增加相等于增加了每個任務的可用工人集，而所有的分配算法均是在可用工人集上進行的，更多的可用工人可能讓原本無法被分配的任務更可能得到分配，同樣這增加了需要計算的任務/工人數量，導致了圖13(b)中Random算法外所有算法的耗時均有明顯增加.圖13(c)所示本文分配算法計算得的工人平均移動距離依舊穩定.本文方法僅比Random算法平均多耗時僅為4.89 s的情況下，取得了優于Greedy算法32.7%的分配價值和穩定的工人移動距離，可以證明本文方法的有效性.

Fig. 12 Comparison of task assignment performance under different time of duration圖12 不同持續時間下任務分配性能對比

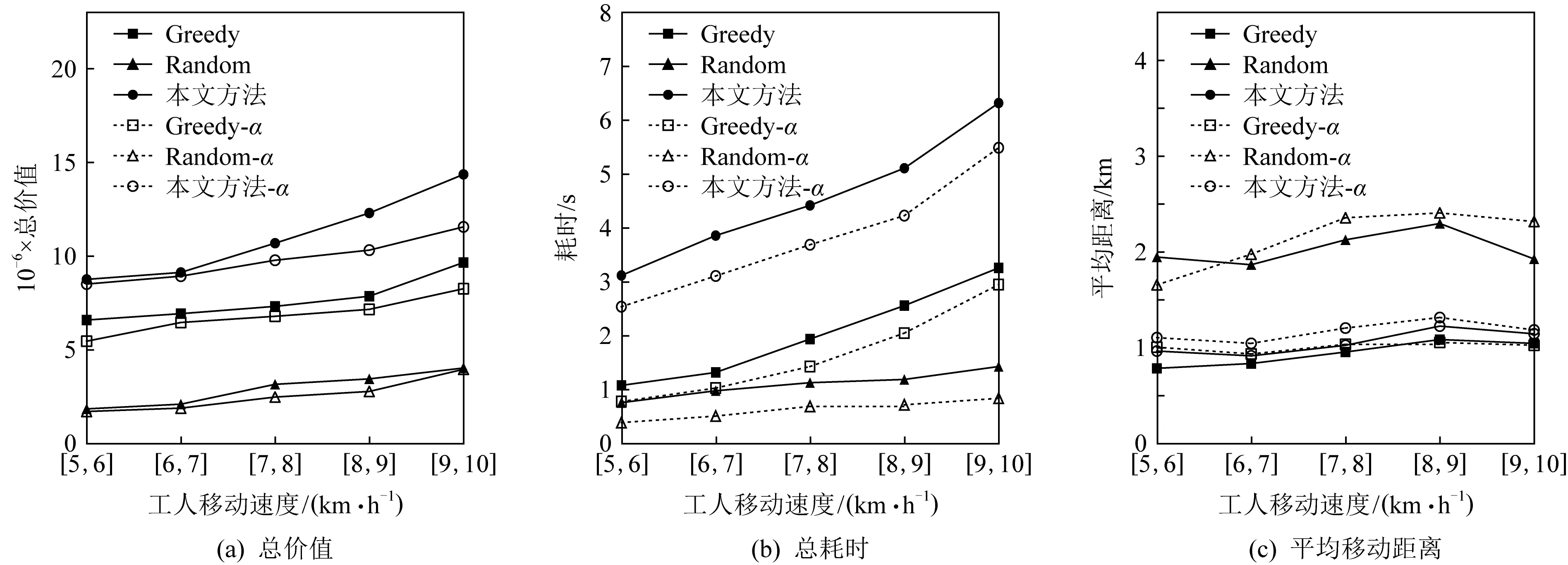
Fig. 13 Comparison of task assignment performance under different movement speed of workers圖13 不同工人移動速度下任務分配性能對比

7 結束語

本文提出一種解決空間眾包任務分配問題的方法，使用基于軌跡的任務位置預測模型和基于核密度估計的工人位置預測模型預測了未來時刻任務/工人的分布，設計了一種基于位置預測的任務分配方法來尋找盡可能好的分配.本文通過大量實驗證實了所提方法的效率和有效性，任務預測和工人預測的準確率優于其他算法，且分配方法能取得遠優于基礎算法的分配效果.本文通過大量實驗證實了所提方法的效率和有效性，任務預測和工人預測的準確率優于其他算法，且分配方法能取得遠優于基礎算法的分配效果.但在工人預測和分配工作中，沒能計算出預測工人的出現概率，只是在預測工人沒有出現的情況下盡可能早地把配對的任務重新分配，導致工人預測不精準時分配效果變差.在未來進一步研究中會針對該問題尋找更優的解決辦法，研究更復雜情景中的任務分配方法，實現空間眾包中復雜任務(多個工人分配一個任務)，及特定路線任務(根據工人移動路線分配多個任務)的分配方法.此外，將應用文獻[24-27]中位置預測算法提高眾包任務分配的準確性.

致謝

：本文實驗部分使用的數據來自滴滴出行“蓋亞”數據開放計劃(Didi Chuxing GAIA Initiative).

作者貢獻聲明

：徐天承參與研究和文章撰寫，包括算法研究、設計論文框架、起草文章和實驗等工作；喬少杰參與研究和文章撰寫，包括算法提出、設計研究方案、修訂論文和指導性支持等工作；武俊參與研究，包括采集整理數據統計分析和實施研究過程等工作；韓楠參與研究，包括采集整理數據、算法設計等工作；岳昆參與工作支持，包括理論基礎和數據支持；易玉根參與研究，包括數據采集與處理；黃發良參與工作支持，包括數據和實驗支持；元昌安參與研究，包括算法設計及修訂研究方案.