基于VMD 的TFPF 微震數據隨機噪聲去除方法應用研究
楊 勇 張忠政 程 浩
(1.鞍鋼集團礦業弓長嶺有限公司露采分公司,遼寧 遼陽 111007;2.東北大學資源與土木工程學院,遼寧 沈陽 110819)
在金屬礦山開采過程中,微震監測作為礦山安全開采的主要監測手段之一,得到了廣泛的應用[1]。通過監測井下作業、巖體破裂等因素激發的彈性波信號,利用拾取到的不同傳感器的信號進行微震源定位,進而為預警井下事故提供依據。微震數據有效信號的到時拾取是微震源定位處理過程的關鍵步驟之一,直接影響反演結果的準確性。但金屬礦山開采環境復雜,通常所采集到的微震數據中包括了大量的隨機噪聲,嚴重影響了微震數據有效信號到時拾取的精度。所以,對微震數據進行隨機噪聲去除處理是提高有效信號到時拾取精度的關鍵步驟。
時頻峰值濾波(Time-Frequency Peak Filtering,TFPF)作為一種時頻分析方法,它通過求解信號的偽維格納—維利分布(Pseudo Wigner-Ville Distribution,PWVD)頻譜來估計瞬時頻率,可以克服變換域中基函數的影響,同時又無需任何的假定條件即可達到去除噪聲的目的[2]。憑借其獨特的優越性和有效性,TFPF 已逐步地被廣泛應用于多種類數據的隨機噪聲去除。林紅波等[3-8]對TFPF 去噪方法進行了較為系統的研究,并將其應用于實際地震數據隨機噪聲去除。但由于TFPF 較為適宜處理平穩信號,所以,固定窗長制約了對于非平穩信號隨機噪聲去除的效果。
上世紀90 年代,Huang 等[9-12]針對信號非平穩問題提出了經驗模態分解(Empirical Mode Decomposition,EMD)方法。該方法是一種自適應分解方法,無需任何假定條件即可將信號分解成模態分量,突出信號的物理特性。但是這種方法會帶來模態混疊的問題。針對上述問題,變分模態分解方法(Variational Mode Decomposition,VMD)被提出,該方法通過估算各信號分量的信號主頻與帶寬,將原始信號分解成主頻不同帶寬不同的信號分量,解決了模態混疊的問題,使信號分解成頻率不同的近似平穩信號。基于VMD 分解方法的優越性,劉沖等[13]和喬云等[14]將其結合于小波變換應用于不同領域的去噪研究。
通過上述TFPF 與VMD 方法的特點分析,本研究提出了一種基于VMD 的TFPF 隨機噪聲壓制方法。首先,將含噪信號通過VMD 分解,獲取若干個不同主頻占優的近似平穩信號分量;然后,對不同頻率的信號分量靈活地選取不同的窗長進行TFPF 去噪,得到處理后的各信號分量;最后,進行信號重構,獲取隨機噪聲去除以后的信號。并將通過理論與實際微震數據進行該方法有效性的驗證。
1 變分模態分解(VMD)
VMD 是一種基于模態分解的自適應性較高的信號分解算法。VMD 通過將模態估計轉化為變分問題,解決該變分問題的構造和求解來確定非平穩信號中不同的信號主頻與帶寬,將原始信號分解成K個具有一定帶寬的信號模態分量,進而將有效信號和噪音分為不同的模態分量區分開來。VMD 分解的結果要求各模態分量的頻帶寬度之和最小,其分解出來的各階模態分量相加即可得到原始信號。
VMD 將信號看作是不同的具有一定帶寬的信號分量組成:
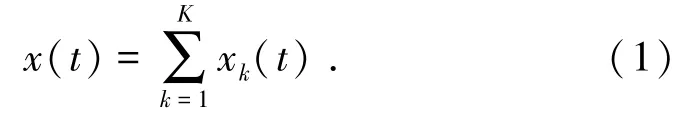
通過對信號分量進行希爾伯特變換以得到其單邊頻譜,隨后將各信號分量頻譜調整到以估計中心頻率為中心的基頻帶上,并估計各信號分量的帶寬,由此引出約束性變分問題。VMD 的約束方程式為
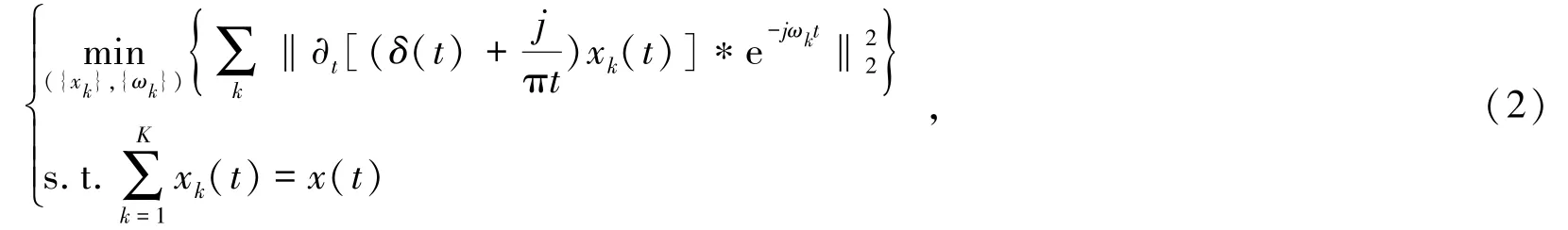
式中,{xk}為第k個分量;{ωk}為各信號分量的中心頻率;?t為Tikhonov 矩陣;δ(t)為脈沖函數;*表示卷積;x(t)是原始信號。
為了解決式(2)約束性問題,引入二次懲罰因子和Lagrange 乘法算子,將上述約束性變分問題轉化為無約束優化問題:
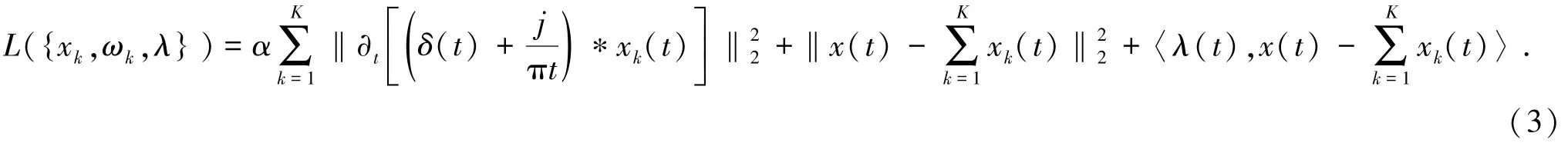
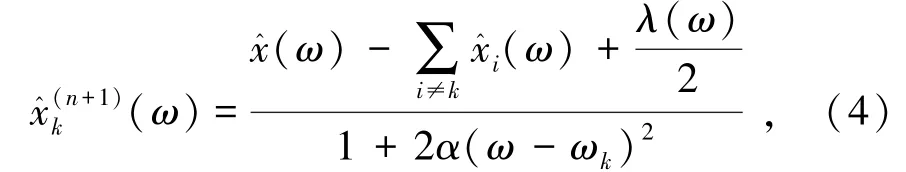
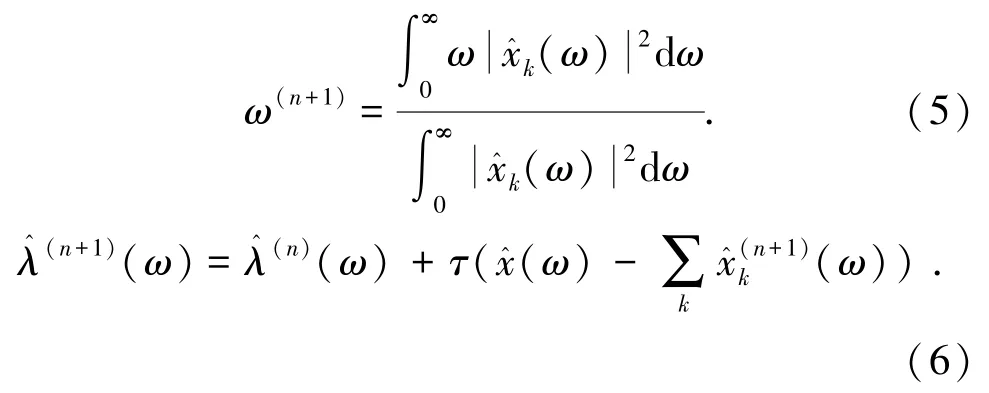
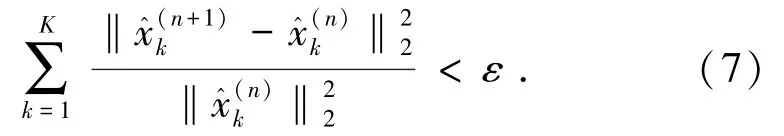
式(6)和式(7)中,τ表示的是噪聲容限參數,ε為給定的一個大于0 的判別精度。當迭代結果滿足式(7)中的收斂條件,則迭代完成,原始信號被分解為K個信號分量。
2 時頻峰值濾波(TFPF)
TFPF 算法通過頻率調制因子μ對含噪信號進行頻率調制,得到解析信號,通過求解析信號的偽維格納—維利分布(PWVD)頻譜及其峰值,得到解析信號的瞬時頻率估計,達到去噪的目的。其具體步驟如下:
(1)將含噪信號表示為有效信號和隨機噪聲的疊加:
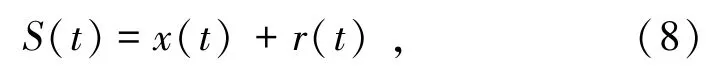
式中,x(t)為有效信號;r(t)為隨機噪聲。
(2)用一個頻率調制因子μ對包含隨機噪聲的信號進行頻率調制:

(3)求解析信號的偽維格納—維利分布頻譜(PWVD):
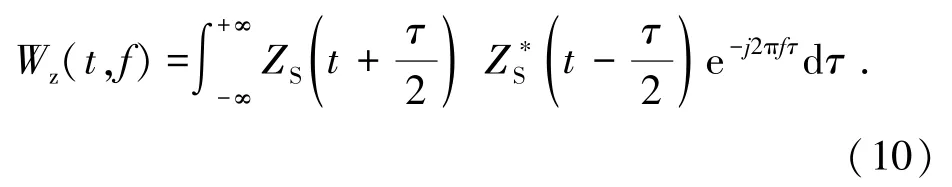
(4)求解析信號的PWVD 分布頻譜的峰值,作為解析信號瞬時頻率估計:
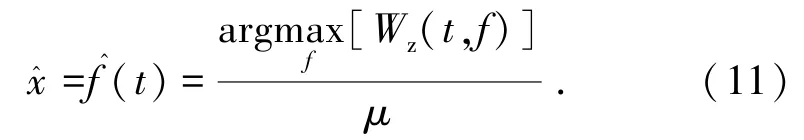
在TFPF 算法中,窗長的選擇會對信號的去噪效果產生影響。通過理論數據對TFPF 固定窗長的問題進行探討。對理論數據進行加噪處理,得到含噪信號。再分別選取窗長為7、11、15,對含噪信號進行濾波,如圖1所示。從處理結果來看,各窗長處理結果都能對噪聲進行壓制,還原出原始信號,說明TFPF算法在噪聲去除的效果上能取得良好的效果。分別選取波峰處和低振幅信號處進行局部顯示,可以觀察到在波峰處,短窗長結果有更好的信號擬合度,長窗長則存在波峰擬合度較低的問題;在低振幅信號處,長窗長對噪聲的去除效果更加明顯,而短窗長去除噪聲的效果相比長窗長較差。
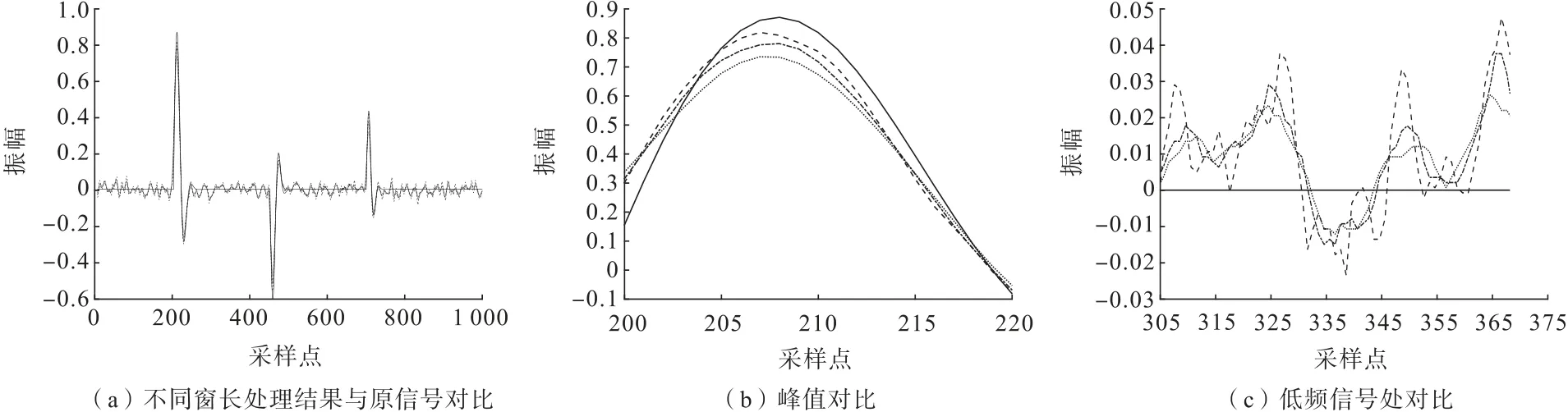
圖1 TFPF 固定窗長影響Fig.1 Effect of fixed window length of TFPF
3 基于VMD 的TFPF 隨機噪聲去除方法
根據地震數據的經驗公式,TFPF算法中固定窗長的選取:
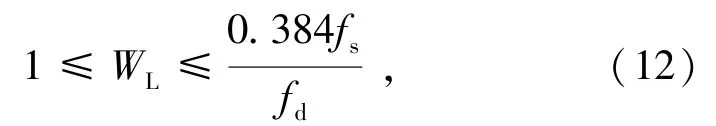
式中,fs為地震波的采樣頻率;fd為主頻。
由式(12)可知,TFPF 方法中窗長長度與微震信號的采樣頻率成正比,與微震信號的主頻成反比,若fs增大或者fd減小,則窗長相應變大,且窗長取值通常為奇數。因此在利用TFPF 處理高頻信號時,應采用短窗長進行處理,而處理低頻信號時,應采用長窗長進行處理。這樣TFPF 算法在進行信號去噪的過程中既能有效地壓制噪聲也能更好地保持有效信號的幅值。
本文方法的處理流程如下:
(1)對含噪信號進行VMD 分解,將信號分解成具有不同主頻占優的若干個近似平穩信號分量。
(2)通過上述窗長選取原則,對高頻信號分量使用短窗長進行TFPF 去噪,對低頻信號分量采用長窗長進行TFPF 去噪。
(3)將TFPF 去噪后的各階信號分量進行精確的信號重構,獲取隨機噪聲壓制以后的結果。
4 理論數據測試
選用3 個主頻分別為20,25,30 Hz,帶寬分別為2,3,4 的Ricker 子波組合作為人工合成信號進行理論數據實驗。該信號采樣率為1 ms,共計1 000 個采樣點。向該信號中加入隨機噪聲,使信號的信噪比降低至5 dB 左右,此時,合成信號被噪聲污染嚴重,低頻處有效信號基本被噪聲淹沒,原始有效信號無法被識別出來。利用VMD 分解將原始合成信號和加噪信號進行信號分解,取分解信號分量個數K=4,可以得到主頻不同帶寬不同的4 階信號分量,如圖2所示。
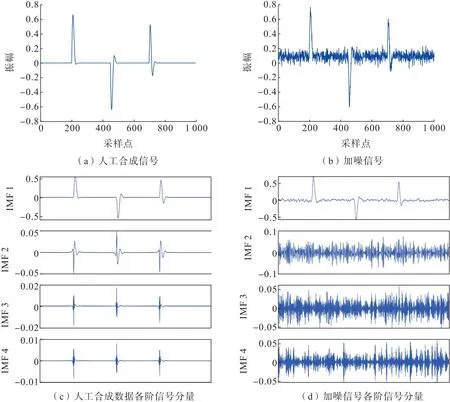
圖2 理論數據模型Fig.2 Theoretical data model
對比原始合成信號和含噪信號的VMD 分解結果,可以觀察到原始合成信號經過加噪處理后,其VMD 分解得到的4 階分量中第一信號分量出現低振幅噪聲,剩余三階信號分量基本被噪聲覆蓋,無法識別出有效信號。根據TFPF 窗長選擇規則,分別對含噪各階信號分量靈活地選取利用TFPF 去噪的自適應窗長,進行TFPF 降噪處理,再將經過TFPF 降噪后各階信號分量進行信號重構,得到壓噪后的信號。進行TFPF去噪后,各階信號分量的噪聲都有明顯的壓制(圖3)。對上述壓噪處理后各階分量進行信號重構,即可得到去噪信號(圖4)。
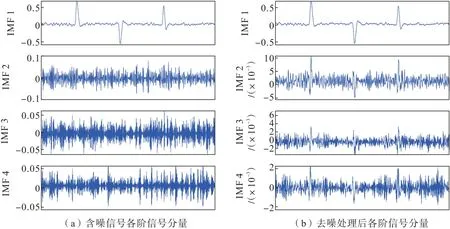
圖3 各階信號分量對比Fig.3 Comparison of signal components of different order
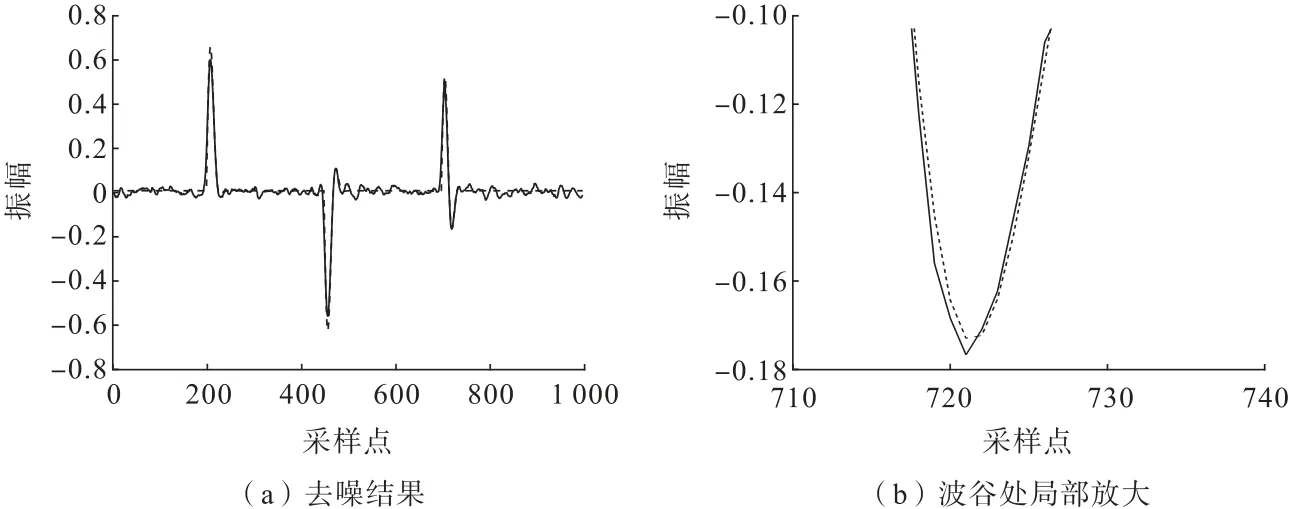
圖4 人工合成數據壓噪信號Fig.4 Denoising signal of theoretical data
本文方法是將VMD 分解與TFPF 相結合,通過分解原始信號并將各信號分量以合理的窗長進行TFPF 去噪,為了證明其有效性,下面分別應用不同固定窗長TFPF 去噪方法與本文VMD-TFPF 去噪方法對上述理論數據進行隨機噪聲的去除結果對比。為了更充分直觀地展示實驗成果,將原始數據不同固定窗長(取窗長長度為7、11、15)TFPF 去噪方法和VMD-TFPF 去噪方法的去噪結果置于同一參考系中,并將其波峰、波谷處局部放大進行保幅、保真、去噪效果的對比,如圖5所示。

圖5 人工合成數據壓噪對比Fig.5 Comparison of denoising result of theoretical data
觀察去噪結果對比圖,固定窗長TFPF 去噪和VMD-TFPF 去噪結果都可以有效地壓制隨機噪聲,將原始信號還原出來。觀察波峰數據(圖5(b)),本文方法在去噪效果和保幅保真上達到平衡,與原始數據擬合度更高,而窗長為7 的TFPF 去噪效果其有效信號遭到破壞,而窗長為11、15 的TFPF 去噪效果其幅值有一定的衰減。觀察波谷數據(圖5(c)),亦可見,本文的去噪結果與原始信號擬合度更高。
為了進一步說明本文方法的有效性,表1 給出了含噪信號與去噪所得信號均方誤差(MSE)、信噪比(SNR)和峰值信噪比(PSNR)的對比。
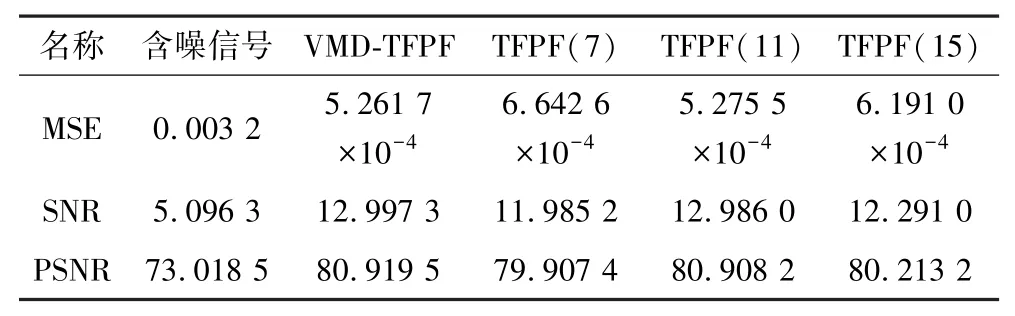
表1 合成數據實驗的MSE、SNR和PSNR 對比Table 1 Comparison of MSE,SNR and PSNR for the synthetic-data experiment
理論數據實驗結果表明,本文方法的MSE 值比固定窗長TFPF 去噪方法更低,與原始信號擬合度更高;而在信噪比和峰值信噪比的指標上,VMD-TFPF去噪方法和固定窗長TFPF 去噪方法都有顯著的提高,說明結果能夠壓制噪聲,達到還原出原始信號的目的,但本文方法的SNR和PSNR 比固定窗長TFPF去噪方法更高,其去噪效果最佳。
5 實際數據測試
選取某地實際礦山微震數據(圖6)進行實際數據VMD-TFPF 方法的應用測試,觀察可見,實際信號中包含有大量的隨機噪聲,這對有效信號的識別產生了極大的干擾。對該微震數據進行傅里葉變換,結果如圖7所示。經過傅里葉變換后,分析其頻率特征發現,該信號頻率主頻基本介于0 ~50 Hz 之間。由該地區微震數據的頻譜特征可知,數據的有效信號部分具有低頻特性,而在實際數據的傅里葉變換圖中可見,該信號在高頻部分也有分布,說明該部分是由隨機噪聲引起的,因而應該壓制引起高頻分布的隨機噪聲。
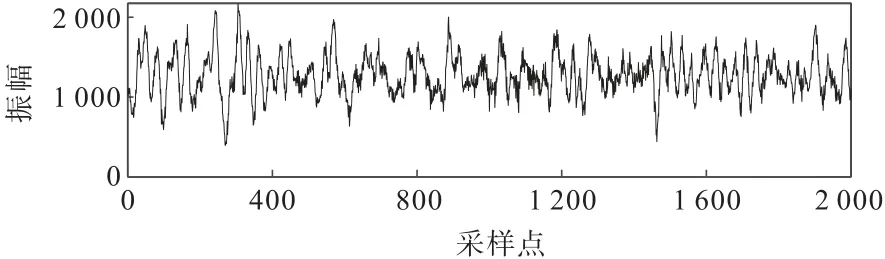
圖6 某地實際礦山微震信號Fig.6 Actual micro-seismic data
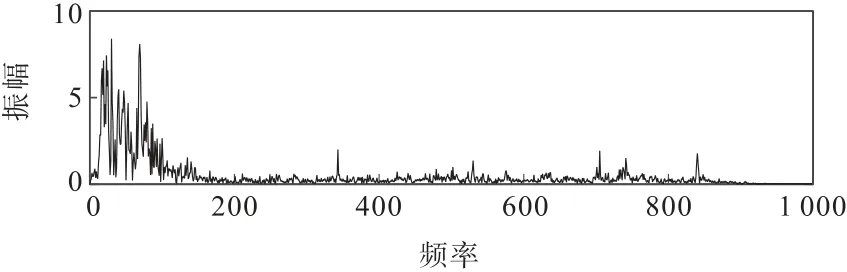
圖7 實際礦山微震信號頻譜圖Fig.7 Frequency spectrum of the actual micro-seismic data
如圖8所示,對該實際數據進行VMD 分解,取K值為8,由式(12)TFPF 算法窗長選取原則,對8 個分量分別選取自適應窗長進行TFPF 去噪處理。最后將各個處理后的信號分量組進行信號重構操作,以還原出有效信號。觀察利用VMD-TFPF 方法壓噪處理的結果,并與實際數據進行對比(圖9),顯示本文方法能夠很好地去除隨機噪聲,而且還保護了信號的幅值,較為真實地還原出了有效信號。
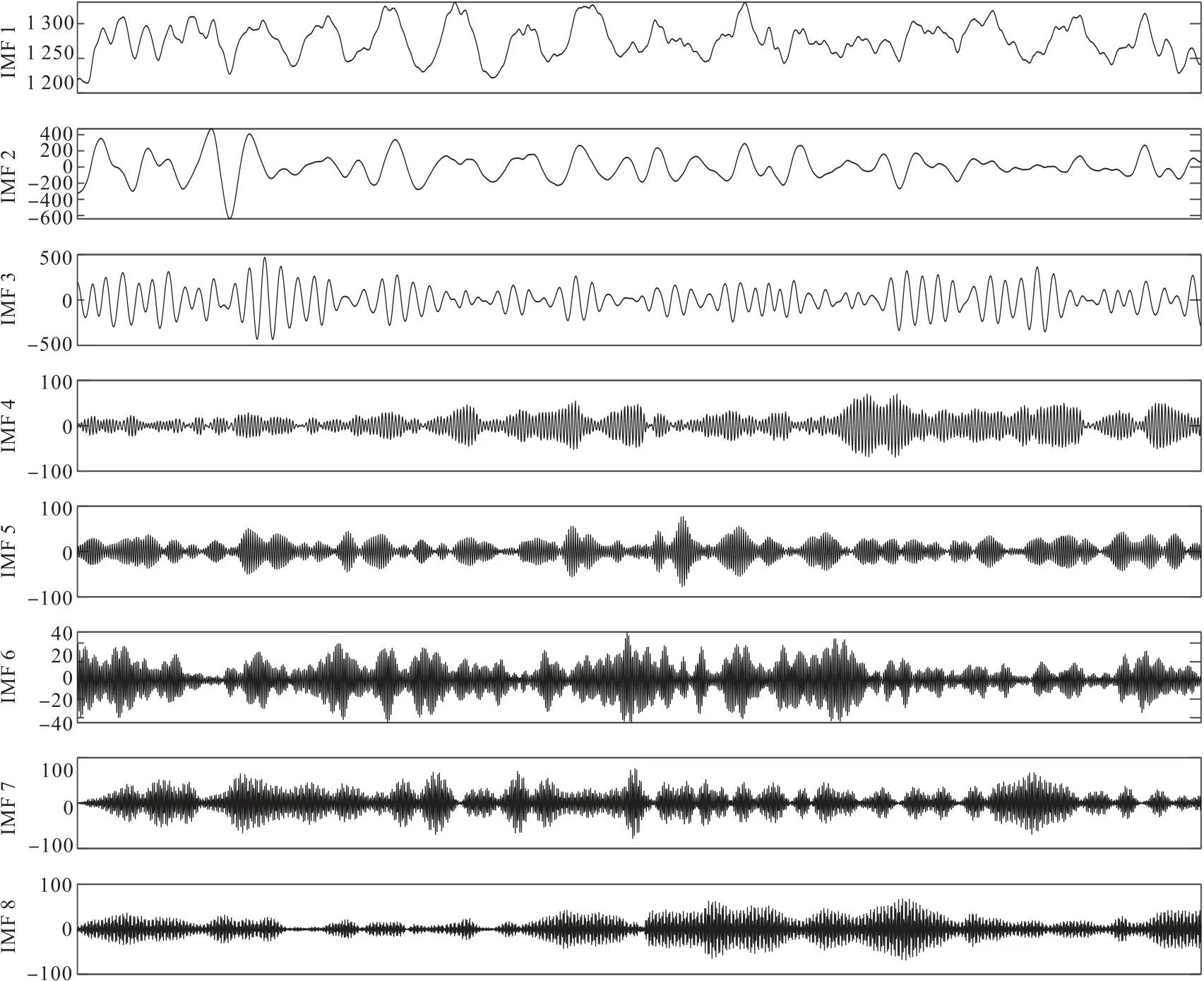
圖8 實際礦山微震信號VMD 分解各階分量圖Fig.8 VMD decomposition of actual mine microseismic signals
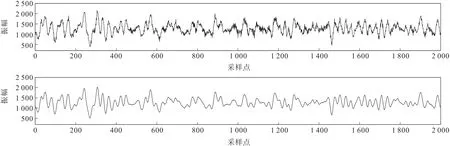
圖9 實際去噪結果對比Fig.9 Comparison of actual denoising effects
6 結 論
微震數據中隨機噪聲的有效去除,對于準確識別微震事件的到達時間,進而提高微震源定位的精度具有重要的實際意義。針對金屬礦山微震數據中隨機噪聲的去除問題進行研究,提出了一種基于VMD 的TFPF 隨機噪聲去除方法,充分結合2 種方法的優勢,通過理論數據和實際數據的測試,可得以下結論:
(1)微震數據通過VMD 方法進行分解,可獲得近似平穩的多個信號分量,避免了直接利用TFPF 方法進行非平穩信號的處理。
(2)TFPF 方法可針對不同近似平穩的多個信號分量選取對應的窗長,進而達到最大限度地去除隨機噪聲、保留有效信號。
(3)基于VMD 的TFPF 去噪方法能夠有效地去除隨機噪聲,提高微震數據的信噪比,同時,更好地保留有效信號的幅值。

