TC4鈦合金疲勞壽命不確定度評定

李 凱, 盧 奇, 鄭 程, 巴發海

(上海材料研究所 上海市工程材料應用與評價重點實驗室, 上海 200437)

在實際測量過程中，測量值是包含測量過程中的隨機效應以及系統效應引入不確定度真值的估計值。不確定度表征了測量結果的可靠程度，是量值溯源體系中不可缺少的一部分。JJF 1059.1—2012 《測量不確定度評定與表示》與ISO/IEC GUIDE 98-3:2008 《測量的不確定性 第3部分：測量不確定性的表達指南》中的內容是不確定度評定最常用和最基本的方法，也稱為GUM法。GUM法評定不確定度的主要步驟包括：不確定度來源分析、測量模型建立、標準不確定度計算、合成不確定度計算、擴展不確定度計算以及結果表示等[1]。

在計量校準領域，依據GUM法評定不確定度已經得到廣泛應用，CNAS-CL01：2018 《檢測和校準實驗室能力認可準則》第7.8.4.1條款中規定校準報告必須包含校準結果的不確定度。隨著行業的發展，檢測領域也越來越重視不確定度的評定，GB/T 228.1—2021 《金屬材料 拉伸試驗 第1部分：室溫試驗方法》對拉伸試驗中抗拉強度、斷后伸長率等性能的不確定度評定進行了詳細介紹。對于疲勞試驗，僅有GB/T 24176—2009 《金屬材料 疲勞試驗 數據統計方案與分析方法》給出了升降法測量疲勞強度結果標準偏差的計算方法。疲勞壽命不確定度評定也引起了行業專家的重視，并取得了一些研究成果。冉學臣[2]在假設對數疲勞壽命服從正態分布的前提下，得出45鋼旋轉彎曲疲勞對數壽命擴展不確定度為0.19～0.20。高怡斐等[3]對GB/T 24176—2009中的數據進行了深入分析和計算，得出對數疲勞壽命擴展不確定度為0.09～0.11。總體來說,由于影響疲勞壽命的因素多且復雜，因此尚未形成疲勞壽命不確定度的統一評定方法。筆者以TC4鈦合金為例，給出了一種通用的疲勞壽命不確定度的評定模型與實例，數據正態性檢驗、異常值判定等關鍵步驟使得不確定度評定過程更為嚴謹與完善。

1 試驗方法

試驗材料為TC4鈦合金棒材。采用光電直讀光譜儀進行化學成分分析，根據GB/T 228.1—2021，用電子萬能試驗機進行拉伸試驗，試樣數量為3支，拉伸速率為1 mm/min。根據GB/T 3075—2021 《金屬材料 疲勞試驗 軸向力控制方法》，采用高頻疲勞試驗機進行疲勞試驗，試樣數量為10支，軸向加載，波形為正弦波，應力比為0.1，最大應力為700 MPa，試驗頻率由試驗系統的共振頻率確定。拉伸試驗與疲勞試驗的試樣結構如圖1所示。

圖1 拉伸試驗與疲勞試驗的試樣結構示意

2 試驗結果

TC4鈦合金的化學成分分析結果如表1所示，結果符合GB/T 2965—2007 《鈦及鈦合金棒材》對TC4鈦合金棒材成分的規定。TC4鈦合金試樣抗拉強度測試結果如表2所示，試樣抗拉強度的平均值為1 079 MPa，試樣的疲勞壽命測試結果如表3所示。

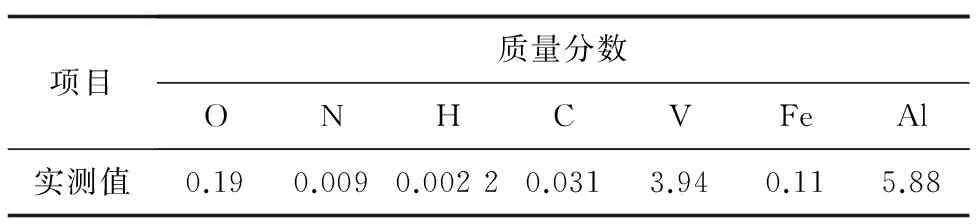
表1 TC4鈦合金的化學成分分析結果 %

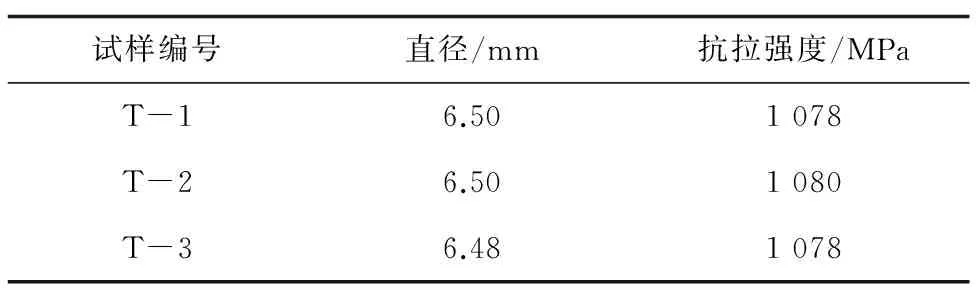
表2 TC4鈦合金試樣的抗拉強度測試結果

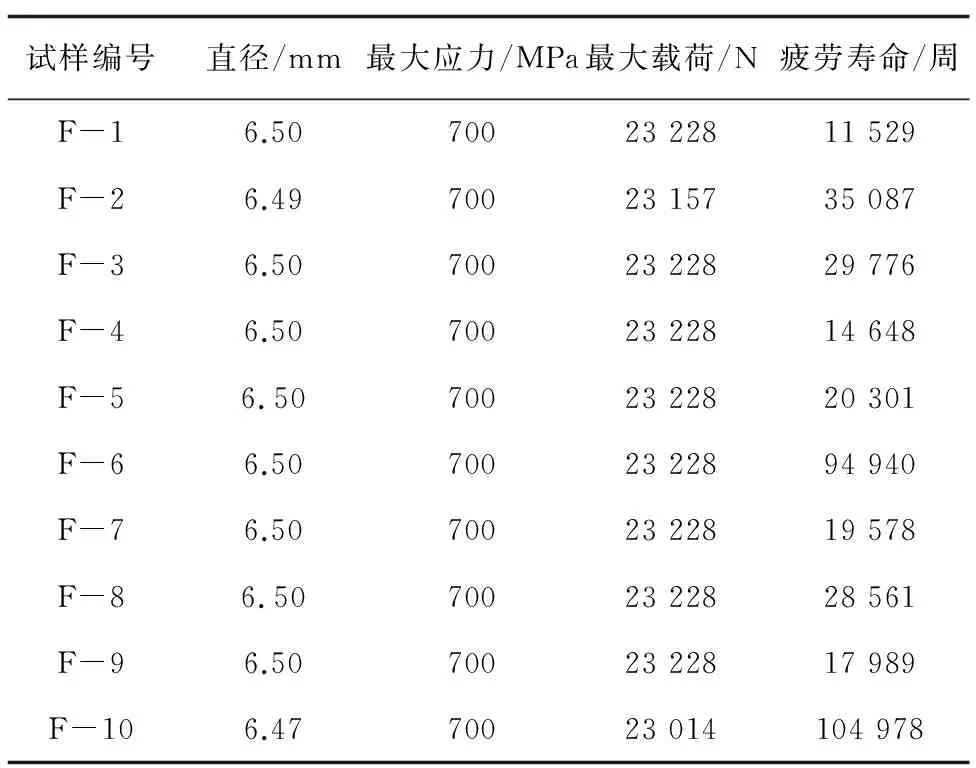
表3 TC4鈦合金試樣的疲勞壽命測試結果

2.1 正態性檢驗

通常指定應力下的疲勞壽命或對數疲勞壽命服從正態分布，不確定度評定以及奇異值判定都需要明確其分布規律，參照GB/T 4882—2001 《數據的統計處理和解釋 正態性檢驗》進行正態性檢驗。Shapiro-Wilk檢驗適用于樣本數量8≤n≤50的正態檢驗。Shapiro-Wilk檢驗為一個完全樣本方差分析形式的檢驗。檢驗統計量為樣本次序統計量線性組合的平方。Shapiro-Wilk檢驗步驟如下所述。

零假設：樣本的總體數據服從正態分布。

將n個獨立觀測值按非降序記為x1,x2,x3,…，xn，然后計算Shapiro-Wilk檢驗的輔助量S，如式(1)所示。

S=∑ak[xn+1-k-xk]

(1)

式中:當n為奇數時，下標k為1,2,…,(n-1)/2；當n為偶數時，下標k為1,2,…,n/2;ak為與樣本量n相關的特定值，可以查表得到。

檢驗統計量W的計算方法如式(2)所示。

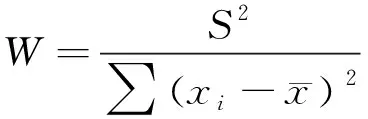
(2)

在顯著性水平α=p下，如果W小于其p分位數(p=α)，則拒絕零假設。TC4鈦合金疲勞壽命Shapiro-Wilk檢驗計算結果如表4所示。

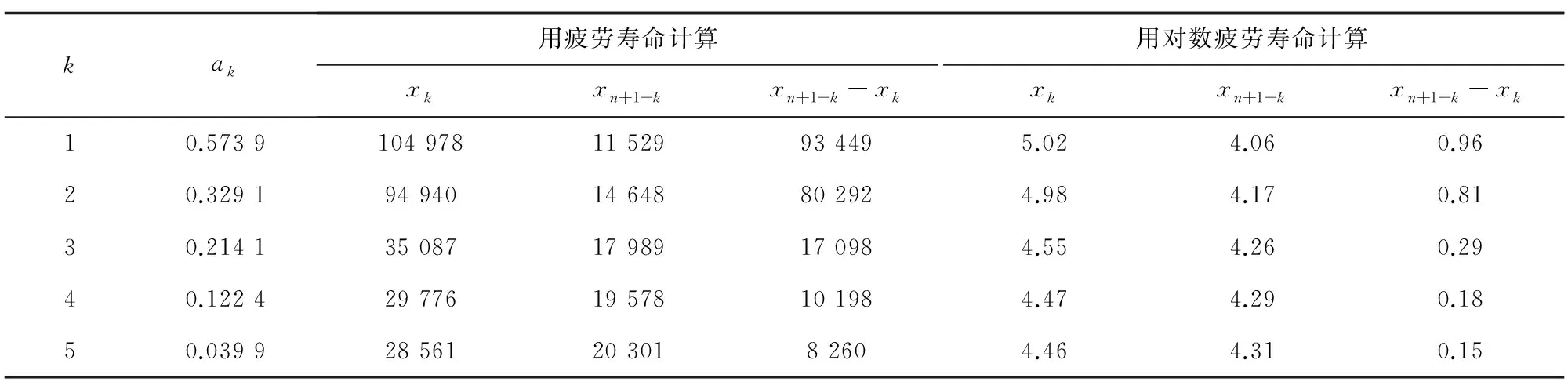
表4 TC4鈦合金疲勞壽命Shapiro-Wilk檢驗計算結果

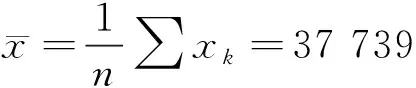
(3)

S=∑ak(xn+1-k-xk)=85 293

(4)

則計算得：W為0.714。

當n=10，且p=α=0.05時,p分位數為0.842，由于計算得到的W小于該值，因此在顯著性水平α=0.05上拒絕零假設，即根據Shapiro-Wilk檢驗，疲勞壽命不服從正態分布。按同樣方法對對數疲勞壽命進行Shapiro-Wilk檢驗。

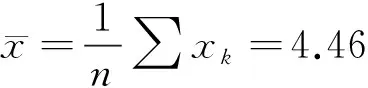
(5)

S=∑ak(xn+1-k-xk)=0.908

(6)

W>W(n=10,α=0.05)

(7)

根據Shapiro-Wilk檢驗，對數疲勞壽命服從正態分布。

2.2 異常值判定

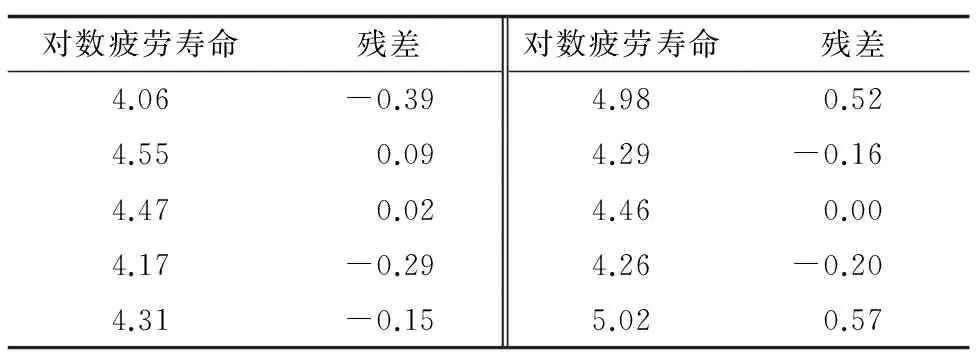
表5 TC4鈦合金對數疲勞壽命異常值判定

表5中絕對值最大的殘差v=0.57，相應的對數疲勞壽命5.02為可疑值，則

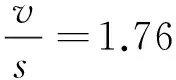
(8)

按照p=0.95，α=0.05，n=6時，格拉布斯臨界值G(0.05,10)=2.176，則

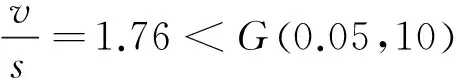
(9)

3 不確定度評定

3.1 不確定度來源分析

疲勞試驗屬于破壞性試驗，疲勞壽命不確定度評定不描述由材料不均勻性引起的分散，不確定度來源于從理想均質材料中提取的不同試驗、不同試驗機、不同實驗室獲得的數據分散性。從儀器、環境、人員、方法等方面考慮，不確定度來源主要有測量重復性引入的不確定度分量u1、試驗機力值引入的不確定度分量u2、試樣尺寸測量引入的不確定度分量u3等3部分。

3.2 數學模型

試驗機循環次數N為輸入量，對數疲勞壽命lgNf為輸出量。因此建立數學模型如式(10)所示。

lgNf=lgN

(10)

式中：Nf為疲勞壽命；N為試驗機循環次數。

式(3)中沒有直接體現出試驗機力值、試樣直徑測量等不確定度來源分量。對于實際進行試驗后的疲勞試樣，其疲勞壽命直接通過試驗機記錄循環次數得到，這個計數本身是準確的，無需評定不確定度。疲勞壽命的定義是：在指定的應力水平下，試樣失效之前經歷的循環次數。因此疲勞強度不確定度評定過程中的輸入量是應力水平、試樣尺寸等參數，輸出量是疲勞壽命。對數疲勞壽命與應力水平可以按照線性模型分析。

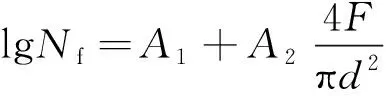
(11)

式中：F為試驗力；d為試樣直徑;A1,A2均為待定系數。

對于不同的材料、試樣形狀、加載水平，式(11)中的待定系數A1,A2均不同。當疲勞試驗中最大應力水平為材料抗拉強度時，對數疲勞壽命lgNf=0。即疲勞試驗中最大應力為抗拉強度1 079 MPa時，對應的TC4鈦合金的對數疲勞壽命lgNf=0。通過表 3中的試驗數據可知，最大應力為700 MPa時，對數疲勞壽命平均值為4.46，則將(1 079,0)，(700,4.46)分別代入式(11)可得

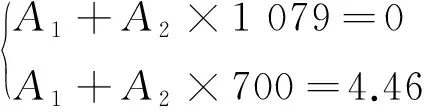
(12)

解方程組可得

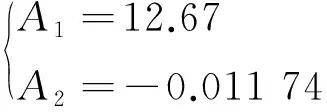
(13)

最終數學模型為

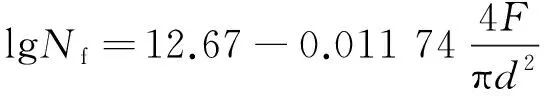
(14)

也可以通過多應力水平下疲勞壽命對待定系數進行求解。

3.3 靈敏系數

靈敏系數c1,c2,c3為模型中各個不確定度分量的偏導數,具體為

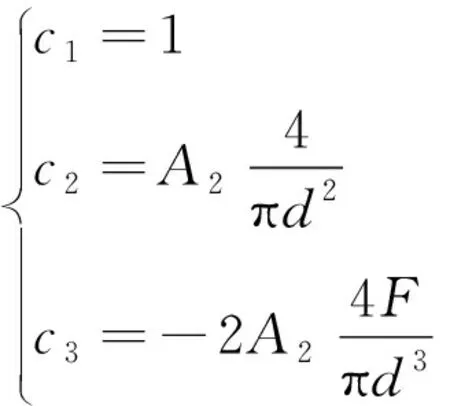
(15)

試樣直徑d=6.5 mm，試驗應力為700 MPa，試驗力F=23 228 N，代入式(15)可得

(16)

3.4 不確定度分量

3.4.1 測量重復性引入的不確定度分量u1

測量重復性引入不確定度分量按照A類標準不確定度進行評定。10次測量的標準偏差按照貝塞爾式計算。

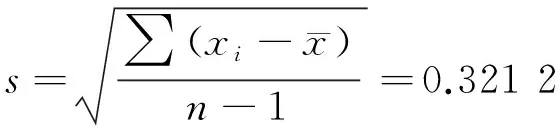
(17)

通常在指定應力水平下測試疲勞壽命時，會進行3次測量，因此測量重復性引入的不確定度分量u1=0.185 4。

A類評定的標準不確定度的自由度ν1=9。

3.4.2 試驗機力值引入的不確定度分量

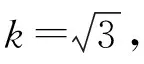
B類評定的標準不確定度的自由度為

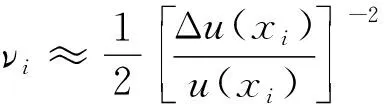
(18)

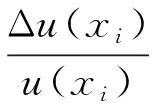
3.4.3 試樣尺寸測量引入不確定度分量

試樣尺寸測量應精確到0.5%，試樣工作段直徑為6.5 mm，最大允許誤差為±0.032 5 mm，按照B類不確定度評定，半寬區間a=0.032 5 mm，按正態分布，k=2，則試樣尺寸測量引入不確定度分量u3=0.016 25 mm。

由試驗機力值引入的不確定度分量的自由度可得，試樣尺寸測量引入不確定度分量的自由度ν3=8。

3.5 合成標準不確定度uc

測量重復性引入的不確定度分量u1、試驗機力值引入的不確定度分量u2、試樣尺寸測量引入的不確定度分量u3互不相關，由不確定度傳播率可得合成標準不確定度為

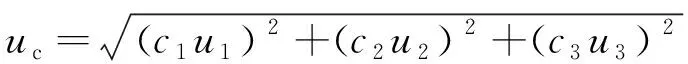
(19)

式中：u1,u2,u3為各分量標準不確定度。

各不確定度分量如表6所示。

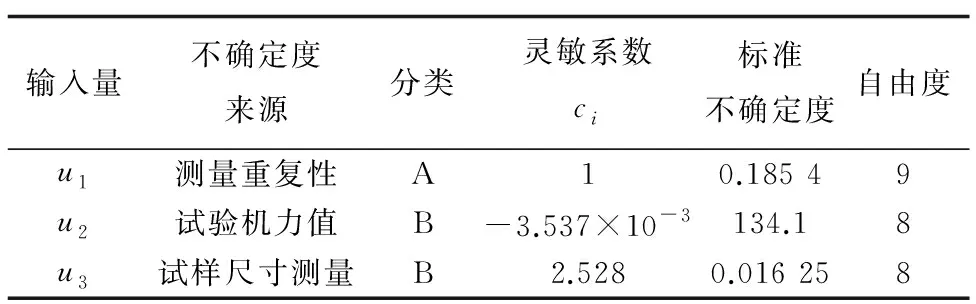
表6 各不確定度分量匯總

將表6中的數據代入式(22)可得標準不確定度uc=0.20。

當各分量間相互獨立，且輸出量接近正態分布或t分布時，合成標準不確定度的有效自由度為

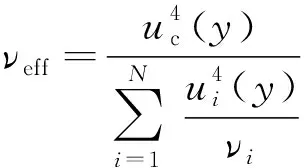
(20)

將表6中數據代入式(23)，可得νeff=11。

3.6 擴展標準不確定度

對數疲勞壽命服從正態分布，取包含因子k=2，擴展標準不確定度U=0.40。

對數疲勞壽命的擴展不確定度U=0.40。

4 結論

(1) TC4鈦合金在應力比R=0.1,最大應力為700 MPa，正弦波、軸向加載試驗條件下的疲勞壽命lgNf=4.46,U=0.40，有效自由度νeff=11。

(2) 疲勞壽命測量不確定度的來源主要有：測量重復性、試驗機力值以及試樣尺寸測量。

(3) 疲勞壽命不確定度評定模型中，疲勞壽命與應力之間的關系可以采用線性模型。

(4) 評定不確定度之前，需要進行異常值判定以及正態分布驗證。