高一上學年期末復習與總結

2022-02-13 10:42:30張文偉

中學生數理化·高一版 2022年1期

■張文偉

必修(第一冊)的主要內容是集合與常用邏輯用語,一元二次函數,方程和不等式,函數的概念與性質,指數函數與對數函數以及三角函數。同學們要理解它們的概念、性質及應用,掌握一些經典題型的解題思想與方法,注意歸納總結,逐步提高解題能力和創新思維能力。

題型1:集合的概念與運算

集合的運算主要包括交集、并集和補集運算,這也是高考對集合部分的主要考查點。對于較抽象的集合問題,需借助Venn 圖或數軸等進行數形分析,使問題直觀化、形象化,進而能使問題簡捷、準確地獲解。

例1(1)(多選題)已知集合A={2,3},B={x|mx-6=0},若B?A,則實數m等于( )。

A.0 B.1

C.2 D.3

(2)已知全集U={x|x＞0},集合A={x|3≤x＜7},B={x|2＜x＜10},C={x|5-a＜x＜a}。

①求A∪B,(?UA)∩B。②若C?(A∪B),求a的取值范圍。

解:(1)當m=0時,B=?,則B?A,符合題意。當m≠0時,,由B?A知,即m=3 或m=2。綜上可知,m=0或m=2或m=3。應選A,C,D。

(2)①A∪B={x|3≤x＜7}∪{x|2＜x＜10}={x|2＜x＜10}。

?UA={x|0＜x＜3或x≥7},(?UA)∩B={x|2＜x＜3或7≤x＜10}。

②若C=?,則5-a≥a,解得;若C≠?,則2≤5-a＜a≤10,解得。綜上可得,a≤3,即a∈(-∞,3]。

題型2:充分條件與必要條件

若p?q,且q?/p,則p是q的充分不必要條件,同時q是p的必要不充分條件;若p?q,則p是q的充要條件,同時q是p的充要條件。充分、必要條件的判斷和證明是高考的一個常考點,常與不等式等知識結合命題。學會用集合的觀點,分析和解決充分、必要條件的判斷和求參數范圍問題,提升轉化與化歸能力。

例2(1)(多選題)對于任意實數a,b,c,下列結論正確的是( )。

A.“a=b”是“ac=bc”的充分條件

B.“a+是無理數”是“a是無理數”的必要條件

C.“a=b”是“a2=b2”的充分條件

D.“a＞b”是“a＞|b|”的必要條件

(2)設p:實數x滿足A={x|x≤3a或x≥a(a＜0)},q:實數x滿足B={x|-4≤x＜-2},且q是p的充分不必要條件,求實數a的取值范圍。

解:(1)由a=b,可得ac=bc,A 正確。a+是無理數與a是不是無理數沒有關系,B錯誤。由a=b,可得a2=b2,C正確。由a＞|b|,可得a＞b,D正確。應選A,C,D。

(2)由q是p的充分不必要條件,可得BA,所以由此解得或a≤-4。故實數a的取值范圍為。

題型3:全稱量詞命題和存在量詞命題

全稱量詞強調的是“任意”“一切”“每一個”等,常用符號“?”表示,而存在量詞強調的是部分,常用符號“?”表示。對于全稱量詞命題和存在量詞命題的否定要把握兩點:一是改量詞,二是否結論。

例3(1)命題p:“?x∈R,x2＞0”,則( )。

A.p是假命題;﹁p:?x∈R,x2＜0

B.p是假命題;﹁p:?x∈R,x2≤0

C.p是真命題;﹁p:?x∈R,x2＜0

D.p是真命題;﹁p:?x∈R,x2≤0

(2)已知命題p:?x∈{x|1≤x≤4},x-a≥0,命題q:?x∈R,x2+2x+2-a=0。若命題﹁p是真命題,且命題q是真命題,求實數a的取值范圍。

解:(1)因為02＞0不成立,所以“?x∈R,x2＞0”為假命題。根據全稱量詞命題的否定是存在量詞命題可知,“?x∈R,x2＞0”的否定是“?x∈R,x2≤0”。應選B。

(2)若p:?x∈{x|1≤x≤4},x-a≥0為真命題,則a小于或等于x的最小值,即a≤1。當命題﹁p是真命題時,命題p為假命題,所以a＞1。若q:?x∈R,x2+2x+2-a=0為真命題,即方程x2+2x+2-a=0有解,則Δ=4-4(2-a)≥0,解得a≥1。當命題﹁p是真命題,且命題q是真命題時,需滿足解得a＞1,即實數a的取值范圍是(1,+∞)。

題型4:基本不等式及其應用

例4(1)已知x＞0,y＞0,2x+3y=6,則xy的最大值為____。

(2)設x＜-1,求的最大值。

題型5:不等式的性質及應用

不等式的性質的命題形式有比較大小、命題真假的判斷、不等式的證明等,解答這類問題要注意直接法和特值法的應用。

例5(1)若A=a2+3ab,B=4ab-b2,則A,B的大小關系是( )。

A.A≤BB.A≥B

C.A＜B或A＞BD.A＞B

(2)如果a,b,c滿足c＜b＜a且ac＜0,則下列選項中不一定成立的是( )。

A.ab＞acB.c(b-a)＞0

C.cb2＜ab2D.ac(a-c)＜0

解:(1)由A-B=a2+3ab-4ab+b2=a2-ab+b2=≥0,可得A≥B。應選B。

(2)由c＜b＜a,ac＜0,可得a＞0,c＜0。對于A,由b＞c,a＞0,可得ab＞ac,A 正確。對于B,由b＜a,c＜0,可得c(b-a)＞0,B正確。對于C,由c＜a,b2≥0,可得cb2≤ab2,但不一定得到cb2＜ab2,即C 不一定成立。對于D,由ac＜0,a-c＞0,可得ac(ac)＜0,D 正確。應選C。

題型6:一元二次不等式的解法

一元二次不等式的解法充分體現了三個“二次”之間的內在聯系,解此相關問題應把握三個關鍵點:圖像的開口方向;是否有根;根的大小關系。對于一元二次不等式的恒成立問題,利用數形結合法可幫助求解。

例6(1)若不等式ax2+3x+2＞0 的解集為{x|b＜x＜1},求a,b的值。

(2)求關于x的不等式ax2+3x+2＞-ax-1(其中a＞0)的解集。

解:(1)將x=1代入ax2+3x+2=0,可得a=-5。

由a=-5得不等式ax2+3x+2＞0即5x2-3x-2＜0,解得不等式的解集為。據此可得。

(2)不等式ax2+3x+2＞-ax-1可化為ax2+(a+3)x+3＞0,即(ax+3)(x+1)＞0。當,即0＜a＜3時,原不等式的解集為;當,即a=3 時,原不等式的解集為{x|x≠-1};當,即a＞3時,原不等式的解集為。

綜上所述,當0＜a＜3時,原不等式的解集為;當a=3時,原不等式的解集為{x|x≠-1};當a＞3時,原不等式的解集為。

題型7:不等式在實際問題中的應用

不等式的應用問題常以函數為背景,多是解決現實生活、生產中的優化問題,在解題中主要涉及不等式的解法、基本不等式求最值等。根據題設條件構建數學模型是解答這類問題的關鍵。

例7某房地產開發公司計劃在一樓區內建造一個長方形公園ABCD,公園由長方形A1B1C1D1的休閑區和環公園人行道(陰影部分)組成。已知休閑區A1B1C1D1的面積為4000 m2,人行道的寬分別為4 m 和10m(如圖1)。

圖1

(2)要使公園所占面積最小,則休閑區A1B1C1D1的長和寬該如何設計?

解:(1)設休閑區的寬B1C1為am,則長A1B1為axm。

由a2x=4000,可得。

故S=(a+8)(ax+20)=a2x+(8x+20)a+160=4000+(8x+20)×+4160(x＞1)。

題型8:求函數的定義域

求函數定義域的常用依據是分母不為0,偶次根式中的被開方數大于或等于0。由幾個式子構成的函數,其定義域是使各式子有意義的集合的交集。

例8(1)求函數的定義域。

(2)將長為a的鐵絲折成矩形,求矩形面積y關于一邊長x的解析式,并寫出此函數的定義域。

解:(1)要使函數有意義得解得所以函數的定義域是{x|1≤x≤5且x≠3}。

(2)設矩形的一邊長為x,則另一邊長為,所以面積。由題意可知此函數的定義域為。

題型9:求函數的解析式

求函數解析式的題型與相應的解法:(1)已知形如f[g(x)]的解析式求f(x)的解析式,使用換元法或配湊法;(2)已知函數的類型(往往是一次函數或二次函數),使用待定系數法;(3)含f(x)與f(-x)或f(x)與,使用解方程組法;(4)已知一個區間的解析式,求其對稱區間的解析式,可用奇偶性轉移法。

例9(1)函數f(x)在R 上為奇函數,當x＞0時,f(x)=,則函數f(x)的解析式為____。

解:(1)當x＜0時,-x＞0,則f(-x)=。由f(x)是奇函數,可得f(-x)=-f(x),所以-f(x)=,即當x＜0時,f(x)=。又f(x)是奇函數,所以f(0)=0。

故函數f(x)=

題型10:函數的性質及應用

函數的性質主要有定義域、值域、周期性、對稱性、單調性和奇偶性,其中單調性和奇偶性是學習的重點,利用函數的單調性和奇偶性求值、比較大小、解不等式是高考考查的主要內容。在解不等式時,要注意數形結合法的應用。

例10已知f(x)是定義在[-1,1]上的奇函數,且f(1)=1,當a,b∈[-1,1],a+b≠0時,有成立。

(1)判斷f(x)在[-1,1]上的單調性,并證明。

(2)解不等式f(x2)＜f(2x)。

(3)若f(x)≤m2-2am+1 對所有的a∈[-1,1]恒成立,求實數m的取值范圍。

解:(1)f(x)是[-1,1]上的增函數。

任取x1,x2∈[-1,1],且x1＜x2,則f(x1)-f(x2)=f(x1)+f(-x2)。由,可得＞0。因為x1-x2＜0,所以f(x1)-f(x2)＜0,所以f(x)是[-1,1]上的增函數。

(2)由(1)得f(x)在[-1,1]上單調遞增,所以不等式f(x2)＜f(2x)等價于解得0＜x≤。

(3)要使f(x)≤m2-2am+1對所有的x∈[-1,1],a∈[-1,1]恒成立,只需f(x)max≤m2-2am+1對所有的x∈[-1,1],a∈[-1,1]恒成立。

因為f(x)max=f(1)=1,所以1≤m2-2am+1 對任意的a∈[-1,1]恒成立,即m2-2am≥0對任意的a∈[-1,1]恒成立。令函數g(a)=-2ma+m2,只需滿足解得m≤-2或m≥2或m=0。故實數m的取值范圍是(-∞,-2]∪{0}∪[2,+∞)。

題型11:指數函數、對數函數的圖像及應用

函數y=ax與y=logax(a＞0,且a≠1)的圖像關于直線y=x對稱,前者恒過(0,1)點,后者恒過(1,0)點,兩函數的單調性均由底數a決定。在解題中要注意由翻折、平移等變換得出的函數圖像。

例11(1)已知a＞0,且a≠1,則函數f(x)=ax和函數的圖像可能是( )。

A.[-1,0) B.[0,+∞)

C.[-1,+∞) D.[1,+∞)

解:(1)由題意知函數f(x)=ax與的單調性相同,排除D。由g(-1)=loga1=0,可排除A,B。應選C。

(2)函數g(x)=f(x)+x+a存在2個零點,即關于x的方程f(x)=-x-a有2個不同的實根,也即函數f(x)的圖像與直線y=-x-a有2個交點。作出直線y=-x-a與函數f(x)的圖像,如圖2所示。

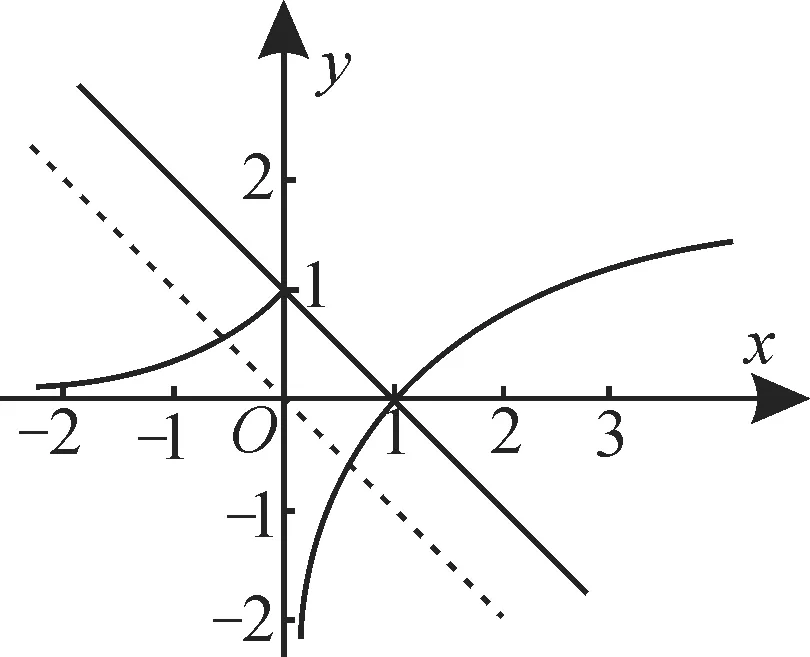
圖2

由圖可知,要使g(x)存在2 個零點,需滿足-a≤1,解得a≥-1。應選C。

題型12:指數函數、對數函數的性質及應用

指數函數、對數函數的性質命題角度有:數值的比較大小、方程或不等式的求解問題。要注意解含有對數式的方程或不等式時,不能忘記對數的真數大于0,以免出現增解或漏解。

例12(1)若0＜x＜y＜1,則( )。

A.3y＜3xB.logx3＜logy3

Cl.og4x＜log4yD.

(2)已知a＞0,a≠1,且loga3＞loga2,若函數f(x)=logax在區間[a,3a]上的最大值與最小值之差為1。

①求a的值。②若1≤x≤3,求函數y=的值域。

解:(1)函數y=3x在R 上單調遞增,由0＜x＜y＜1,可得3x＜3y,A 錯誤。當0＜a＜1時,函數y=logax在x∈(0,1)上“底小圖高”,由0＜x＜y＜1,可得logx3＞logy3,B錯誤。函數y=log4x在(0,+∞)上單調遞增,則log4x＜log4y,C正確。函數在R 上單調遞減,則,D 錯誤。應選C。

(2)①由loga3＞loga2,可知f(x)=logax在[a,3a]上為增函數,所以loga(3a)-logaa=1,即loga3=1,可得a=3。

題型13:函數的零點與方程的根

函數的零點就是相應方程的根,也是相應函數圖像與x軸交點的橫坐標。判斷函數的零點個數可轉化為方程根的個數或兩函數圖像的交點個數。零點存在性定理是判斷函數是否存在零點的一種方法,但要注意其使用的兩個條件,即連續性與異號性。

例13已知定義在R 上的函數y=f(x)的圖像是一條不間斷的曲線,f(a)≠f(b),其中a＜b,設F(x)=f(x)-,求證:函數F(x)在區間(a,b)上有零點。

題型14:函數的實際應用

掌握兩類函數模型:一類是指數型函數模型,通常可表示為y=a(1+p)x(其中a為原來的基數,p為增長率,x為時間),另一類是對數型函數模型,通常可表示為y=mlogax+n(m,n,a為常數,a＞0,a≠1,m≠0)。解決函數應用問題的關鍵是依據實際情況所提供的數據求得相應解析式,然后利用相應解析式解決實際問題。

例142018 年12 月8 日,我國的“長征”三號乙火箭成功發射了嫦娥四號探測器,這標志著中國人民又邁出了具有歷史意義的一步。火箭的起飛質量M是箭體(包括搭載的飛行器)的質量m(t)和燃料質量x(t)之和。在不考慮空氣阻力的條件下,假設火箭的最大速度y(km/s)關于x(t)的函數關系式為y=k[ln(m+x)-]+4ln2(其中k≠0)。當燃料質量為時,該火箭的最大速度為4km/s。

(1)求“長征”三號系列火箭的最大速度y與燃料質量x之間的函數關系式。

(2)已知“長征”三號火箭的起飛質量M是479.8t,則應裝載多少噸燃料才能使火箭的最大飛行速度達到8km/s?(結果精確到0.1t,e取2.718)

解:(1)由題意得4=k{ln[m+·m]-}+4ln2,據此解得k=8,所以所求函數關系為y=8[ln(m+x)-]+4ln2=。

(2)由已知得M=m+x=479.8,則m=479.8-x。由y=8,可得,解得x≈303.3。

故應裝載大約303.3t燃料,才能使火箭的最大飛行速度達到8km/s。

題型15:三角函數的化簡與求值

熟練掌握兩個基本關系式sin2α+cos2α=1及,并能應用兩個關系式進行三角函數的求值、化簡、證明。在倍角公式中,要特別注意cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α及其變形式。誘導公式可概括為的各三角函數值的化簡公式,記憶規律是:奇變偶不變,符號看象限。

題型16:三角函數的圖像與性質

三角函數的性質主要包括定義域、值域、單調性、奇偶性、對稱性、周期性等。對于三角函數的圖像與性質問題,一般先通過恒等變換將函數表達式變形為y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+k的形式,然后將ωx+φ看成一個整體,利用整體代換思想加以解決。畫函數y=Asin(ωx+φ)的圖像的兩種方法:“五點法”和圖像的伸縮與平移變換法。

例16已知函數f(x)=·cosωx在x=處取得最值,其中ω∈(0,2)。

(1)求函數f(x)的最小正周期。

(2)將函數f(x)的圖像向左平移個單位長度,再將所得圖像上各點的橫坐標伸長為原來的3倍,縱坐標不變,得到函數g(x)的圖像。若α為銳角,且g(α)=,求cosα的值。