基于特征聚類優化的KM-FCM-RF算法研究
羅 超,彭玉濤
(井岡山大學網絡信息中心 江西 吉安 343009)
0 引言
在常用的決策樹算法中,最常見的算法是隨機森林算法。隨機森林算法的優點在于通過對數據噪聲的高度容忍度來得到較高預測精確度。Chai[1]將隨機森林算法運用到化工故障分類,提高了故障檢測精度;Cheng[2]在網絡安全方面運用隨機森林算法,極大提升了網絡安全監測正確率;Zafari[3]在化工項目評估管理領域運用隨機森林算法,得到了更加準確的評估預測結果。
在具有明顯優點的同時,隨機森林算法也存在一些缺點,例如對數據集的特點相近似聚類的檢索效率比較低,對數據集的動態聚類數據泛化特征時造成的誤差估值往往比較大。針對這些缺陷,也有很多學者做了大量的研究以改進。王德軍等[4]、劉曙光等[5]、王磊[6]分別采用時間序列特征泛化聚類、遙感數據多時相動態聚類、加權平均泛化數據后聚類的方法,得到了對精度不同程度的提高,并且聚類的效率也得到了相應的改善。對隨機森林算法提出了非常有用的改進和補充。
本文將嘗試采用將特征聚類KM算法與FCM算法相結合,對隨機森林算法進行優化,形成KM-FCM-RF算法優化模型。對多模動態K均值聚類和模糊C均值互相融合與補充的方法,采用對多模動態數據集的特征數據進行聚類,對傳統的隨機森林算法進行優化后,再計算特征優化的差異化DBI的值,重新對DBI序列值進行排序,篩選相關的特征,在聚類多模動態數據時達到提高效率的目的。
1 傳統隨機森林算法
如果研究人員用Ntree表示決策樹中多維特征的數量,OOBi表示第i棵決策樹的多模動態數據的特征數據,ErrOOBi代表的是OOBi中錯誤數據樣本的數量,如果有一個數據集的特征有d個,那么這個數據集可以稱之為數據集D,XJ(j=1,2,…,d)表示該數據特征集的度量,其算法步驟如下:
步驟1:首先基礎得到多霧的樣本數量ErrOOBi的值;
步驟2:置換后,得到了XJ,
再次置換后得到;
步驟3:均值計算得到的值,可以表示為
步驟4:重復以上步驟1到步驟3,執行次數限定為Ntree次,循環結束后可以得到{ErrOOBi,i=1,2,L,Ntree}
步驟5:根據以上兩個輸出結果,可計算粗聚類變化的均值:

則可以認為多模動態數據集的聚類集合就是VI(XJ)。
通過步驟1到步驟5,可以看到隨著多模特征集中特征維度的增加,循環訓練需要更多的時間,結果就必然減緩了訓練速度,進而降低多模數據特征集的訓練效果。本文擬采用高維多模聚類的方法,對以上的算法進行優化改進,已加快訓練速度和提高性能。
2 基于多模高維聚類優化的方法
2.1 聚類方法介紹
將K均值聚類(KM聚類)和模糊C均值聚類結合后,劃分多模動態特征族,排序后進行聚類。優化后得到訓練誤差均值DBI,DBI中最小值的聚類特征則為最終的結果,也是最佳結果。
2.1.1K均值聚類
根據春花等[7]的研究,K均值算法中,多模數據集中數據特征樣本的距離與相似度是反比關系。已知出事聚類和聚類中心,分別用K和C表示,則(C={μi,1≤i≤K})。
迭代計算的步驟為:
步驟1:得到每一個多維動態特征樣本的中心聚類值;
步驟2:重新聚類分簇,并計算DBI。
重復執行步驟1和步驟2,
步驟3:計算誤差平方和(SSE),一直到符合收斂條件。(SSE)的計算公式為:

2.1.2 模糊C均值算法(FCM)
模糊C均值算法主要計算數據集中樣本與聚類中心的關聯隸屬度,來完成對多維特征數據分類[8]。存在多維動態數據集Dn×p,其中的樣本數量為n,隸屬度矩陣U的計算公式為:

再計算每個樣本集聚類中心V,計算公式為:

則J(U,V)可以用下式表示:

||xi-vj||表示樣本各個聚類中心的均值。
2.1.3 離散相關度計算
使用KM和FCM算法對動態多模數據集的特征計算中心差異聚類時,計算出DBI的值,用來表示離散相關度索引的值。利用以下的公式來計算聚類中心最佳值:
(1)均值離散相關隸屬度:

(2)各聚類中心的距離值:
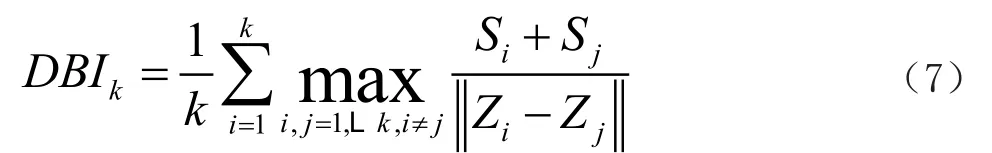
根據樸尚哲等[9]的研究,此時DBI的值為最佳聚類中心的值。
2.2 HDC-RF算法
2.2.1 KM-FCM-RF特征評估算法
對多維數據集進行聚類,并且根據聚類中心值的均值誤差來進行排序。
步驟1:采用傳統隨機森林算法,計算出樣本數據多維特征,并以此為排序的根據。
根據Alon[10]的研究,使用皮爾遜相關性系數ρxy來衡量族內特征與分類信息的相關性。

在上式中,特征x的均值用Zx來表示,特征y的均值則用Zy來表示,
ρxy表示皮爾遜相關系數,系數越大,則表示數據集特征之間具有越大的相關程度。
步驟2:根據閾值δ,篩選出相關系數ρxy>δ的高維特征。本文改進的閾值δ計算公式表示為:

根據式(9)計算出多維動態數據集特征,采用排序的規則為簇內優先、簇間其次。最終,計算得出了多維動態數據集的特征簇序列。
2.2.2K均值和C均值優化的隨機森林算法流程
在以上算法的基礎上,將K均值C均值優化的隨機森林算法優化流程用下圖1表示。
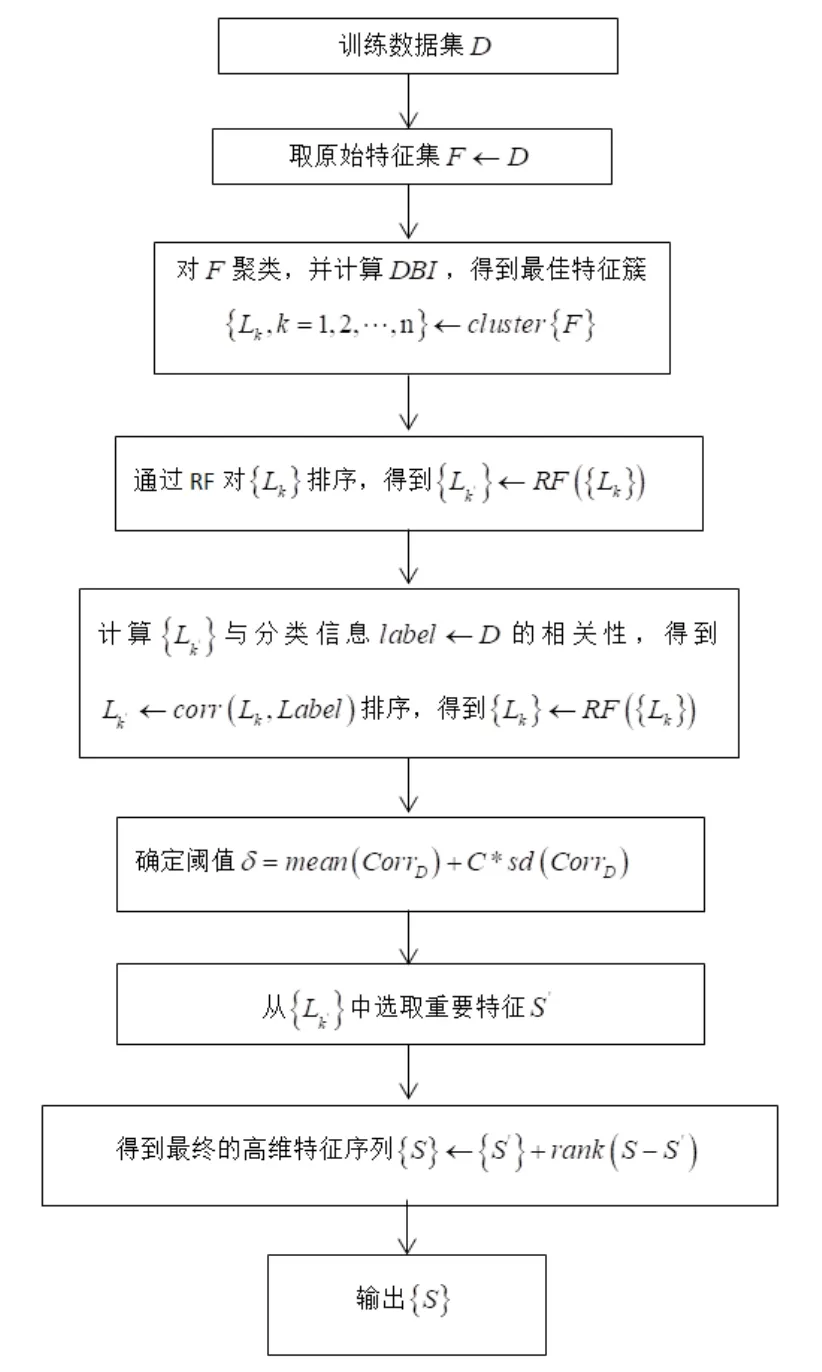
圖1 算法流程圖
3 實驗分析
3.1 實驗準備
采用Alon等[10]和Golub等[11]提供的高維多模動態特征數據集作為輸入的樣本數據集。輸入之前,先將數據和特征清除冗余,最終數據表征如下表1所示:

表1 實驗數據集
根據表1的結果可以看出,多個高維特征數據集差別不大時,KddCup99由于具有更小的特征數,可以更方便地對數據集中的少量非高位數據集進行特征提取,并進行輸出對比。反之,Minst則由于具有更多的特征數和更高維度,更適用于高維數據集的特征提取和對比。
在進行仿真實驗時,決策樹采用的是具有200個決策樹的C4.5基本分類器,并將其最佳聚類范圍設置為實驗結果的預測閾值評價采用ACC標準。如果閾值越大,則算法的優化效果越好、聚類數據集的性能就越高。
3.2 實驗結果
將本文的優化算法與傳統的隨機森林算法分別運行在KddCup99和Minst數據集進行比較,為了得到更穩定的結果,將算法運行30次的均值作為最終結果。實驗結果對比如下圖2、圖3所示:

圖2 KddCup99中KM-FCM-RF、RF預測精度對比

圖3 Minst中KM-FCM-RF、RF預測精度對比
根據以上兩圖可以得到如下結論:
(1)根據圖2的結果可知,在KddCup99的中低維數據集訓練中,KM-FCM-RF算法在前200個樣本時,預測精度略比RF略小,但從2 000個樣本開始,預測精度一直高于傳統RF算法。
(2)圖3表明,在Minst的高維數據集上的訓練過程中,KM-FCM-RF的精度自始至終都比傳統RF算法高。
4 結論
針對傳統的隨機森林算法在多維特征數據集預測精度不高,本文提出了一種基于K均值和C均值優化聚類的隨機森林算法,即在對多維特征數據集樣本聚類后,集合K均值模糊C-均值算法結合,計算得到DBI指標并對該指標排序后,進一步得到的閾值δ比較,最終得到多維特征數據集的特征序列。實驗結果表明,經過本文優化后基于K均值和C均值優化聚類的隨機森林算法,具有更好的聚類效果、預測精度更高,具備良好的可行性。

