基于技術成熟度的確信可靠性分配方法

陳志聰, 康 銳, 祖天培, 張清源

(1. 北京航空航天大學可靠性與系統工程學院, 北京 100191;2. 北京航空航天大學云南創新研究院, 云南 昆明 650051;3. 北京航空航天大學航空科學與工程學院, 北京 100191)

0 引 言

可靠性分配是一項重要的可靠性工程活動,它將系統的總體可靠性指標要求自上而下、由整體到局部分配給組成單元,以保證系統滿足設計要求。因此,系統總體可靠性指標要求采用何種可靠性度量方法對可靠性分配工作有著至關重要的影響。傳統的可靠性度量以概率論為基礎,認為可靠度是產品在規定時間內和規定條件下完成規定功能的概率。根據大數定律,概率是極限頻率,這就意味著工程中如果想要驗證相應的可靠度指標,就需要進行大量的統計試驗,否則就不能得到可信的結果。換而言之,基于概率測度的可靠性度量方法僅適用于具有充足可靠性數據信息的工程場景。然而,在工程實踐中,由于成本、進度等方面的限制,有些產品,特別是新研產品,其可靠性數據信息是非常有限的,無法驗證概率測度下分配的可靠性指標要求。因此,僅僅以概率測度作為可靠性度量并不能滿足可靠性工程實踐的需求。

為解決上述問題,本文擬研究基于確信可靠度的可靠性分配方法。確信可靠度是由北京航空航天大學康銳教授提出的一種全新可靠性度量,是確信可靠性理論的核心。這一可靠性度量以概率測度、不確定測度和機會測度3大數學測度為基礎,可以解決大樣本、小樣本以及兩種情況混合的各類可靠性度量問題。近些年來,確信可靠性理論圍繞確信可靠度,發展了確信可靠性設計、分析、評價、優化等各類方法。

確信可靠性理論認為實際系統是不確定隨機系統,受到隨機不確定性與認知不確定性的共同影響,其確信可靠性利用機會測度來度量。其中,隨機不確定性是指客觀世界固有存在的不確定性,是不可消除的;認知不確定性是指由于信息缺乏、知識缺失所造成的不確定性,是可以隨著信息的累積、知識的增加而逐漸減少的。在系統確信可靠性分析中,一般認為組成單元受單一不確定性的影響分為兩類:① 主要受隨機不確定性影響的單元稱為隨機單元,這類單元通常有較多可靠性數據,可用概率統計方法來分析其確信可靠性,即隨機單元的可靠度采用概率測度;② 主要受認知不確定性影響的單元稱為不確定單元,這類單元的可靠性數據呈現小樣本特征,需用不確定統計方法來分析其確信可靠性水平,即不確定單元的可靠度采用不確定測度。確信可靠性理論針對不同類別的單元采用不同度量方法,可極大提高可靠性指標評價結果的合理性和可信性。因此,基于確信可靠度開展可靠性分配工作可以有效解決小樣本條件下單元概率可靠度指標無法驗證的問題。

綜合來看,確信可靠性分配方法包含兩大重要任務:一是對單元類別進行劃分,為單元選擇適用的可靠性測度;二是構建可靠性分配優化模型,以獲得效費比最佳的分配方案。針對這兩個問題,本文提出了基于技術成熟度的確信可靠度分配方法。技術成熟度是由美國航空航天局提出的一種技術完善程度的一致性度量,用技術成熟度等級(technology readiness level,TRL)來表征,眾多工業領域和政府組織分別提出了各自的技術成熟度等級評價標準。技術成熟度等級從低到高依次描述了技術從概念報告到成功應用的發生發展歷程,代表了技術在各個發展階段已經實施的各項工程活動。技術成熟度等級較好地滿足了確信可靠性分配需求:一方面,技術成熟度等級越高,該技術所經歷的工程活動越多,研究人員積累的知識和相關經驗越豐富,對該技術的認知不確定性越小,因此可以將技術成熟度等級作為單元分類的標準,對不確定隨機系統中各單元的可靠性測度類別進行判定;另一方面,提高不同技術成熟程度水平下的單元所消耗的機會成本是不同的,技術成熟程度越高的單元實現可靠度賦值要求的機會成本越低,因此可以基于技術成熟度評分構造單元可靠性機會成本函數,作為單元可靠度賦值的限制條件,進而實現資源有限情況下系統確信可靠度的最優分配。

綜上,本文將以確信可靠性理論作為理論基礎,以技術成熟度為工具,提出一套適用于不確定隨機系統的確信可靠度分配方法,以填補確信可靠性分配方法的空白。

1 確信可靠性理論基礎

確信可靠性理論是在認知系統確定性行為規律的基礎上量化不確定性從而解決可靠性工程問題的一種全新的可靠性理論。確信可靠性理論認為實際系統是受隨機不確定性和認識不確定性的共同影響的不確定隨機系統,并將不確定理論和機會理論引入可靠度的數學表征方法中,提出了“確信可靠度”這一全新的可靠性度量。

確信可靠度是指不確定隨機系統在規定時間內、規定條件下完成規定功能的確信程度。其數學表述為:設不確定隨機系統的狀態變量為,確信可靠域為,則確信可靠度為狀態變量位于確信可靠域Ξ中的機會,即

()=Ch{∈Ξ}

(1)

在這個定義中,可靠性定義中的規定時間體現在確信可靠度函數中()的上,不同的規定時間下對應著不同的確信可靠度;規定條件體現在狀態變量上,不同的條件將對應不同可靠性度量空間中的映射關系;規定功能體現在確信可靠域Ξ,不同的功能要求對應不同的可靠域。在此基礎上,機會測度實現了對所有這些因素的各類不確定性的測量,并與上述三者共同構成了確信可靠度定義的全部元素。

不確定隨機系統存在兩種退化形態,即隨機系統和不確定系統,相應地,其數學測度會發生變化。隨機系統主要受隨機不確定性的影響,其測度由機會測度退化為概率測度,確信可靠度記為

()=()=Pr{∈Ξ}

(2)

式中:()主要表示基于概率論的確信可靠度,即傳統概率可靠度,它表征系統可靠的頻率。

不確定系統主要受到認知不確定性的影響,因此測度從機會測度退化為不確定測度,此時,確信可靠度記為

()=()={∈Ξ}

(3)

式中:()主要表示基于不確定理論的確信可靠度,用于表征系統可靠的信度。

當進一步考慮產品的層次關系時,可以將產品分成系統、子系統、單元3個層次。確信可靠性理論一般認為組成單元受單一不確定性的影響:主要受隨機不確定性影響的單元稱為隨機單元;主要受認知不確定性影響的單元稱為不確定單元。由隨機單元組成的子系統稱為隨機子系統,由不確定單元組成的子系統稱為不確定子系統。

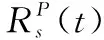
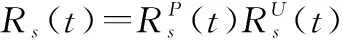
(4)

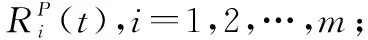
(5)

對于上述可拆分為隨機子系統和不確定子系統的不確定隨機系統,我們稱之為簡單不確定隨機系統。相應地,對于不能直接拆分為不確定子系統和隨機子系統的不確定隨機系統,稱之為復雜不確定隨機系統。文美林和康銳提出了由不確定單元和隨機單元的可靠度計算復雜不確定隨機系統的系統可靠度的方法。

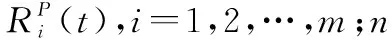
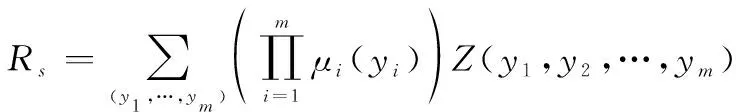
(6)

其中,

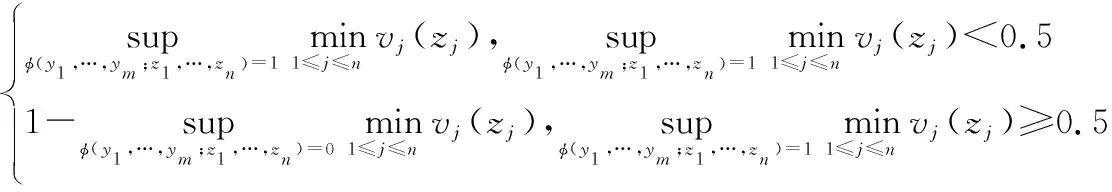
從定理2中可以看出,復雜隨機不確定系統的系統可靠度計算不但涉及概率測度和不確定測度兩種測度,且包含復雜的數值運算。這就為系統可靠度分配帶來了極大的挑戰。因此,本文基于技術成熟度提出了系統確信可靠度的分配方法,以期推動確信可靠性理論的工程應用。

2 方法概述

本文所期望的分配方案是以盡可能低的成本保證系統指標在允許的微小范圍內恰好滿足設計要求,實質上是一個優化設計問題,最簡單的思路是依據可靠性提升成本的高低來對單元可靠度賦予相應的數值要求。如果有成本關于可靠性的真實數據,可以擬合出二者之間的定量關系,但實踐中往往缺乏相關數據,這就需要選擇合適的指標來刻畫二者之間的關系。通常來說,某個單元的技術成熟度越高,對其了解和應用程度越高,則對其賦予高可靠度的實現難度越低,機會成本也相對較低。因此,本文選擇技術成熟度作為劃分單元類別以及構造成本函數的依據。總的來說,基于技術成熟度的確信可靠度分配流程如圖1所示。

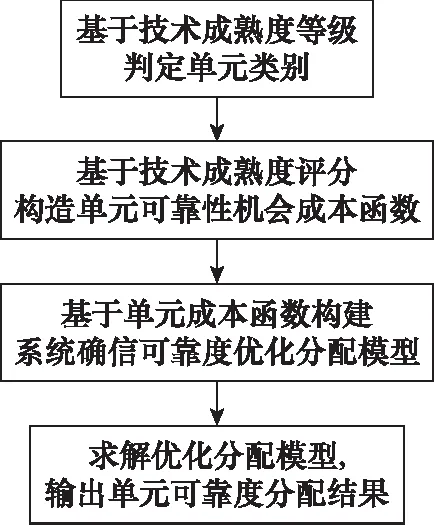
圖1 基于技術成熟度的系統確信可靠度分配流程圖Fig.1 Flow chart of system belief reliability allocation based on technology readiness

該方法主要包括以下4個步驟。

基于技術成熟度等級判定單元類別

判定單元類別是系統確信可靠度分配的首要環節。只有厘清單元類別,確定單元適用的可靠性測度,才能對單元的確信可靠度提出科學合理的賦值要求。本文提出一種將技術成熟度等級評價流程與單元可靠性信息量的充足程度相結合的邏輯決斷方法,用以判斷單元可靠性測度、劃分單元類別。

基于技術成熟度評分構造單元可靠性機會成本函數

構造各單元的可靠性機會成本函數是構建系統確信可靠度優化分配模型的基礎。機會成本函數可以描述與系統內其他單元相比,某單元為實現可靠度賦值要求所付出機會成本的相對高低。在現有技術成熟度等級判定方法的基礎之上,本文創新性地提出技術成熟度評分的獲取方法,并利用其構造單元可靠性機會成本函數。

基于單元成本函數構建系統確信可靠度優化分配模型

為實現系統確信可靠性指標要求的科學分配,本文構建起系統確信可靠度優化分配模型。該模型以總機會成本最小化作為目標,以系統和單元確信可靠度的取值范圍作為約束,完成從系統可靠性指標要求到單元可靠性賦值要求的合理分配。

求解優化分配模型,輸出單元可靠度分配結果

步驟 3通過數學建模,將系統確信可靠度的分配問題轉化為優化分配模型的求解問題。相應地,本步驟通過求解該優化分配模型獲得單元可靠度分配結果,輸出滿足要求的系統確信可靠性分配方案。

3 基于技術成熟度等級的單元類別判定

要對系統開展確信可靠性分配工作,一項重要的工作是判定單元類別,即確定單元確信可靠性度量采用的數學測度。本節首先引入工程界判斷技術發展狀態的一個重要尺度——技術成熟度,隨后將單元的技術成熟度等級與可靠性信息量的充足程度相結合,給出單元類別的邏輯決斷圖,以完成單元類別的判定工作。

3.1 技術成熟度

技術成熟度等級是用于衡量技術成熟程度的尺度。包括美國航空航天局、美國國防部、美國能源部、歐盟、國際標準化組織以及中國總裝備部在內的組織和機構均研究制定了技術成熟度評價標準規范,雖然上述標準的具體內容有所差異,但大體上都包括了技術成熟度等級的定義及判定條件等內容。新技術要投入應用需要經歷由實驗室到工程化、再到產業化3個階段。在實驗室階段(TRL1～TRL3),研究人員側重于原理和概念方面的研究,旨在推動高新技術盡快進入實用階段。在工程化階段(TRL4～TRL6),研究人員要對產品原型進行由實驗室環境到相關環境的驗證,并解決工業化生產可能面臨的技術問題。在產業化階段(TRL7～TRL9),研究人員逐步完成了系統在典型使用環境中的驗證使用乃至在真實環境中的實際應用。此處結合GJB 7688—2012與GB/T 37264—2018的相關規定,簡單介紹各個等級的技術成熟度水平和相對應的發展階段,如圖2所示。

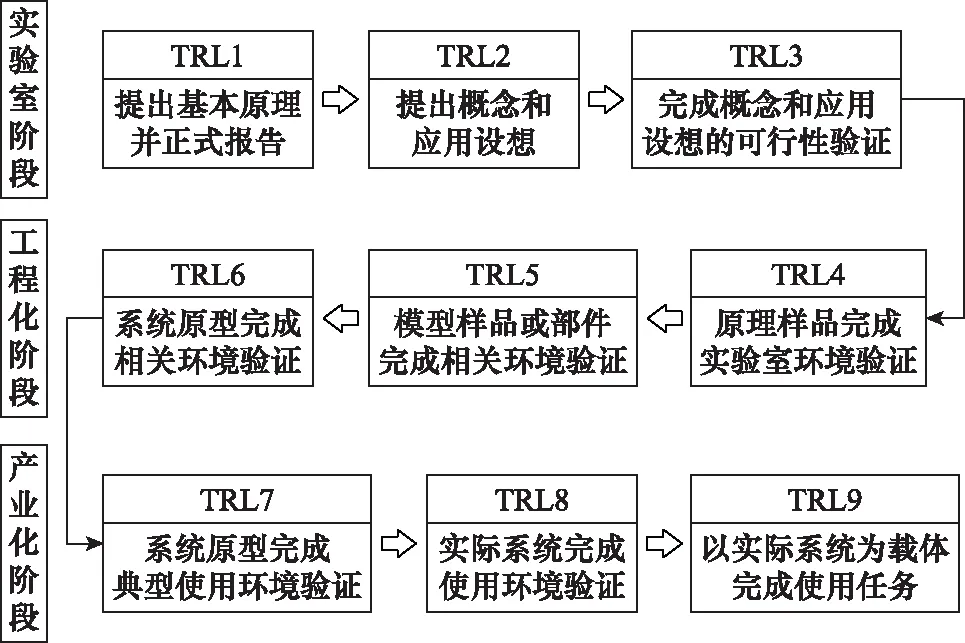
圖2 技術成熟度等級和所屬發展階段Fig.2 Technology readiness level and development stage

產品在進入產業化階段之后才開始大量產生與可靠性相關的信息,而大量可用的可靠性信息正是采用概率測度評價單元可靠性的基礎。因此,本論文以TRL7為關鍵決斷條件構建了基于技術成熟度等級的單元類別邏輯決斷流程圖。

3.2 單元類別判斷邏輯決斷圖

GJB 7689—2012規定,當某項技術滿足等級規定的全部條件,而不滿足等級+1規定的全部條件時,判定其技術成熟度等級為。本文結合GJB 7689—2012給出的技術成熟度等級評價流程以及可靠性信息量,建立起圖3所示的邏輯決斷流程圖,來判定各個單元可靠性度量適用的測度,輸出單元所屬類別的判定結果。如圖3所示,如果某個單元的關鍵技術成熟度等級≥7(即進入了產業化階段),且可靠性信息足夠獲得可靠性的概率測度,則該單元可靠性度量采用概率測度,被判定為隨機單元;否則該單元可靠性度量采用不確定測度,被判定為不確定單元。需要特別說明的是,工程界通常以樣本量是否超過30作為信息充足與否的分界線,但具體應用時可結合研究對象的實際需求進行相應增減。

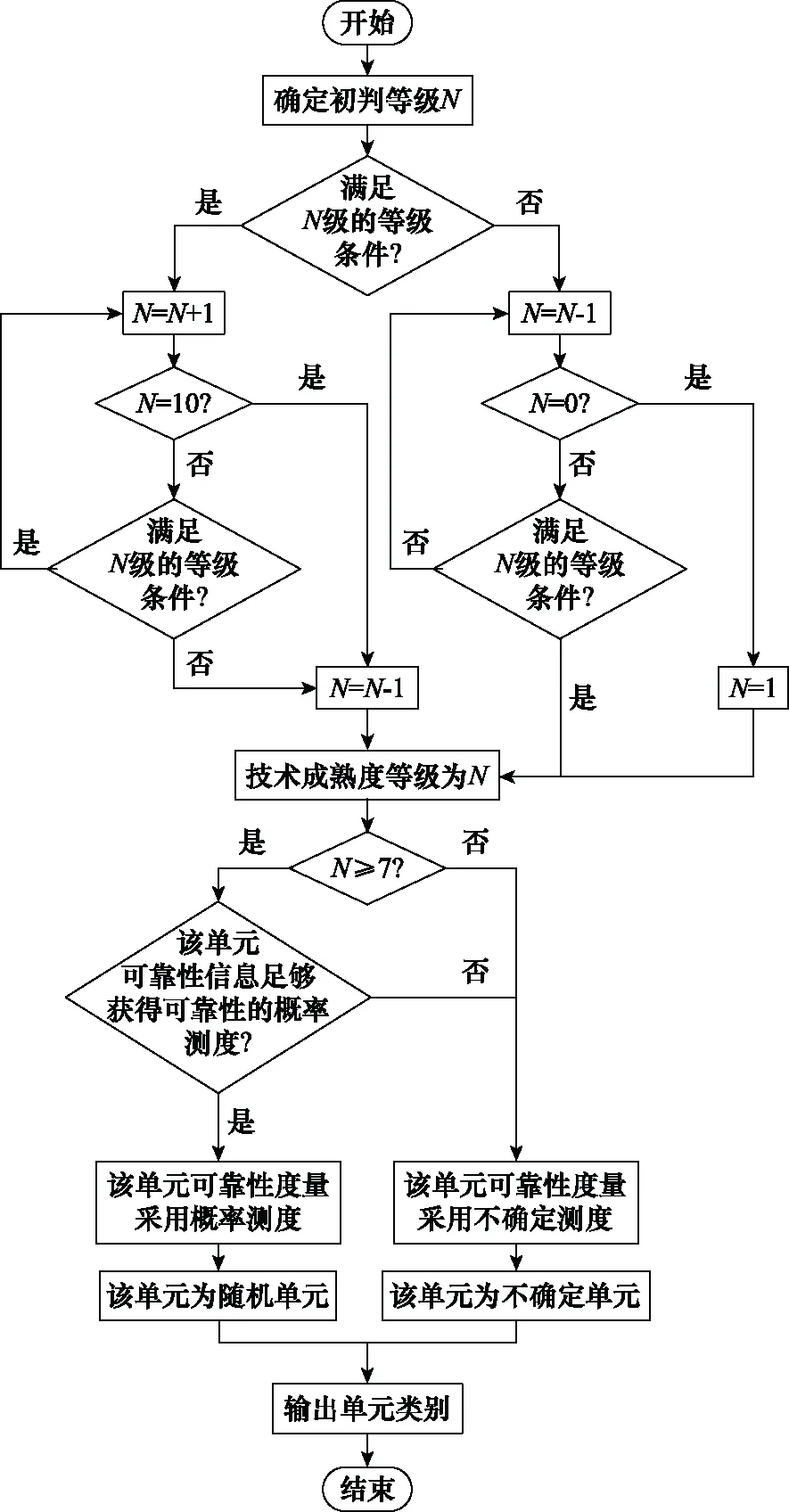
圖3 單元類別的邏輯決斷流程Fig.3 Logical decision flow of unit category

4 基于技術成熟度評分的單元可靠性機會成本函數構造

本節首先給出了技術成熟度評分的概念及其確定方法,繼而提出了基于技術成熟度評分的單元可靠性機會成本函數的構造方法。

4.1 技術成熟度評分確定方法

作為技術成熟程度的衡量尺度,技術成熟度等級通過該技術是否滿足全部等級條件來判定,對于每項條件只有滿足和不滿足兩種判斷結果,卻沒有考慮具體條件的實現情況。為了全面考慮所處等級以及等級條件實現情況對于技術成熟程度的影響,以綜合體現技術成熟程度對于可靠性分配的影響,本節從某單元關鍵技術所處等級和等級的具體表現著手,給出技術成熟度的綜合評分。技術成熟度評分的獲取流程如圖4所示。

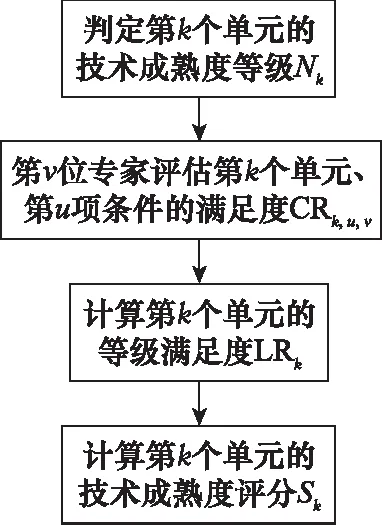
圖4 技術成熟度評分的獲取流程Fig.4 Flow of obtaining technology readiness score

接下來,按技術成熟度評分的獲取步驟來詳細介紹圖4中涉及到的具體參數。

4.1.1 判定技術成熟度等級

技術成熟度等級是用于衡量技術成熟程度的尺度。∈{1,2,…,9},值的確定參照第2.2節。技術成熟度所處等級越高,表明研究人員對于該項技術的了解和應用程度越高。

4.1.2 評估條件滿足度

現有的技術成熟度等級評價工作只通過是否滿足規定的全部條件來判定技術所處等級,卻并不關心各項條件的具體實現情況。也就是說,只有0(不滿足某項條件)和1(滿足某項條件)的區別,勉強滿足某項條件與遠遠超過該條件的要求都表示為1,并不能體現出二者的區分度。

為評價某項技術所處成熟度等級對應各項條件的具體滿足情況,本文利用對條件滿足度(condition satisfaction rate, CR)的專家評分來衡量某一等級某項條件的具體完成程度。CR∈(0,1],評分越高說明單元在該等級條件上表現越好。若CR→0,說明單元勉強滿足該項條件的要求;若CR=1,說明單元完全滿足甚至可能是遠遠超出該項條件的要求。

4.1.3 計算等級滿足度

等級滿足度(level satisfaction rate, LR)是衡量技術在特定成熟度等級下表現的指標,綜合考量該等級對應的全部條件的滿足情況。

設第個單元(=1,2,…,)的技術成熟度等級為,該等級對應的等級條件共有項,邀請位專家對各項條件的滿足度進行評分。記CR,,為第位專家對第個單元的第項條件(=1,2,…,;=1,2,…,)的條件滿足度評分,則第個單元的等級滿足度為

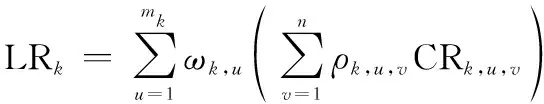
(7)

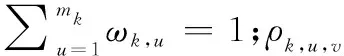
易知,LR∈(0,1],且取值越大,說明技術在該等級上表現越好。若LR→0,說明第個單元剛剛達到等級的條件要求;若LR=1,說明第個單元在等級的各項條件上幾乎沒有提升的余地。

(1) 計算專家權重

專家權重,,是根據專家與專家組意見的一致程度給出的權重賦值,即某位專家與專家組意見越一致,其給出的評分越重要,專家權重越高。

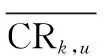
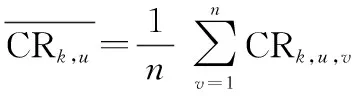
(8)

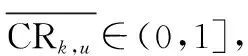
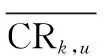
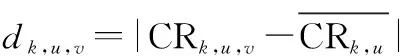
(9)

由式(9)易知,,,∈(0,1],且取值越小,說明第個專家對第個單元的第項條件的滿足度評分與專家組的平均評分偏差越小。

根據偏差,,,可給出第位專家對于第個單元的第項條件(=1,2,…,;=1,2,…,;=1,2,…,)的滿足度評分的專家權重為

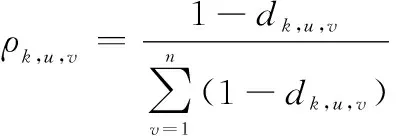
(10)

由式(10)易知,,,∈(0,1),且與專家組平均評分偏差越小的專家評分的權重越高。

(2) 計算條件權重

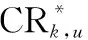
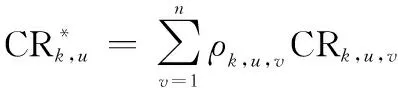
(11)

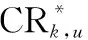
設,為第個單元的第項條件(=1,2,…,;=1,2,…,)的條件權重,則其計算公式為

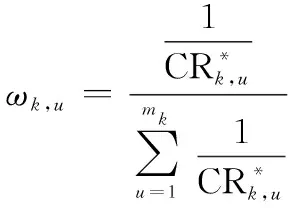
(12)

由式(12)易知,,∈(0,1),且加權條件滿足度越小的條件的權重越高。

414 計算技術成熟度評分

技術成熟度評分是衡量某一技術在發展周期內成熟程度的綜合指標。第個單元(=1,2,…,)的技術成熟度評分為

=+LR

(13)

與目前的等級評價工作相比,公式得到的評分可以更為全面地衡量第個單元的技術成熟程度,其中前半部分與單元關鍵技術所處等級有關,后半部分與等級評分LR有關。易知,技術成熟度評分∈[1,10],且值越大,說明研究人員對該技術的了解和應用程度越高,實現單元可靠度賦值的難度越低。若=10,說明該單元不只是技術成熟度等級到達了,各項條件的實現情況也趨于完美。

4.2 單元基礎機會成本系數確定方法

單元基礎機會成本系數描述的是與系統內其他單元相比,提升某單元可靠性的機會成本的相對高低程度。對第個單元(=1,2,…,)的基礎機會成本系數采用10分制打分的處理方法,分值越高說明相對于其他單元而言該單元實現可靠度賦值要求所需要付出的成本越高。各單元基礎機會成本的評分準則如表1所示。

表1 單元基礎機會成本的評分準則

4.3 單元可靠性機會成本函數的構造

可靠性機會成本描述的是將單元可靠度由當前水平提升到特定要求時所需要付出的人力、物力、財力等資源,而不考慮前期為實現當前可靠度水平已經投入的資源。單元可靠性機會成本函數刻畫了資源投入量與單元可靠度提升量之間的定量關系。

4.3.1 構造形式

本文構造了一種基于技術成熟度評分的單元可靠性機會成本函數,來描述第個單元(=1,2,…,)的可靠度賦值為(即由0提升到)所付出的機會成本,為

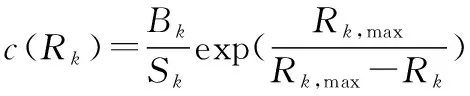
(14)

式中:為第個單元的基礎機會成本系數;為第個單元的技術成熟度評分;,max為第個單元的可靠度極限值;為分配至第個單元的可靠度賦值要求。需要注意的是,對于特定的第個單元而言,為變量;、和,max為常數,且∈[1,10],∈[1,10],與的獲取分別見第41和第42節,,max的獲取將在第432節中介紹。

該函數有如下性質:

(1) 機會成本函數具有非負性。由>0,>0,exp(,max,max-)>0,可知()>0,提升單元可靠度水平一定要付出機會成本。因此,機會成本是非負的。

(2) 機會成本函數是關于單元基礎機會成本系數的單調遞增函數。對單元基礎機會成本系數求偏導,可得??=1exp(,max,max-)。易知??>0,當單元的技術成熟度評分、可靠度極限值,max和可靠度賦值要求的取值固定時,基礎機會成本系數越高的單元實現可靠度賦值要求需要付出的機會成本越高。

(3) 機會成本函數是關于單元技術成熟度評分的單調遞減函數。對單元技術成熟度評分求偏導,可得??=-()exp(,max,max-)。易知??<0,當單元的基礎機會成本系數、可靠度極限值,max和可靠度賦值要求的取值固定時,技術成熟度評分越高的單元實現可靠度賦值要求的能力越強,付出的機會成本越低。

(4) 機會成本函數關于單元可靠度賦值單調遞增。對單元可靠度賦值要求求偏導,可得??=,max·(,max-)exp(,max,max-)。易知??>0,對于特定單元來說,其可靠度賦值要求越高,付出的機會成本越高。

(5) 機會成本函數關于單元可靠度賦值的導數為單調遞增函數。對求二階偏導,有??()=,max·(3,max-2)(,max-)exp(,max,max-)。易知??()>0,對于特定單元來說,隨著可靠度賦值要求的提高,每提高單位可靠度所付出的機會成本也會增加。

(6) 當單元可靠度賦值要求→0時,所付出的機會成本()→0,即提升低可靠度單元所付出的機會成本非常低。

(7) 當單元可靠度賦值要求→,max時,所付出的機會成本()→∞,即提升高可靠度單元所付出的機會成本非常高。

432 單元極限可靠度確定方法

,max刻畫了當前技術水平下個單元(=1,2,…,)可以達到的極限可靠度。理想狀態下,,max=1,但由于經濟和技術水平的限制,極限可靠度很難達到1。本文將基于串聯假設得到的各單元可靠度預分配值作為其可靠度極限值,因此極限可靠度可以看作單元可靠性在某些因素影響下的相對數值,而非絕對數值。具體的預分配是分2個階段進行的。

(1) 系統到子系統的確信可靠度預分配

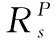
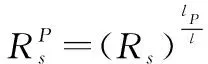
(15)

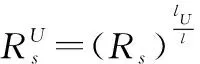
(16)

(2) 子系統到單元的確信可靠度預分配

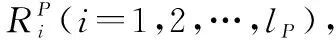
表2 單元可靠度分配相關參數

根據上述預分配過程,可以得到第個單元(=1,2,…,)的確信可靠度極限值為

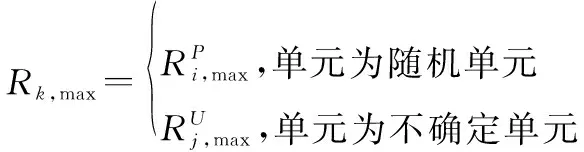
(17)

5 系統確信可靠度優化分配模型

本節首先確定了系統確信可靠度優化分配模型的基本形式,其次,介紹了模型中具體參數的獲取方法;最后給出了優化分配模型的求解算法。

5.1 基本形式

假設各單元之間是相互獨立的,系統和單元只有正常和失效兩種狀態,系統的總機會成本是各單元的機會成本之和。本文以系統的總機會成本最小化為目標,以系統確信可靠度在允許范圍內滿足目標要求且各單元可靠度在規定范圍內取值為約束,構造如下形式的系統確信可靠度優化分配模型:

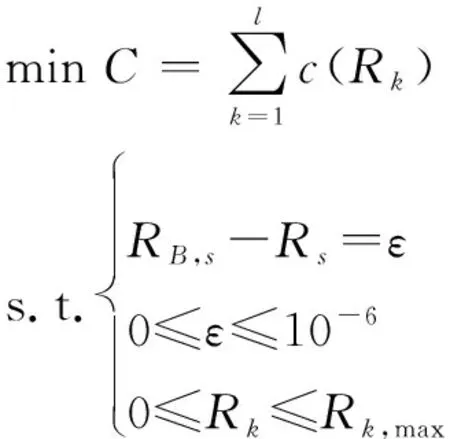
(18)

式中:為系統的總成本;為系統中單元的個數;為分配至第個單元的可靠度要求;()為第個單元的可靠性機會成本函數;,max為第個單元的極限可靠度;,為由分配至第個單元的可靠度計算出的系統的確信可靠度;為系統確信可靠度的設計要求;為系統確信可靠度超出設計要求的允許范圍。

5.2 模型中參數的說明和計算方法

第51節構造的優化模型中,需要另外計算確定的參數有兩類。第一類是與機會成本函數相關的參數,其獲取方式見第4節;第二個是系統確信可靠度,,將,與設計要求進行比較,可以判斷分配方案能否滿足設計任務書規定的要求。

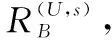
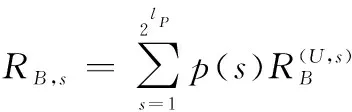
5.3 模型的求解方法

由式(18)易知,系統確信可靠度的優化分配問題為多變量有約束非線性規劃問題。

為實現問題的求解,本文根據單元評分分配因子的相對關系,以某一隨機單元或不確定單元為基準,將所有隨機單元或不確定單元的可靠度折算為用該單元可靠度表述的形式。因此,模型式(18)轉化為含有兩個優化變量的中等規模優化問題,可以用序列二次規劃(sequential quadratic programming,SQP)算法來求解。SQP是目前處理中、小規模非線性規劃問題最優秀的算法之一。SQP算法主要的計算在于求解二次規劃問題QP(,)

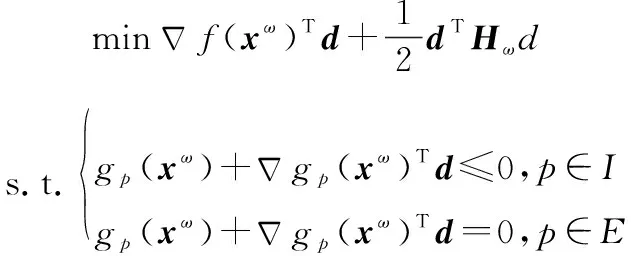
的解,以產生主搜索方向。

對于模型式(18)所示的非線性規劃問題,SQP算法的一般格式如下:

給出初始點,初始對稱矩陣,令=0;

在處求解二次規劃問題QP(,)的解,若=0則停止;

令+1=+(為步長);

修正使得+1保持正定;

令=+1,返回步驟2。

總的來說,本文通過構建系統可靠性優化分配模型將系統可靠性指標的優化分配問題轉化成了非線性規劃問題,利用SQP算法將復雜的非線性規劃問題轉化為一系列較為簡單的二次規劃問題,該優化模型的最優解即為所求的系統確信可靠度分配方案。

6 算 例

本文以雙燃料供氣系統為例,展示基于技術成熟度的確信可靠性分配方法的一般過程。

考慮到優化能源結構、保護環境的實際需求,船舶使用液化天然氣(liquefied natural gas, LNG)和柴油兩種燃料來提供動力,被稱為LNG/柴油雙燃料供氣系統。該系統由LNG儲罐、儲油罐、濾清器、減壓器、汽化器、電子流量計、混合器、電磁噴射閥、發動機等共11個單元組成。其可靠性框圖如圖5所示。

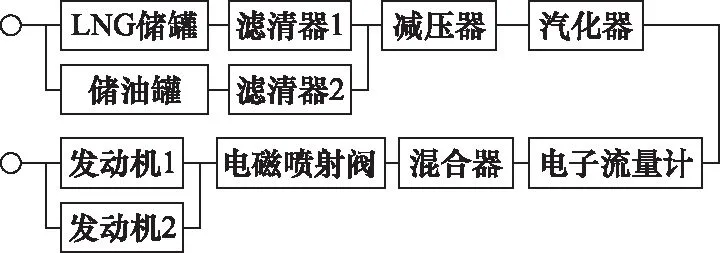
圖5 LNG/柴油雙燃料供氣系統的可靠性框圖Fig.5 Reliability block diagram of LNG/diesel dual fuel gas supply system

為保證該雙燃料供氣系統在實際應用中能夠正常工作且滿足維修要求,一般要求其確信可靠度為=0.8。本節將對這一系統級指標開展分配。

6.1 基于技術成熟度劃分單元類別

按照圖3所示的流程,由專家對單元關鍵技術的成熟度等級進行打分,再結合故障信息的數據量判定單元所屬類別,如表3所示。由表3可知,該系統中濾清器、減壓器、汽化器、電子流量計被判定為隨機單元,LNG儲罐、儲油罐、混合器、電磁噴射閥和發動機被判定為不確定單元。即隨機單元的個數為=5,不確定單元的個數為=6。對劃分完類別的單元進行標號,并標注其各自的可靠度數值要求,如圖6所示。

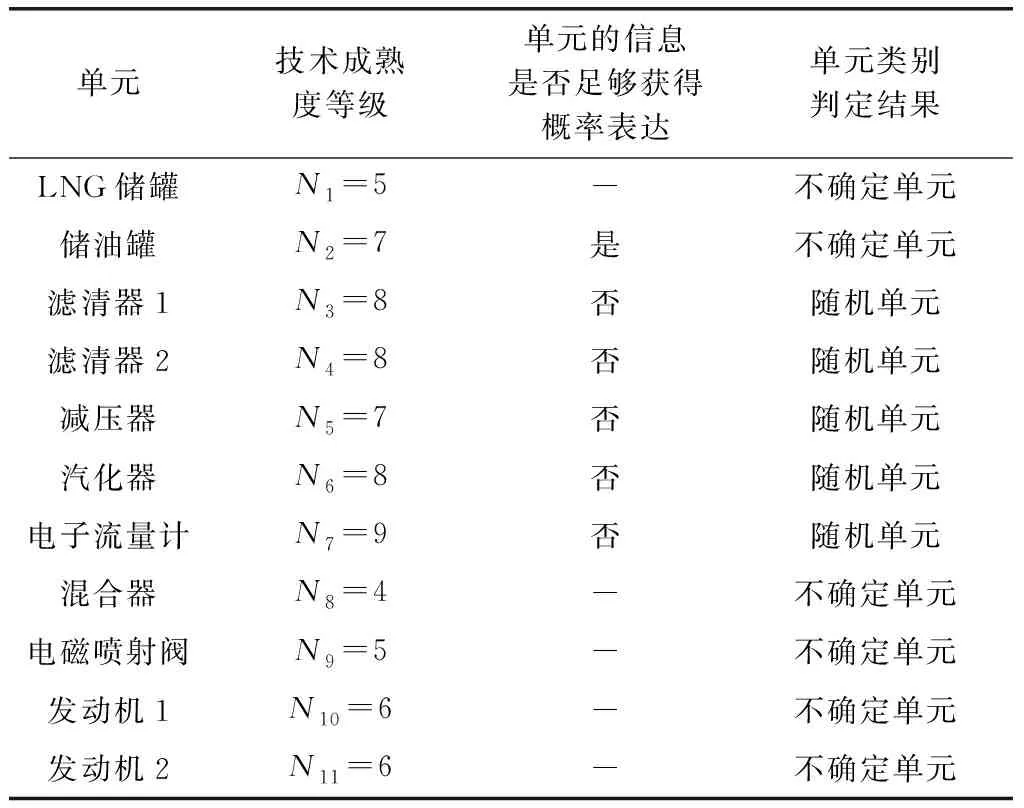
表3 單元類別劃分的相關信息

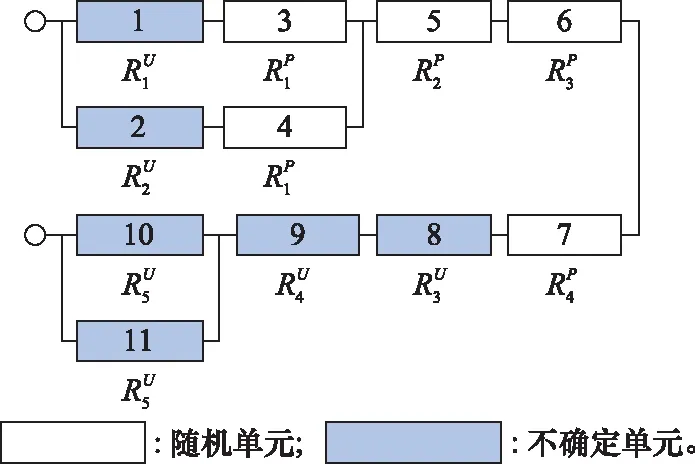
圖6 判定類別后的可靠性框圖Fig.6 Reliability block diagram after classification

6.2 基于技術成熟度評分構造單元可靠性機會成本函數

6.2.1 計算技術成熟度評分

綜合技術成熟度等級及相應的等級評分,計算各單元的技術成熟度評分(在此略去條件質量的原始數據),相關信息如表4和表5所示。

表4 隨機單元技術成熟度評分的計算過程

表5 不確定單元技術成熟度評分的計算過程

622 確定單元基礎機會成本系數

由專家給出對于各單元基礎機會成本系數的評分,如表6所示。

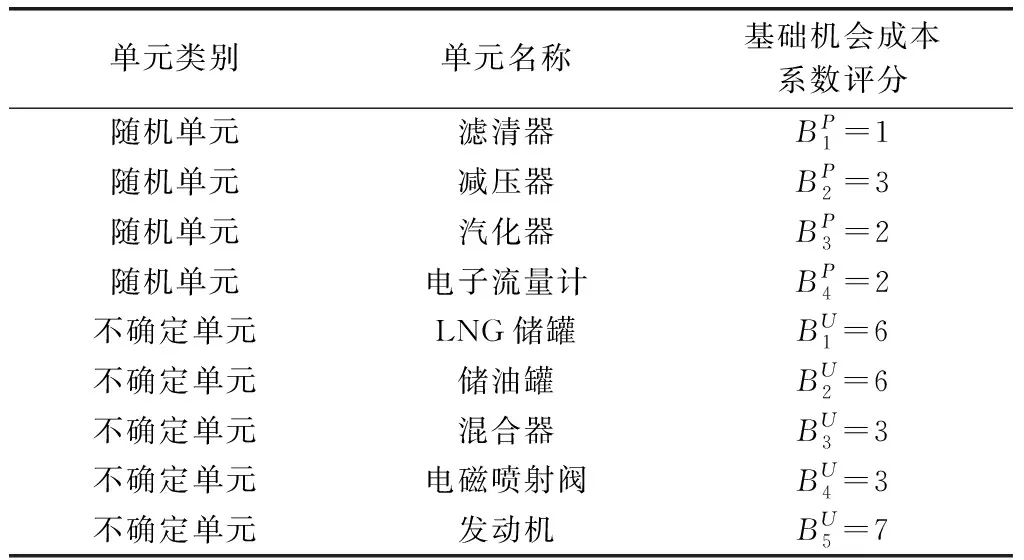
表6 基礎機會成本系數評分

623 確定單元可靠度極限值

假設該雙燃料供氣系統的隨機子系統和不確定子系統為串聯連接,其內部組成單元之間也為串聯連接。首先,將系統的確信可靠度要求分配給隨機子系統和不確定子系統,分別為

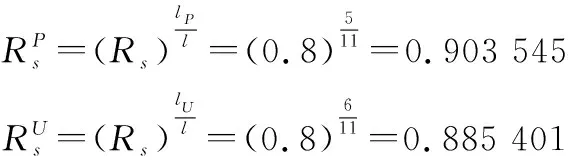
然后,由各組成單元的技術成熟度評分(見表4和表5)以及基礎機會成本系數評分(見表6)得到相應的評分分配因子,根據表2中的極限可靠度計算公式將子系統的可靠度要求分配給其內部的組成單元,相關參數和步驟如表7所示。

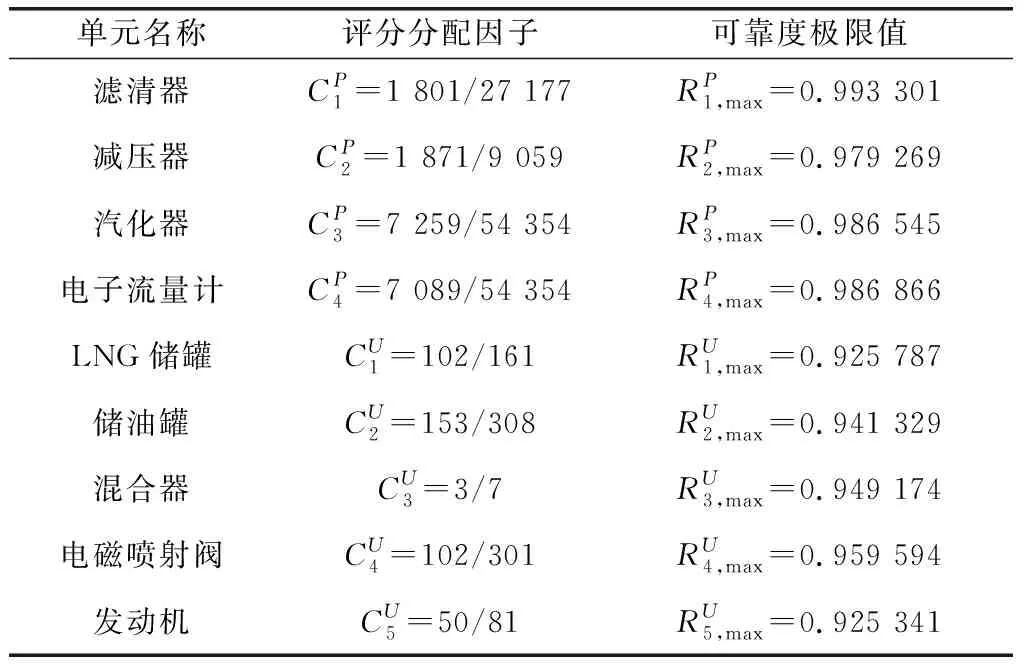
表7 單元可靠度極限值的計算

624 構造單元可靠性機會成本函數

根據上述已經獲得的信息,構造各單元的可靠性機會成本函數,如表8所示。

表8 單元可靠性機會成本函數

6.3 構建系統確信可靠度優化分配模型

根據上述計算和預分配,可以構造該系統確信可靠度分配的優化模型。目標函數為

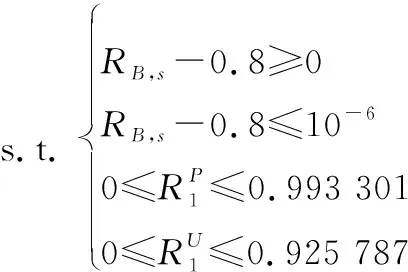
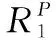
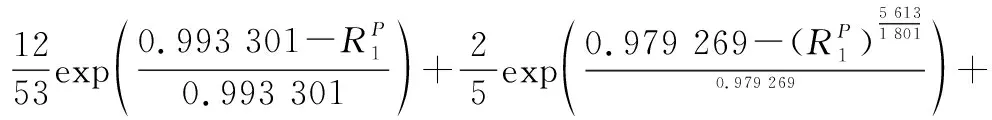
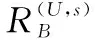
表9 分解算法求系統確信可靠度的過程

根據前文所述,可得系統的確信可靠度為

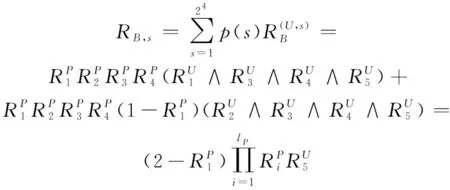
同樣地,將所有隨機單元的可靠度換算成用表示的形式,所有不確定單元的可靠度換算成用表示的形式,可得系統的確信可靠度為

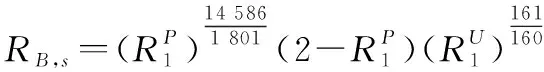
6.4 優化模型求解與分配結果輸出

對第63節的優化模型進行求解即可得各單元確信可靠度的最優分配方案,結果如表10所示。

表10 單元可靠度的分配結果

經驗算,此時系統的確信可靠度為0.8,恰好滿足指標要求。

7 結束語

本文以不確定隨機系統為研究對象,利用技術成熟度的相關信息,給出可行的確信可靠度分配方法。該方法充分考慮了可靠性評估時兩類不確定性的影響,獲得的分配方案既易于保證,又能降低成本,最后也通過實例證明了該分配方法的優良性。在未來的研究中,除技術成熟度和成本外,可以綜合考慮更多方面的影響因素,如工作環境狀況,從而實現系統確信可靠度更為合理的分配。