周期性低頻尾跡對邊界層演變影響的瞬態研究

孫海鷗， 任翱宇， 王艷華， 王忠義， 曲永磊

(哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001)

作為燃氣輪機的主要部件之一，壓氣機總是在強逆壓梯度條件下運行，這使得壓氣機葉片的運行環境惡劣。強逆壓梯度導致了更大的壓阻，加厚了葉片吸力面邊界層，從而導致更嚴重的邊界層分離和能量能量損失。

人們正詳細地研究和理解強逆壓梯度下的葉片表面流動機理。Pietro Zunino教授的團隊利用一個簡化的模型針對葉片表面的分離剪切層做了一系列的實驗研究。Bernardini等[1]用一個平板模型取代葉片，在平板的上下空間加裝內凹的擋板來制造逆壓梯度。當轉捩過程發生的時候，可以觀察到分離和再附著現象形成一個具備一定厚度的邊界層，稱為層流分離泡。Simoni等[2-3]對關于來流尾跡與層流分離泡不穩定機理之間的交互作用進行了實驗研究。將動葉尾緣簡化為擾流棒，極大降低了實驗的難度并使得關注重點落在尾跡對平板表面流動的影響上。該實驗在熱那亞大學的空氣動力與渦輪機械實驗室的一個開式低速風洞中進行，得到了關于大尺度渦結構的高清圖像[4]。以上這些帶有來流尾跡的研究工作得到了一些有意義的結論，比如粘性剪切層內速度波動得到了放大，且最大的波動會發生在分離邊界層最厚的位置附近；分離泡會表現出周期性的厚度變化，包含來流尾跡對分離泡的抑制作用。

鑒于發動機葉型的多樣性，針對平板進行研究易于得到表面流動分離的普適性的機理，但是目前通過對來流尾跡對平板表面分離流動影響的數值模擬來研究壓氣機葉片表面的邊界層演變做的較少。一些針對無擾流棒的平板數值模擬可以作為研究參考，除了上文提到的，還有李華君等[5]針對平板轉捩所做的詳細分析。通過LES模型計算，他們的文章認為分離剪切層內的轉捩過程是由流線型條紋和無粘Kelvin-Helmholtz不穩定性共同引起，前者占據了主要原因。該觀點與主流認為的Kelvin-Helmholtz不穩定性是引起轉捩的主要原因存在不同。張衡[6-7]對來流尾跡對渦輪葉片吸力面邊界層的影響進行了數值模擬研究，得到了大量關于來流尾跡和渦輪葉片吸力面邊界層厚度變化之間的定性分析。鄧飛等[8]利用振動降低近壁流場的湍流度，結果近壁處更加趨近于層流。

本文使用與文獻[1]中相同的物理模型作為研究對象，以方便數值方法的驗證。嘗試利用擾流棒與平板間的相互運動模式來代表壓氣機的級運動，聚焦于通過CFD方法揭示低頻尾跡對平板吸力面分離剪切層的周期性影響機理。該研究有利于加深對壓氣機葉片在強逆壓梯度下邊界層演變的理解，同時，對低頻尾跡與邊界層相互作用機理的關注同樣有助于為湍流運動機理分析提供可靠的參考。

1 數值方法與驗證

1.1 模型結構

用于數值模擬方法驗證的模型為圖1中擾流棒的右側部分，該未帶擾流棒的部分從參考文獻[1]提取，其關于平板表面邊界層分離的實驗研究在熱那亞大學空氣動力及渦輪機械實驗室完成。平板全長300 mm，包括有效弦長L=200 mm和尾緣100 mm，前緣為8∶1的橢圓形且平板厚度19.4 mm。平板被安裝在上下2塊擋板之間形成縮放通道來制造逆壓梯度環境。一個0.2 mm厚與1 mm寬的長方形薄片被粘貼在上端壁的喉道略靠后的位置，用來促進上部擋板表面的轉捩過程，從而減少甚至消除上部擋板表面的邊界層厚度對氣流通道壓力分布的影響。在數值模擬中直接設置上擋板表面壁面剪切力為0來起到相同作用。

圖1 模型結構圖及參數

在實驗中，平板內外兩側靠近測試段壁面處的數據精確度不高，因此采用圖3所示的平板縱向中截面來進行二維數值模擬。

1.2 數值模擬方法

在控制流動中，大尺度湍流和非穩定強迫擾動之間的相互作用是首要問題。為了獲得與大尺度渦旋相關的可靠結果，本文使用Fluent軟件中的壓力基URANS模型來預測全局流場。由ICEM軟件為模型提供完美的結構網格，包括30層極密的邊界層網格，來確保平板表面包括邊界層的厚度范圍內的Y+值遠遠小于1。通過在其余位置進行合理的網格布局，得到了高質量的全局網格。文獻[1]已經對2個不同的轉捩模型，transition SST 和transitionk-kL-ω進行了比較，結果表明transitionk-kL-ω模型在更多的測試區域貼合實驗結果，其預測性能優異。本文選擇該模型作為預測流動轉捩的數值模型，并基于the least squares cell進行空間離散，它在適用于多面網格方面與Green-gauss node-based 方法具有相同的精度。采用二階方案來進行壓力與動量的計算。

平板表面設置為無滑移壁面，上下擋板為滑移壁面，設置計算域壓力進口與靜壓出口，其中入口邊界條件湍流度為1.5%。對Re=70 000 和Re=200 000 這2種工況進行數值模擬。平板平直段長度L=200 mm為特征長度，由雷諾數換算得到質量流量作為流道壓力差的目標流量，并在靜壓出口條件中設置。

1.3 數值驗證

首先使用4套網格進行網格無關性的研究，使用平板上表面的平均表面摩擦系數Cf來評估收斂性能。圖2展示了網格計算的比較結果。在網格加密至數量超過64萬以后，平板表面的軸向Cf值幾乎不再變化，因此64萬這套網格為用作后續的數值模擬。

圖2 Re=70 000時不同網格對應的Cf 值

在Re=70 000和Re=200 000這2種條件下針對壓力系數Cp的CFD值與實驗值之間的校核如圖3所示。可以看出，數值模擬結果在絕大部分位置與實驗值相符合。在Re=70 000時數值模型的預測性能要優于Re=200 000的情況。因此，URAN計算和transitionk-kL-ω轉捩模型將作為本文后續數值研究的方法。

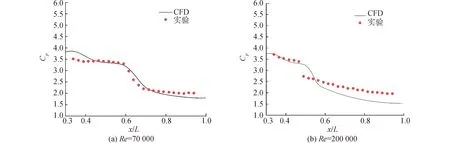
圖3 平板表面壓力系數分布

2 周期性來流條件設置

如圖2所示，在驗證模型的平板前端加入了垂直方向陣列布置的擾流棒。根據實驗，擾流棒圓心與平板前緣最前端之間的水平距離為66.67 mm，即1/3L。設定擾流棒向上運動，則平板的上表面代表壓氣機靜葉的吸力面。

擾流棒相關運動參數如下：折合頻率系數f+如式(1)所示，

(1)

是擾流棒頻率與軸向氣流流動頻率之間的比值，表征擾流棒運動與軸向氣流流動之間的交互關系。式中：Ubar是擾流棒移動速度，Sbar是擾流棒間距，c1原代表動葉出口氣流絕對速度，在平板流動研究中表示擾流棒區域前的軸向來流速度，Lchord是平板有效弦長200 mm。

速度比φ表示來流速度與擾流棒速度之間的相對關系，參考壓氣機中某級動葉轉速與出口氣流絕對速度，結合實驗經驗，選取φ值為2/3。

φ=c1/Ubar

(2)

鑒于在Re=70 000時的數值模擬結果具有更高的可靠性，選取該條件作為研究的來流參數，并據此確定來軸向來流速度c1。同時，設定f+=0.5，作為本文研究的低頻尾跡頻率。從而得到一系列邊界條件：環境溫度T=288.15K, 空氣密度ρ=1.225 kg/m3, 空氣動力粘度μ=1.789×10-5kg/(m·s), 進口軸向來流速度U0=4.992 m/s,Ubar= 7.488 m/s，擾流棒上移單周期為0.08 s，進口湍流強度為4%。擾流棒的向上平移通過網格移動來實現，擾流棒區域和前方來流區域，還有后方平板區域通過交界面連接。

自由流湍流度是流動分離的主要影響因素之一。Balzer等[9]的研究表明自由流湍流水平達到2.5%時在分離泡的上游出現流向條紋，轉捩同時由流向條紋和K-H不穩定性驅動。Simoni[10]在2.87%的湍流強度下進行研究時，發現層流泡會在雷諾數增加到90 000時消失。Zaki[11]對壓氣機葉片氣流分離的研究發現當自由流湍流度達到5.5%時，吸力面的分離完全消除，轉捩由針對T-S不穩定性的繞過機制主導。通常，低湍流度下的邊界層分離由K-H不穩定性主導，隨著湍流度的上升，K-H不穩定性的主導性下降。

由于湍流度隨著流體從邊界入口流向平板的過程中會略有降低，本文設置入口湍流度4%，計算得出平板前緣3個參考位置(如圖6所示)R1、R2、R3的平均湍流度分別約為3.35%、3.18%、3.07%。預計在該湍流度水平和70 000的入口雷諾數下層流分離泡不會消失。

3 結果與討論

3.1 平均流場分析

在計算中，單憑殘差線不足以作為收斂性的判斷，因此選擇流向的2個監測點(x/L=0.5和x/L=1, 高于平板平板上表面2 mm)來輔助判斷收斂性。最終，除去計算中尚未收斂的起始階段與可靠性較差的末尾階段，選取穩定性較好且時間連續的若干周期用于結果分析。通過雷諾平均得到穩定來流條件下的邊界層分離狀態如圖4所示，并在表1中提供穩定來流與周期性來流條件的部分邊界層數據。

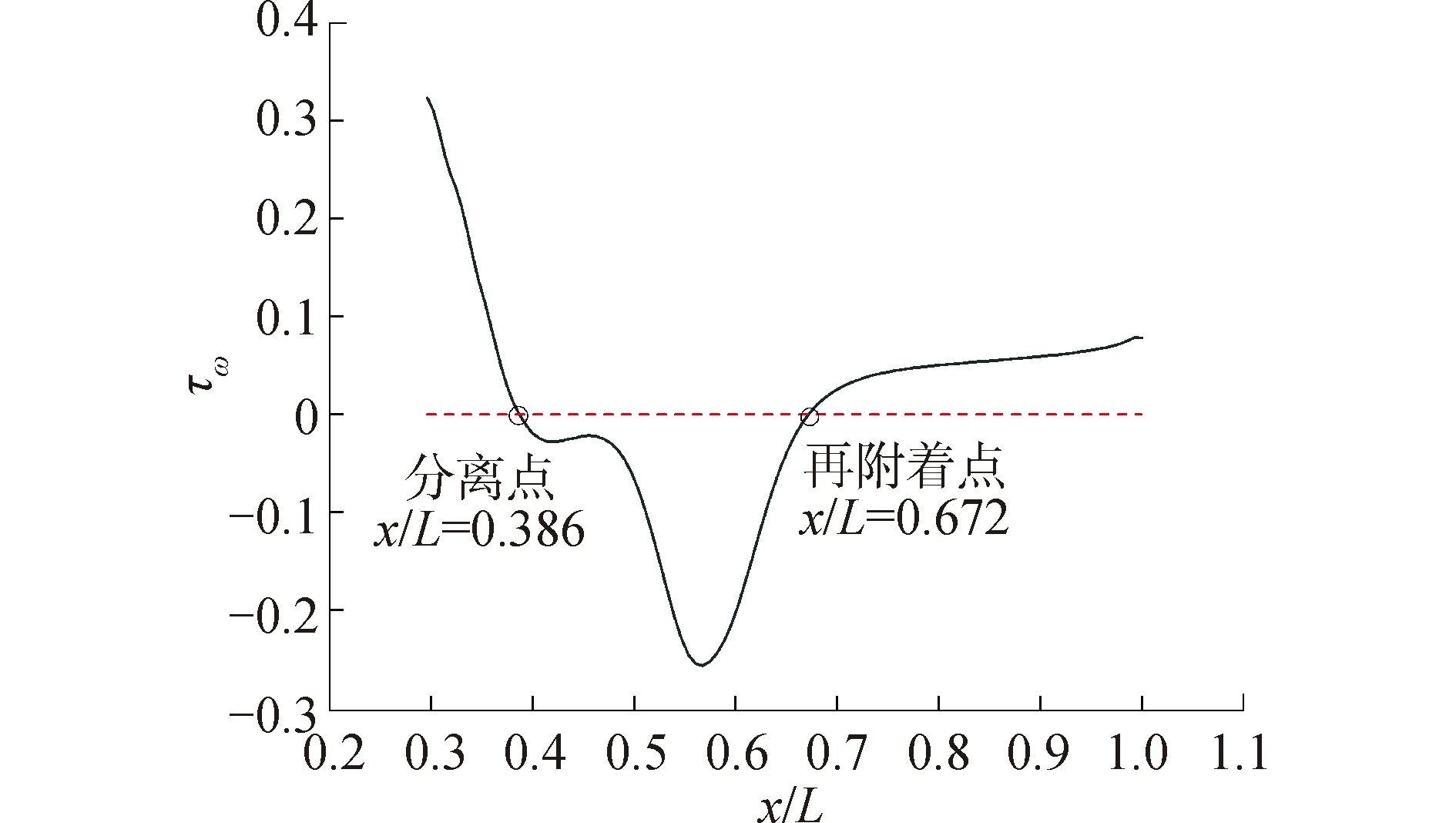
圖4 穩定來流狀態下壁面流向剪切力分布

表1 2種來流條件下分離區參數對比

穩定來流狀態的平均分離點在x/L=0.386左右，f+=0.5的周期性來流條件下平均分離點為x/L=0.382，略提前于穩定來流條件。文獻[3]中設置了f+=0.8的周期性來流條件，其實驗結果顯示平均分離點同樣略提前于穩定來流條件。

選擇平板表面相距較寬的3個點來計算其速度型線，以查看周期性來流下平板表面發生的流動狀態變化，如圖5所示。x/L=0.3處的速度型線是典型的牛頓流體層流狀態，x/L=0.55處的負向速度型線表征了該區域的流動分離，在平板末端x/L=1處的速度型線則表示了湍流狀態。該圖表明了周期性來流條件下平板表面的層湍轉捩的存在。

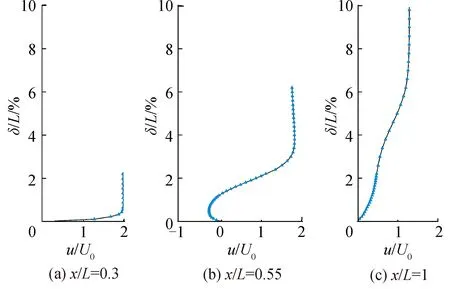
圖5 周期性來流頻率f+=0.5時平板表面3點處速度型線

基于圖5估算邊界層厚度，設置從點A(x/L=0.3,y/L=0.06)到點B(x/L=1,y/L=0.06)的數據采集線AB線。與x軸平行的AB line將被用于研究速度分布。本文確保該數據采集線穿越近壁的速度震蕩區并且有足夠的流體填充周圍區域。如圖6所示。

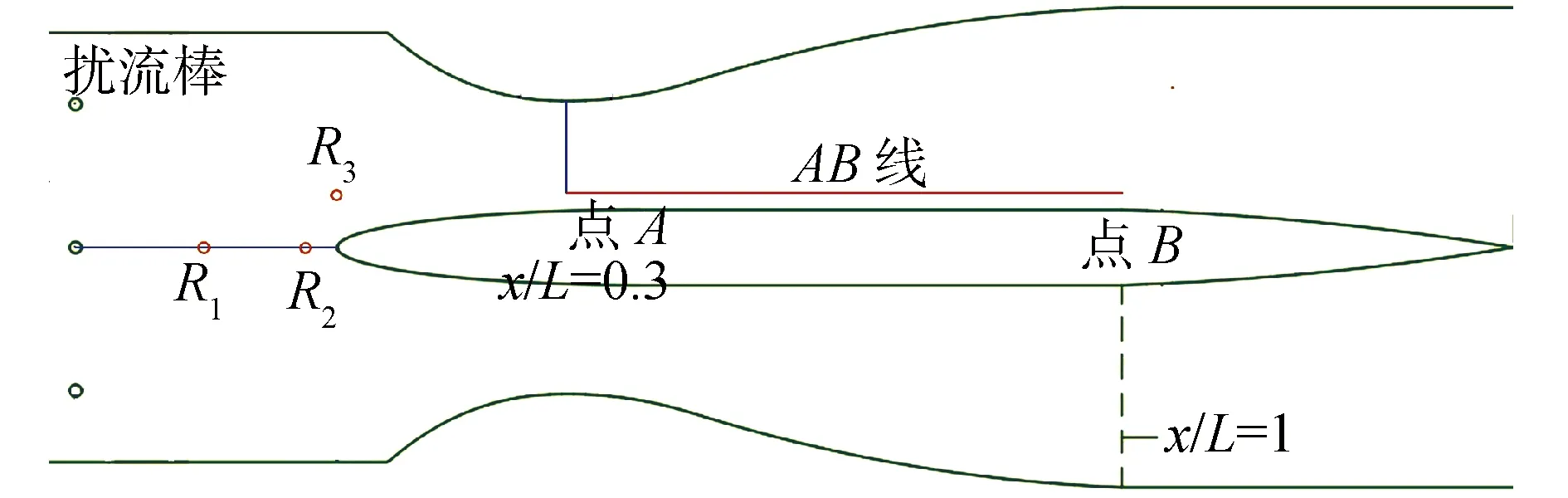
圖6 數據點采集點示意

圖7采用雷諾平均方法展示了流向與法向2個速度量在穩定來流與周期性來流條件下沿數據采集線AB線的分布。顯然，從全局平均統計來看，低頻來流尾跡的周期性作用沒有改變平板表面邊界層的基本運動趨勢，但是導致了局部的流動能量的加強與減弱。對于2種來流條件來說，流向速度最小值區域都位于約x/L=0.55的位置；而對于法向速度最小值，相比于穩定來流條件，周期性來流條件下該區域略向后延遲。

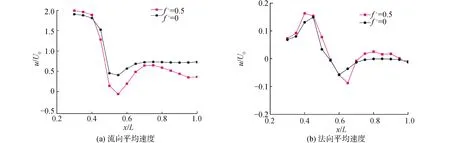
圖7 ABline對應的平均速度分布

3.2 分離剪切層運動分析

圖8和圖9中的渦量云圖提供了關于尾跡如何影響邊界層演變的清晰過程。擾流棒拖出了一條明顯的馮卡門渦街(V-K渦)。圖8的各個時刻中，尾跡尚未對邊界層產生影響，此時平板表面邊界層的內在演變起主要作用。氣流在接近x/L=0.4的位置開始分離，以流向條紋的形式，即圖中A1區域前的長條結構，到達邊界層最高處，并在末端形成大渦。分離剪切層內首先在A1區形成大渦，A1渦沿流向前進至A2區，A2區大渦順流進入A3區。從t/T=0.05可以發現A1渦的前面壁面處，A1與A2渦之間的壁面處，均有渦尖突起，標記為B1，B2。A渦均為順時針旋轉方向，與此相反的，B系列渦尖為逆時針旋向，但在A1渦的擠壓與A2渦的誘導下，B2區渦尖被向上擠壓拉伸，成為A2渦的半渦環，并在A2渦進入A3區后成為其全渦環。如t/T=0.075所示，流向條紋末端不斷產生新的旋渦，放大，脫落，沿流向推進，伴隨B區渦尖環繞脫落的渦沿平板表面上部一定距離的位置流向推進，并伴隨能量衰減，該過程周而復始。這一演變過程明顯的證明了以大渦為特征的K-H不穩定性的存在。

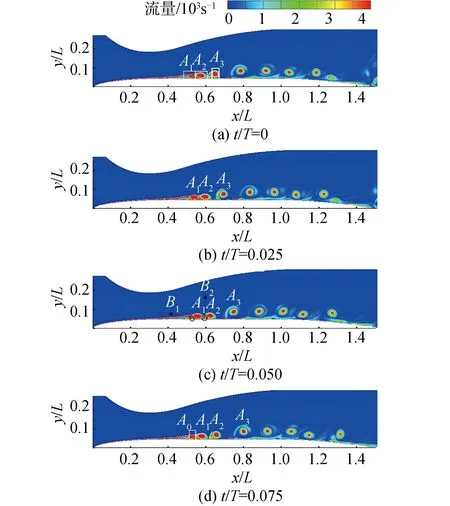
圖8 尾跡作用之前分離剪切層內渦量狀態云圖

周期性尾跡與平板表面分離剪切層交互作用的過程如圖9所示。t/T=0.3是尾跡接觸分離區的起點，以t/T=0.425尾跡對分離區最后的影響為結束。通過放大視角觀察圖10中對分離區交互作用狀態，發現在t/T=0.3尾跡接觸初始分離區的流向條紋時，尾跡中的V-K渦將流向條紋初始段中的部分能量誘導出原有路徑并跟隨V-K渦前進。通過觀察t/T=0.3與t/T=0.35，有理由認為該V-K渦的誘導過程持續了整個流向條紋階段。在尾跡渦進入分離核心區后，即t/T=0.35，尾跡壓制了下方的渦使分離剪切層變窄，同時既拉伸了后方的渦，也強化了B2渦尖，帶動尾跡后方的渦伴隨迅速強化的渦尖脫離平板表面沿流向運動。由于尾跡對分離區的壓迫，條紋末端初始渦短暫地改變了形態，如圖10中t/T=0.375所示，但在t/T=0.4時迅速恢復，然而尾跡的前進速度明顯高于分離區渦的內在脫落速度，導致了流向條紋末端新生渦的成型過程被壓制，緊鄰的成型渦被尾跡迅速帶走，兩渦之間的間距被拉大，該過程周期性變化，使得分離區的實際長度，包括再附著點，也呈現周期性的變化。即使尾跡已經掠過分離區，其動量輸入卻未結束，表現在t/T=0.425中流向條紋末端本應形成初始渦的區域被拉長成扁平狀。在此之后，尾跡對分離區影響消失。尾跡對分離核心區的持續影響時間約為0.125個周期。

圖9 尾跡與分離剪切層的交互作用

圖10 分離區交互作用放大示意

尾跡對分離區的壓制作用導致了反向作用力，使其本身形態發生改變。t/T=0.4時刻尾跡V-K渦與分離區固有脫落渦存在明顯摻混狀態。平板表面分離剪切層的存在進一步減少了喉部以后的通道截面積，加快了尾跡的前進速度，因此我們看到在尾跡離開分離區后的t/T=0.45至t/T=0.525階段，圖中區域C至E，尾跡通過一種順時針的卷吸作用對從分離區內率先帶出的渦進行了加速與順時針旋轉，使其高于并趕上臨近的后部渦，繼而導致雙渦摻混旋轉前進。后部渦被卷吸至下方，導致緊鄰的下一個渦更易受到尾跡卷吸，重復作用，得到了圖中所示的尾跡離開分離區后對平板表面脫落渦的成對卷吸摻混現象。該作用加快了分離轉捩區后部高能渦的能量耗散，加強了湍流的均勻性。

3.3 轉捩分析

利用FFT(快速傅里葉轉換)來采集AB line上的二維速度信息，得到關于速度波動能量譜密度圖11所示。

平板的前端x/L=0.3處未見明顯波峰。實際上x/L=0.3之前為順壓區，本身不太可能出現T-S波。x/L=0.3之后為逆壓區，若此時存在T-S波則應在平均分離點x/L=0.382之前出現明顯的波峰，但即使到x/L=0.45處，依然沒有明顯的波峰。文獻[5]的研究顯示在平板前緣湍流度2.9%的狀態下T-S不穩定性階段被繞過了。由于本文平板前緣的湍流度略高于該數值，有更大概率繞過T-S不穩定性。該文獻同時認為流向條紋的出現是T-S波被繞過的征兆之一。從x/L=0.5開始30 Hz段的低頻能量顯著增強，高頻波峰逐漸趨顯，說明分離過程趨于嚴重并伴隨內部渦的產生。從流向平均速度曲線來看，x/L=0.55附近應為分離剪切層最大厚度的位置，從PSD曲線看，此時低頻波峰最為明顯并伴隨微弱的高頻波峰，表明該位置的邊界層分離最為劇烈并占據主導地位，同時伴隨一定程度的渦運動。x/L=0.65處出現最為明顯的180～200 Hz高頻能量波峰，低頻波峰消失，該區域附近為渦的脫落擴散最為激烈的區域，表明K-H不穩定性占據轉捩過程的主導地位[12-13]。

圖11中說明的分離層內能量的能量分布同樣在圖12中的AB線平均速度波動曲線得到證明。在全局平均尺度下，層流分離泡的上游速度波動能量維持了穩定狀態，分離開始后其分離區內部擾動能量迅速上升，至x/L=0.55與x/L=0.65區間高頻能量明顯顯現，如圖11中對應階段波峰的出現。流過高頻振蕩區后，隨著再附著過程和轉捩后湍流的擴散，速度振蕩能量趨于下降。

圖11 周期性來流f+=0.5條件下邊界層的PSD分析

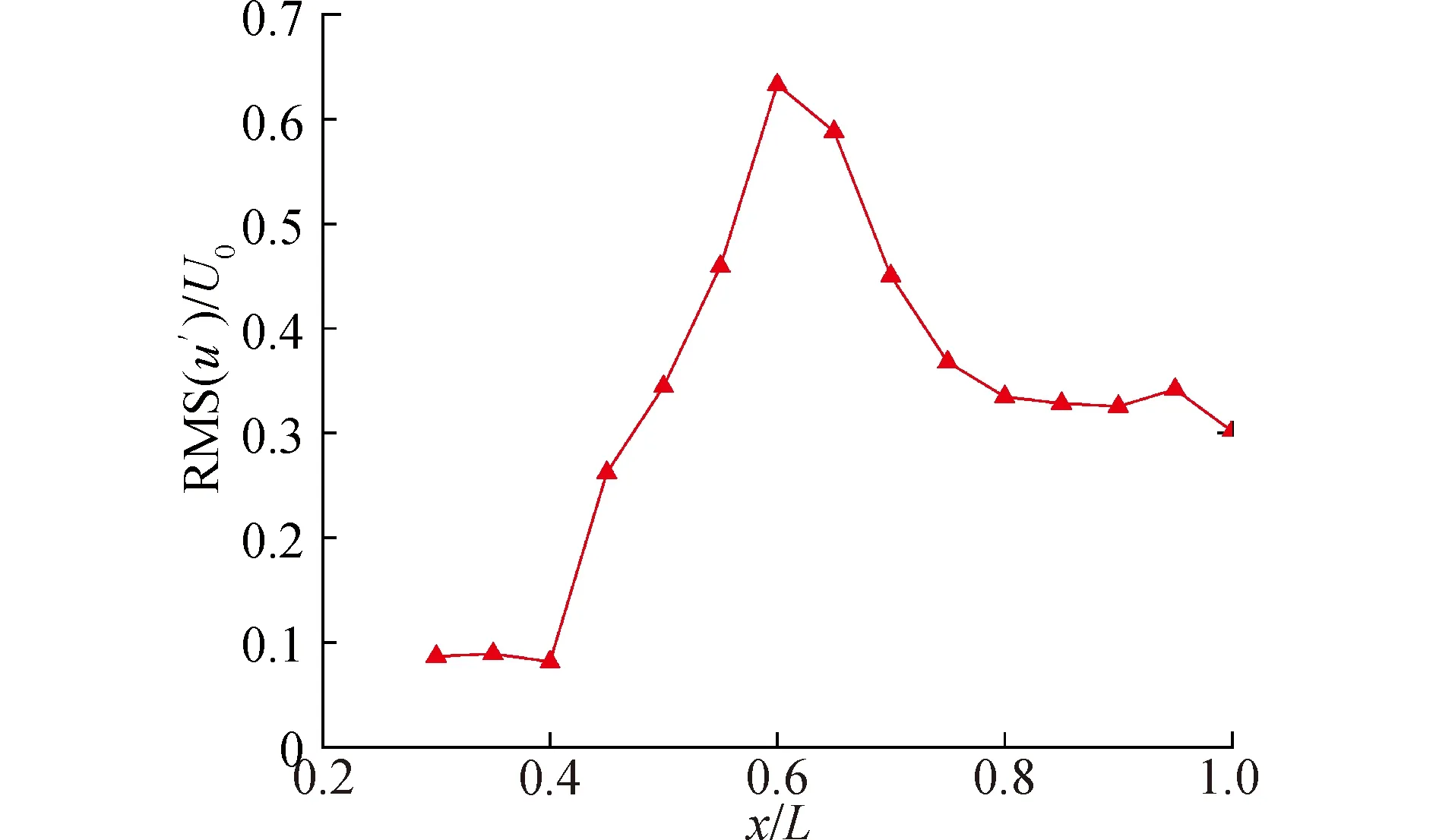
圖12 ABline 均方根速度波動分布

在時間與空間的共同尺度下對速度波動能量進行分析，有助于理解分離剪切層在尾跡影響下的演變機理[14-15]。以t/T=0.3時刻尾跡與分離泡前緣接觸時為起始時刻，此時的平板表面流線狀態如圖13所示。在分離轉捩區內貼近分離剪切層上層區域沿t/T=0.3時刻尾跡前進方向取9個數據點，計算其速度波動能量變化，如圖14所示。

圖13 t/T=0.3時刻平板表面速度流線

速度波動的均方根值為圖14所示，t/T=0.3時刻的能量沿著時間在分離層內流向推進。隨著上游能量的推進與作用，層流分離階段內速度波動呈現線性上升趨勢，并在大約分離區最厚處達到最大。這一過程印證了線性不穩定性的存在。由于尾跡誘導的低頻能量被引入分離剪切層后被逐步放大至高頻能量，速度振蕩能量呈指數上升趨勢，如圖14所示，這與文獻[3]的實驗分析結果一致。速度波動能量在經過x/L=0.6～0.65區間后趨向下降，表明這一區間能量振蕩的放大達到飽和狀態，并誘導轉捩，導致下游能量振蕩水平的下降。

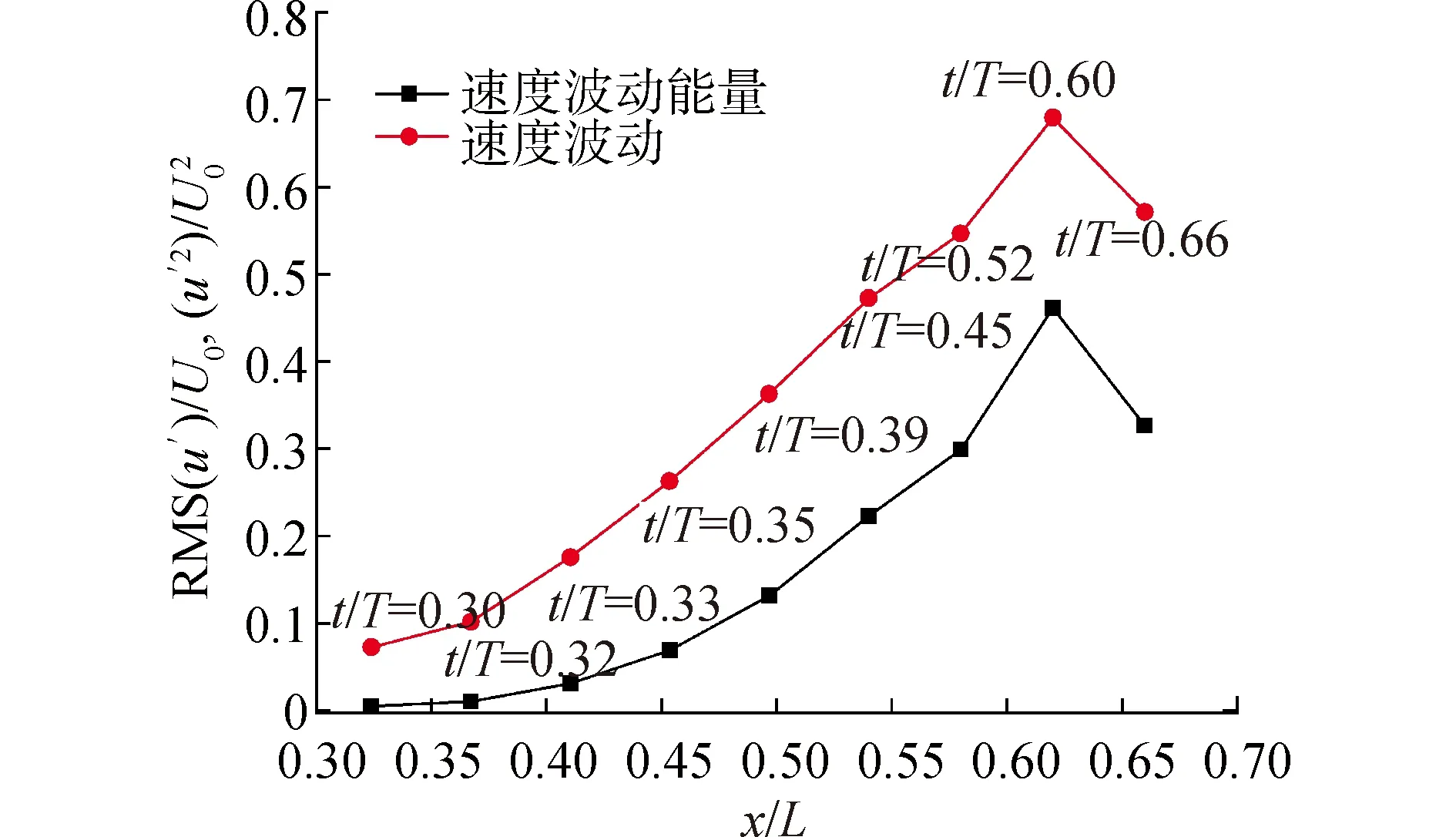
圖14 分離轉捩區受t/T=0.3尾跡作用的時間-空間能量變化曲線

4 結論

1)相比于無尾跡的穩定來流狀態，周期性尾跡來流條件略微提前了平板表面的氣流分離點，再附著點由于尾跡的帶動卷吸作用呈現多點周期性后移現象，難以有相對確定位置。

2)分離核心區渦的演變模式為核心渦與間隙渦發展的渦環成對出現，該固有模式受到來流尾跡的促進。

3)尾跡對分離泡的抑制作用表現為尾跡對分離區能量輸出使得層流泡內本應形成的初始渦被壓縮拉長，但并非貫穿全程，而是呈現周期性特性，在尾跡掠過分離區時產生，約為0.125個擾流棒周期。

4)在平板前緣3%左右的湍流度與f+=0.5的低頻尾跡來流條件下，其轉捩機理如下：分離轉捩區內高能震蕩區在x/L=0.65左右，約為180～200 Hz。進入分離剪切層的低頻能量在線性不穩定性的作用下指數型放大為高頻能量，最終誘導分離區轉捩。流向條紋，K-H不穩定性和尾跡振蕩能量的輸入共同導致了邊界層的轉捩，未發現明顯的T-S不穩定性。

然而，在穩定來流條件下，足夠高的湍流度(>5%)可以導致分離泡消失，但是在具有來流尾跡時，多大的來流湍流度可以導致K-H不穩定性被繞過，則是值得繼續研究的問題。