一種基于參數(shù)控制的低軌星載接收機(jī)載波跟蹤算法

檀曉萌, 羅瑞丹, 徐 穎, 蘇 中, 袁 超

(1.北京信息科技大學(xué)自動(dòng)化學(xué)院高動(dòng)態(tài)導(dǎo)航技術(shù)北京市重點(diǎn)實(shí)驗(yàn)室，北京 100101；2.中國(guó)科學(xué)院空天信息創(chuàng)新研究院，北京 100094)

0 引言

隨著衛(wèi)星導(dǎo)航系統(tǒng)(Global Navigation Satelli-te System，GNSS)的現(xiàn)代化升級(jí)與組網(wǎng)完善，星載自主導(dǎo)航接收機(jī)作為空間航天器必備載荷，能夠?yàn)楹教炱魈峁└呔取⒏呖捎谩?shí)時(shí)連續(xù)的定軌、測(cè)姿、授時(shí)等信息，極大地提高了航天器運(yùn)行自主性，對(duì)于保障航天任務(wù)具有十分重要的意義。

低軌(Low Earth Orbit，LEO)衛(wèi)星因其特有的平臺(tái)優(yōu)勢(shì)，成為支撐大氣探測(cè)、海洋測(cè)高、重力場(chǎng)模型精化等科學(xué)探測(cè)任務(wù)的重要平臺(tái)，對(duì)應(yīng)LEO星載導(dǎo)航接收機(jī)研制也成為未來(lái)導(dǎo)航研究與低軌定軌的重要研究方向。同時(shí)，LEO衛(wèi)星因其軌道和任務(wù)特性，使得其建設(shè)向著平臺(tái)體積集約化、星座規(guī)模巨型化、功能任務(wù)復(fù)合化、業(yè)務(wù)服務(wù)精細(xì)化等方向發(fā)展，這也要求LEO星載接收機(jī)在低功耗、高精度等方面具備明顯的性能優(yōu)勢(shì)。

但是LEO衛(wèi)星運(yùn)行速度可達(dá)每秒數(shù)千米，為星載接收機(jī)引入大多普勒頻移與頻繁快速換星等設(shè)計(jì)難題。特別地，對(duì)接收機(jī)載波跟蹤環(huán)路提出了較高的動(dòng)態(tài)適應(yīng)性和跟蹤精度要求，同時(shí)基于星上資源和實(shí)現(xiàn)復(fù)雜度考慮，載波跟蹤環(huán)路設(shè)計(jì)也不宜過(guò)度復(fù)雜。

目前，國(guó)內(nèi)外針對(duì)LEO星載接收機(jī)跟蹤環(huán)路的設(shè)計(jì)算法，從原理上可以分為三大類：1)基于經(jīng)典環(huán)路輔助/組合的載波環(huán)，如鎖頻環(huán)(Frequency-Locked Loop，F(xiàn)LL)輔助鎖相環(huán)(Phase-Locked Loop，PLL)。FLL輔助PLL結(jié)構(gòu)中通過(guò)FLL和PLL之間的切換，用FLL進(jìn)行大頻偏的輔助捕捉，PLL進(jìn)行精確跟蹤，其結(jié)構(gòu)較為簡(jiǎn)單，但環(huán)路參數(shù)的確定比較困難，在星載環(huán)境下，切換機(jī)制導(dǎo)致的環(huán)路穩(wěn)定性下降更為明顯。2)基于慣導(dǎo)輔助的載波環(huán)，通過(guò)速率輔助去掉大部分動(dòng)態(tài)，實(shí)現(xiàn)高精度跟蹤，但慣導(dǎo)系統(tǒng)造價(jià)高昂、結(jié)構(gòu)復(fù)雜，導(dǎo)致其在星載環(huán)境下應(yīng)用受限。3)基于參數(shù)估計(jì)理論的載波環(huán)，如最大似然估計(jì)載波環(huán)、卡爾曼濾波/擴(kuò)展卡爾曼濾波/無(wú)跡卡爾曼濾波載波環(huán)、粒子濾波/無(wú)跡粒子濾波載波環(huán)等。這類算法將信號(hào)過(guò)程看作系統(tǒng)輸入白噪聲的過(guò)程，自適應(yīng)地調(diào)整環(huán)路參數(shù)，但只適應(yīng)于特定的系統(tǒng)，算法魯棒性較差，且運(yùn)算量較高，不易于在資源受限的星載接收機(jī)上進(jìn)行工程實(shí)現(xiàn)。

針對(duì)低軌星載接收機(jī)引入大多普勒頻移問(wèn)題及頻繁快速換星需求，傳統(tǒng)載波跟蹤算法(鎖相環(huán))無(wú)法兼顧跟蹤精度與收斂速度，因此，本文提出了一種基于參數(shù)控制的載波跟蹤環(huán)路(Parameter Control Factor Phase-Locked Loop，PCF-PLL)。該環(huán)路將環(huán)路濾波器分為牽引濾波器和跟蹤濾波器兩種狀態(tài)，通過(guò)參數(shù)控制因子實(shí)現(xiàn)兩濾波器的協(xié)同配合，有效地解決了大多普勒頻移問(wèn)題，實(shí)現(xiàn)了環(huán)路快速入鎖，提高了環(huán)路跟蹤精度和魯棒性；同時(shí)將更多的多普勒頻移引入載波跟蹤環(huán)處理，可降低捕獲環(huán)節(jié)的計(jì)算量和復(fù)雜度，提高星載接收機(jī)整體的工作效率，環(huán)路設(shè)計(jì)簡(jiǎn)單，有利于硬件實(shí)現(xiàn)。

1 GNSS-LEO信號(hào)多普勒特性分析

GNSS-LEO信號(hào)為基于LEO星載平臺(tái)觀測(cè)接收到的GNSS信號(hào)，其信號(hào)多普勒頻移是由GNSS衛(wèi)星與LEO衛(wèi)星之間的相對(duì)運(yùn)動(dòng)引起的，LEO衛(wèi)星速度、GNSS衛(wèi)星速度在GNSS-LEO直線距離上的投影之和直接影響信號(hào)多普勒頻移大小，LEO衛(wèi)星與GNSS衛(wèi)星的位置如圖1所示。

圖1 LEO與GNSS衛(wèi)星相對(duì)位置示意圖Fig.1 The relative position of LEO and GNSS

多普勒頻移可表示為

(1)

式中

(2)

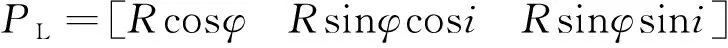
(3)

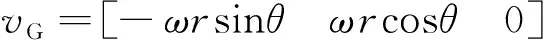
(4)

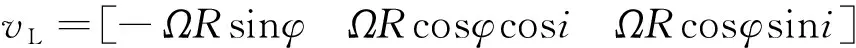
(5)

式中：為GNSS-LEO信號(hào)多普勒頻移；為GNSS-LEO信號(hào)載波頻率；為光速；、為GNSS、LEO衛(wèi)星的位置；、為GNSS、LEO衛(wèi)星的速度；、為L(zhǎng)EO、GNSS的軌道半徑；、為L(zhǎng)EO、GNSS的角速度；為GNSS軌道與LEO軌道之間的傾角；為L(zhǎng)EO衛(wèi)星位置與軸夾角；為GNSS衛(wèi)星位置與軸夾角。

由上述公式可知，GNSS-LEO信號(hào)多普勒特性與衛(wèi)星的位置、速度等運(yùn)動(dòng)狀態(tài)密切相關(guān)，兩衛(wèi)星速度在兩者直線距離方向上的投影和越大，多普勒頻移越大。衛(wèi)星的運(yùn)動(dòng)狀態(tài)直接與其軌道高度有關(guān)，目前低軌衛(wèi)星的軌道高度一般為120～2000km，故本文選取LEO軌道高度為500km，基于STK進(jìn)行仿真，得到GNSS-LEO信號(hào)多普勒頻移及其相關(guān)特性如表1所示。

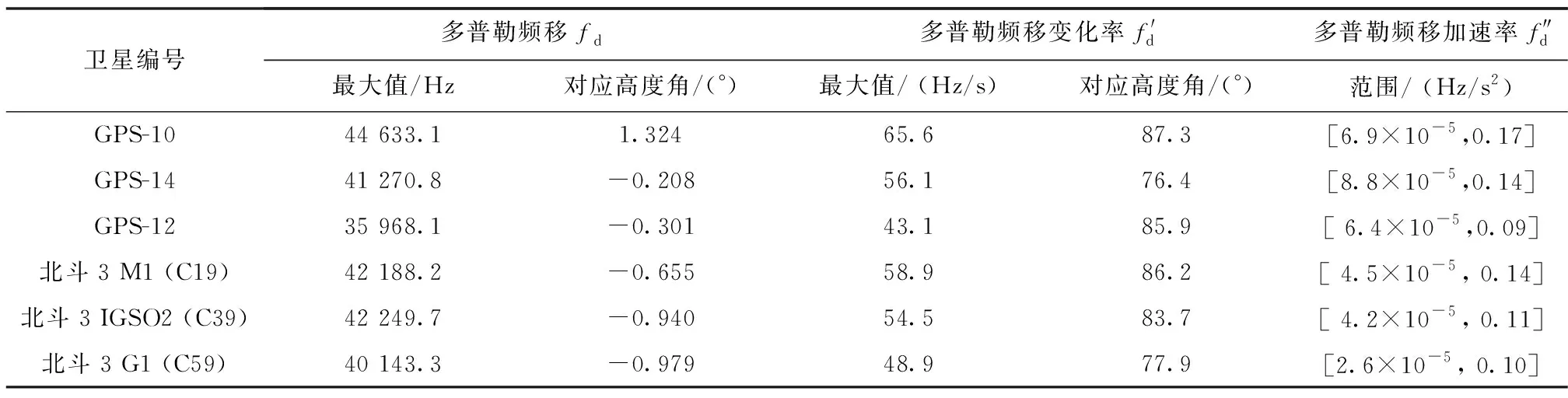
表1 GNSS-LEO信號(hào)的多普勒頻移參數(shù)

由表1可得，GNSS-LEO信號(hào)載波多普勒頻移最大值為45kHz左右，多普勒頻移變化率最大值不超過(guò)70Hz/s，多普勒加速率范圍為[0Hz/s～0.2Hz/s]。所有GNSS-LEO信號(hào)數(shù)據(jù)的最大多普勒頻移對(duì)應(yīng)的高度角都較低，在0°左右，即最大多普勒頻移發(fā)生在GNSS-LEO之間剛可見或即將不見的時(shí)刻；而最大多普勒頻移變化率對(duì)應(yīng)的高度角多數(shù)偏高，主要是因?yàn)樽畲蠖嗥绽疹l移變化率發(fā)生在GNSS衛(wèi)星過(guò)頂LEO衛(wèi)星時(shí)刻。

選取LEO-GPS01信號(hào)最大多普勒頻移最大的一組數(shù)據(jù)作為接收機(jī)載波跟蹤環(huán)路的輸入信號(hào)，其載波多普勒、多普勒頻移變化率及多普勒加速率如圖2所示,載波多普勒、多普勒頻移變化率與GPS高度角如圖3所示。

由圖2可得，LEO-GPS01信號(hào)載波多普勒頻移可達(dá)40kHz，載波多普勒變化率最大不超過(guò)60Hz/s，載波多普勒加速率范圍為[0Hz/s～0.15Hz/s]，基本可視為0。由圖3可得，LEO-GPS01信號(hào)最大多普勒頻移發(fā)生時(shí)，對(duì)應(yīng)GPS高度角在-5°～-10°之間；而最大多普勒頻移變化率對(duì)應(yīng)的GPS高度角為45°左右。

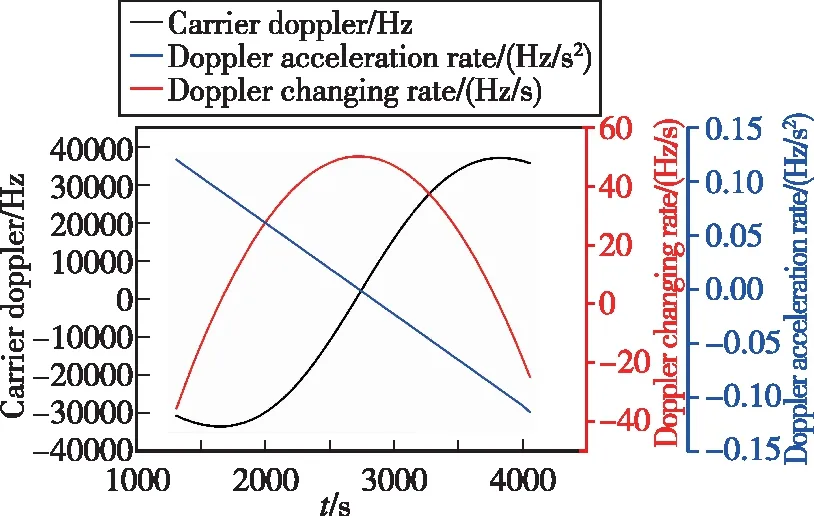
圖2 LEO-GPS01載波多普勒信息圖Fig.2 Carrier Doppler of LEO-GPS01 signal

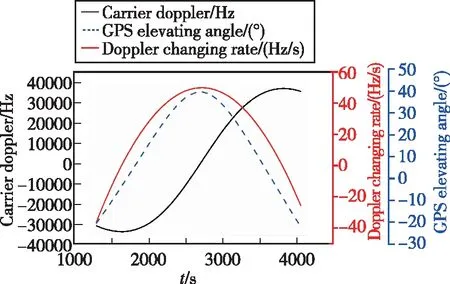
圖3 LEO-GPS01載波多普勒信息與高度角Fig.3 Carrier Doppler and GPS altitude angle of LEO-GPS01 signal

由表1可知，低軌星載接收機(jī)的高動(dòng)態(tài)環(huán)境主要表現(xiàn)為大的多普勒頻移、不高的多普勒頻移變化率和可忽略不計(jì)的多普勒加速率。同時(shí)，GNSS-LEO可見持續(xù)時(shí)間較短，平均為47min左右，且為保證精細(xì)觀測(cè)，需要頻繁換星，這對(duì)星上接收機(jī)的處理速度及跟蹤精度要求更高。

2 PCF-PLL

針對(duì)在GNSS-LEO信號(hào)跟蹤中引入大多普勒頻移導(dǎo)致入鎖慢、接收機(jī)處理難度及復(fù)雜度較大的問(wèn)題，本文提出了一種PCF-PLL。該環(huán)路將環(huán)路濾波器狀態(tài)分為牽引和跟蹤兩階段，引入?yún)?shù)控制因子調(diào)整濾波器狀態(tài)，從而達(dá)到快速入鎖、精確穩(wěn)定跟蹤且不增加環(huán)路復(fù)雜度的目的。

2.1 PCF-PLL算法原理

為使接收機(jī)在動(dòng)態(tài)環(huán)境下具有較高的魯棒性，最有效的方法之一就是增加環(huán)路帶寬。PCF-PLL算法基于此，將環(huán)路濾波器分為兩種狀態(tài)：1)牽引濾波器，主要實(shí)現(xiàn)牽引信號(hào)快速入鎖的功能；2)跟蹤濾波器，主要實(shí)現(xiàn)精確跟蹤信號(hào)的功能。為降低環(huán)路參數(shù)設(shè)計(jì)復(fù)雜度，通過(guò)參數(shù)控制因子實(shí)現(xiàn)牽引濾波器和跟蹤濾波器的協(xié)同工作，簡(jiǎn)單易行地完成接收機(jī)高動(dòng)態(tài)穩(wěn)定跟蹤。PCF-PLL算法原理如圖4所示，圖4(a)為PCF-PLL環(huán)路框圖，圖4(b)為PCF-PLL牽引濾波器框圖，圖4(c)為PCF-PLL跟蹤濾波器框圖。

如圖4(a)所示，PCF-PLL的傳遞函數(shù)表達(dá)式為

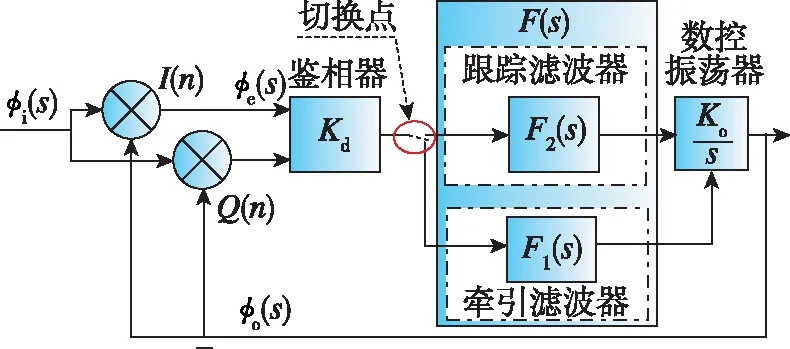
(a) PCF-PLL環(huán)路框圖

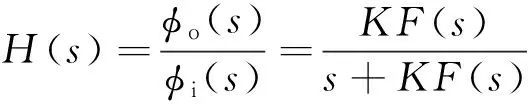
(6)

式中：()為環(huán)路濾波器傳遞函數(shù)；為環(huán)路增益，表達(dá)式為

=

(7)

式中：、分別為鑒相器和數(shù)控振蕩器的增益。

從而可得PCF-PLL的誤差傳遞函數(shù)表達(dá)式為

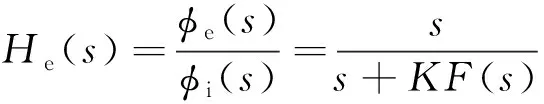
(8)

如圖4(b)所示，PCF-PLL牽引濾波器的傳遞函數(shù)可表述為

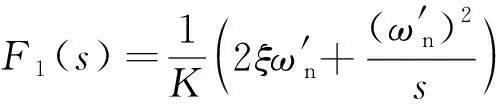
(9)

式中：為阻尼系數(shù)；為參數(shù)控制因子；′為牽引階段環(huán)路的特征頻率。

將式(9)代入式(6)和式(8)可得PCF-PLL牽引階段傳遞函數(shù)及誤差傳遞函數(shù)為

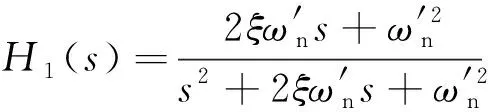
(10)

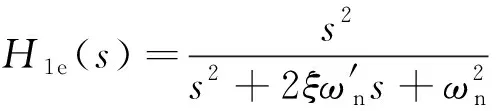
(11)

同理，如圖4(c)所示，PCF-PLL跟蹤濾波器的傳遞函數(shù)、跟蹤階段傳遞函數(shù)及誤差傳遞函數(shù)分別為

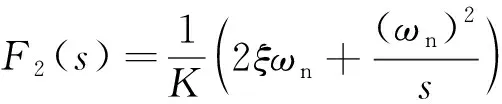
(12)

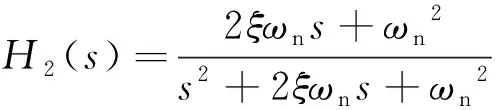
(13)

(14)

為簡(jiǎn)化PCF-PLL分析，對(duì)兩階段的傳遞函數(shù)和誤差函數(shù)進(jìn)行規(guī)范化，引入一個(gè)參數(shù)控制因子，其表達(dá)式為

′=

(15)

由式(15)可得，參數(shù)控制因子可建立牽引濾波器和跟蹤濾波器之間的關(guān)系，使2個(gè)獨(dú)立的濾波器參數(shù)實(shí)現(xiàn)協(xié)同調(diào)整，降低環(huán)路復(fù)雜度。當(dāng)參數(shù)控制因子≤1時(shí)，誤差傳遞函數(shù)值減小，環(huán)路濾波器即跟蹤濾波器,對(duì)應(yīng)環(huán)路跟蹤階段；反之，為牽引濾波器，對(duì)應(yīng)環(huán)路牽引階段。

則PCF-PLL環(huán)路傳遞函數(shù)及誤差傳遞函數(shù)為

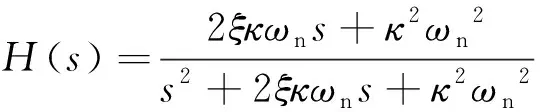
(16)

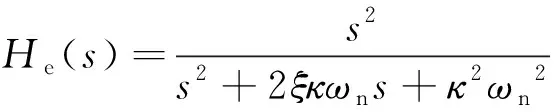
(17)

根據(jù)式(13)可推導(dǎo)PCF-PLL環(huán)路帶寬公式為

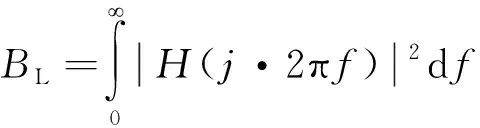
(18)

由式(18)可知，環(huán)路帶寬與參數(shù)控制因子成正比。故可通過(guò)調(diào)整參數(shù)控制因子，調(diào)整接收機(jī)靈敏度及測(cè)距精度。

為保證環(huán)路整體計(jì)算量較小，本文采用計(jì)算量更小的鑒相器，其表達(dá)式為

()=

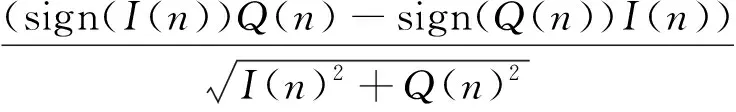
(19)

式中：()和()分別為時(shí)刻同相支路和正交支路的相關(guān)輸出結(jié)果；sign(·)為符號(hào)函數(shù)。

由圖4(a)可得，鑒相器與環(huán)路濾波器之間存在一個(gè)切換點(diǎn)，用來(lái)切換環(huán)路濾波器的狀態(tài)，從而控制整個(gè)環(huán)路的狀態(tài)。當(dāng)接收機(jī)首次啟動(dòng)或出現(xiàn)GPS信號(hào)丟失、失鎖時(shí)，載波跟蹤環(huán)路首先進(jìn)入PCF-PLL牽引階段，通過(guò)牽引濾波器的牽引作用快速縮小信號(hào)頻差范圍，實(shí)現(xiàn)快速入鎖、持續(xù)穩(wěn)定跟蹤；當(dāng)信號(hào)頻差范圍縮小至PLL可跟蹤時(shí)，環(huán)路濾波器切換為跟蹤濾波器，實(shí)現(xiàn)精確跟蹤。

通過(guò)上述分析可得，PCF-PLL引入的參數(shù)控制因子不僅實(shí)現(xiàn)了牽引濾波器與跟蹤濾波器的協(xié)同配合，且與環(huán)路帶寬直接相關(guān)，可通過(guò)調(diào)整接收機(jī)靈敏度及跟蹤精度，提高PCF-PLL在高動(dòng)態(tài)環(huán)境下的魯棒性。此外，PCF-PLL還采用了計(jì)算量更小的鑒相器，使得整個(gè)環(huán)路的計(jì)算量及復(fù)雜度與PLL相當(dāng)。

2.2 PCF-PLL性能推導(dǎo)

本文基于PCF-PLL算法原理，推導(dǎo)了參數(shù)控制因子與環(huán)路的收斂速度及跟蹤誤差之間的表達(dá)式，給PCF-PLL參數(shù)優(yōu)化提供了理論依據(jù)。

2.2.1 PCF-PLL收斂速度

接收機(jī)的收斂速度一般定義為環(huán)路起始的誤差響應(yīng)幅值衰減至其1/4所需的時(shí)間，用收斂時(shí)間來(lái)表示。通過(guò)推導(dǎo)環(huán)路誤差響應(yīng)幅值公式，可得收斂時(shí)間的表達(dá)式。

環(huán)路誤差響應(yīng)幅值與輸入信號(hào)的類型有關(guān)。當(dāng)輸入信號(hào)()包含相位階躍信號(hào)、頻率階躍信號(hào)及頻率斜升信號(hào)時(shí)，如下

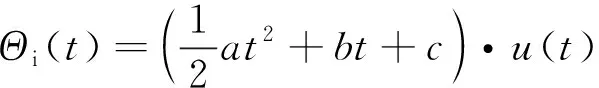
(20)

式中：為頻率斜升值；為頻率階躍值；為相位階躍值；()為單位階躍序列。

此時(shí)，PCF-PLL誤差響應(yīng)()為

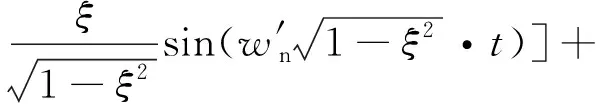
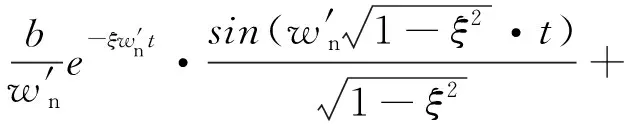
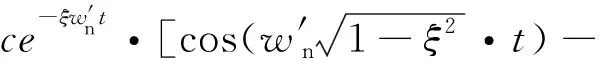
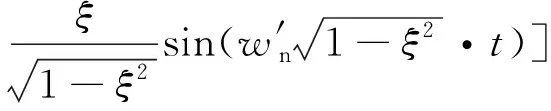
(21)

可得收斂時(shí)間的表達(dá)式為

(22)

由式(22)可得，環(huán)路的收斂時(shí)間與參數(shù)控制因子成反比。通過(guò)增大參數(shù)控制因子，可達(dá)到縮短收斂時(shí)間、提高收斂速度的目的。

2.2.2 PCF-PLL跟蹤誤差

由PLL的跟蹤誤差公式可推導(dǎo)得出PCF-PLL的3跟蹤誤差表達(dá)式為

3=3+

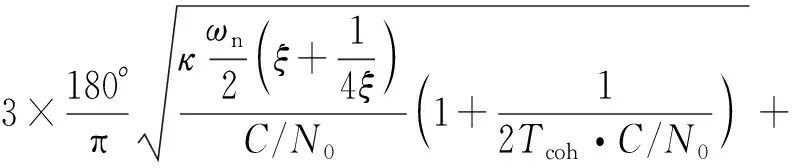
(23)

式中，為輸入信號(hào)的載噪比；為相干積分時(shí)間；為載波L1的波長(zhǎng)；為衛(wèi)星和接收機(jī)的連線距離。

由式(23)可得，環(huán)路跟蹤誤差主要跟環(huán)路的熱噪聲誤差有關(guān)。通過(guò)控制參數(shù)控制因子可有效地控制環(huán)路跟蹤誤差，減小參數(shù)控制因子，環(huán)路跟蹤誤差隨之降低。

由上述分析可得，當(dāng)參數(shù)控制因子>1時(shí)，PCF-PLL的跟蹤誤差及收斂速度都優(yōu)于PLL；參數(shù)控制因子與環(huán)路收斂速度正相關(guān)，與環(huán)路跟蹤誤差正相關(guān)。環(huán)路最優(yōu)參數(shù)控制因子的選擇應(yīng)滿足保證跟蹤精度的前提下，使收斂速度盡可能快。下面將詳細(xì)分析參數(shù)控制因子最優(yōu)值的選擇。

2.3 PCF-PLL參數(shù)控制因子κ最優(yōu)值的選擇

環(huán)路跟蹤誤差為環(huán)路性能評(píng)估的首要指標(biāo)，故在選擇參數(shù)控制因子時(shí)，首先考慮其約束作用。為選擇一個(gè)合適的參數(shù)控制因子，將分析不同載噪比下，參數(shù)控制因子與環(huán)路跟蹤誤差的關(guān)系。

參數(shù)控制因子的選擇首先要滿足環(huán)路跟蹤誤差小于跟蹤門限，對(duì)環(huán)路跟蹤門限的保守估計(jì)為環(huán)路3跟蹤誤差小于其1/4鑒相牽入范圍(90°)，即

3<225°

(24)

不同載噪比及動(dòng)態(tài)多普勒下，環(huán)路誤差特性曲線如圖5所示。

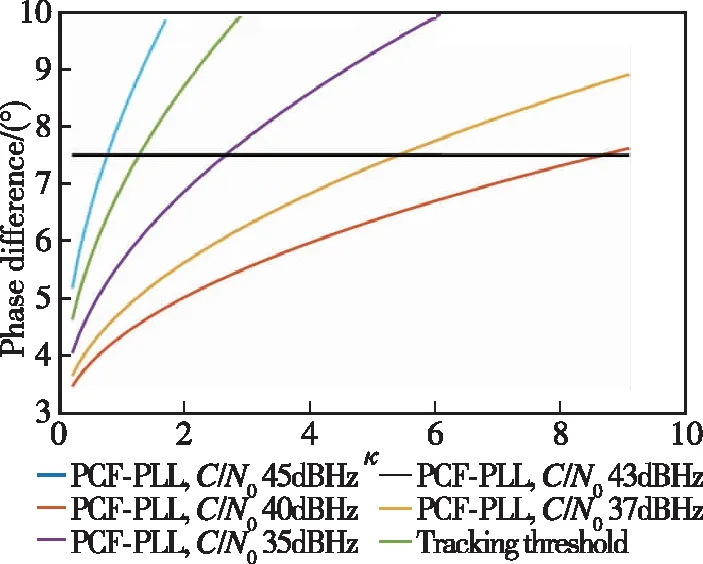
圖5 不同載噪比C/N0及動(dòng)態(tài)多普勒下誤差特性曲線Fig.5 Error characteristics under different carrier-to-noise C/N0 and dynamic Doppler

由圖5可得，載噪比與參數(shù)控制因子范圍對(duì)應(yīng)關(guān)系如表2所示。

表2 載噪比與參數(shù)控制因子

由圖5和表2可得，隨著載噪比的降低，環(huán)路參數(shù)控制因子的范圍越來(lái)越小。當(dāng)信號(hào)載噪比降至35dBHz時(shí)，參數(shù)控制因子已不能優(yōu)化環(huán)路性能。

由以上分析可得，參數(shù)控制因子的增大，雖會(huì)造成跟蹤誤差的增大，但可以很好地消除高動(dòng)態(tài)引起的誤差以及縮短跟蹤高動(dòng)態(tài)信號(hào)時(shí)環(huán)路收斂的時(shí)間。故而當(dāng)高動(dòng)態(tài)應(yīng)力較小時(shí)，參數(shù)控制因子值應(yīng)盡可能小；反之，當(dāng)高動(dòng)態(tài)應(yīng)力較大時(shí)，參數(shù)控制因子值應(yīng)盡可能大。

3 仿真校驗(yàn)

本節(jié)將仿真驗(yàn)證PCF-PLL對(duì)GNSS-LEO信號(hào)跟蹤的有效性，并從環(huán)路跟蹤誤差和環(huán)路收斂時(shí)間兩方面評(píng)估PCF-PLL性能，同時(shí)驗(yàn)證理論推導(dǎo)的PCF-PLL參數(shù)控制因子最優(yōu)取值區(qū)間。環(huán)路基本仿真參數(shù)如表3所示。

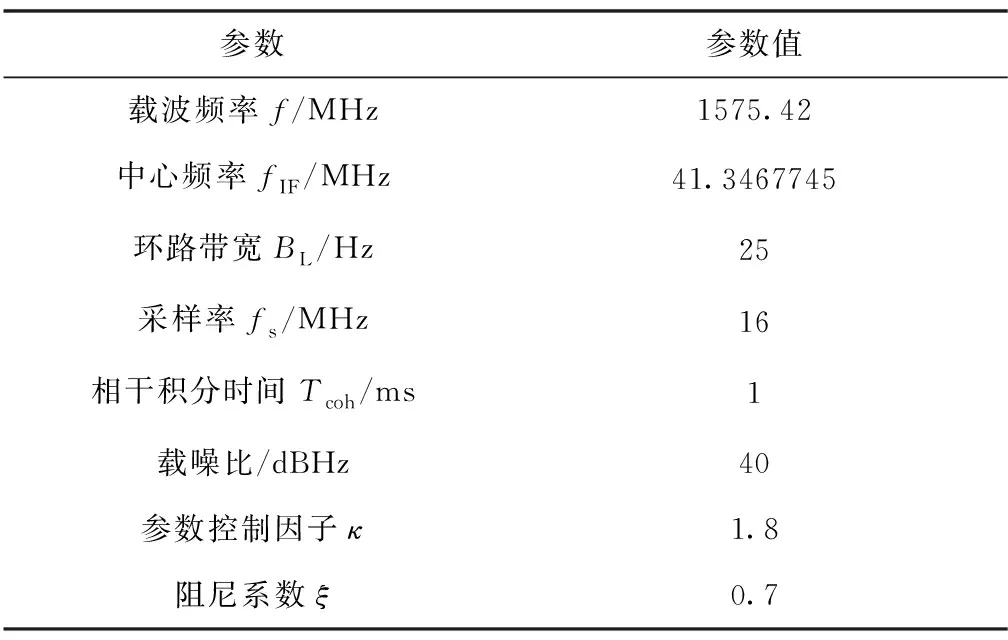
表3 PCF-PLL仿真參數(shù)

3.1 PCF-PLL有效性驗(yàn)證

通過(guò)對(duì)PCF-PLL整個(gè)可見周期及前1500ms跟蹤誤差的仿真實(shí)驗(yàn)，評(píng)估PCF-PLL的有效性。為此，設(shè)置了2組實(shí)驗(yàn)：1)選取LEO-GPS01的一次可見周期進(jìn)行仿真分析，評(píng)估其跟蹤穩(wěn)定性和魯棒性，其輸入信號(hào)存在動(dòng)態(tài)多普勒信息，最大多普勒頻移可達(dá)40kHz，載波多普勒變化率最大不超過(guò)60Hz/s，載波多普勒加速率范圍為[0Hz/s～0.15Hz/s]；2)取第一組實(shí)驗(yàn)前1500ms數(shù)據(jù)，在不同環(huán)路帶寬(25Hz/15Hz)下進(jìn)行仿真分析，評(píng)估其跟蹤收斂時(shí)間和跟蹤精度，其輸入信號(hào)動(dòng)態(tài)特性同1)。實(shí)驗(yàn)1)的載波頻率跟蹤誤差曲線如圖6所示。

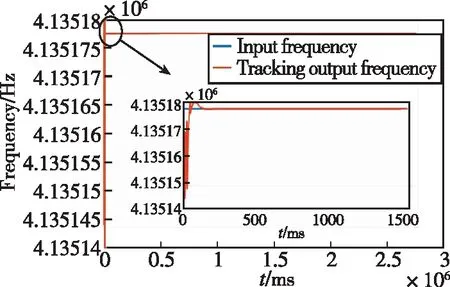
圖6 PCF-PLL頻率跟蹤誤差Fig.6 Tracking error of PCF-PLL frequency

由圖6可得，PCF-PLL在整個(gè)可見周期內(nèi)，能夠穩(wěn)定跟蹤含動(dòng)態(tài)多普勒信息的GNSS-LEO信號(hào)，證明了PCF-PLL的跟蹤穩(wěn)定性；且從跟蹤結(jié)果來(lái)看，由參數(shù)控制因子決定的環(huán)路狀態(tài)切換機(jī)制并未引起跟蹤上的較大波動(dòng)，證明了PCF-PLL的魯棒性。綜合來(lái)看，PCF-PLL可實(shí)現(xiàn)大多普勒頻移跟蹤、快速入鎖，跟蹤精度較好。

整個(gè)可見周期前1500ms內(nèi)，PCF-PLL跟蹤階段環(huán)路帶寬和PLL環(huán)路帶寬均為25Hz，參數(shù)控制因子為1.8時(shí)，PCF-PLL與PLL跟蹤結(jié)果如圖7所示。

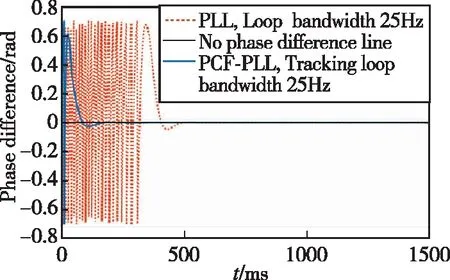
圖7 PCF-PLL與PLL跟蹤相位差Fig.7 Tracking phase error between PCF-PLL and PLL

從圖7中可以看出，當(dāng)PCF-PLL跟蹤階段環(huán)路帶寬和PLL環(huán)路帶寬均為25Hz時(shí)，PLL雖然也能在1500ms內(nèi)跟蹤上輸入信號(hào)，但其入鎖時(shí)間過(guò)長(zhǎng)，超過(guò)500ms，影響了接收機(jī)的即時(shí)性；而PCF-PLL能極大地縮短入鎖時(shí)間，降至110ms以內(nèi)，且跟蹤精度不亞于二階鎖相環(huán)。

整個(gè)可見周期前1500ms內(nèi)，PCF-PLL跟蹤階段環(huán)路帶寬和PLL環(huán)路帶寬均為15Hz，參數(shù)控制因子為1.8時(shí)，PCF-PLL與PLL前1500ms跟蹤結(jié)果如圖8所示。

圖8 PCF-PLL與PLL跟蹤相位差Fig.8 Tracking phase error between PCF-PLL and PLL

從圖8中可以看出，當(dāng)PCF-PLL跟蹤階段環(huán)路帶寬和PLL環(huán)路帶寬均為15Hz時(shí)，PLL不能在1500ms內(nèi)跟蹤上輸入信號(hào)，入鎖困難；而PCF-PLL能實(shí)現(xiàn)1500ms內(nèi)入鎖，且跟蹤誤差小。

GNSS-LEO可見時(shí)間短，可見次數(shù)多，故星載接收機(jī)在捕獲、跟蹤中需要頻繁換星，且信號(hào)伴隨動(dòng)態(tài)多普勒頻移，其對(duì)即時(shí)、穩(wěn)定跟蹤要求更高。而PLL在這種狀況下，存在入鎖困難、失鎖后重新入鎖的時(shí)間較長(zhǎng)等問(wèn)題，顯然是無(wú)法滿足要求的。PCF-PLL則通過(guò)一個(gè)簡(jiǎn)單的切換機(jī)制及時(shí)調(diào)整環(huán)路狀態(tài)，很好地解決了這個(gè)問(wèn)題。

3.2 PCF-PLL參數(shù)優(yōu)化仿真分析

通過(guò)對(duì)不同信噪比下環(huán)路收斂時(shí)間進(jìn)行仿真分析，進(jìn)一步驗(yàn)證了PCF-PLL參數(shù)控制因子優(yōu)化策略，并對(duì)其進(jìn)行了修正。由前面的理論分析可知，參數(shù)控制因子與信號(hào)動(dòng)態(tài)性能和跟蹤誤差要求有關(guān)。通過(guò)對(duì)不同參數(shù)控制因子的仿真分析，驗(yàn)證了理論部分對(duì)參數(shù)控制因子的優(yōu)化策略的有效性。設(shè)置PCF-PLL跟蹤階段環(huán)路帶寬和PLL環(huán)路帶寬均為25Hz，參數(shù)控制因子與牽引階段環(huán)路帶寬的對(duì)應(yīng)關(guān)系，如表4所示。

表4 參數(shù)控制因子κ與環(huán)路帶寬

根據(jù)表4數(shù)據(jù)，仿真得到PCF-PLL不同參數(shù)控制因子下的跟蹤誤差曲線，如圖9所示。

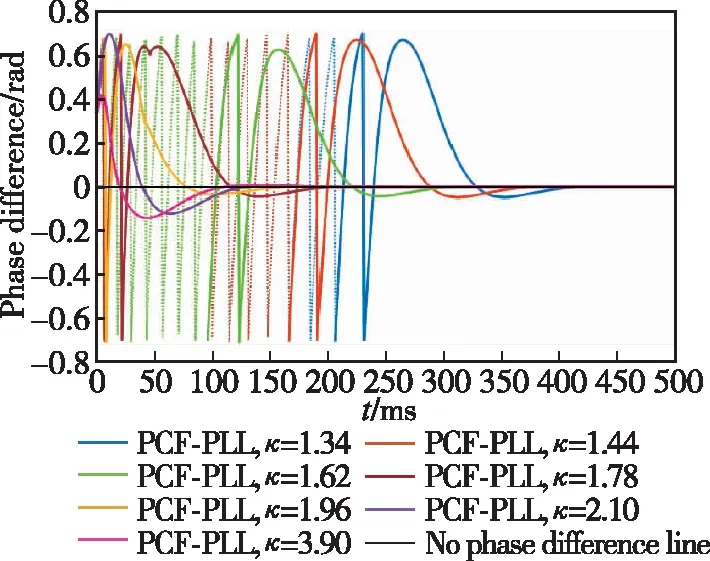
圖9 PCF-PLL不同參數(shù)控制因子κ下跟蹤相位誤差Fig.9 Tracking phase error under different PCF-PLL parameters

從圖9中可以看出，在參數(shù)控制因子理論最優(yōu)范圍[1, 2.6]內(nèi)，隨著參數(shù)控制因子的增大，環(huán)路收斂時(shí)間加快100～200ms，可實(shí)現(xiàn)快速入鎖，且跟蹤誤差均較小;但參數(shù)控制因子越大，環(huán)路帶寬越大，牽引階段環(huán)路引入的噪聲越多，牽引階段的信噪比SNR下降越嚴(yán)重。可見，參數(shù)控制因子的選擇要權(quán)衡收斂速度和信噪比SNR。

為保證信號(hào)質(zhì)量，優(yōu)化環(huán)路性能，加入收斂時(shí)間作為約束條件，進(jìn)一步優(yōu)化參數(shù)控制因子的最優(yōu)范圍。仿真得到不同參數(shù)控制因子下PCF-PLL收斂時(shí)間與參數(shù)控制因子的特性曲線，如圖10所示。

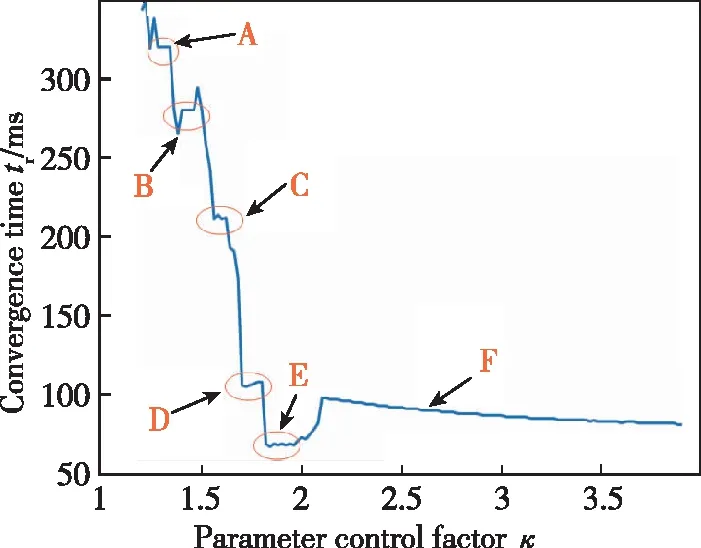
圖10 參數(shù)控制因子κ與收斂時(shí)間trFig.10 PCF κ and convergence time tr

由圖10可得，隨著參數(shù)控制因子的增大，收斂時(shí)間總體呈下降趨勢(shì)，但存在一定起伏波動(dòng)，可分為6個(gè)階段，依次為圖10中標(biāo)示的A、B、C、D、E、F。各階段參數(shù)控制因子對(duì)應(yīng)的牽引階段環(huán)路帶寬及收斂時(shí)間如表5所示。

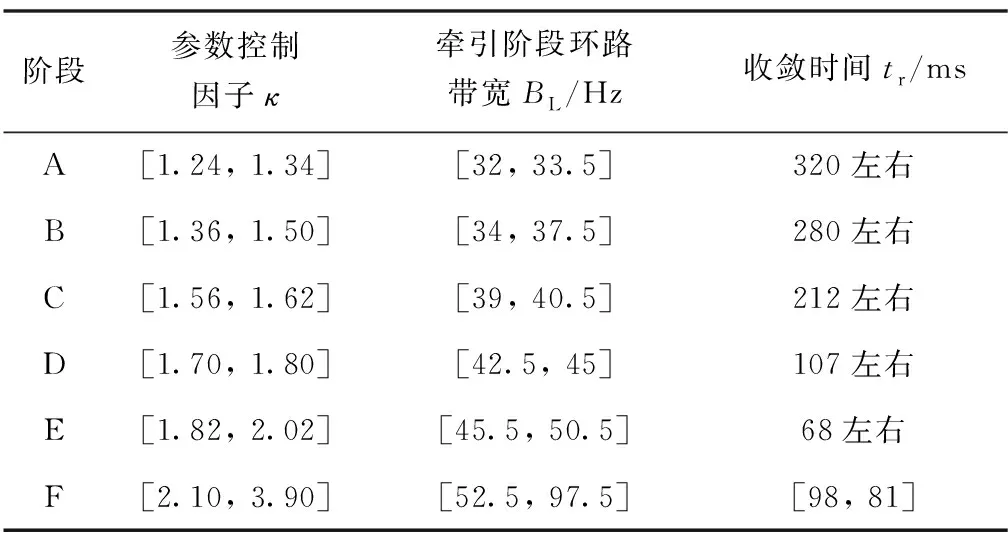
表5 各階段參數(shù)表

由圖10和表5可得，參數(shù)控制因子在收斂速度和信噪比的權(quán)衡中存在一個(gè)最優(yōu)階段，即E階段，此時(shí)收斂速度最快，信噪比為0.8dB左右，且滿足跟蹤門限的要求。此后，增大參數(shù)控制因子對(duì)于縮小環(huán)路收斂時(shí)間的控制效果已不顯著。

由上述分析可知，在低軌星載的高動(dòng)態(tài)環(huán)境下，PCF-PLL環(huán)路帶寬為25Hz、相干積分時(shí)間為1ms時(shí)，參數(shù)控制因子的最優(yōu)范圍為[1.82, 2.02]，可跟蹤信號(hào)最低至35dBHz;而三階鎖相環(huán)環(huán)路帶寬為18Hz、相干積分時(shí)間為1ms時(shí)，環(huán)路最低跟蹤信號(hào)約為35dBHz，與PCF-PLL相當(dāng)。綜上所述，采用PCF-PLL可提高PLL的動(dòng)態(tài)適應(yīng)能力，其入鎖時(shí)間可縮短78%，環(huán)路收斂速度更快，在保證跟蹤精度的同時(shí)，提高了環(huán)路對(duì)于低信噪比跟蹤信號(hào)的跟蹤能力，且環(huán)路階數(shù)低，有利于硬件實(shí)現(xiàn)。

4 結(jié)論

本文首先分析了GNSS-LEO信號(hào)特性，并在動(dòng)態(tài)環(huán)境下，針對(duì)低軌星載接收機(jī)存在的大多普勒頻移問(wèn)題及頻繁快速換星的實(shí)時(shí)性要求，提出了一種基于參數(shù)控制的載波跟蹤算法，理論分析及仿真結(jié)果表明：

1)該算法可實(shí)現(xiàn)低軌星載狀態(tài)的動(dòng)態(tài)多普勒GNSS-LEO信號(hào)整個(gè)可見周期的跟蹤，期間無(wú)失鎖現(xiàn)象。

2)該算法基于動(dòng)態(tài)多普勒狀態(tài)，通過(guò)調(diào)整參數(shù)控制因子控制環(huán)路濾波器狀態(tài)，可實(shí)現(xiàn)動(dòng)態(tài)多普勒環(huán)境下的快速入鎖，持續(xù)穩(wěn)定跟蹤。

3)結(jié)合信號(hào)載噪比、收斂時(shí)間和收斂誤差等條件，從理論上推導(dǎo)了參數(shù)控制因子的最優(yōu)范圍，仿真結(jié)果驗(yàn)證了其正確性。

4)該算法簡(jiǎn)單易行地解決了低軌衛(wèi)星運(yùn)行環(huán)境下GNSS-LEO信號(hào)的多普勒問(wèn)題，同時(shí)滿足實(shí)時(shí)穩(wěn)定性要求，有利于硬件實(shí)現(xiàn)。