基于功率特征分組的空時自適應脈沖干擾抑制方法

劉 鵬，王 盾，高文寧

(航天恒星科技有限公司，北京 100095)

0 引言

隨著導航電子對抗技術的發展，軍用導航接收機面臨著越來越多的電磁干擾。由于衛星導航信號到達地面時極其微弱，僅靠信號本身的擴頻增益無法保證接收機在強干擾環境下正常工作，必須借助其他的抗干擾措施。

脈沖干擾是一種常見的干擾類型，由持續時間短、信號幅度大的不規則脈沖或噪聲尖峰組成，通常具有較寬的頻譜。按照產生機理，脈沖干擾可分為兩類，一類是由于大氣中的雷暴現象等產生的自然干擾；一類是由高頻電子設備如繼電器、雷達、干擾源等產生的人為干擾。其中L頻段雷達和L頻段的脈沖干擾源極易對導航信號產生影響。

由于脈沖干擾的高帶寬、突發性等特點，脈沖干擾抑制具有較大難度。針對脈沖干擾的抑制，主要有時域、頻域、空域以及多域聯合濾波算法。其中，時域、頻域濾波算法主要針對窄帶干擾，而脈沖干擾通常占據較寬的頻帶，因此，時域、頻域濾波算法對脈沖干擾的抑制效果會變差或失效。雖然脈沖消隱(Pulse Blanking)方法對干擾帶寬不敏感，但仍然會造成信號能量的損失。陣列信號處理算法主要包含空域自適應處理(Spatial Adaptive Processing，SAP)、空時自適應處理(Space-Time Adaptive Proces-sing，STAP)以及空頻自適應處理(Space-Frequency Adaptive Processing，SFAP)等類型，具有更強的抗干擾能力以及更小的信號衰減，在衛星導航接收機的研制過程中得到了廣泛應用。陣列信號處理濾波權值的求取方法主要包括塊處理算法和連續處理算法兩種，塊處理算法為無反饋開環處理，權值計算無收斂過程，因此得到了大量應用。然而，常規的陣列信號塊處理算法通常假設干擾的統計特征是平穩的，利用當前的信號采樣數據計算濾波權值，對當前和后續采樣數據進行干擾抑制。一方面，由于脈沖干擾的突發性，當計算濾波權值的數據塊中不包含脈沖干擾，而脈沖干擾恰好出現在后續數據中時，將無法對脈沖干擾進行有效抑制；另一方面，即使計算濾波權值的數據塊中包含脈沖干擾，由于可能僅是一部分時段的信號采樣數據包含了脈沖干擾，據此計算的干擾零陷深度也會受到影響，從而影響算法的抗干擾能力。

針對以上問題，本文通過功率檢測對接收數據進行分組，改進常規空時自適應處理算法，提升其對脈沖干擾的抑制能力。首先，對接收數據進行功率檢測，判斷當前信號采樣數據塊是否包含干擾；其次，根據檢測結果將數據塊進行分組，分為有干擾數據組和無干擾數據組；隨后，利用有干擾數據組計算濾波權值，濾除其中的干擾信號，對于無干擾數據組，則將濾波權值固定為常數，保留其中的有效信號成分；最后將濾波后的兩組數據按照采樣順序重新進行合并輸出。通過數據分組，提高了干噪比的統計計算準確度，增加了干擾零陷深度，從而實現了抗干擾能力的提升。

本文結構如下：第1節介紹常規空時自適應處理算法，并分析其在脈沖干擾抑制中存在的問題；第2節提出功率特征分組空時自適應處理方法，并分析其對脈沖干擾抑制性能的提升；第3節對本文提出的方法與常規算法進行仿真分析及性能對比；第4節為結論。

1 常規空時自適應處理算法及存在問題

1.1 常規空時自適應處理算法概述

空時自適應處理的結構框圖如圖1所示，陣列包含個天線單元，每個單元后有-1個時間延遲線，則STAP接收數據模型可表示為

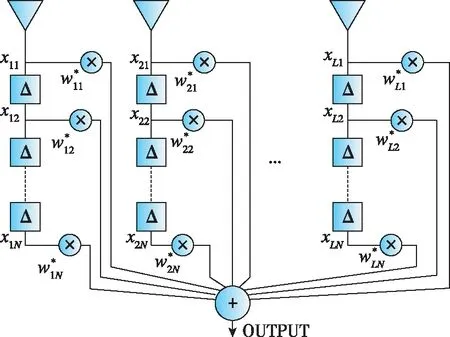
圖1 空時自適應處理框圖Fig.1 Space-time adaptive processing block diagram

()=()+()+()

(1)

其中，=[,…,1,,…,2,…,1,…，]為×1空時數據向量，上標T表示向量轉置；()為導航信號復包絡向量，()=[(),(),…,()]，()為第個導航信號的復包絡；為信號陣列空時流形矩陣，=[1,2,…,]，為第個導航信號的空時導向矢量；()為干擾復包絡向量，()=[(),(),…,()]，()為第個干擾的復包絡；為干擾陣列空時流形矩陣，=[1,2,…,]，為第個干擾的空時導向矢量；()為陣列噪聲向量。

陣列的協方差矩陣定義為

=E[()()]

(2)

式中，E[·]表示求期望值，上標H表示向量共軛轉置。

空時自適應處理的濾波權值為

=μ

(3)

其中，為常數；為約束矢量。

則經空時自適應處理后的輸出為

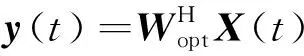
(4)

1.2 脈沖干擾抑制問題分析

假設脈沖干擾為一個時間連續的帶內干擾與占空比為1(>1)的周期矩形脈沖的乘積，干擾表示為

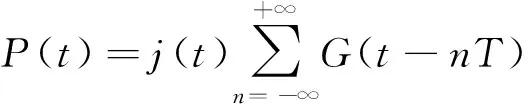
(5)

式中，()為時間連續干擾的復包絡；()為持續時間為、占空比為1的矩形脈沖，表示為

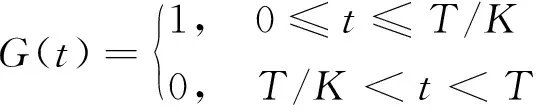
(6)

當天線陣列接收到式(5)所示的一個干擾時，并假設信號、干擾與噪聲不相關，則協方差矩陣為

=E[()()]

(7)

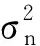
由式(5)得

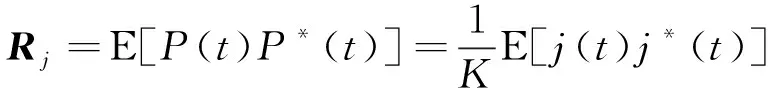
(8)

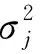
由于信號功率遠低于干擾和噪聲功率，綜合式(7)、式(8)并將信號分量省略，得

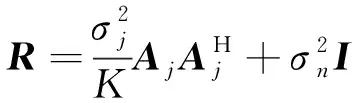
(9)

對協方差矩陣進行特征值分解，得

(10)

將特征值按照從大到小的順序排列，由式(9)、式(10)得

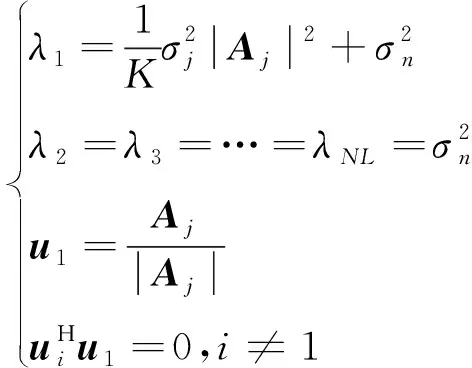
(11)

其中，為干擾特征值；為干擾特征向量；其余為噪聲特征值和噪聲特征向量。干擾方向的陣列響應為

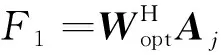
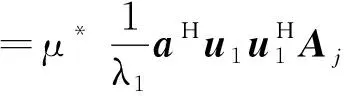
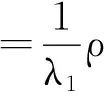
(12)

其中

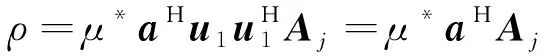
(13)

由式(11)和式(12)，當干擾功率遠大于噪聲功率時

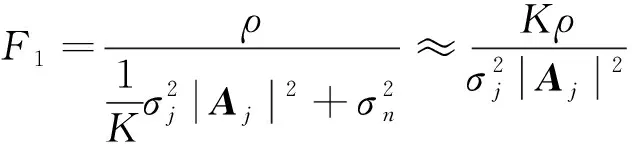
(14)

由上述分析可見，空時自適應處理的干擾抑制能力與干擾特征值成正比，干擾特征值越大，零陷越深，干擾抑制能力越強。常規空時自適應處理算法未對有干擾數據和無干擾數據進行區分，統一進行協方差矩陣估計及權值計算。一方面，由式(11)，干擾特征值與脈沖干擾的占空比成正比，當脈沖占空比較低時，將導致零陷深度降低，抗干擾能力下降；另一方面，在工程實現過程中，用于協方差矩陣估計的數據是有限的，當脈沖占空比降低到一定程度后，將出現用于協方差矩陣估計的數據不包含干擾的情況，此時如果利用當前數據塊計算的權值對后續數據進行干擾抑制，甚至會出現抗干擾失效的問題。

2 功率特征分組空時自適應處理方法

2.1 方法描述

針對以上問題，本文提出了一種基于功率特征分組的空時自適應處理方法，以提高對脈沖干擾的抑制能力。

該方法的實現步驟如下：

步驟一：對輸入數據進行功率檢測，根據檢測結果將數據分為兩組，即有干擾數據和無干擾數據，兩組數據分別表示為

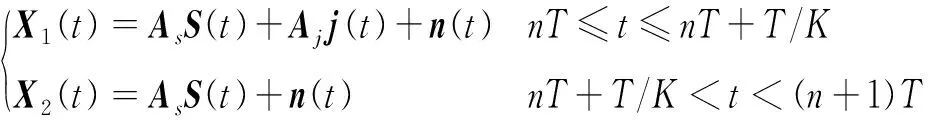
(15)

干擾檢測的閾值需要在虛警概率和漏警概率之間進行折中，本文的閾值設為噪聲功率增加3dB。

步驟二：將數據進行分組后，分別計算兩組數據的濾波權值。第一組數據包含干擾，權值計算包含協方差矩陣估計和逆矩陣與約束向量相乘2個過程。

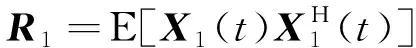
(16)

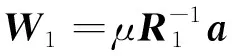
(17)

實現過程中，需要緩存一段數據并利用有限采樣點對協方差矩陣進行估計，在數據緩存段內采樣點可以跨周期。當脈沖干擾占空比較小，緩存的數據點數不足時，則考慮減少統計點數或增加第二組的數據采樣點。

第二組數據無干擾，但為了保證濾波延遲的一致性，仍然對第二組數據進行濾波處理，其濾波權值為

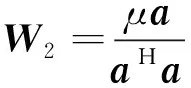
(18)

步驟三：利用權值對分組數據進行自適應濾波

(19)

步驟四：將濾波后的分組數據合并輸出

(20)

2.2 抗干擾性能分析

數據分組后，只有第一組數據存在干擾，因此對第一組數據的抗干擾性能進行分析。

由式(15)、式(16)得

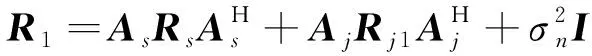
(21)

1為干擾期望功率，其值為

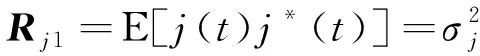
(22)

省略導航信號分量，協方差矩陣為

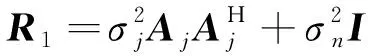
(23)

對進行特征值分解，得

(24)

將特征值按照從大到小的順序排列，由式(23)、式(24)得

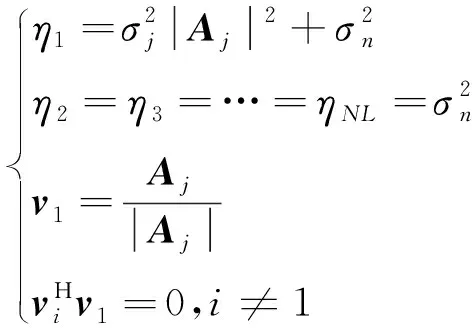
(25)

其中，為干擾特征值；為干擾特征向量；其余為噪聲特征值和噪聲特征向量。干擾方向的陣列響應為

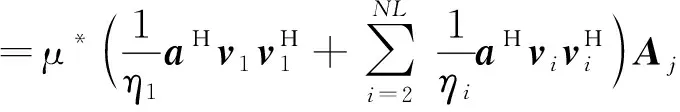
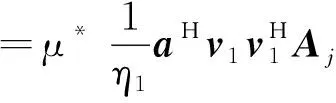
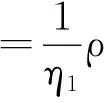
(26)

其中

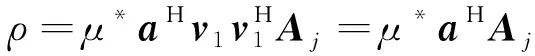
(27)

由式(25)和式(26)，當干擾功率遠大于噪聲功率時

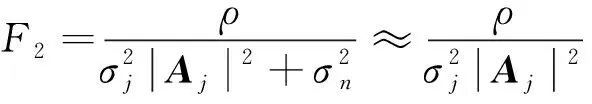
(28)

由式(14)和式(28)，本文提出的算法在進行自適應濾波后，干擾方向在相應頻帶的陣列響應幅值更低，可獲得更深的干擾零陷，因此具有更強的抗干擾能力，性能提升增益值為

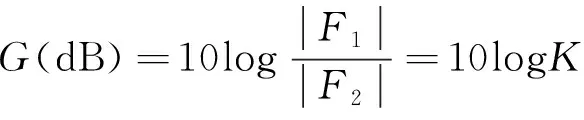
(29)

需要說明的是，式(29)是算法的期望增益，實際增益需要具體分析，分析極限情況可見：

1)當趨近于1，即脈沖干擾占空比趨近于100%，脈沖干擾趨近于時間連續干擾時，性能提升增益值趨近于0；而當=1時，干擾已經變為時間連續干擾，所有數據均在分組1，此時改進算法的處理過程與常規算法相同，而算法性能增益為0。上述結果與式(29)相符。

2)當趨近于無窮大，即脈沖干擾占空比趨近于0時，由于僅有極少的數據在分組1，此時計算協方差矩陣需要減少統計點數或增加第二組的數據采樣點，因此實際增益值會低于期望值。

3 仿真實驗

導航信號中心頻率設置為BDS B3頻點，陣列為四陣元方陣，天線單元間距為半波長。信號下變頻后的模擬中心頻率為15.48MHz，采樣頻率為62MHz。空時自適應處理每個天線陣子后采用3個時域抽頭，協方差矩陣估計點數為4096，權值計算采用自適應調零算法。

接收導航信號的信噪比設置為-25dB，并施加1個脈沖干擾，干擾來向為方位角120°、俯仰角45°。由于實際抗干擾測試通常設置脈沖周期為10μs～100μs，為便于分析，本文將脈沖干擾的1個周期設置為對應4096個采樣點，即脈沖周期約為66μs，并將脈沖干擾占空比設置為25%。則采用常規空時自適應處理時，1次協方差矩陣估計對應1個脈沖干擾周期。而采用本文提出的改進算法，當對完成分組后的有干擾數據進行協方差矩陣估計時，1次估計需要用到4個脈沖干擾周期的數據。

對協方差矩陣進行特征值分解，最大的特征值為干擾特征值，其余特征值為噪聲特征值。由于噪聲特征值基本穩定，因此可以用干擾特征值和噪聲特征值的比值(INR)來表征干擾特征值的變化趨勢。設置干信比(ISR)從60dB逐漸增大到100dB，由特征分解得到的兩種算法的干噪比如圖2所示，干擾方向的陣列響應幅值如圖3所示。

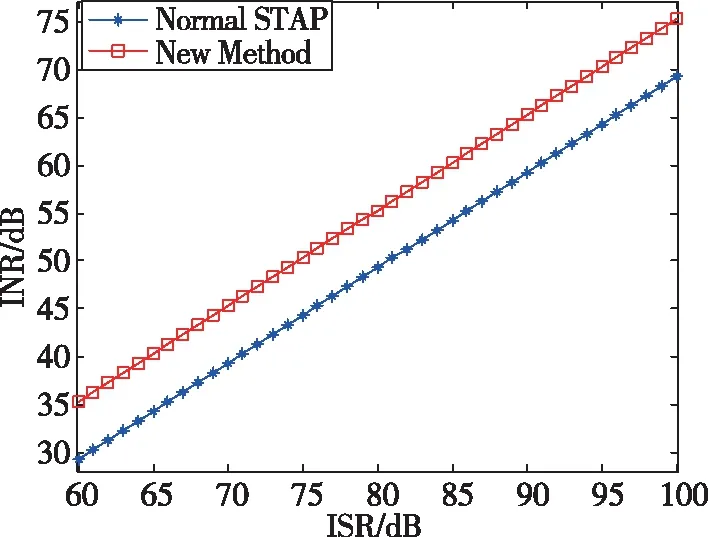
圖2 干擾特征值分析Fig.2 Interference eigenvalue analysis

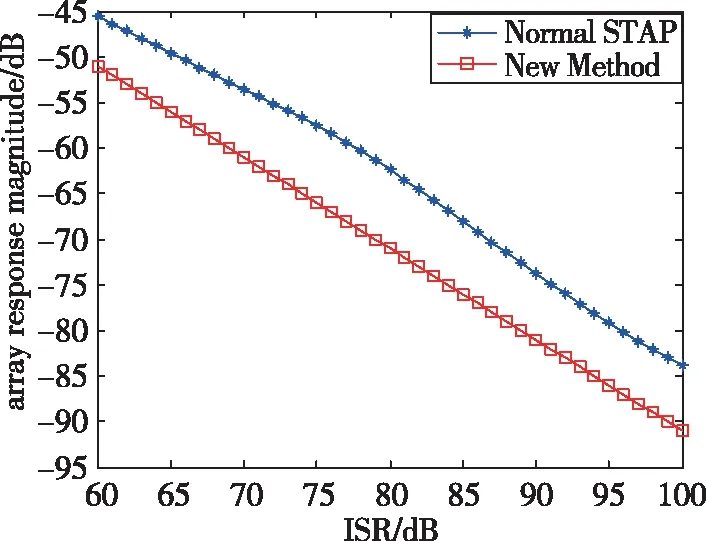
圖3 干擾方向陣列響應幅值Fig.3 Array response magnitude in the interference direction

可見，當脈沖干擾占空比為25%時，本文算法的干擾特征值相比原算法增加約6dB，干擾方向的陣列響應幅值降低約6dB，即零陷深度增加約6dB，仿真結果與理論分析一致。

將方位角固定為干擾方位角，當干信比分別為70dB、80dB、90dB和100dB時，兩種算法的陣列響應幅值隨俯仰角的變化情況如圖4所示。由圖4可見，兩種算法均能在干擾方向形成明顯的零陷，但相比常規空時自適應處理，本文方法的零陷深度更低，在不同干信比條件下相比原算法均增加約6dB。

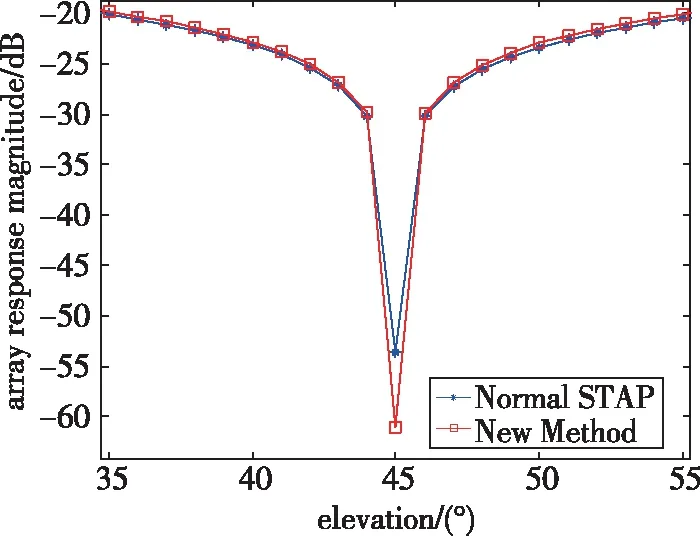
(a)干信比70dB

4 結論

本文對常規空時自適應處理算法進行了介紹，分析了常規算法在脈沖干擾抑制中存在的問題，在此基礎上，提出了一種基于功率特征分組的空時自適應處理方法,并對該方法的性能進行了理論和數據仿真分析，結果表明：

1)通過功率檢測將采樣數據進行分組處理，可提升接收脈沖干擾時干噪比的統計計算準確度，增加干擾零陷深度，實現抗干擾能力的提升。

2)常規算法和本文算法的性能分析結果表明，本文算法的性能提升期望增益值與脈沖干擾的占空比倒數成正比。

3)仿真結果與理論分析一致，證明了該方法的有效性。同時，本文所提算法與常規空時自適應處理算法相比，處理復雜度基本一致，具有較強的工程應用價值。