P2構型PHEV模型預測能量管理策略研究

羅 勇，趙 爽，龐 維，黃 歡

(重慶理工大學 汽車零部件先進制造技術教育部重點實驗室， 重慶 400054)

插電式混合動力汽車(plug-in hybrid electric vehicle,PHEV)的能量管理策略通過協調發動機和電機的轉矩，實現節能減排。目前，插電式混合動力汽車的能量管理策略可分為基于規則的控制策略和基于優化理論的控制策略兩大類。基于規則的控制策略，如電量消耗-保持[1]、模糊控制[2]等，依據工程經驗設定工作模式和模式切換條件，通過模式組合來降低油耗，但其規則制定依賴于工程經驗，難以保證最優控制。基于優化理論的控制策略，如基于等效油耗最小的能量管理策略[3-4]，通過引入油電等效因子，建立油耗等效函數，然后計算出當前燃油經濟性最優的動力分配關系，實現瞬時的最優控制，但無法保證在整個工況的能耗最優；基于最優理論中動態規劃算法[5-6]的能量管理策略依賴未來全部工況已知，但整個行駛工況獲取困難，且計算量大，無法單獨運用到實時控制中。

近年來，將瞬時最優和全局最優結合在一起的預測控制策略受到國內外學者們的關注。該方法的控制效果主要依賴對未來車速的有效預測。荊紅娟[7]假設未來車速呈指數變化，然而駕駛員操作的隨機性使該預測方法不適用于實際工況。Chao等[8]建立了基于馬爾科夫鏈和神經網絡的車速預測模型，結果表明前者的車速預測精度不及后者。韓少劍等[9]基于車聯網技術，實時獲取交通信息，對未來車速進行預測，提高了車速預測精度，但不適用于沒有ITS/GIS等智能交通系統的車輛。徑向基神經網絡具有適應能力強、計算速度快的特點，本文采用徑向基神經網絡對車速進行預測，以提高預測的準確性和實時性，進而改善預測控制策略節能效果。

以某P2構型插電式混合動力汽車為研究對象，對采用徑向基神經網絡進行車速預測的預測能量管理策略展開研究。首先建立基于徑向基神經網絡的車速預測模型，并以7種標準循環工況數據為訓練樣本對神經網絡進行訓練，對其預測準確性進行驗證和評估；在車速預測模型的基礎上，在預測時域內采用動態規劃算法對最優控制量進行求解，實現動力源的最優轉矩分配；最后建立系統仿真模型，在典型循環工況下對該策略的控制效果進行仿真分析。

1 系統構型和整車參數

以P2構型混合動力系統為研究對象，其結構如圖1所示。動力傳動系統由發動機、驅動電機、離合器、自動機械式變速器等部件組成，各部件同軸相連，通過對離合器的控制，實現工作模式的切換。表1為整車和關鍵動力部件參數。

圖1 P2構型PHEV系統結構示意圖

表1 整車和動力零部件參數

2 神經網絡車速預測

2.1 BP神經網絡模型

BP神經網絡是一種多層前饋神經網絡，由輸入層、隱含層和輸出層構成，網絡結構如圖2所示。其隱含層有不同層數，層數的選擇視不同問題選取，合適的層數可以提高預測精度。各層神經元之間完全連接但同層之間不連接，各連接強度不同。

圖2 BP神經網絡結構示意圖

BP神經網絡輸出計算公式如下：

(1)

(2)

式中：Xi為輸入層第i個節點的輸出值；Yj為中間層第j個節點的輸出；Zk為輸出層第k個節點的輸出；Wij為輸入層第i個節點到隱含層第j個節點的權值；Wjk為中間層第j個節點到輸出層第k個節點的權值；θj和θk分別為中間層第j個節點和輸出層第k個節點的閾值。

2.2 RBF神經網絡結構

RBF神經網絡是一種局部逼近網絡，與其他神經網絡相比，其收斂速度快且計算量小，車速預測結果和實時性也更好[10]。其由輸入層、隱藏層和輸出層構成，結構如圖3所示。輸入層輸入數據；隱藏層主要為徑向基函數，它將輸入層的輸出通過非線性變換映射到一個新的區域；輸出層將隱藏層的輸出進行線性求和輸出。

圖3 RBF神經網絡結構示意圖

變換函數采用高斯函數，可表示為：

(3)

式中：xk為第k個樣本輸入；ci為基函數中心；σi為高斯函數的標準差；‖xk-ci‖2為歐式范數。

RBF神經網絡輸出為：

(4)

式中：wij為隱含層至輸出層的權值；i=1，2,…,m，m為隱藏層節點數；j=1，2,…,n，n為輸出向量維數；ykj為第k個輸入對應的輸出。

2.3 車速預測結果分析

通過上述建立的RBF與BP神經網絡模型對未來車速進行預測，預測模型如式(5)所示：

[Vt+1，Vt+2,…，Vt+p]=f(Vt-p，Vt-p+1，…,Vt)

(5)

式中：p為神經網絡輸入層維數。選用WLTC、HWFFT、LA92、US06、UDDS、China urban、JC08工況為訓練集，NEDC工況為測試集，訓練集和測試集數據如圖4、5所示。

圖4 訓練集車速

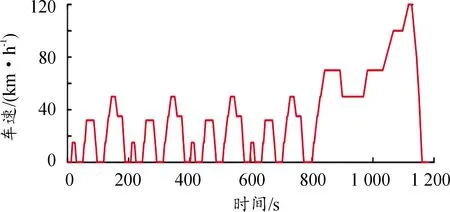
圖5 測試集車速

在不同時域下，采用2種車速預測模型對車速進行預測。圖6是2種車速預測模型在預測時域為10 s的對比結果。由圖6(a)和6(b)可以看出，2種預測方法的車速預測結果趨勢一致，車速結果接近。由圖6(c)和6(d)可見，工況變化前后，2種預測結果與實際車速偏離幅度接近；對下一秒的預測結果而言，BP網絡的誤差遠大于RBF網絡。

為更合理地評價車速預測結果，選用均方根誤差作為評價指標[11-12]，其數學表達式如下：

(6)

(7)

式中：R(k)為k時刻預測時域內均方根誤差；Re為整個工況均方根誤差；p為預測時長；v(k+i)為k時刻下預測時域內k+i時刻的預測車速；vr(k+i)為k+i時刻測試集車速；S為測試集時長。Re的大小與預測精度為負相關，Re越小，則預測精度越高。

圖6 車速預測結果對比

由表2可知：在5個預測時域下，RBF網絡都有更小的均方根誤差；而隨著預測時域的減小，2種預測方法的均方根誤差隨之減小，預測效果更好。

表2 車速預測指標

3 PHEV的預測控制策略

3.1 預測控制能量管理策略求解

本文所提出的預測控制能量管理策略求解流程如圖7所示。

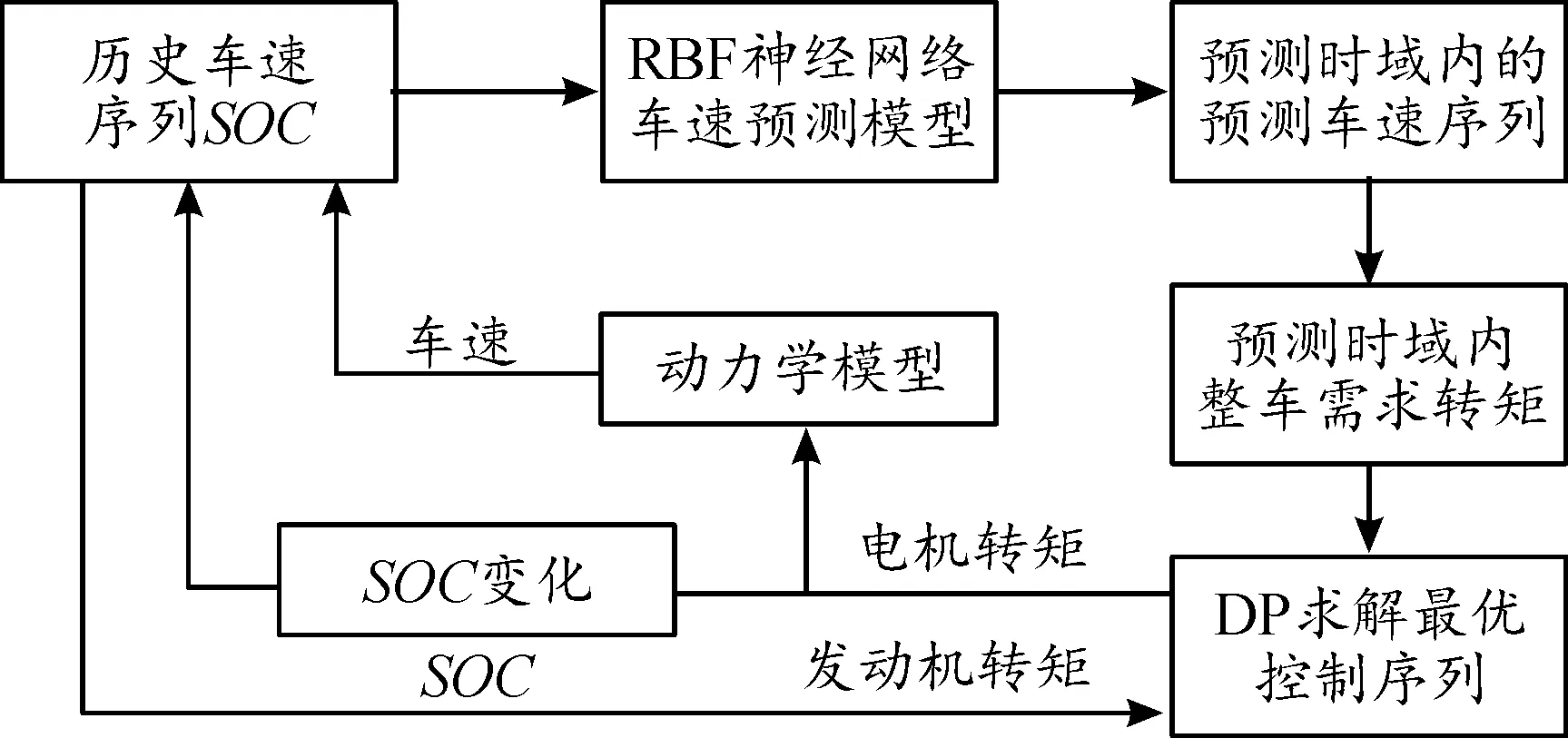
圖7 預測控制能量管理策略求解流程框圖

首先，在當前采樣時刻k，以過去p秒內的車速為輸入，通過上文所建立的RBF網絡車速預測模型預測未來的p秒的車速，并根據式(8)計算出預測時域內的整車需求轉矩；其次，采用動態規劃算法對預測時域內控制變量進行優化[13]，得到控制變量的最優控制序列；然后，將最優控制序列的第一個元素應用到模型中，并進入下一采樣時刻，重復預測和求解步驟[14]，直至仿真結束。

(8)

式中：Ff為滾動阻力；m為整車質量；f為滾動阻力系數；α為坡道角；Fw為空氣阻力；CD為空氣阻力系數；A為迎風面積；ua為車輪車速；Fj為加速阻力；δ為旋轉質量換算系數；Fi為坡度阻力；Tr為整車需求轉矩；r為車輪半徑；ig為變速器速比；i0為主減速器速比；ηT為傳動系統效率。

3.2 動態規劃方法

選取電池SOC作為狀態變量，系統狀態轉移方程為：

(9)

發動機和電機轉矩與整車需求轉矩關系如下：

Tr(k)=Tm(k)+Te(k)

(10)

式中：SOC(k+1)為k+1時刻電池SOC；SOC(k)為k時刻電池SOC；C為電池總容量；Tr(k)為k時刻整車需求轉矩；Te(k)為k時刻發動機轉矩；Tm(k)為k時刻電機轉矩。由式(10)可知，只要確定一個動力源的轉矩即可求得另一個動力源的轉矩，本文中選取發動機的輸出轉矩為系統控制變量。

狀態變量和控制變量如式(11)所示：

(11)

選取燃油消耗量最小作為能量管理策略的優化目標，最優值函數如式(12)：

(12)

式中：fk(SOC(k))為最優值函數，即預測時域內工況的燃油消耗最小值；n為預測時域離散后的階段數；Vk(SOC(k)，Te(k))為k階段的燃油消耗量。

同時，SOC、發動機和電機轉矩、轉速需要滿足以下約束條件：

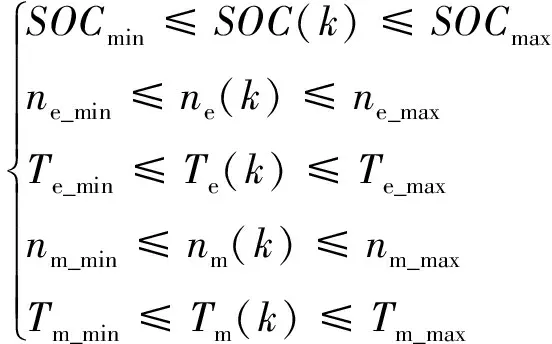
(13)

式中：SOCmin為動力電池SOC最小值；SOCmax為動力電池SOC最大值；ne_min為發動機最小轉速；ne_max為發動機最大轉速；Te_min為發動機最小轉矩；Te_max為發動機最大轉矩；nm_min為電機最小轉速；nm_max為電機最大轉速；Tm_min為電機最小轉矩；Tm_max為電機最大轉矩。

4 系統建模及仿真分析

4.1 發動機模型

發動機油耗率表征為發動機轉速ne和轉矩Te的函數，圖8為發動機的油耗特性圖。

(14)

圖8 發動機油耗特性

4.2 電機模型

電機效率為電機轉速nm和轉矩Tm的函數，電機效率的特性曲線如圖9所示。

ηm=f(nm，Tm)

(15)

式中：ηm為電機效率。當電機轉矩為正時，電機處于驅動狀態；電機轉矩為負時，電機處于發電狀態。2種狀態下的電機功率計算如下：

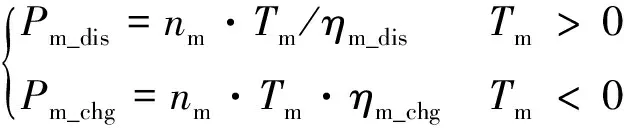
(16)

式中：Pm_dis和Pm_chg分別為電機驅動、發電狀態下的功率；ηm_dis和ηm_chg分別為電機驅動、發電狀態下的效率。

圖9 電機效率特性

4.3 電池模型

電池開路電壓和充放、電電阻的關系如圖10所示。將電池模型簡化為等效內阻模型，見圖11，表達式如下：

(17)

(18)

(19)

式中：I為電池電流，Voc為電池開路電壓；R為電池等效內阻；Pb為電池充、放電功率；ηb為電池效率；SOCt為t時刻電池荷電狀態；SOC0為初始時刻電池荷電狀態。

圖10 單體電池開路電壓和內阻與SOC的關系

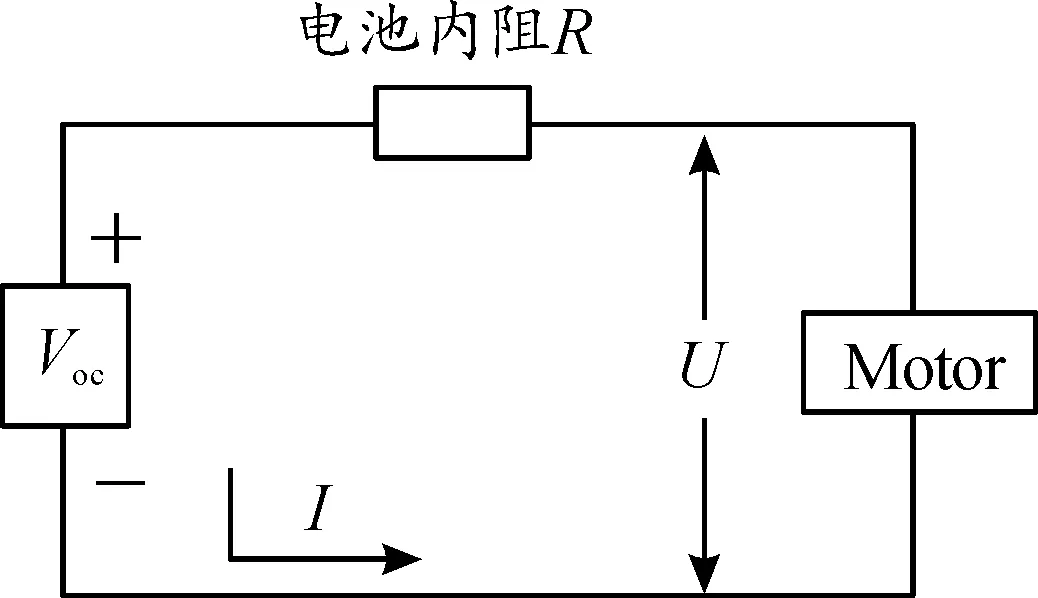
圖11 電池等效內阻模型

4.4 仿真分析

為驗證所提出的基于模型預測控制的能量管理策略性能，在8個NEDC工況下，分別對本文所提出的預測控制策略、基于規則策略中的CD-CS策略和DP策略進行仿真比較。設定電池的初始SOC為0.9，最小值為0.35。預測控制的預測時域為10 s，采樣間隔時間為1 s。3種策略的發動機和電機工作點分布、SOC變化和發動機的油耗分別如圖12～15所示。

圖12 發動機工作點分布

圖13 電機工作點分布

圖14 SOC變化曲線

圖15 發動機油耗曲線

圖12、13為3種策略下發動機和電機的工作點分布。可以看出，MPC和DP策略的發動機工作點主要集中在最優工作曲線附近，較之于CD-CS策略的工作點可更少地落在低速低轉矩區域內。圖13中：DP和MPC策略的電機工作點主要集中在轉速1 000～3 000 r/min、轉矩±100 N·m，且MPC策略的電機工作點更為集中，CD-CS策略的工作點更為分散，主要是在CD階段電機提供所有驅動轉矩，其工作點更為廣泛。

由圖14可見：CD-CS策略的SOC先快速下降，然后再在設定的門限值上下波動，其軌跡明顯分消耗和維持2個階段，MPC的策略SOC近似線性變化，DP策略SOC和MPC的趨勢一致，但DP策略的SOC存在波動。3種策略的SOC最終都維持在0.35左右，說明3種策略都能在滿足整車需求轉矩的條件下，維持住電池的SOC。由圖15可見：對于CD-CS策略，在CD階段油耗呈平穩增長，而在CS階段油耗則快速增長；DP與MPC的油耗隨行程的增加而增加。

表3為3種策略的油耗仿真結果。由表3可知：全局尋優的DP策略有最小油耗，CD-CS策略的油耗最大；MPC策略相較于DP策略，其油耗增加了9.4%，但與CD-CS策略相比，MPC策略的油耗降低了13.8%。

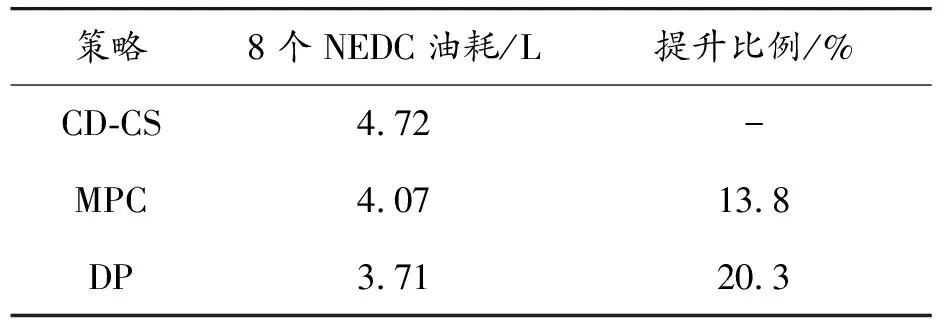
表3 不同策略下燃油消耗量

5 結論

1) 應用BP和RBF神經網絡，建立車速預測模型，針對 NEDC工況進行了車速預測。預測結果表明，RBF神經網絡車速預測精度優于BP神經網絡。

2) 基于RBF神經網絡車速預測模型得到了預測型能量管理策略，將SOC和發動機轉矩作為狀態變量和控制變量，得到了基于動態規劃算法的能量管理策略。

在8個NEDC工況下進行仿真對比。結果表明：MPC策略油耗相較于DP策略增加了9.4%，與CD-CS策略相比，油耗降低了13.8%。