基于二進制編碼多導頻搜索的導頻設計
黃海燕,朱俊杰,鄭志安,何明芳,劉健健
(中南林業科技大學 計算機與信息工程學院,長沙 410004)
0 引 言
正交頻分復用 (Orthogonal Frequency Division Multiplexing ,OFDM) 技術作為無線通信的核心技術,能夠有效抵抗無線通信傳輸的多徑效應。而在OFDM系統中,信道估計十分必要,傳統算法常常使用最小均方誤差(Minimum Mean Square Error, MMSE)和最小二乘誤差(Least Square, LS)[1]作為信道估計算法,導頻開銷較大。近年來,壓縮感知(Compressive Sensing, CS)在信道估計中的應用考慮了信道的系統特性,不僅提高了系統性能,還降低了導頻開銷,提高了頻譜利用率。
CS理論中[2],測量矩陣的構造必須滿足有限等距性質(Restricted Isometry Property, RIP),但在應用中無法實現。而文獻[3-7]提出了利用信道數據MMSE和最小互相干性(Minimum Mutual Property,MIP)的測量矩陣設計方案,由于MIP易于實現,方便檢驗,故本文主要是利用MIP作為優化導頻的目標函數。雖然窮舉法可以找到最優導頻,但其占用大量內存且有較高的計算復雜度,不具有實用性。文獻[8]通過數學推導出滿足循環差分集(Cyclic Difference Set,CDS)導頻集的MIP最小,但并非所有的載波與導頻集都有CDS,因此文獻[6]提出了一種基于離散隨機逼近 (Discrete Stochastic Approximation, DSA) 算法來尋找導頻集,但當子載波數目較大時,搜索空間會增大;文獻[9]提出了一種具有內外循環的隨機順序搜索(Stochastic Sequential Search,SSS)方法,其通過內外循環迭代尋找最優導頻集合,但 SSS方法需要更多的計算復雜度和更長的時間,且子載波數量越大,時間復雜度呈指數增長;文獻[10]提出了基于遺傳算法的導頻設計算法,但該算法需要的交叉和變異概率需要不斷驗證,否則算法容易局部收斂;文獻[11]基于尾迭代串聯CDS的方法尋找導頻,但該方法找到的MIP并非最小。現有文獻[12-16]中的算法都是從全子載波中選擇導頻集,在實際應用中,并非所有的子載波都放置了數據,因此從實際出發,本文考慮有限帶寬范圍的導頻集合。
本文提出了一種基于二進制編碼的多導頻并行搜索導頻優化算法,該算法將導頻集合進行了二進制編碼,利用MIP準則進行導頻更新。更新導頻首次采用多個導頻同時更新,增加了導頻組的多樣性,為下次迭代提供了更多可能性。實驗結果表明,該算法能找到較優的導頻集合,是可以提高信道估計性能的優化試驗模型。
1 系統模型
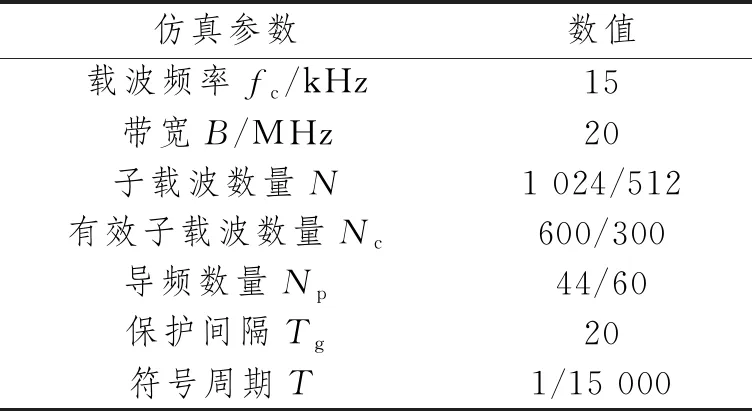
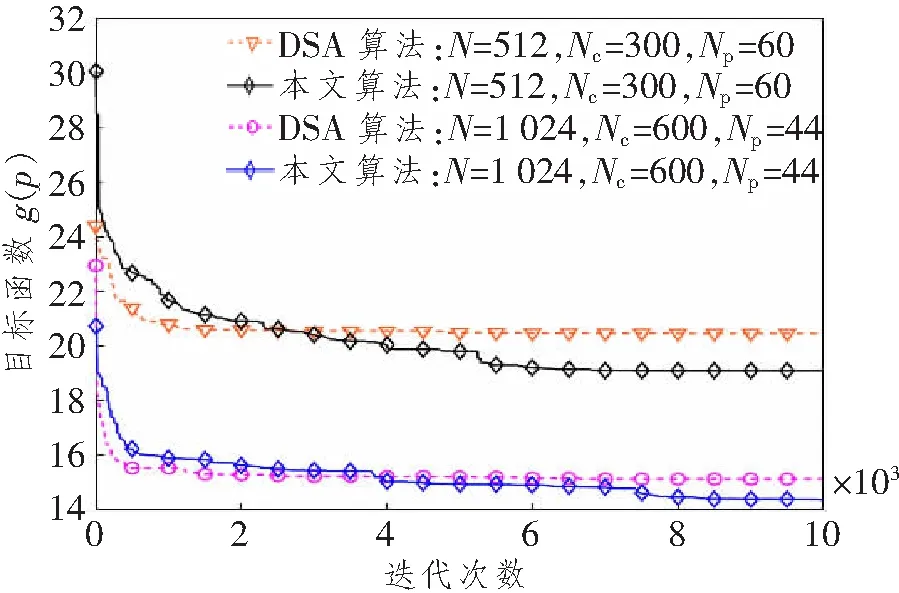
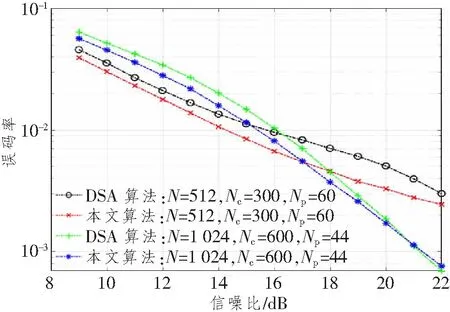
我們考慮N個子載波的OFDM系統,其中Nc和Np分別為有效子載波和導頻。在有效子載波范圍內,一組導頻P={p1,…,pNp}?Nc?(1 式中:k為虛數;τL為時延集合;T為OFDM符號長度。考慮到信道固有的系數信道沖擊響應,信道估計技術能夠利用較少的導頻得到準確的信道估計。本文利用測量矩陣的MIP作為選取導頻集合的目標函數,MIP為矩陣F任意兩列的最大內積,如下所示[10]: 式中,fm和fn分別為矩陣F第m與第n列的值。 本文沒有考慮到導頻符號的能量,所以式(3)可以寫成: 導頻優化的最終目的就是找到MIP。其目標函數為 則最優導頻位置popt可表示為 圖1 導頻排列示意圖 對導頻位置進行二進制編碼后,導頻優化的目標函數Q0變為 式中:s為所有導頻可能的搜索組合;p為每個OFDM符號的導頻組合。 對一個OFDM符號按式(7)進行二進制編碼,其中任意連續兩個及兩個以上的編碼統稱為編碼段。圖2所示為一個OFDM符號的二進制編碼示意圖。 圖2 一個OFDM符號的二進制編碼圖示 本文算法流程圖如圖3所示。 圖3 算法流程圖 算法的具體步驟如下: (1) 初始化; (2) 隨機編碼生成M組導頻集合: 式中:P為一個二進制矩陣;i為接下來的迭代次數。 (3) 將式(5)作為目標函數,計算式(9)矩陣每一行的MIP值,選擇具有較小MIP的K行,復制M/K次形成一個如式(9)初始尺寸規格的矩陣,其中M能被K整除,M/K的大小取決于想要的矩陣大小,本文一般取3~6之間。 (4) 更新導頻位置,導頻更新規則為 式中:Pi為一個OFDM符號的編碼位置,也就是導頻位置;updatelen和α分別為編碼更新長度和起點。找到更新起點并更新編碼段,然后更新導頻。圖4所示為對更新起點為α和編碼段長度為updatelen的導頻進行隨機編碼更新的規則示例圖,其準則是該編碼段導頻數量不變,只是隨機更新其導頻位置。 圖4 導頻更新的規則示例 然而,導頻更新有一些特殊的情況,可以總結如下:當更新起點正好是在無效子載波起點往前一個更新長度updatelen的任意一點時,則導頻更新可表示為 更新導頻只在式中對應的OFDM符號位置選中導頻,再將其更新替換為新的導頻組。 同理,當選中的編碼段正好與載波后半部分長度一致時,則導頻更新的原則為 即只在該更新編碼段開始尋找任意的編碼段,并將原始編碼段替換為該編碼段更新后的導頻位置,變成新的導頻更新組。 (5) 重復步驟(3),直到算法迭代次數結束,找到MIP的二進制編碼。 (6) 解碼找到導頻集合,算法結束。 為了驗證算法的有效性,在本節中使用所提算法和DSA[8]算法來尋找最優的確定性導頻模式,并且比較所提算法與現有方案DSA[8]算法的性能,實驗采用正交幅度調制(Quadrature Amplitude Modulation,QAM)。表1所示為OFDM系統的仿真參數。 表1 OFDM 系統的仿真參數 圖5所示為本文所提算法和DSA算法的MIP收斂速度曲線圖。我們給出了兩組對比圖,算法每次仿真都保證在相同的搜索空間中。由圖可知,無論子載波的數量為512還是1 024,本文所提算法都能夠比DSA算法收斂的更快,且能夠找到更小的MIP矩陣,說明本文所提算法性能較好。 圖5 不同算法的收斂比較 圖6所示為本文所提算法和DSA算法的誤碼率性能隨信噪比的變化曲線。由圖可知,當子載波數為512時,本文所提算法誤碼率性能明顯優于DSA算法。當子載波數為1 024時,本文所提算法在信噪比較小時一直優于DSA算法,而在信噪比較大時,本文所提算法與DSA算法的誤碼率幾乎相等。導頻的開銷越大,性能相對越差,該性能差異是由比較的子載波個數不同導致的。 圖6 本文算法與DSA算法的誤碼率比較 表2給出了本文所提算法和DSA算法在提出的無效子載波條件下找到的最小MIP導頻集合。由表可知,本文所提算法的g(p)值小于DSA算法,給出的導頻集合可方便讀者驗證導頻數據的真實性。 表2 DSA與本文所提算法的導頻集合 本文研究了有效子載波范圍內稀疏信道的導頻優化算法。與現有方法相比,本文將多個導頻進行并行搜索,而不是單一的迭代導頻,由此增加了導頻組合的多樣性。實驗結果表明,與現有方法相比,本文所提方法具有更小的MIP,且優化后的導頻模型具有更好的稀疏信道估計性能。然而,在有效載波選擇導頻的情況下,本文對MIP的下界還沒有理論驗證。
2 導頻圖樣設計算法
2.1 導頻的二進制編碼
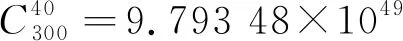
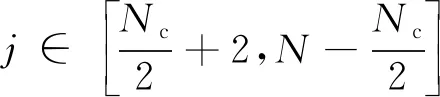

2.2 編碼段

2.3 算法步驟


3 系統仿真

4 結束語

