淺談初中數學“讀、思、說”三位一體學習法
李曉云

【摘要】本文首先提出數學成績中下的學生面臨的問題與解決問題的思路,然后對“讀、思、說”三位一體學習法進行解構與邏輯系統分析,從而獲得簡化、易操作的“讀、思、說”三位一體學習法的問題表,最后通過2個案例具體闡述該學習法在初中代數與幾何教學中的應用。
【關鍵詞】數學閱讀;數學思考;說數學;學習法
一、問題的提出與解決的思路
數學成績中下的學生普遍存在的問題:數學閱讀障礙;采用被動的學習方式,缺乏自主思考;欠缺向別人問數學問題的方法,不會用數學語言與老師、同學進行表達交流。為了解決上述問題,筆者先做了三份問卷調查,分別了解初中生在數學閱讀、數學思考與數學表達三方面各自的情況,分析其產生的原因,再通過文獻搜索和教學實踐,把“讀、思、說”三位一體進行系統的研究,探索出一種新的學習方法。
二、“讀、思、說”三位一體學習法的解構
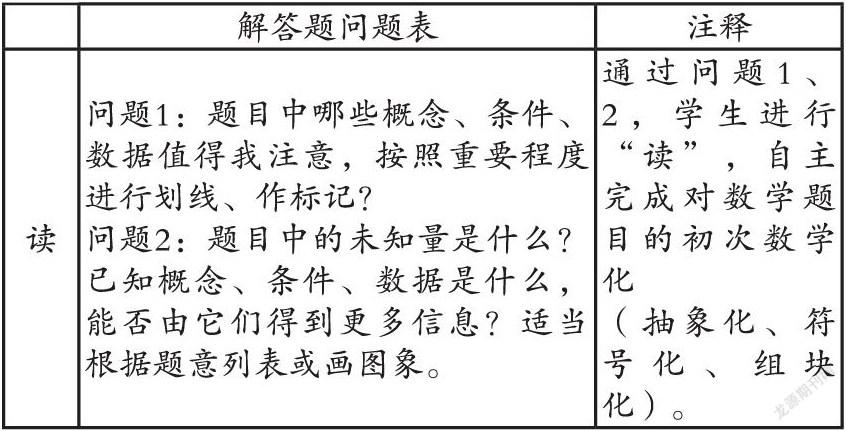
“讀”即數學閱讀,本文的數學閱讀材料特指數學題目。“思”即數學思考,本文的“思”分為進行數學閱讀的“思”與解決數學問題的“思”兩個層次。“說”是指“說數學”,即數學表達,用數學語言把題目涉及的知識點,解題策略,思想方法,思路探索過程等表達給自已、同學、教師聽。
“讀、思、說”三者相互聯系、相互制約。只有充分的“讀”,才能深入開展“思”;“讀”的過程中,必須帶著“思”進行;“讀與思”是“說”之本,沒有充分的“讀與思”,是“說”不出實質的東西;“讀與思”需要通過“說”來外顯,與外界進行信息交換,同時“說”能促進“讀與思”的深化。
(一)用簡化、易操作的問題表落實
自我提問的策略可以讓學生更自然地習得“讀、思、說”三位一體的學習法,同時提升他們的元認知水平。
三、“讀、思、說”三位一體學習法的應用案例
“讀、思、說”三位一體學習法采取問題串的形式開展,初期由教師引導提問,但目標是讓學生內化所有問題串的提問內容與方法,最終達到自問自答,形成自身一套良好的數學學習方法。
以其在代數中的應用為例:
某工程隊修建一條長1200m的道路,采用新的施工方式,工效提升了50%,結果提前4天完成任務.
(1)求這個工程隊原計劃每天修道路多少米?
(2)在這項工程中,如果要求工程隊提前2天完成任務,那么實際平均每天修建道路的工效比原計劃增加百分之幾?
(下面是學生自問自答解決題目的第1個問題,自我提問的問題詳見上述解答題問題表)
回答問題1:題中畫線的地方就是我要注意的,畫兩橫的是要特別注意的。
回答問題2:未知量是原計劃每天修道路的米數,即原計劃工效。已知數據是道路長1200m,條件是工效提升了50%和提前4天完成。已知概念是工作總量、工作效率(工效)與工作時間。我可以畫成表格梳理信息點,發現原計劃的工作時間也是未知量。
(數學閱讀到這里已經完成的使命,接下來是進行數學思考的相應自我提問。)
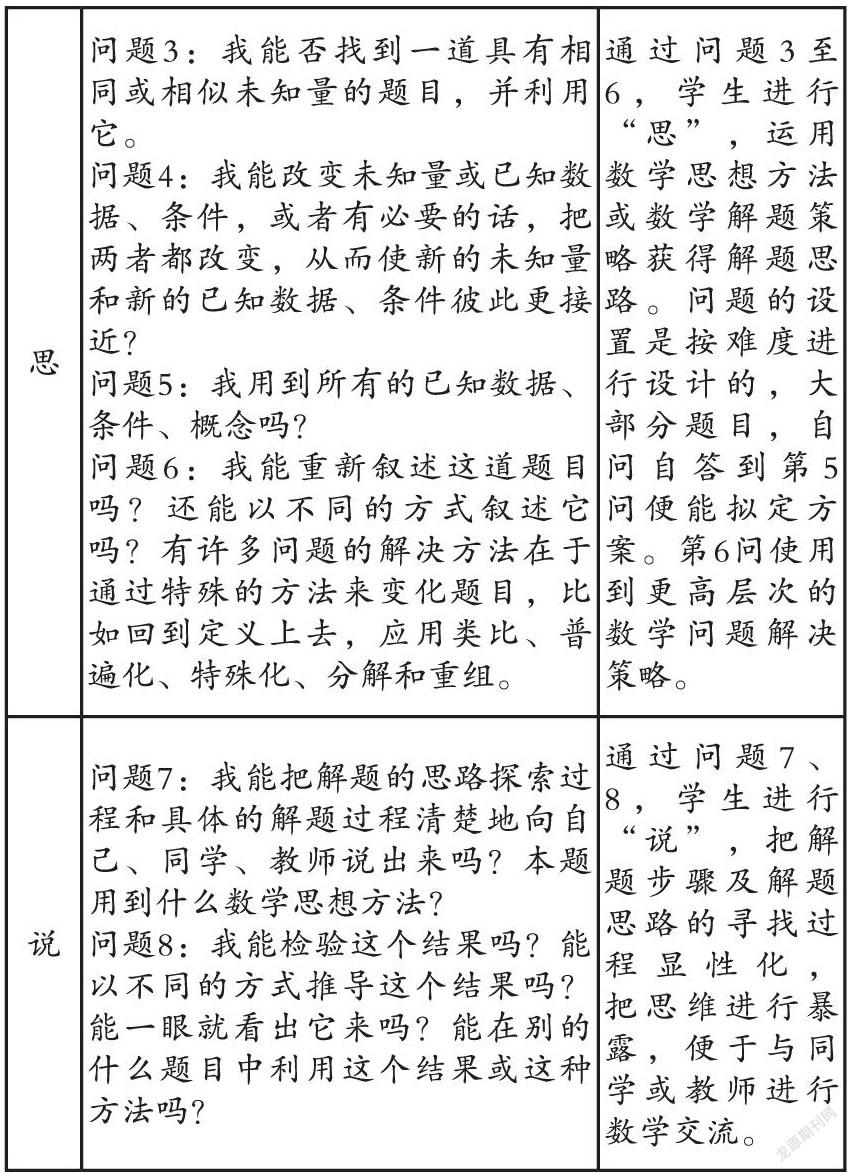
回答問題3:我以前做過求相同未知量的題目,但現在工作效率與工作時間都不知道,無法直接利用它們。可以用工式得到方程組xy=1200,1.5x(y-4)=1200,但是2次的二元方程組,可能可以解,但我以前沒試解過。
回答問題4:我把原計劃工作效率當作已知的數據,則原計劃的工作時間為? ? ? ? ? ,同理可得實際工作時間為? ? ? ? ? ? ? ? 。當然我也可以把工作時間看成已知,那可能是另外一種做法。
回答問題5:在第4問的前提下,我還有一個條件沒用上,那就是提前4天完成,即原計劃工作時間=實際工作時間+4。
(由于解題思路已經找到,所以數學思考的自我提問結束,不必要提問第6個問題)
回答問題7:思路探索過程就是回答前5問的過程,具體的解題過程如下(略)。本題用到了方程思想與代入消元的方法。
回答問題8:分式方程需要檢驗分母不為0,而且數據合理。這道題還有其它解法,前面的回答過程可以知道。現在我能一眼看出本題的解題思路。本題目第2個問需要用到第1問的結論。
四、結束語
由于本文的理論研究欠缺,所以對“讀、思、說”三位一體學習方法缺乏一個更系統更清晰的論述。問題表里的問題還不夠精煉、通俗化,如果能用學生熟悉的語言進行簡化表述,學生使用會更流暢。“讀、思、說”三位一體學習方法的應用案例,對“如何讀、如何思、如何說”闡述得不夠清晰。不管如何,本文的研究已經開啟了一扇能讓學生自主學習,把思維暴露、顯性化,用數學語言進行表達與交流的門。
【參考文獻】
[1] 歷小康.數學閱讀能力的培養研究[J].數學教育學報,2004,5.
[2] 何小亞.數學學與教的心理學(第二版)[M].廣州:華南理工大學出版社,2016.
[3] 斯萊文.教育心理學(第七版)[M].北京:人民郵政出版社,2010.
[4] 波利亞.怎樣解題[M].閻育蘇,譯.北京:科學出版社,1984.
(責任編輯:洪冬梅)

