P摻雜6H-SiC的第一性原理研究

黃思麗，謝 泉，張 琴

(貴州大學大數據與信息工程學院,新型光電子材料與技術研究所，貴陽 550025)

0 引 言

SiC是由Si和C組成的應用廣泛且經濟實用的半導體材料[1-2]，具有優異的物理化學特性和電學特性[3]，如禁帶寬、化學性質穩定、導熱系數大和漂移速度快等優點[4]。6H-SiC作為SiC中一種重要的多型體，具有結構最穩定、擊穿電子最強、電子遷移速度最快等特點而備受研究者關注[5]。

近幾年來，無論是在實驗或理論方面，6H-SiC材料的研究依然備受關注。很多學者對6H-SiC進行了摻雜研究，如楊昆等[6]使用物理氣相傳輸法制備出Ti摻雜6H-SiC襯底經過熱處理電阻率從小于105Ω·cm可增至1010～1011Ω·cm。Zhou等[7]采用V摻雜6H-SiC單晶襯底制備出了大功率光電開關，黃毅華等[8]計算了Al摻雜6H-SiC的磁性源于C原子的p軌道電子。Lin等[9]計算了N摻雜6H-SiC，得出本征和N摻雜6H-SiC均未表現出磁性，但 N和Si空位共摻表現出反鐵磁性。Nie等[10]研究了N、V摻雜6H-SiC晶體的載流子動力學和機理。張明軍等[11]研究了Al單獨摻雜6H-SiC 中的Si或C磁性微弱，共摻Si與C表現出強烈的磁性。臧源等[12]計算了Ge摻雜6H-SiC的電學與光學特性。鄒江等計算了La[13]、Ce[14]摻雜6H-SiC的電子結構與光學性質，王熠欣等[15]計算了Mn摻雜6H-SiC的第一性原理研究。以上Ge、La、Ce以及Mn摻雜可有效改善6H-SiC的電子結構與光學性質。Pinheiro等[16]對P摻雜6H-SiC進行了磁共振研究，但并沒有對P摻雜6H-SiC理論計算方面進行研究，且以往摻雜研究多集中于其磁性，對6H-SiC光學性質方面的理論研究較少，因此本文采用基于密度泛函理論的贗勢平面波法計算分析未摻雜與P替換Si、C以及間隙摻雜6H-SiC電子結構以及光學性質[17]。結果可為6H-SiC材料在光電領域的應用提供理論依據。

1 模型與方法

如圖1(a)所示穩定的6H-SiC為”ABCACB”型六方密堆積結構[18]，空間群為P63mc[19]，晶格參數a=b=0.309 5 nm，c=1.517 nm, 在晶胞的基礎上，向a與b基矢方向擴充一倍，得到2×2×1含有48個原子的超晶胞，并進行本次計算，體系中Si與C的原子數比例為1∶1。采用一個P原子替換一個Si原子，或替換一個C原子以及P間隙進行摻雜6H-SiC，三種摻雜方案模型圖如圖1所示。

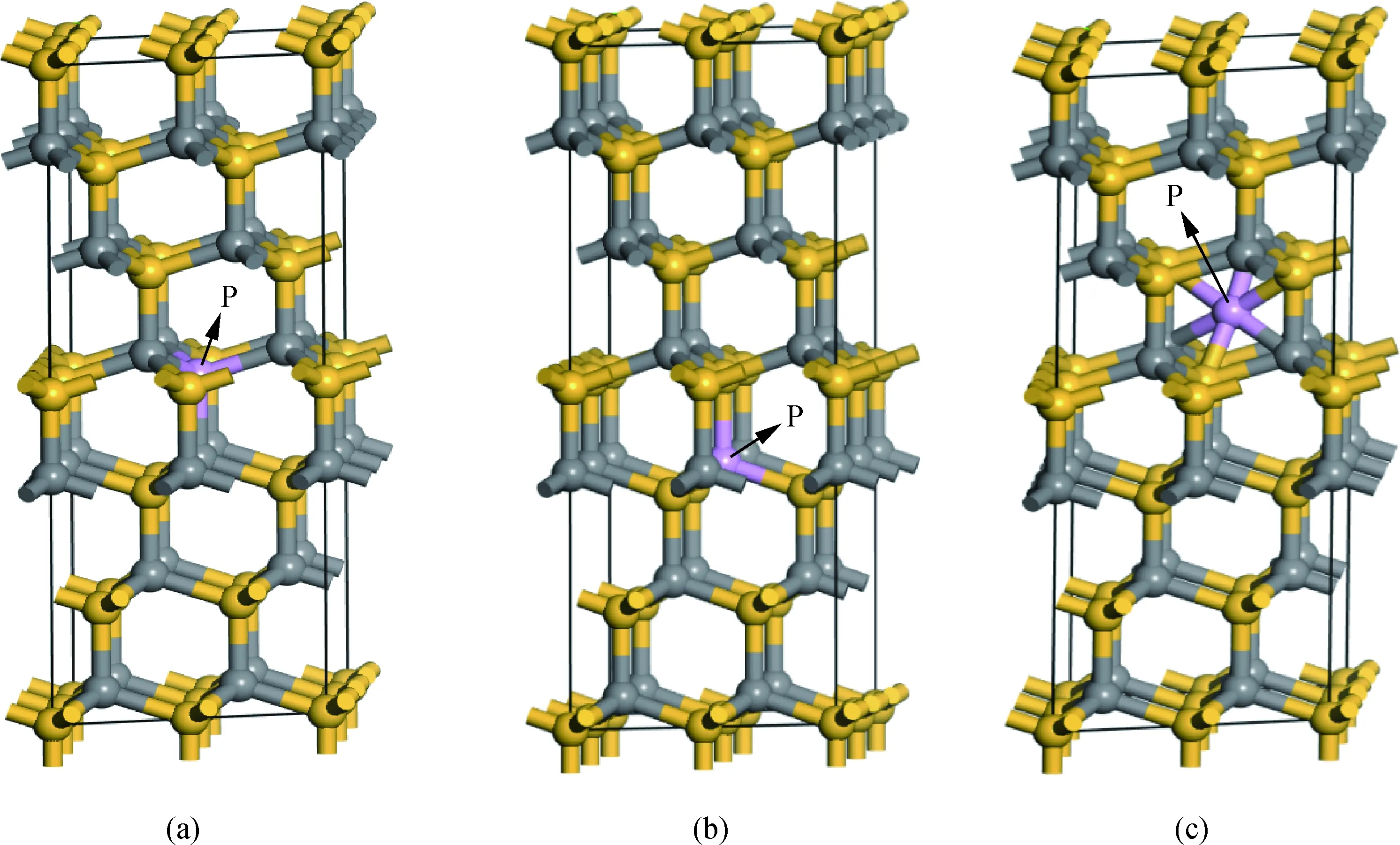
圖1 P摻雜6H-SiC的超晶胞模型：(a)P替換Si;(b)P替換C;(c)P間隙摻雜Fig.1 Supercell model of P-doped 6H-SiC: (a) P substituting Si; (b) P substituting C; (c) P interstitial doping

計算采用基于密度泛函理論(DFT)從頭計算方法，選用Materials Studio8.0中的CASTEP軟件包對未摻雜與P替換Si、C以及間隙摻雜6H-SiC的晶體進行結構優化[20]，經過收斂測試最終選定截斷能與網點設置分別為420 eV與3×3×1，收斂精度設置為5.0×10-4eV/atom,優化完成后再進行能帶結構、態密度以及光學性質的計算。

2 結果與討論

2.1 幾何結構

由表1可知未摻雜的6H-SiC優化所得結果與實驗結果接近，表明計算模型與計算方法是合理的。由于P與Si右鄰，它們的電子結構與原子半徑相似，因此P替換Si摻雜6H-SiC得到的晶格常數與晶胞體積變化不大。而P替換C摻雜由于P原子半徑(0.111 nm)大于C原子半徑(0.075 nm)，因此P替換C摻雜6H-SiC所得的晶格常數與晶胞體積變大。P間隙摻雜后體系中額外多了一個P原子，因此晶體的晶格常數與晶胞體積均膨脹變大。

表1 摻雜前后6H-SiC晶格常數、晶胞體積與摻雜形成能Table 1 6H-SiC lattice constant, unit cell volume and doping formation energy before and after doping

為了了解P替換Si、C以及P間隙摻雜6H-SiC的穩定性，進行了三者摻雜形成能的計算。形成能計算公式[21]如式(1)所示：

Eform=Etot(P∶6H-SiC)-Etot(6H-SiC)-nPμ(P)+nxμ(x)

(1)

式中：Etot(P∶6H-SiC)表示P摻雜6H-SiC的總能量；Etot(6H-SiC)表示未摻雜6H-SiC的總能量；nP表示摻雜P原子的個數；μ(P)表示摻雜原子P的化學勢；nx表示被替換原子Si或C的個數；μ(x)表示被替換原子Si或C的化學勢。當進行間隙摻雜形成能計算時，因P間隙摻雜時未有原子被替換，故公式(1)中nxμ(x)項不存在。若計算Eform結果值為負時，說明摻雜反應過程中釋放能量，反應較容易進行；若Eform值為正時，意味著發生反應過程中需要吸收能量，反應較難進行。Eform的值越小，證明其結構越穩定。從結果得出替換式摻雜比間隙式摻雜結構更穩定。

2.2 電子結構

2.2.1 能帶結構

從圖2(a)未摻雜6H-SiC原胞能帶圖看出，其價帶頂與導帶底位于不同位置，故為間接帶隙半導體。類似情況，圖2(b)超胞能帶圖中其價帶最大值與導帶最小值也位于不同點，因此超胞6H-SiC仍為間接帶隙，帶隙值為2.052 eV，與臧源等[12]計算結果一致，但比實驗值3.02 eV[22]稍小。這是由于密度泛函的估計誤差所引起，但對結果的總體趨勢分析無影響。

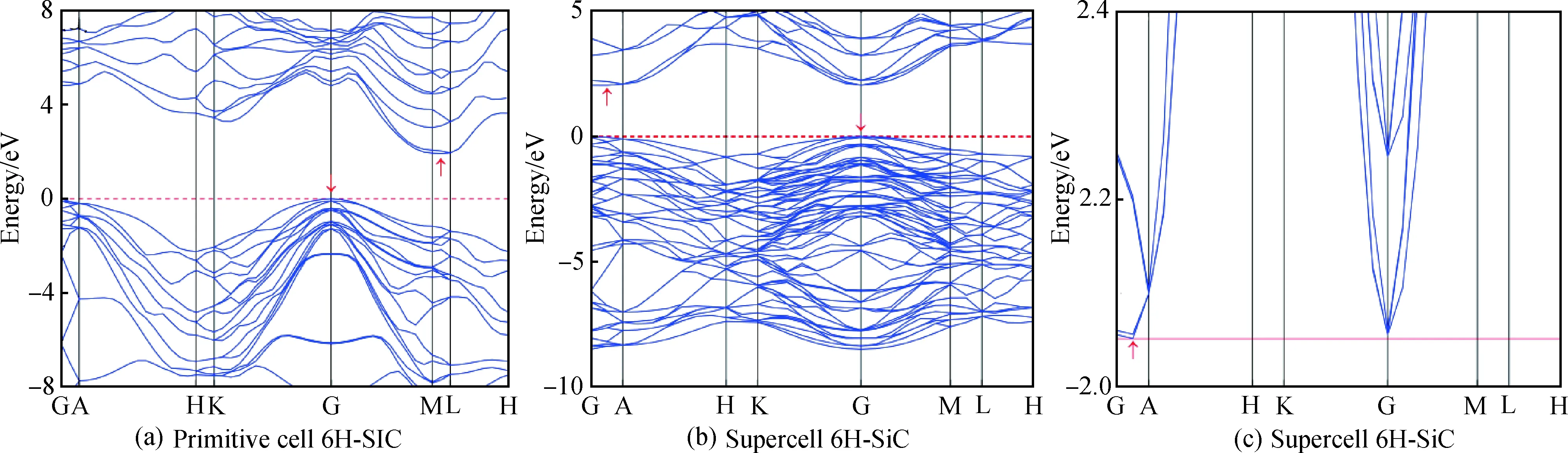
圖2 未摻雜6H-SiC的能帶圖:(a)原胞;(b)、(c)超胞Fig.2 Band diagram of intrinsic 6H-SiC: (a) primitive cell; (b), (c) supercell

圖3(a)與(b)為P替換Si、C摻雜的能帶圖。與未摻雜相比，在P摻入6H-SiC體系后，由于P比Si與C原子最外層多一個電子，故摻雜后可為導帶底附近提供大量電子，使得導帶與價帶均向低能級移動，同時價帶中能級數顯著增多，兩種替換摻雜使得費米能級移入導帶，顯然P替換Si、C摻雜6H-SiC導電類型為n型。圖3(c)為P間隙摻雜6H-SiC的能帶圖，與未摻雜的對比，間隙摻雜后價帶導帶均下移，但出現一條價帶向上移動并插入費米能級，形成施主能級并與費米能級重疊，部分施主雜質發生電離產生電子，費米能級下的受主能級提供空穴，即P的3p與C的2p。間隙摻雜中起主要作用的是費米能級下的受主能級，且空穴的產生大于電子的產生，間隙摻雜6H-SiC導電類型轉為p型。如表2所示，P替換Si、C摻雜后的帶隙值分別減小至1.787 eV和1.446 eV，間隙摻雜帶隙減小幅度最大，為0.075 eV。帶隙減小使得電子躍遷所消耗的能量減少，電子的躍遷加快，材料導電性增強。

表2 摻雜前后6H-SiC的帶隙變化Table 2 Band gap change of 6H-SiC before and after doping

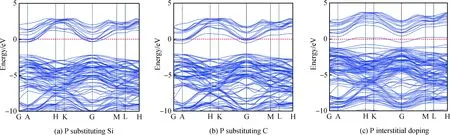
圖3 摻雜后6H-SiC的能帶圖:(a)P替換Si;(b)P替換C;(c)P間隙摻雜Fig.3 Energy band diagram of 6H-SiC after doping: (a) P substituting Si; (b) P substituting C; (c) P interstitial doping

2.2.2 態密度

圖4(a)為未摻雜6H-SiC的態密度圖，在價帶-15.6～-9.66 eV區域主要由Si 3s和3p以及C 2s態電子共同構成。在價帶-8.81～0 eV區域Si 3s和3p以及C 2p態電子貢獻最多，其中Si 3s和3p形成sp3軌道雜化，導帶部分由Si 的3p貢獻大部分電子，Si的3s以及C的2s、2p態電子貢獻小部分電子。其中C的2s與2p形成sp3雜化軌道。

圖4(b)為P替換Si摻雜的態密度圖，在-17.7 eV以及-10.8 eV處出現P 3s峰，局域性較強。P替換Si摻雜后使得P原子周圍的Si與C原子態密度發生變化，因Si和C與P重組成鍵，故部分態密度局域性減弱。P引入的 3p態電子易在導帶中形成游離電子(施主)；P 3p與Si 3p共同作用使得態密度向低能級偏移。由圖4(c) P替位C摻雜后的態密度圖看出，鄰近P的Si與C原子態密度發生變化較小，由于P的摻入在導帶附近提供3p電子，同樣由P 3p與Si 3p作用使得態密度整體向低能級偏移。圖4(d)為P間隙摻雜態密度圖，P間隙摻雜對周圍的Si與C原子影響比較大，由圖看出在-16.4 eV處出現了C的2s峰與P 3s峰，價帶部分Si 3p與C 2p態密度明顯下降且向費米能級移動，P 3p分裂為兩部分，分布在價帶頂與導帶底附近，費米能級附近態密度顯著增強，產生了與費米能級重合的施主能級，故而影響各電子態之間的躍遷。

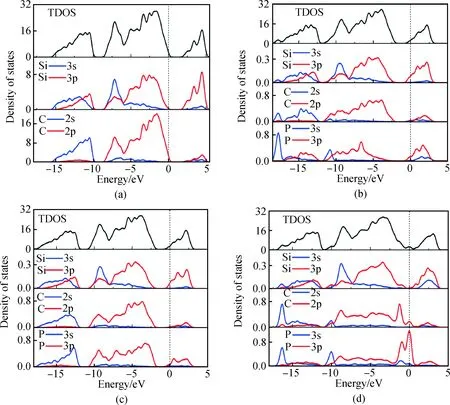
圖4 摻雜前后6H-SiC的態密度:(a)未摻雜；(b)P替換Si；(c)P替換C；(d)P間隙摻雜Fig.4 Density of states diagram of 6H-SiC: (a) intrinsic (b) P substituting Si (c) P substituting C (d) P interstitial doping

2.3 光學性質

2.3.1 復介電函數

圖5為摻雜前后6H-SiC的介電函數實部ε1(a)與虛部ε2(b)隨入射光子能量的變化而不斷變化的關系圖，由圖5(a)得出未摻雜6H-SiC在光子能量零點的介電函數ε1值為5.38，隨后不斷增大在5.3 eV處取得峰值12.1；P替換Si摻雜在能量零點的介電函數ε1值為6.6，在5.4 eV處取得峰值12，峰值變化較小；P替換C在能量零點的介電函數ε1值為7.32，在5.2 eV處取得峰值11.8；P間隙摻雜在光子能量零點的介電函數ε1值為6.7，峰值下降較明顯，在5.1 eV處取得峰值10.8。通過摻雜介電函數ε1在零點的值明顯增大。從5(b)得出未摻雜的6H-SiC在光子能為6.71 eV處取得介電函數峰值15.7，這歸因于價帶頂C 2p向導帶低Si 3p電子躍遷所致。引入雜質P后強峰稍有下降且偏移，偏移是由P摻入后提供電子，游離電子極化引起，峰值變化是由價帶頂C 2p向導帶低Si 3p電子躍遷以及C 2p與Si 3p到費米能級P 3p電子躍遷所致[23]。摻雜后6H-SiC的介電函數虛部在低能區顯著強于未摻雜的。摻雜后實部與虛部得到大幅度提升，結果表明摻雜對材料的光學參數影響較大。

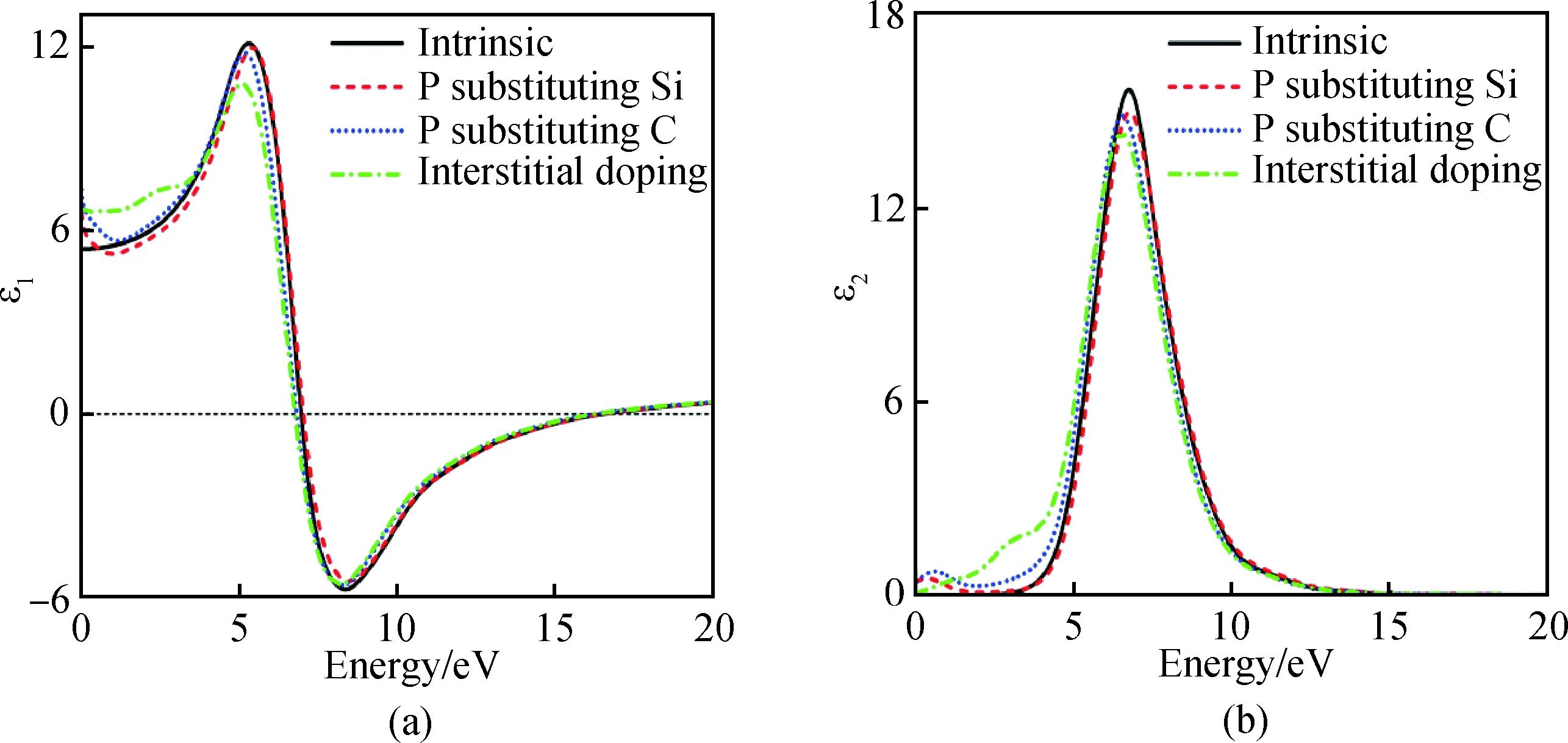
圖5 摻雜前后6H-SiC介電函數實部ε1(a)與虛部ε2(b)Fig.5 Real part ε1(a) and imaginary part ε2(b) of the 6H-SiC dielectric function before and after doping

2.3.2 吸收光譜與反射譜

圖6為摻雜前后6H-SiC的吸收光譜隨能量變化的關系圖，未摻雜的6H-SiC在能量小于2.4 eV以下不吸收光子，隨著光子能量的增大在8.25 eV處取得最大吸收系數3.61×105cm-1，之后隨著光子能量增加逐漸減小直至0。P替換Si、C與P間隙摻雜后均使得6H-SiC在小于2.4 eV以下吸收光子。P替換Si摻雜吸收峰與未摻雜吸收峰幾乎重合；P替換C摻雜與P間隙摻雜吸收峰值略有下降。摻雜后在大于2.4 eV以上與未摻雜的吸收光譜變化趨勢相似。

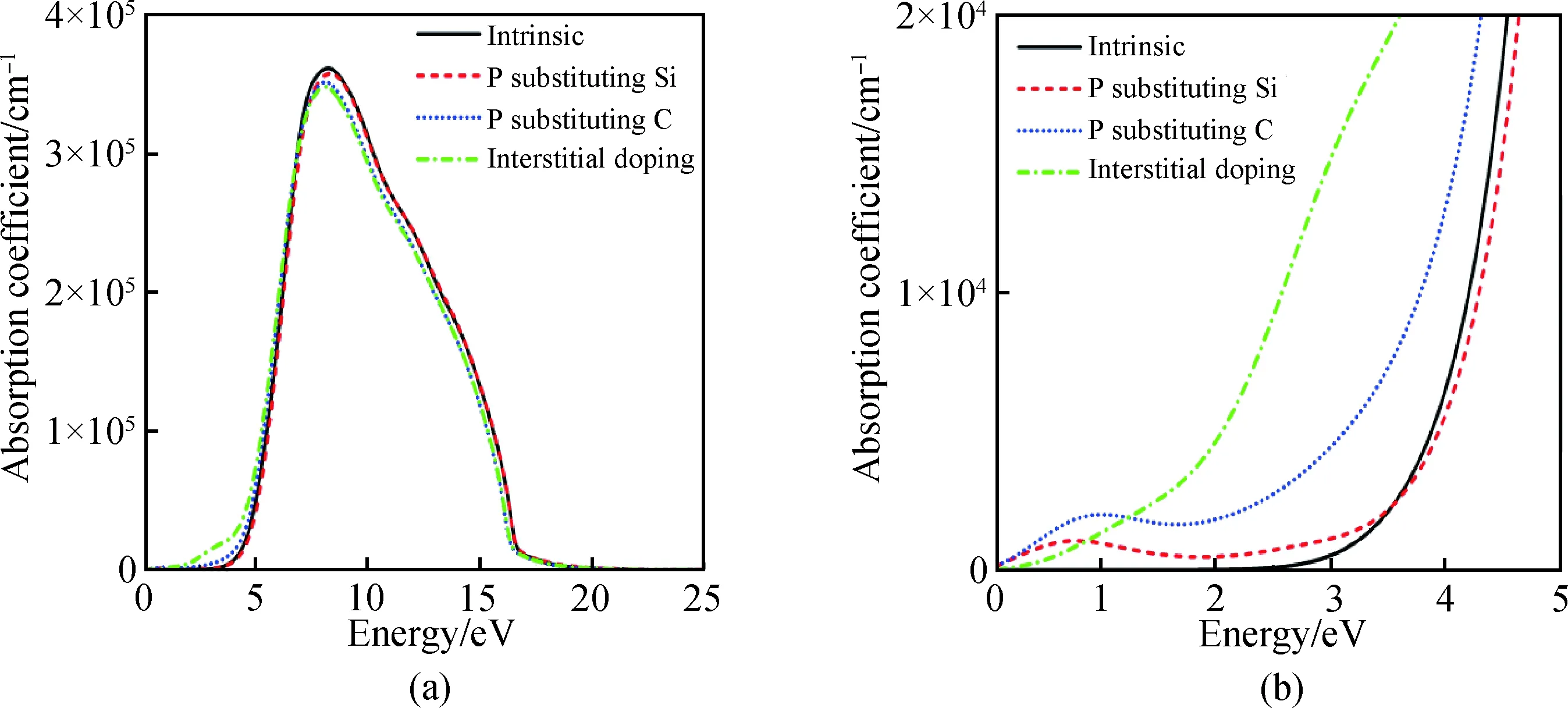
圖6 摻雜前后6H-SiC的吸收光譜Fig.6 Absorption spectra of 6H-SiC before and after doping

圖7(a)為摻雜前后6H-SiC的反射譜隨能量增大而不斷變化的關系圖，摻雜前后6H-SiC的反射譜圖在可見光與紫外光區變化不大，未摻雜的6H-SiC在15 eV處取得最大值，摻雜后的6H-SiC反射譜峰值略有減小。P替換Si、C以及P間隙摻雜6H-SiC反射譜出現紅移現象，P間隙摻雜效果最佳。

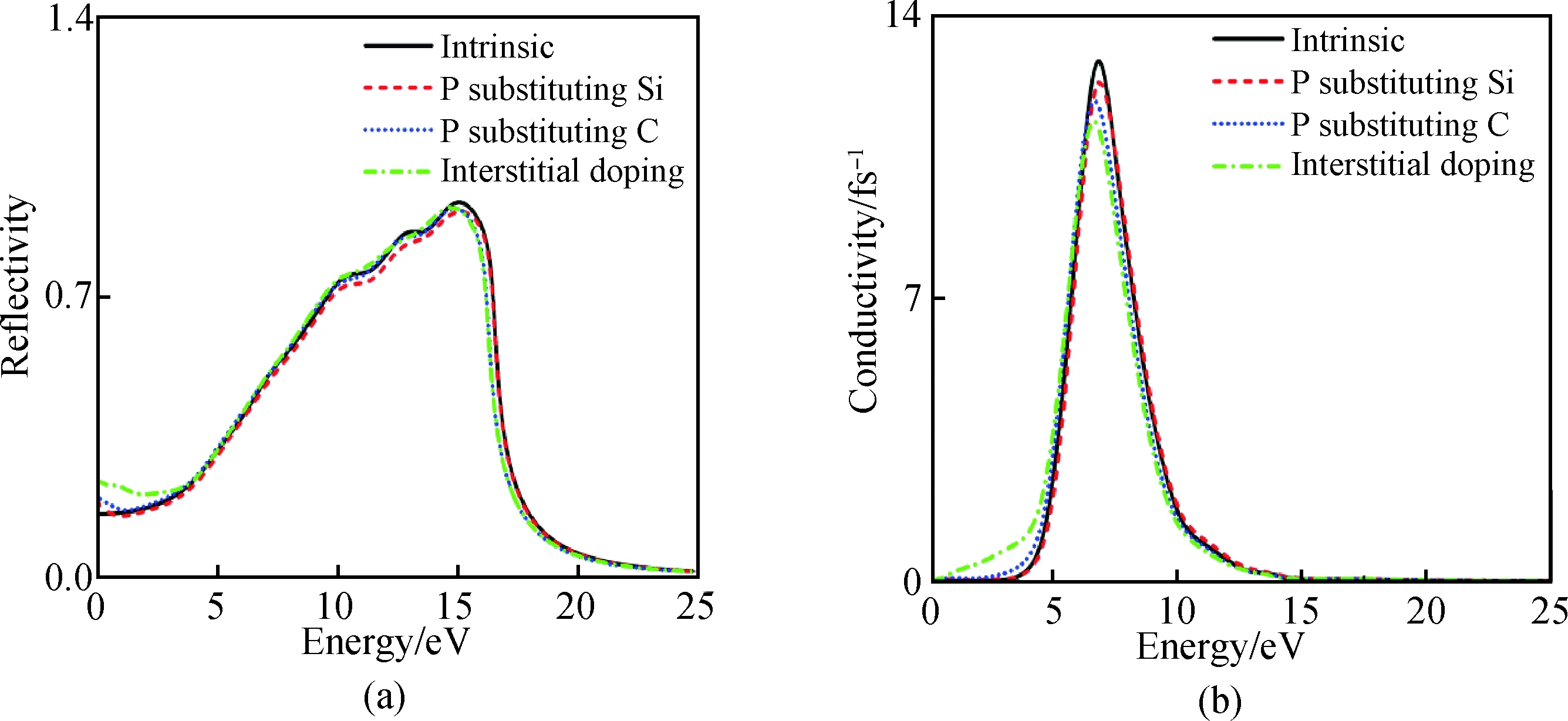
圖7 摻雜前后6H-SiC的反射譜(a)與光電導率實部(b)Fig.7 Reflectance spectra (a) and real part of photoconductivity (b) of 6H-SiC before and after doping

2.3.3 光電導率

圖7(b)為摻雜前后6H-SiC的光電導率實部與光子能量的關系變化圖。未摻雜的6H-SiC在能量小于2.2 eV以下光電導率為0，在2.2 eV以上隨著光子能量的增加光電導率單調遞增，在6.85 eV光子能處取得光電導率最大值12.9 fs-1，達到峰值后隨著光子能量增大光電導率單調遞減。P替換Si、C以及P間隙摻雜后光電導率峰值有所下降，在低能區發生紅移現象，在小于2.2 eV以下光電導率增強，其中間隙摻雜效果較明顯。摻雜前后整體趨勢在高能區變化不大。

3 結 論

基于密度泛函理論的贗勢平面波法，計算并分析了未摻雜以及P替換Si、C以及P間隙摻雜6H-SiC的電子結構與光學性質，結果如下：

(1)未摻雜的6H-SiC是帶隙為2.052 eV的間接帶隙半導體，價帶主要由Si 3s、3p與C 2p態電子共同作用形成，導帶占主導的是Si 3p態電子，P替換Si、C摻雜帶隙減小，分別為1.787 eV和1.446 eV；態密度向低能級偏移；費米能級插入導帶，P替換Si、C摻雜呈n型摻雜。P間隙摻雜6H-SiC后電子結構變化最大，能帶整體向下移動但部分價帶向導帶移動并跨入導帶，帶隙減小幅度較大為0.075 eV，P間隙摻雜呈p型摻雜。

(2) 未摻雜的6H-SiC在0 eV處的介電函數ε1值為5.38，P替換Si、C以及間隙摻雜6H-SiC在0 eV處的介電函數ε1分別為6.6、7.32和6.7，摻雜使得ε1顯著增大。P替換Si、C以及間隙摻雜6H-SiC后ε2峰值有所下降，在低能區發生紅移。未摻雜6H-SiC在2.4 eV以下不吸收光子，且在2.2 eV以下光電導率為0，摻雜P后6H-SiC的吸收光譜在0～2.4 eV范圍吸收光子，光電導率在0～2.2 eV不為零，且反射譜在低能區均強于未摻雜。P替換Si、C以及間隙摻雜后6H-SiC在低能區的光學性能均強于未摻雜的，且P間隙摻雜在低能區的光學性能優于P替換摻雜，表明摻雜提高了6H-SiC對紅外波段的利用。此次計算結果可為6H-SiC在紅外光電領域提供有效理論依據。