基于離散元仿真中堆積角評定新方法
劉 珂 魏偉鋒,2*
(1、陜西理工大學機械工程學院,陜西 漢中 723000 2、陜西省工業自動化重點實驗室,陜西 漢中 723000)
散體顆粒廣泛存在于自然界中,可作為加工對象或相關裝備的承載介質[1],散體顆粒特性研究對采礦、冶金、食品、能源、化工及農業等領域的裝備開發具有重要意義[2]。堆積角是散體顆粒特性參數之一[3],是顆粒物篩分、輸送、存儲裝備開發的基礎參數之一。
傳統的堆積角通過堆積實驗法得到,方法1:人工用角度儀對堆積體的幾個截面進行測量和數據處理得到堆積角度,具有直觀簡便的特點;方法2:通過不同角度堆積照片,對圖像處理得到堆積角。其共同點在于:測量對象是三維實體,測量截面的選擇對測量結果具有一定的影響,無法全面利用堆積體的幾何信息。
離散元仿真軟件的發展為散體顆粒的研究提供了新途徑。相關研究表明:a.在離散元仿真中可以將不規則的物體用相對規則的物體近似代替[4];b.離散元模型的填充顆粒半徑越小仿真結果越接近真實值[5];c.動摩擦因數及靜摩擦因數等物料參數的設置對仿真的結果具有重要的影響[6]。
離散元模型參數通常難以通過試驗測的,為獲取離散元仿真參數,研究者需要進行相應的模型參數標定;離散元模型的表征參數,一般通過堆積試驗與仿真結果對比進行離散元模型表征參數標定;基于離散元堆積角測量目前主要通過兩種方法。方法1,直接采用仿真軟件中的角度測量工具人為繪制邊界,如文獻[7-10],該方法容易引起人為誤差;方法2,通過圖像處理得到堆積角,如文獻[11-14]在標定不同離散元模型參數時,先將堆積體轉化為圖片,然后對其二值化的邊界采用最小二乘法得到堆積角。以上處理方法的共同特點在于:以堆積體上的有限截面作為樣本,未能充分利用堆積體的三維輪廓信息,造成降維性原理誤差。
為充分利用離散元仿真結果的三維數據,來提高堆積角的計算精度和效率,本文以粳米為例,建立離散元模型,模擬粳米自然堆積過程,得到每粒粳米顆粒的質心坐標,采用一種處理方法,提取三維質心堆積體表面質心點集,將表面質心點集繞軸線旋轉至同一象限,進行線性擬合,獲得堆積角度。
1 堆積角離散元仿真
1.1 顆粒模型
假設粳米顆粒為橢球體,其長軸為6.2mm,短軸為2.8mm[15],通過三維制圖軟件繪制三維模型并保存,三維模型導入到離散元仿真軟件中,得到的顆粒模型輪廓如圖1 所示。

圖1 粳米離散元模型
1.2 顆粒模型堆積條件及邊界參數
在離散元仿真軟件中,需對鋼筒中填充顆粒數估算,按照公式(1)對其估算[16],便于設置顆粒生成數量,顆粒、無底鋼筒之間的邊界參數如表1 所示。

表1 接觸模型參數

式中,α 為填充體積分數,α 一般取值為0.56;Vs為無底鋼筒體積(mm3),N 為填充顆粒數量(個),VF為填充顆粒的體積(mm3)。
1.3 離散顆粒堆積仿真過程
將半徑為30mm,高為180mm 的鋼筒及200mm×200mm 的不銹鋼底面三維模型導入離散元仿真軟件中,鋼筒填充滿粳米顆粒,設置鋼筒以0.05m/s 的速度向上移動,當離散模型堆積形狀不再發生改變后仿真結束,粳米將在底面上形成一個近似的錐體,其過程如圖2 所示。改變顆粒的填充效果,重復上述過程,獲得一組堆積角仿真數據。
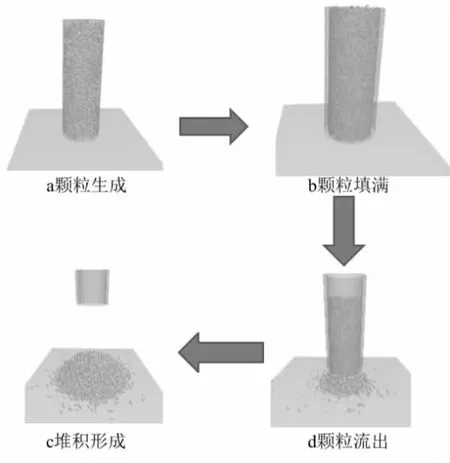
圖2 離散顆粒離散元仿真過程
2 堆積角評估方法
為了充分利用離散元仿真得到的堆積體三維信息,更為全面的反映堆積角,提出如下方法。
2.1 三維數據預處理
將離散元仿真結果的顆粒質心坐標導出,通過式(2)計算三維錐體質心坐標,由式(3)計算出,顆粒質心距三維錐體質心坐標距離,過質心坐標垂直于地面的直線為軸線。以軸線為三維堆積體坐標系Z 軸,形成堆積體坐標系,如圖3 所示。
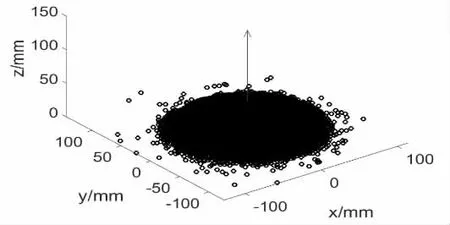
圖3 三維質心及軸線

式中,n 為顆粒數量(個),xc、yc、zc為三維錐體質心坐標(mm),xi、yi、zi為顆粒質心坐標(mm)。

式中,xr、yr為堆積角坐標系中顆粒相對橫坐標、縱坐標(mm)。
2.2 三維邊界法
在Matlab 中,首先將堆積時,散落在堆積體外部與堆積體底部顆粒剔除,再通過boundary 函數將堆積體邊界點集提取,并獲得邊界點集包絡圖,如圖4 所示。
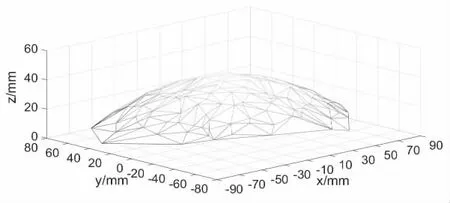
圖4 堆積體邊界
將堆積體邊界點集以堆積體坐標系Z 軸為旋轉中心,旋轉至同一象限,得到堆積體邊界點集圖,對其采用最小二乘法進行線性擬合得到擬合直線,擬合方程形式:y=-ax+b。擬合圖像如圖5 所示。
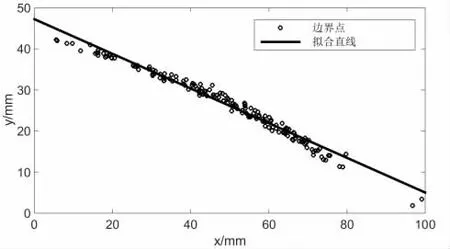
圖5 邊界點線性擬合
3 堆積角試驗對比
3.1 試驗準備
為保證試驗與離散元仿真軟件的條件相同,在試驗前對粳米進行挑選,對破損、形狀過小及過大的粳米進行剔除;無底鋼筒取半徑為30mm,高為180mm 的無底鋼筒,將篩選后粳米填滿無底鋼筒備用。
3.2 堆積試驗
將裝滿粳米的無底鋼筒,放置在不銹鋼試驗臺上,以0.05m/s 的提升速度在試驗臺上進行試驗,實際堆積體如圖6所示。

圖6 實際堆積體
3.3 結果與分析
對圖6 分四個方向進行圖像二值化處理,提取邊緣獲得輪廓線,進一步對輪廓線進行線性擬合,圖像處理結果如圖7 所示。計算堆積角公式(6),對計算結果取平均值,如表2所示。

表2 實際試驗堆積角
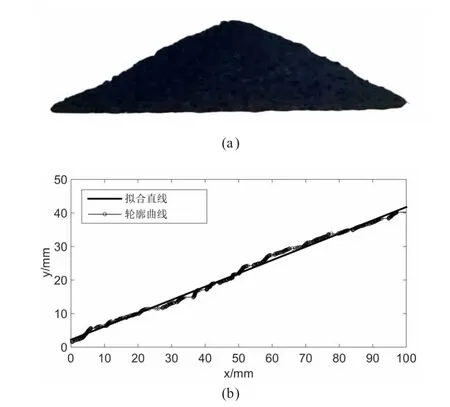
圖7 (a) 二值圖像(b) 線性擬合

式中,θp為實測堆積角(°),h 為粳米的堆積高度(mm),r 為粳米的堆積半徑(mm)。
以圖像法得到的實際堆積角為基準,使用公式(5)計算相對誤差,結果見表3。

表3 堆積角相對誤差

式中,δ 為相對誤差(%),θs為離散元仿真堆積角度(°),θp為實測堆積角(°)。
由表3 可知,本文測量方法與實際堆積實驗誤差為1.6%,在5%以內,是一種可靠的測量離散元仿真三維堆積角的新方法。
4 結論
4.1 基于離散元法仿真得到顆粒質心三維數據,通過計算堆積體質心,提出兩種邊界提取途徑,采用最小二乘法擬合邊界得到堆積角,充分利用堆積體邊界數據,實測堆積角與本文方法對比表明:相對誤差在5%以內,絕對誤差在±2°以內,表明本文提出通過三維堆積體質心邊界計算堆積角的可靠性。
4.2 本文提出的方法,克服了相位選擇和測量方向對堆積角計算和測量的影響,為離散元仿真評估堆積角提供了一種新的方法和思路。

