考慮載荷抑制的風電場分布式自動發電控制

姚 琦 胡 陽 柳 玉 羅智凌 綦 曉

考慮載荷抑制的風電場分布式自動發電控制

姚 琦1胡 陽2柳 玉3羅智凌2綦 曉1

（1. 暨南大學能源電力研究中心 珠海 519070 2. 華北電力大學控制與計算機工程學院 北京 102206 3. 國家電網華北電力調控分中心 北京 100053）

為了優化風電場進行自動發電控制時風電機組承受的疲勞載荷，提出一種風電機組控制模型并將其應用于風電場控制。建立了一種多入多出的風機控制模型，同時控制轉子轉速和槳距角。在此基礎上提出一種分布式控制框架的風電場控制系統，使得風電機組相互協調，并以改善疲勞特性為目標直接優化所有機組的轉子轉速和槳距角。仿真結果表明，該文提出的多入多出控制模型可實現對風電機組更加靈活有效的控制，結合風電場分布式控制框架，在完成自動發電控制（AGC）指令的前提下，風電機組疲勞載荷可以明顯降低。

自動發電控制 疲勞載荷 風電場 分布式控制

0 引言

隨著風電在電網中滲透率的不斷提高，其波動性和不可預測性給電力系統運行帶來了挑戰[1,2]。因此，許多國家的電力系統運營商在電網規范中都要求增加風力發電系統應具有可控性和快速響應能力[3]，提供符合要求的自動發電控制（Automatic Generation Control, AGC）[4]。

由于風電場不存在燃料消耗的成本，其運營成本主要來自設備損失等維護成本[5-6]，因此可將AGC問題與降低設備的疲勞水平相結合，以減少運行過程中設備損失帶來的成本[7]。現有研究提出多種表征風電機組疲勞的表征方式。文獻[7-8]通過構建成本函數來表征相關的運行成本。文獻[9-10]認為主軸轉矩和塔彎矩的標準差可用作風電機組的疲勞評估指標。文獻[11]指出，主軸轉矩和塔彎矩的標準差確實與機組的疲勞相關，但它們之間并非簡單的線性相關。一些研究人員采用了損傷等效載荷（Damage Equivalent Load, DEL）作為疲勞程度評估指標[12]。DEL在工程應用中得到了廣泛認可，但是DEL的計算過程復雜，難以用于在線優化過程。

通過機理模型分析可知，風電機組的主軸轉矩、塔彎矩及DEL等用于表征疲勞的參數均與機組轉子轉速和槳距角直接相關，而風電機組AGC的參數也是轉速和槳距角。因此在AGC控制過程中完成疲勞載荷抑制的研究思路是合乎物理規律的。針對風電機組的AGC，現有文獻中常用的控制方法包括轉子轉速控制[13-14]、槳距角控制[15]以及兩種控制的協調控制[16-17]。為了獲得更好的控制效果，文獻[18]提出同時激活槳距角和轉子轉速控制，槳距角控制用于在較大的時間尺度內跟蹤參考功率，轉子轉速用于在較小的時間尺度內精確調整功率。文獻[19]提出了一種類似的協調控制策略，認為應進一步使用轉子慣性減少槳距角伺服系統的動作，從而降低其疲勞程度。然而，現有文獻中，轉子轉速和槳距角的協調控制涉及多個控制器的協調，并不能通過單一控制器同時進行調整，槳距角需要在轉子轉速達到設定的閾值后才開始調整[20]，犧牲了槳距角調整的自由度。

由于風電場需要控制多個分布式單元機組，AGC過程除了需要考慮風電機組的控制，風電場層面的優化同樣重要[21]。在風電場層面，將電網運營商所需的有功功率合理地分配給風電機組是目前研究熱點[22-23]。文獻[9]對風電機組進行機組疲勞進行建模，然后采用模型預測控制（Model Predictive Control, MPC）實現考慮疲勞優化的機組功率分配。文獻[10]直接利用機理模型獲得有功功率與疲勞參數的偏導數關系，從而通過求解器獲得優化疲勞分布的風電機組功率指令。然而以上文獻中，研究人員采用的均為集中式控制方法，計算復雜度較高，且在風電機組層面均只采用了傳統的轉速和槳距角協調控制方法。文獻[24-25]中利用多智能體系統完成了風電場有功功率的分布式調度，機組之間通過相互通信即可完成調度指令的分配。文獻[6]提出一種基于分布式信息同步和估計的模型預測控制算法，用于對風電場有功功率和電壓同時進行優化。文獻[26]在等比例分配的策略下利用分布式的對偶梯度法完成了風電場有功功率的優化控制。然而，與文獻[9-10]中存在的問題相似，以上分布式控制算法也是在傳統風電機組協調控制模型的基礎上完成的，無法實現利用轉子轉速和槳距角的同時優化控制來改善機組疲勞特性。

針對以上研究現狀，本文提出一種可同時調整轉子轉速和槳距角的風電機組AGC模型。基于改進的機組控制框架，設計了一種基于交替方向乘子法（Alternating Direction Multiplier Method, ADMM）的分布式模型預測控制（Distributed Model Predictive Control, DMPC）框架來完成風電場功率控制，確保場內風電機組相互協調，針對AGC指令跟蹤和疲勞載荷抑制的目標完成轉子轉速和槳距角的同時控制。在疲勞載荷抑制目標方面，本文結合當前研究成果，以降低主軸轉矩和塔彎矩的波動性作為在線優化目標，以DEL為算法優化效果的評價指標。仿真實驗驗證了本文提出的風電機組控制模型的準確性和風電場分布式AGC算法的有效性。

1 風電機組建模

1.1 風電機組非線性模型

風電機組建模是相關控制器設計的基礎，對于進一步提高風電機組控制性能和風電場運行水平具有重要意義。風電機組的建模對象主要包括氣動系統、傳動系統、變槳伺服系統、電氣系統和控制系統。除控制系統外，對于其他子系統的建模已有大量文獻進行了研究。各個子系統之間的關聯如圖1所示。本文以NREL5MW風電機組模型為例，得到各個子系統的數學模型。

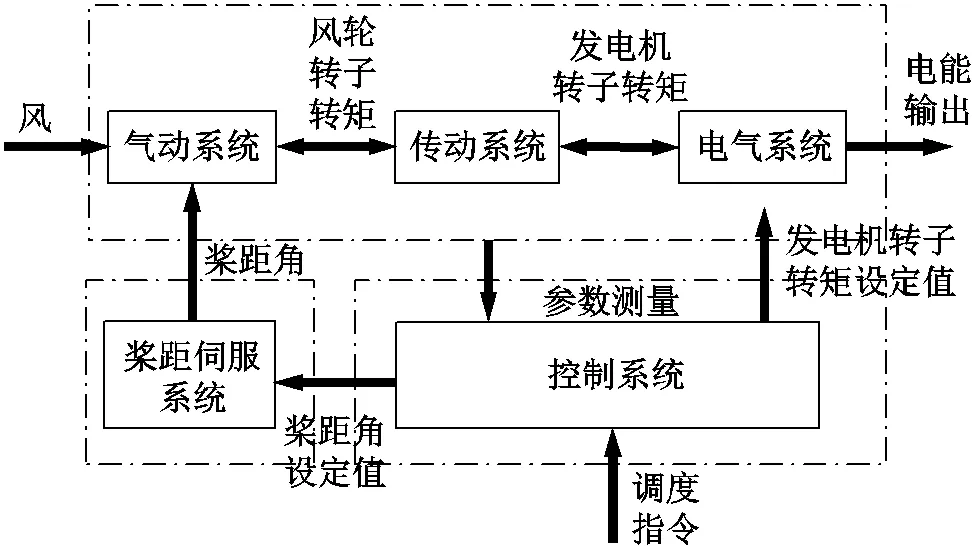
圖1 風電機組子系統的相互關聯

氣動系統

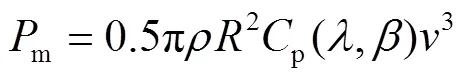
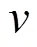
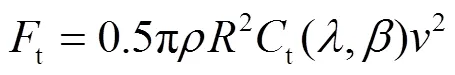
式中，t為風電機組承受的推力（N）；t為推力系數。

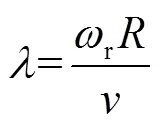
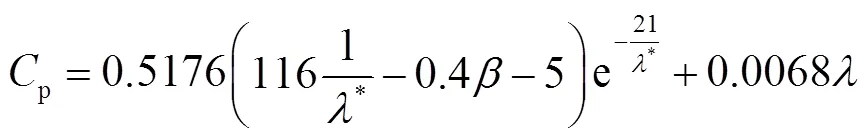
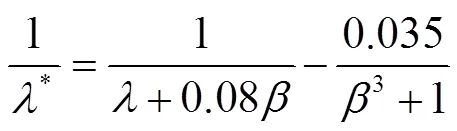
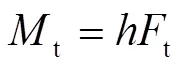
式中，為塔架高度；t為塔根彎矩（N·m）。

傳動系統

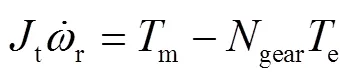
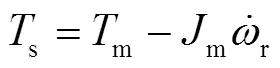
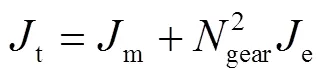
電氣系統

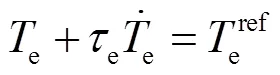
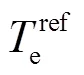
槳距伺服系統

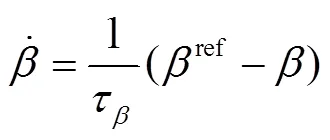
1.2 風電機組模型線性化

根據1.1節描述的數學模型，由于風電機組中存在高度的非線性特性，難以用于適合線性模型的先進控制算法。因此，本文通過小信號法[27]對上述模型進行線性化處理，得到線性化描述的風電機組模型。

氣動系統

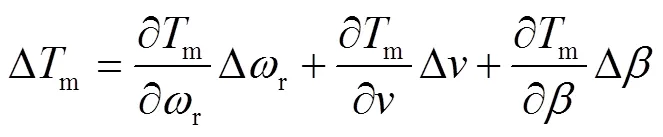
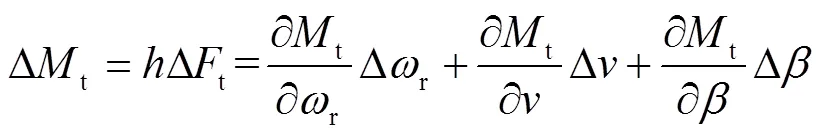
傳動系統

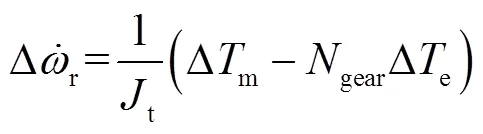
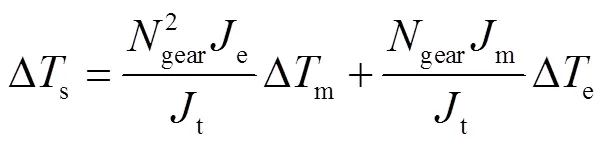
電氣系統

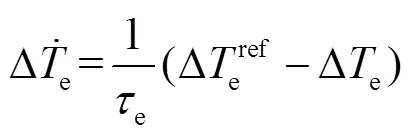
槳距伺服系統

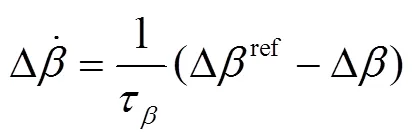
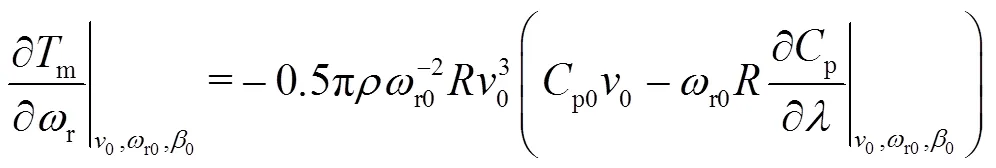
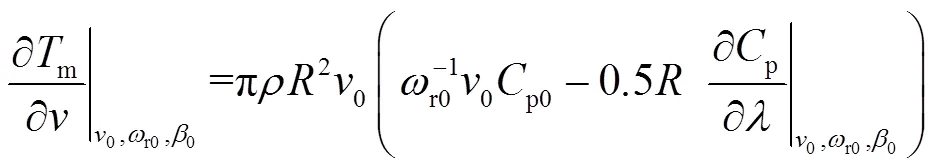
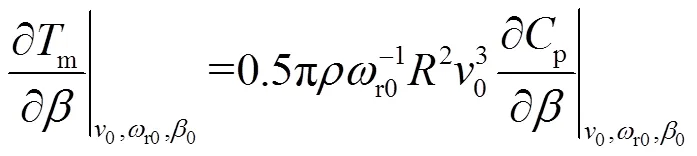
式中，下標為0代表線性化模型的初始工況點。

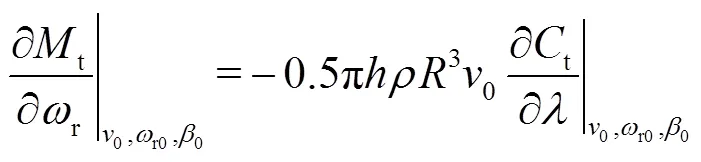
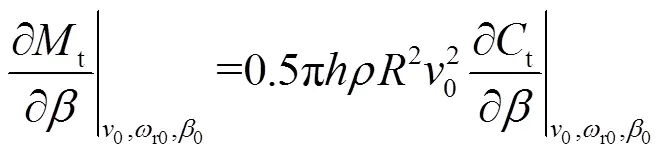
值得注意的是，根據式（4）和式（5），p具有高度非線性特性。為了進行線性化，本文根據p--曲線查表計算p的偏導數。假設工作點的p值為p0，則通過查表法可獲得其周圍的插值點，如圖2所示。

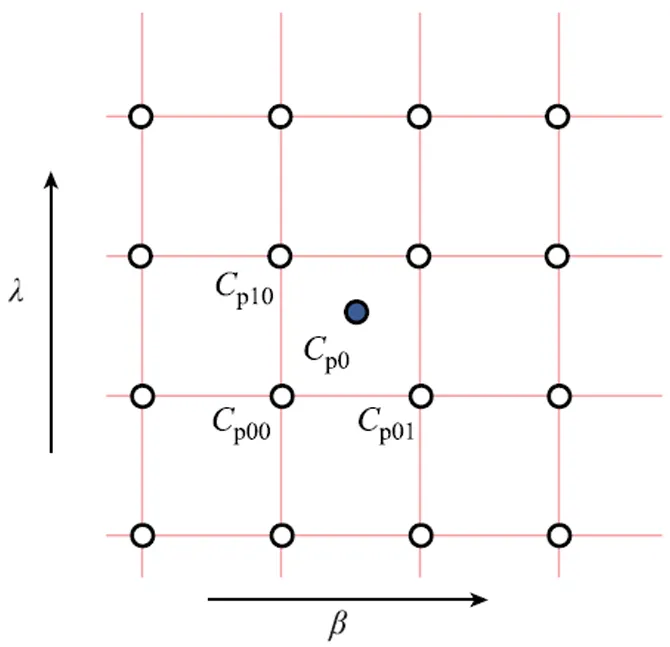
圖2 Cp的局部插值示意圖

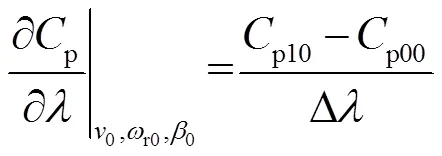
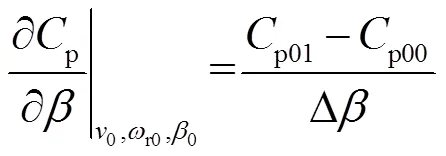
同理可得到t的相關偏導數的表達式為

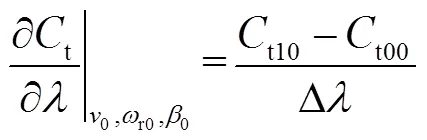
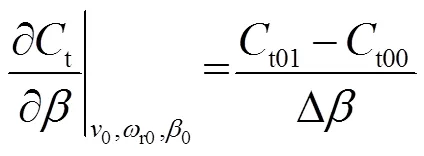
2 風電機組多入多出AGC控制模型

風輪機從風能中捕獲得到的機械功率可以由式（1）模型進行表示。根據該模型，若風電機組需要運行于AGC狀態，僅需調整p使其偏離最優值即可。根據風電機組工作原理，p的取值與和相關，且相同的p值可以對應于不同的和組合。

以常見的超速+變槳協調控制為例，當風電機組需要降功率時，該策略首先通過使轉子轉速超速來降低p。當轉子轉速增加到上限時，則通過增加槳距角進一步降低p。傳統AGC策略示意圖如圖3所示，所述過程如圖3中的箭頭所示。

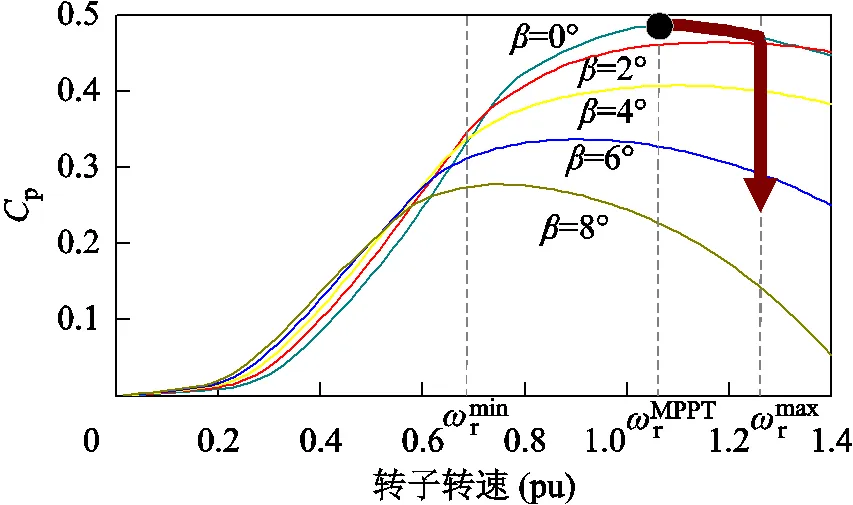
圖3 傳統AGC策略示意圖

研究人員認為，主軸轉矩s和塔根彎矩t的波動可用于計算風電機組的疲勞載荷，降低風電機組運行過程中s和t的標準差可降低機組疲勞。根據式（6）和式（8）可知，s、t與轉子轉速、槳距角的波動有直接關系。在如圖3所示的變速變槳控制中，槳距角的變化是在轉子轉速之后的，受到轉子轉速設定值的控制，因此在實現有功功率控制時不能使兩個參數同時自由調整，即難以進一步考慮對風電機組疲勞載荷的優化。

基于此，本文提出了一種AGC優化控制框架。在以上描述的有功功率優化控制框架下，可以將式（11）～式（26）所描述的線性化模型寫成狀態空間方程，即

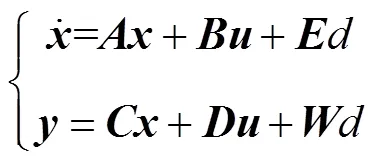
其中

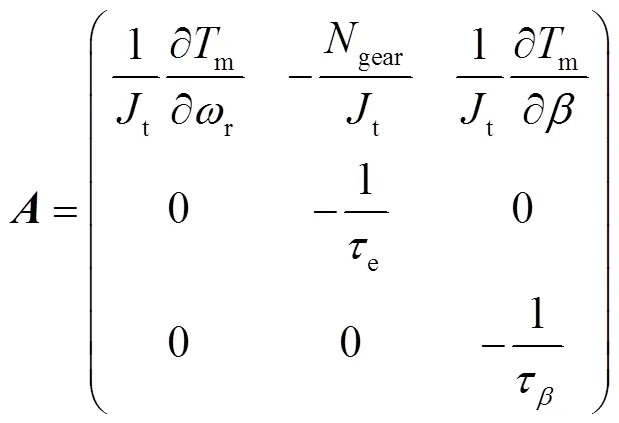
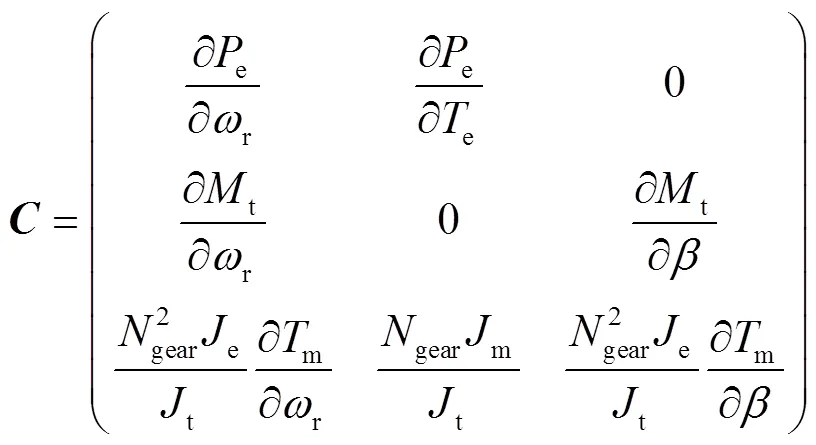
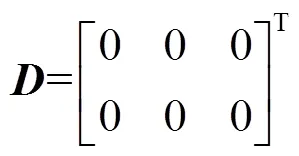
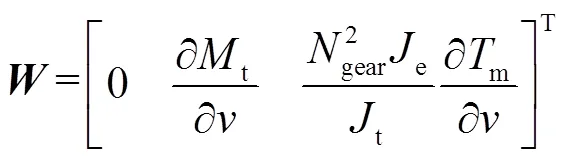
在式（27）所示模型中，風電機組有功控制系統的控制輸入為電磁轉矩和槳距角的變化量，輸出為有功功率、塔彎矩和主軸轉矩的變化量。基于上述模型，通過設計優化控制器，可以讓控制器同時生成電磁轉矩和槳距角的參考值，實現調度指令功率跟蹤，減少風電機組運行疲勞載荷。

3 風電場分布式AGC控制框架與求解算法

3.1 風電場分布式控制框架

風電場的AGC信號通常由風電場控制中心計算并分配給場內每臺風電機組。在這樣的分配過程中，難以根據風電機組的實際運行狀態和風況實施閉環控制。本文提出一種基于ADMM算法的DMPC框架進行風電機組參考功率的分配，由風電機組的本地控制器和風電場的控制中心協調實現，如圖4所示。該框架可以在完成風電場水平所需的功率的前提下，通過對每臺風電機組的優化控制進一步降低風電機組的疲勞載荷。

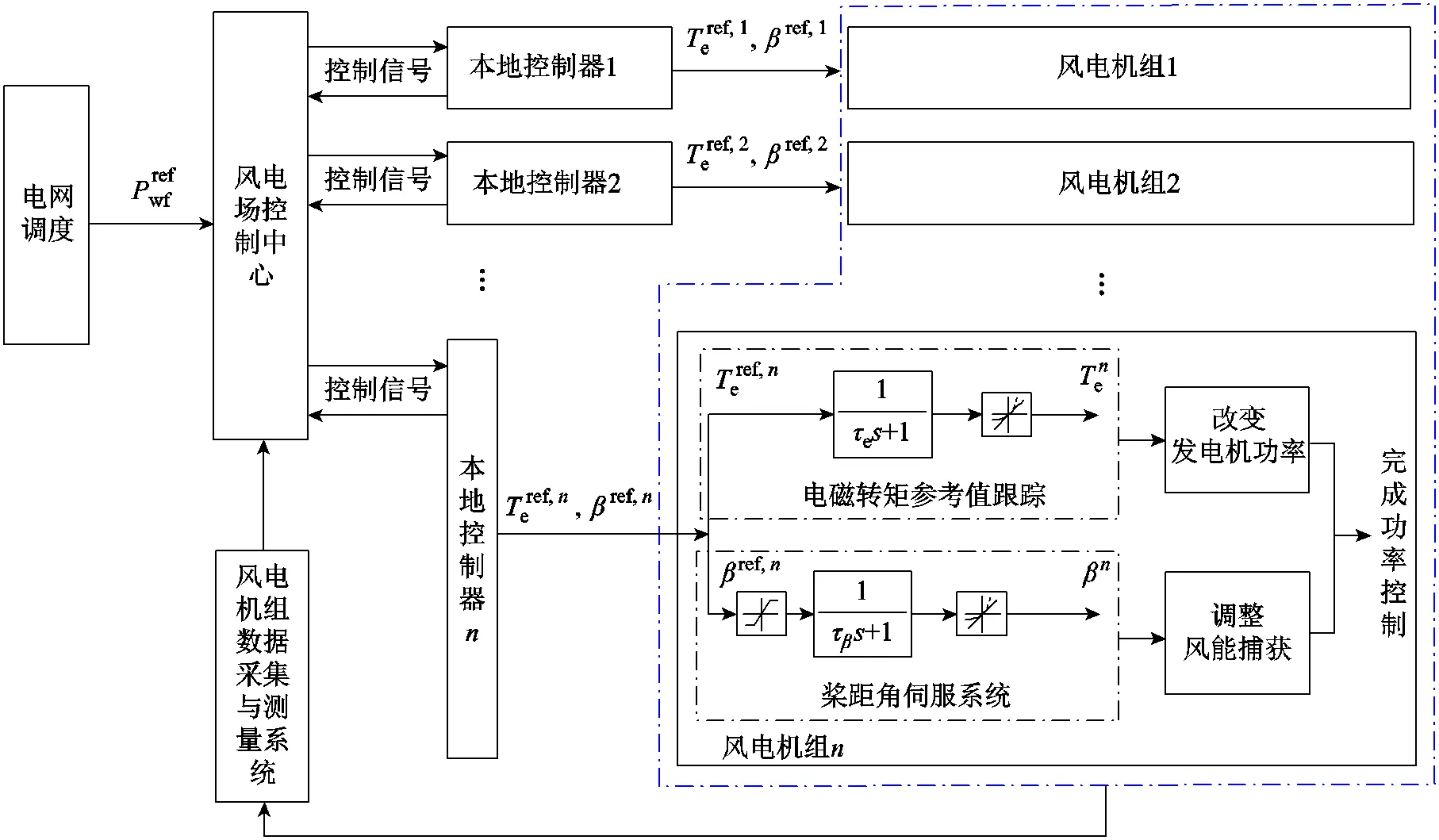
圖4 風電場分布式控制框架

在如圖4所示的風電場分布式AGC控制框架中，風電場控制中心在獲得調度中心下達的AGC控制指令后，與風電機組的本地控制器進行雙向的信息通信，完成3.3節中算法所需的參數迭代計算。通過中心控制器和本地控制器的協調計算，每臺風電機組均可獲得本機的電磁轉矩與槳距角設定值，通過本機執行機構中完成有功功率的跟蹤。同時，每臺風電機組均通過實時測量元件獲得包括機艙風速、轉子轉速以及槳距角等機組運行參數，反饋給機組的本地控制器，從而形成閉環控制。

值得注意的是，尾流效應和湍流強度作為影響風電場運行特性的重要因素，在風電場優化運行過程中必須考慮。更進一步地，在風電場AGC的過程中還需要考慮由于功率調整而產生的動態尾流。本文所建風電場模型在仿真中借助丹麥奧爾堡大學開發的Simwindfarm工具箱，在風電場優化中均考慮了基于Larsen模型的尾流計算和基于IEC 61400-3所規定的湍流模型，此處不再對相關模型進行詳細描述[28]。

在以上所述尾流及湍流模型的基礎上，對于仿真中的風電機組本地控制器，與其風速相關的狀態反饋來自所測量的本機機艙風速。

3.2 風電場AGC功率優化控制目標

采用第2節中所提風電機組AGC功率控制模型，風電機組的本地控制器可以計算單機層面的優化控制方案。進一步地，通過與風電場控制中心進行的信息共享和迭代，確保全場AGC功率總和滿足全局約束。根據以上定義，可將風電場有功功率的最佳控制的全局目標函數設置為式（28）和式（29），即

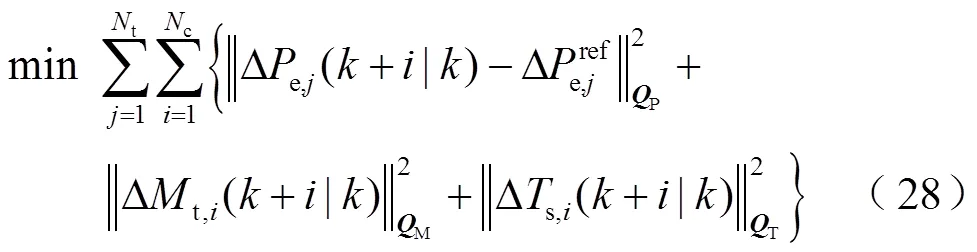
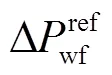
3.3 風電場分布式AGC求解算法

ADMM是乘子法的擴展，它允許采用分布式公式，在對偶公式中使用增廣拉格朗日函數，是一種收斂性較好的DMPC求解方法。針對3.2節中所描述的優化問題，采用ADMM進行求解的具體方法如下。

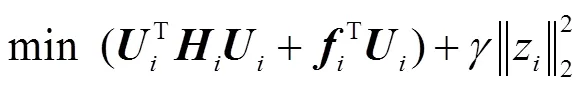
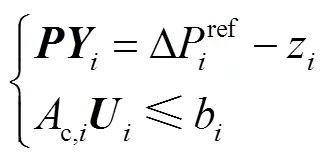
式中，c,i和b為將式（29）中的后三個約束轉換成標準二次規劃形式時獲得的約束矩陣。同時，

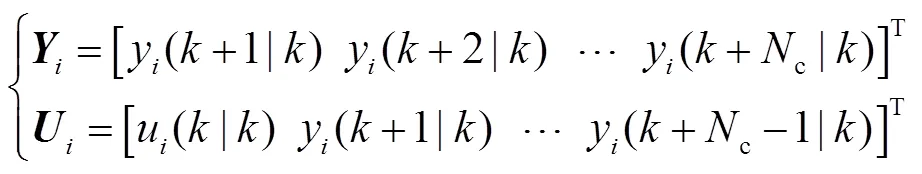
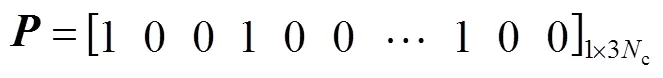
進一步地，可以得到ADMM算法所需增廣拉格朗日函數，即

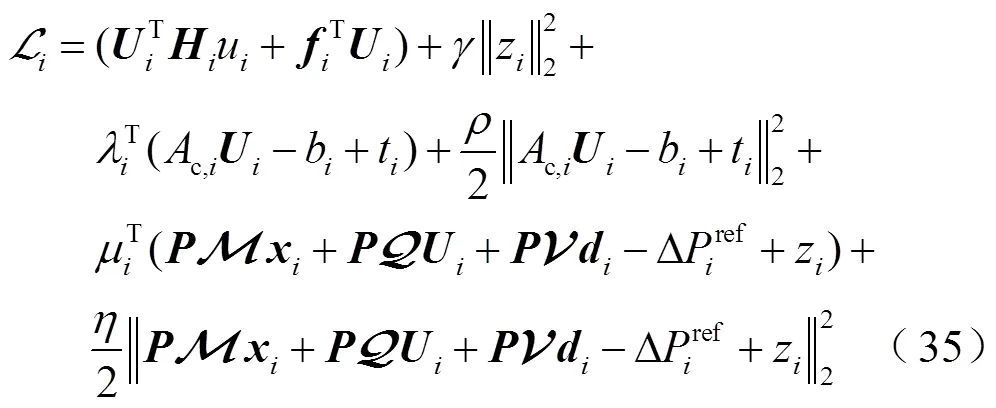
由于和是一個控制周期內的可測量參數，為簡化表達式，令

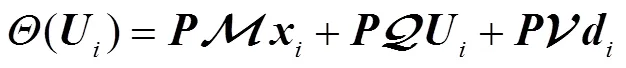
因此，可以推導出式（30）的求解公式為

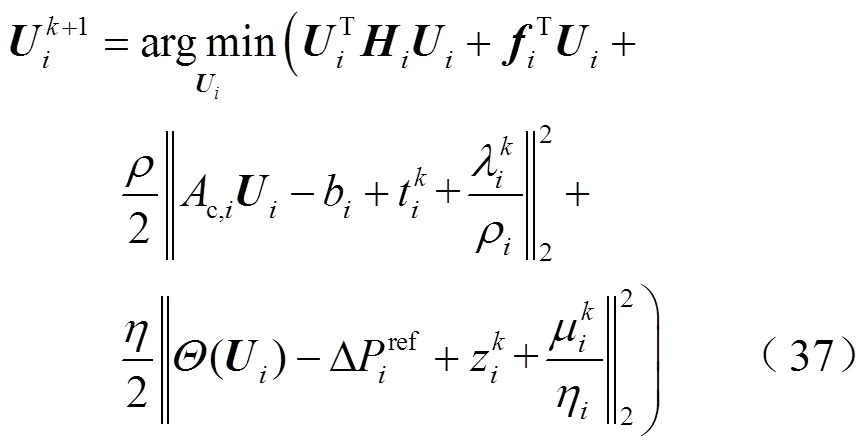
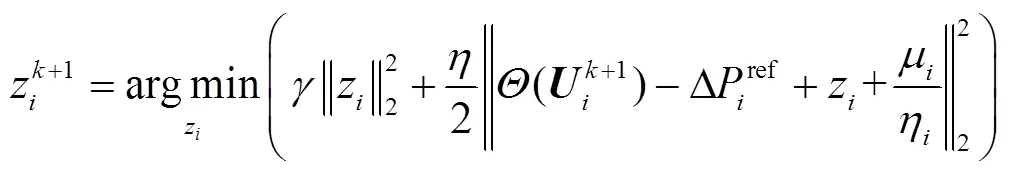
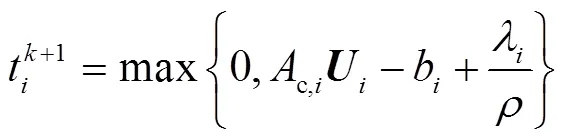
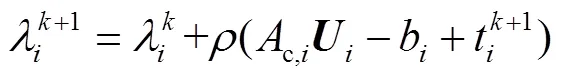
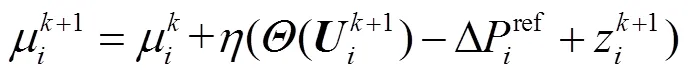
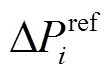
4 算例分析

4.1 仿真系統搭建

本文通過Matlab/Simulink搭建仿真系統以驗證本文所建風電機組多入多出控制模型和風電場分布式控制算法。用于做驗證的風電機組為NREL 5MW機組，主要參數如文獻[29]所介紹。在單機模型的基礎上，本文搭建了一個3×3排列的風電場模型，風機排列情況如圖5所示，場內風電機組之間的間距為400m。仿真過程中風電場的來流風速平均值為14m/s，湍流強度為0.1，場內尾流的計算基于Sim Wind Farm[28]，如圖6所示，場內9臺機組的風速波動范圍約為9～18m/s，覆蓋了機組多種運行工況。

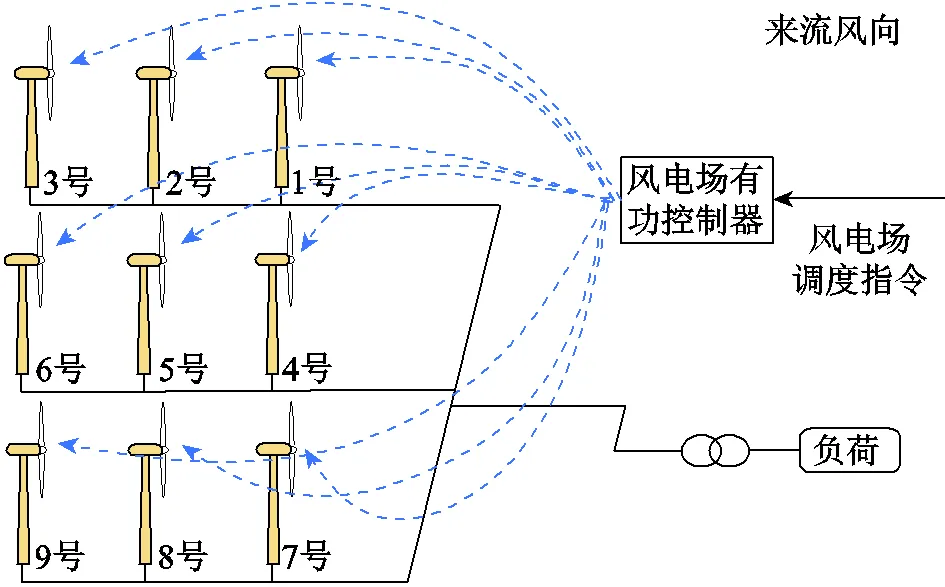
圖5 機組排布與尾流效果圖

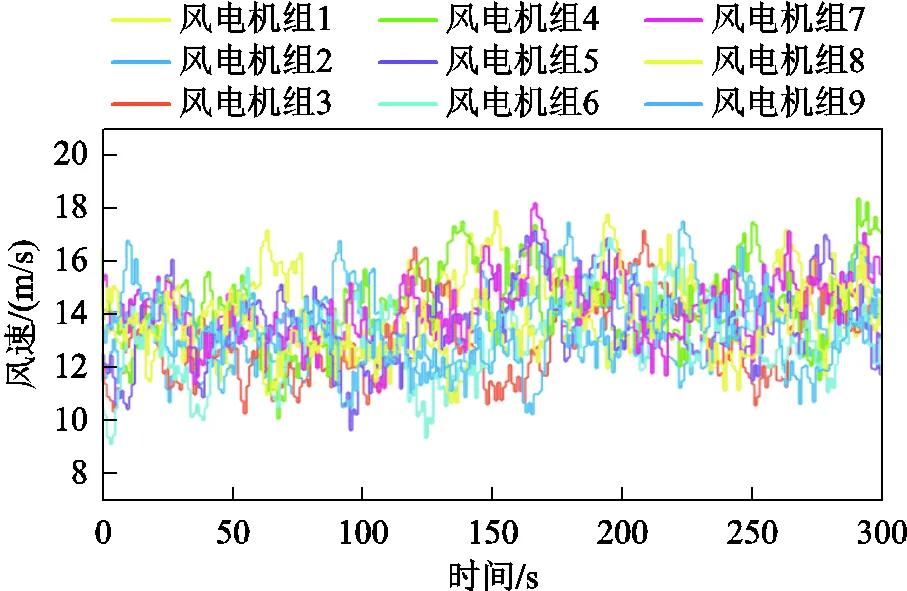
圖6 風電場9臺機組仿真風速

在仿真過程中，風電機組層面的控制方案由傳統的超速+變槳控制[30]與本文提出的多入多出控制模型進行對比；風電場層面的功率分配策略采用傳統的以最大發電能力計算的等比例分配策略[31]和本文提出的靈活分配策略進行對比；功率控制器則由傳統的PI控制器、MPC控制器[9]與本文提出的DMPC控制器相對比。仿真中策略的組合情況見表1。

表1 仿真中策略的組合情況

Tab.1 Combination of strategies in simulation

4.2 風電場AGC控制結果分析

以丹麥風電并網標準為例，風電場需要具備限制有功出力和功率爬坡的能力[32]。本算例中，風電場處于受調度指令控制的狀態，初始功率指令為25MW，60s時指令開始爬坡，180s時指令增加至30MW并一直保持恒定至300s。基于表1所示策略的風電場有功出力結果如圖7所示。

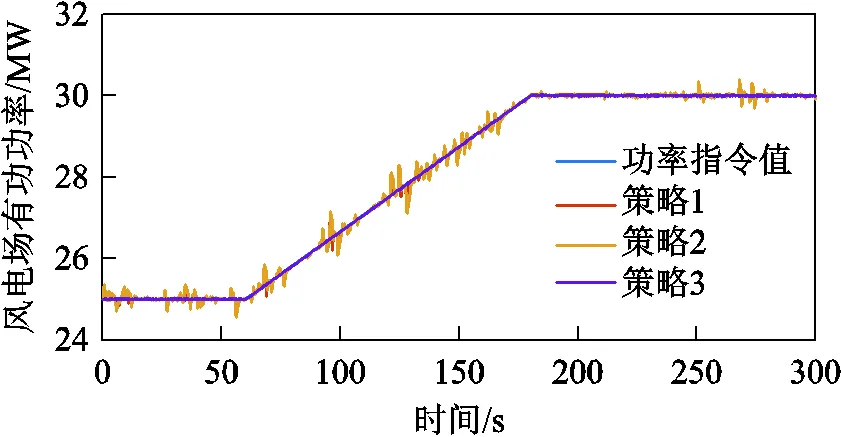
圖7 不同策略下風電場出力對比

由圖7可知三種策略均能有效實現風電場AGC功率指令值。其中，策略1和策略2的出力結果較指令值出現了明顯的毛刺，這是由于采用等比例分配時需通過風電機組風速的測量來計算機組的最大出力，再按比例進行功率分配。這一過程中存在風速測量誤差，從而導致最終的風電場輸出功率出現了與指令值的偏差。雖然三種策略都能夠較好地完成調度對風電場的AGC功率要求，但相比之下，采用功率靈活分配框架的策略3則更好地完成了調度指令。

進一步地，根據MCrunch算法計算得到場內風電機組在三種策略下的疲勞載荷情況見表2。

表2 不同策略下風電機組的損傷等效載荷

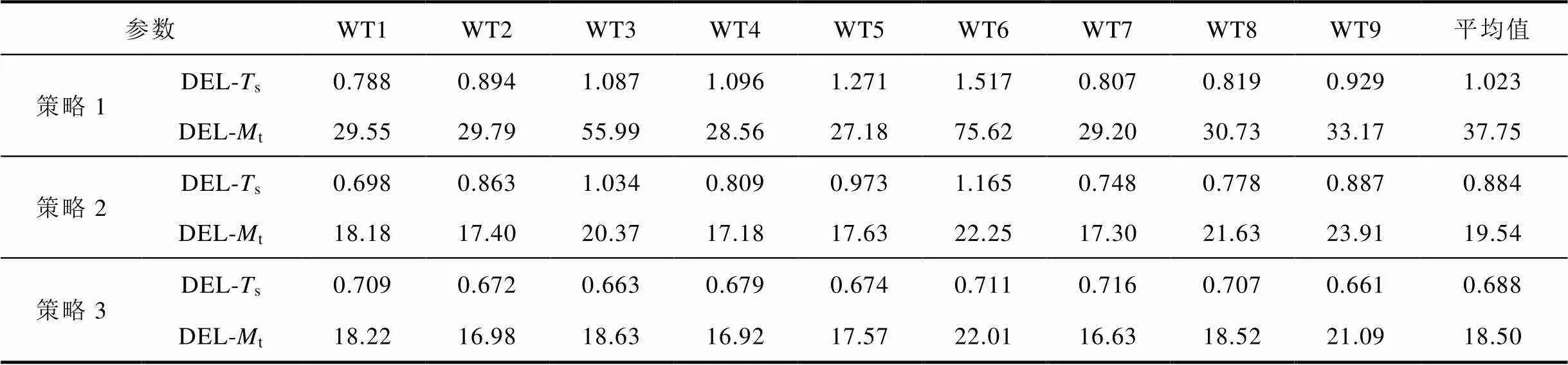
Tab.2 DELs of wind turbines under different strategies （單位：MN·m）

表2中，DEL-s和DEL-t分別為傳動系統和塔架對應的DEL值。由計算結果可以看出，對比策略1，由于策略2采用了本文提出的多入多出控制模型，對比傳統的機組控制方案，疲勞載荷得到了降低，全場機組傳動系統和塔架疲勞的平均值分別下降了12.3%和38.5%。然而策略2對場級功率分配沒有進行優化，本文所提的策略3通過進一步的優化分配，使得機組的疲勞載荷得到了更進一步的降低，全場機組傳統系統和塔架疲勞的平均值相對于策略2再次降低了22.2%和5.3%。

由此可見，在風電場層面，本文所建機組控制模型和分布式控制框架可以在完成調度要求的功率指令的前提下，有效降低機組的疲勞程度。

4.3 風電機組控制結果分析

4.2節從風電場層面討論了本文所建模型和所提控制策略的效果，可以看到風電場內所有機組的疲勞載荷較采用傳統的策略1均有了明顯降低，但各機組降低的程度有所不同。本節以采用策略1時疲勞載荷最高的6號風機（WT6）為例，分析各策略下風電機組層面的狀態變化情況。

WT6的機艙測量風速如圖8a所示，由于湍流的存在，風速在9～17m/s間波動。采用等比例分配時，低于額定風速會被分配比例較低的功率指令，因此有功功率如圖8b所示，策略1和策略2在圖8a中風速低于12m/s時功率都出現了明顯波動。而策略1和策略2都是工作于等比例分配的框架下，單機接收到功率指令值相同，因此出力也基本相同，這也進一步證實了本文所提控制模型的有效性。對于本文所提的策略3，由于采用了分布式的控制框架，在圖8b中，功率指令更為平滑。

在圖8c和圖8d中，采用策略2和策略3時可以同時調整轉速設定值和槳距角設定值，發電機轉速不需要一直限制在額定值附近波動，槳距角波動更為平緩。如圖8e和圖8f所示，這樣的狀態變化導致機組的主軸轉矩和塔根彎矩的波動在采用策略2和策略3時都更加平緩，尤其是采用策略3時，這與表2中的疲勞載荷結果相吻合。

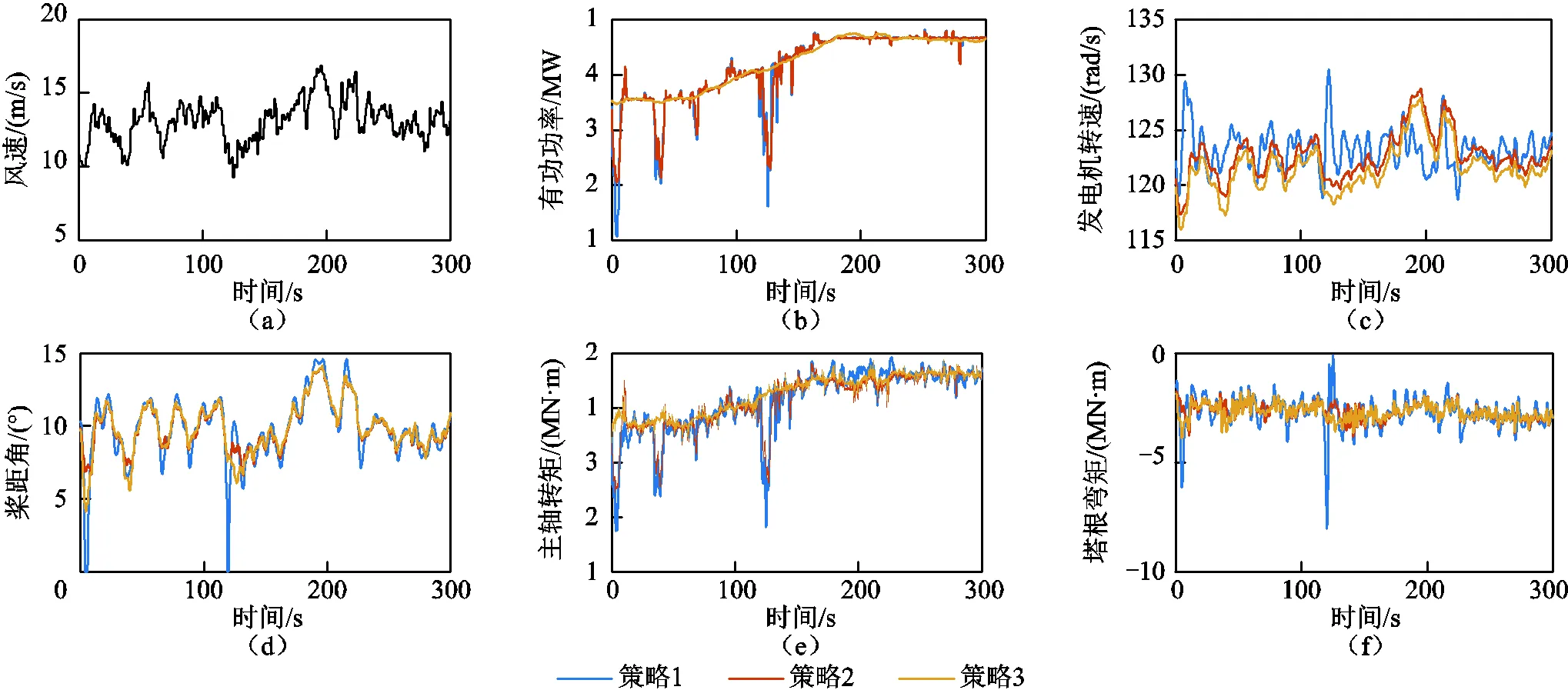
圖8 WT6機組在仿真過程中的狀態變化

5 結論

本文以風電場AGC控制過程為研究對象，在跟蹤調度指令的前提下，考慮在控制過程中的風電機組疲勞載荷優化問題，并就此提出了一種風電機組控制模型和分布式的風電場AGC框架，得出以下結論：

1）本文通過對風電機組非線性模型的線性化，建立了一種考慮有功功率輸出和疲勞載荷指標的多入多出線性模型，通過單一控制器可以完成對轉子轉速和槳距角的同時調整，較傳統控制方法更加靈活，可明顯降低機組運行的疲勞載荷。

2）本文建立了一種基于ADMM的風電場分布式AGC控制框架，實現對多入多出風電機組模型的有效控制，可以有效得完成調度設定的有功功率參考值，并且通過優化計算進一步降低機組運行的疲勞載荷。

[1] 穆鋼, 蔡婷婷, 嚴干貴, 等. 雙饋風電機組參與持續調頻的雙向功率約束及其影響[J]. 電工技術學報, 2019, 34(8): 1750-1759.

Mu Gang, Cai Tingting, Yan Gangui, et al. Bidirectional power constraints and influence of doubly fed induction generator participating in continuous frequency regulation[J]. Transaction of China Electrotechnical Society, 2019, 34(8): 1750-1759.

[2] Guo Xiaoqiang, Chen Weijian. Control of multiple power inverters for more electronics power systems: a review[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(3): 255-263.

[3] 王濤, 諸自強, 年珩. 非理想電網下雙饋風力發電系統運行技術綜述[J]. 電工技術學報, 2020, 35(3): 455-471.

Wang Tao, Zhu Ziqiang, Nian Hang. Review of operation technology of doubly-fed induction generator-based wind power system under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 579-587.2020, 35(3): 455-471.

[4] 麻秀范, 王戈, 朱思嘉, 等. 計及風電消納與發電集團利益的日前協調優化調度[J]. 電工技術學報, 2021, 36(3): 579-587.

Ma Xiufan, Wang Ge, Zhu Sijia, et al. Coordinated day-ahead optimal dispatch considering wind power consumption and the benefits of power generation group[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 579-587.

[5] 楊正清, 汪震, 展肖娜, 等. 考慮風電有功主動控制的兩階段系統備用雙層優化模型[J]. 電力系統自動化, 2016, 40(10): 31-37.

Yang Zhengqing, Wang Zhen, Zhan Xiaona, et al. Bi-level optimization model of two-stage reserve scheduling with proactive wind power control[J]. Automation of Electric Power Systems, 2016, 40(10): 31-37.

[6] Guo Yifei, Gao Houlei, Wu Qiuwei, et al. Distributed coordinated active and reactive power control of wind farms based on model predictive control[J]. International Journal of Electrical Power & Energy Systems, 2019, 104: 78-88.

[7] Hu Jianqiang, Chen M Z Q, Cao Jinde, et al. Coordinated active power dispatch for a microgrid via distributed lambda iteration[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2017, 7(2): 250-261.

[8] 蘇永新, 段斌, 朱廣輝, 等. 海上風電場疲勞分布與有功功率統一控制[J]. 電工技術學報, 2015, 30(22): 190-198.

Su Yongxin, Duan Bin, Zhu Guanghui, et al. Fatigue distribution and active power combined control in offshore wind farm[J]. Transaction of China Electrotechnical Society, 2015, 30(22): 190-198.

[9] Riverso S, Mancini S, Sarzo F, et al. Model predictive controllers for reduction of mechanical fatigue in wind farms[J]. IEEE Transactions on Control Systems Technology, 2017, 25(2): 535-549.

[10] Zhao Haoran, Wu Qiuwei, Huang Shaojun, et al. Fatigue load sensitivity-based optimal active power dispatch for wind farms[J]. IEEE Transactions on Sustainable Energy, 2017, 8(3): 1247-1259.

[11] Knudsen T, Bak T, Svenstrup M. Survey of wind farm control-power and fatigue optimization[J]. Wind Energy, 2015, 18(8): 1333-1351.

[12] Zhang Baohua, Soltani M, Hu Weihao, et al. Optimized power dispatch in wind farms for power maximizing considering fatigue loads[J]. IEEE Transactions on Sustainable Energy, 2018, 9(2): 862-871.

[13] 劉吉臻, 孟洪民, 胡陽. 采用梯度估計的風力發電系統最優轉矩最大功率點追蹤效率優化[J]. 中國電機工程學報, 2015, 35(10): 2367-2374.

Liu Jizhen, Meng Hongmin, Hu Yang. Efficiency optimization of optimum torque maximum power point tracking based on gradient approximation for wind turbine generator system[J]. Proceedings of the CSEE, 2015, 35(10): 2367-2374.

[14] 姚琦, 劉吉臻, 胡陽, 等. 含異步變速風機的風電場一次調頻等值建模與仿真[J]. 電力系統自動化, 2019, 43(23): 185-192.

Yao Qi, Liu Jizhen, Hu Yang, et al. Equivalent modeling and simulation for primary frequency regulation of wind farm with asynchronous variable-speed wind turbines[J]. Automation of Electric Power Systems, 2019, 43(23): 185-192.

[15] Wang Shu, Seiler P. LPV Active power control and robust analysis for wind turbines[C]//33rd Wind Energy Symposium, Kissimmee, Florida: American Institute of Aeronautics and Astronautics, 2015.

[16] 劉軍, 張彬彬, 趙婷. 基于模糊評價的風電場有功功率分配算法[J]. 電工技術學報, 2019, 34(4): 786-794.

Liu Jun, Zhang Binbin, Zhao Ting. Research on wind farm active power dispatching algorithm based on fuzzy evaluation[J]. Transaction of China Electrotechnical Society, 2019, 34(4): 786-794.

[17] Zhao Haoran, Wu Qiuwei, Guo Qinglai, et al. Distributed model predictive control of a wind farm for optimal active power control part I: clustering-based wind turbine model linearization[J]. IEEE Transactions on Sustainable Energy, 2015, 6(3): 831-839.

[18] Luo Haocheng, Hu Zechun, Zhang Hongcai, et al. Coordinated active power control strategy for deloaded wind turbines to improve regulation performance in AGC[J]. IEEE Transactions on Power Systems, 2019, 34(1): 98-108.

[19] Tang Xuesong, Yin Minghui, Shen Chun, et al. Active power control of wind turbine generators via coordinated rotor speed and pitch angle regulation[J]. IEEE Transactions on Sustainable Energy, 2019, 10(2): 822-832.

[20] Hoek D van der, Kanev S, Engels W. Comparison of down-regulation strategies for wind farm control and their effects on fatigue loads[C]//2018 Annual American Control Conference (ACC), 2018: 3116-3121.

[21] Spudic V. Coordinated optimal control of wind farm active power[D]. Croatia: University of Zagreb, 2012.

[22] Jin Jingliang, Zhou Dequn, Zhou Peng, et al. Dispatching strategies for coordinating environmental awareness and risk perception in wind power integrated system[J]. Energy, 2016, 106: 453-463.

[23] Zhang Jinhua, Liu Yongqian, Infield D, et al. Optimal power dispatch within wind farm based on two approaches to wind turbine classification[J]. Renewable Energy, 2017, 102: 487-501.

[24] Wang Lei, Wen Jie, Cai Ming, et al. Distributed Optimization control schemes applied on offshore wind farm active power regulation[J]. Energy Procedia, 2017, 105: 1192-1198.

[25] Yao Qi, Hu Yang, Chen Zhe, et al. Active power dispatch strategy of the wind farm based on improved multi-agent consistency algorithm[J]. IET Renewable Power Generation, 2019, 13(14): 2693-2704.

[26] Zhao Haoran, Wu Qiuwei, Guo Qinglai, et al. Distributed model predictive control of a wind farm for optimal active power control part II: implementation with clustering-based piece-wise affine wind turbine model[J]. IEEE Transactions on Sustainable Energy, 2015, 6(3): 840-849.

[27] 李世春, 黃悅華, 王凌云, 等. 基于轉速控制的雙饋風電機組一次調頻輔助控制系統建模[J]. 中國電機工程學報, 2017, 37(24): 7077-7086, 7422.

Li Shichun, Huang Yuehua, Wang Lingyun, et al. Modeling primary frequency regulation auxiliary control system of doubly fed induction generator based on rotor speed control[J]. Proceedings of the CSEE, 2017, 37(24): 7077-7086, 7422.

[28] Aalborg University. SimWindFarm Toolbox[EB/OL]. /2020-03-07. http://www.ict-aeolus.eu/SimWindFarm/ index.html.

[29] Jonkman J, Butterfield S, Musial W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. NREL/TP-500-38060, 947422, 2009.

[30] Yao Qi, Liu Jizhen, Hu Yang. Optimized active power dispatching strategy considering fatigue load of wind turbines during de-loading operation[J]. IEEE Access, 2019, 7: 17439-17449.

[31] Merahi F, Berkouk E, Mekhilef S. New management structure of active and reactive power of a large wind farm based on multilevel converter[J]. Renewable Energy, 2014, 68: 814-828.

[32] Regulations for grid connection | Energinet[EB/OL]. 2019-10-24. https://en.energinet.dk/Electricity/Rules- and-Regulations/Regulations-for-grid-connection.

Distributed Automatic Generation Control of Wind Farm Considering Load Suppression

Yao Qi1Hu Yang2Liu Yu3Luo Zhiling2Qi Xiao1

（1. Energy and Electricity Research Center Jinan University Zhuhai 519070 China 2. School of Control and Computer Engineering North China Electric Power University Beijing 102206 China 3. North Electric Power Dispatch and Control Sub-Center State Grid Corporation of China Beijing 100053 China）

To optimize the fatigue load of wind turbines during automatic generation control (AGC) process, a novel wind turbine control model was proposed and applies it to the wind farm. A multi-input and multi-output (MIMO) wind turbine control model was established, so that the wind turbine can control the rotor speed and pitch angle simultaneously. Then, a wind farm control system based on a distributed framework was designed to make wind turbines coordinate with each other to directly optimize the rotor speed and pitch angle of all turbines with the goal of load suppression. The simulation results show that the proposed control model can achieve more flexible and effective control of wind turbines. Combined with the distributed control framework, the fatigue load of wind turbines can be significantly reduced under the premise of completing AGC instructions.

Automatic generation control(AGC), fatigue load, wind farm, distributed control

10.19595/j.cnki.1000-6753.tces.201602

TM614

廣東省基礎與應用基礎研究基金青年基金（2020A1515110547）和國家自然科學基金聯合基金（U1766204）資助項目。

2020-12-07

2021-03-18

姚 琦 男，1994年生，博士，講師，研究方向為風力發電系統及其控制。E-mail：qiyao@jnu.edu.cn

綦 曉 男，1992年生，博士，講師，研究方向為綜合能源系統控制。E-mail：qixiao@jnu.edu.cn （通信作者）

（編輯 赫蕾）