不同巷道斷面形狀對圍巖穩定性的數值模擬研究

段燕偉DUAN Yan-wei

（黑龍江科技大學，哈爾濱 150022）

0 引言

巷道斷面形狀是影響圍巖穩定性的關鍵因素，不同的斷面形狀將影響巷道圍巖的應力分布，從而產生不同的圍巖狀態。不同斷面形狀的巷道難以在同一地質條件下實現，而數值模擬可以輕松實現同一地質條件下不同工況的研究。因此借助數值模擬的手段，可以研究同一地質條件下不同巷道形狀對巷道圍巖穩定性的影響。

鑒于此，國內學者借助數值模擬軟件做出了大量研究，姬書強[1]采用有限元軟件，研究了圍巖力學性能的影響。李曉斌[2]等通過數值模擬對矩形和直墻平頂肩角微拱形厚頂煤巷道應力分布特征進行了對比分析。程國棟[3]采用PFC 2D軟件研究分析了6種不同斷面形狀的巷道圍巖變形破裂特征。張一夫[4]等利用有限體積法對不同巷道斷面形狀的圍巖進行數值模擬，并定量分析巷道斷面形狀對圍巖的影響。張曉剛[5]等通過數值模擬和現場試驗對深井軟巖巷道的穩定性進行了研究，并由此提出了支護方案。郭曉菲[6]等結合蝶形破壞理論對不同巷道斷面形狀的適用性進行了探討。劉康等[7]開展了臨近爆破條件下巷道斷面形狀對圍巖裂紋擴展規律的研究。董紅娟[8]等利用FLAC3D數值模擬軟件對巷道斷面形狀進行了模擬分析，得出最優巷道形狀，并應用于現場。王克義[9]利用數值模擬手段對不同斷面形狀下巷道圍巖的穩定性進行了分析，并提出合理的支護參數。王剛[10]模擬分析了三種不同斷面形狀巷道的破壞特征和圍巖變形量，得出最優斷面，并提出支護方案。張進鵬[11]等分析了大傾角煤巖層條件下，對半圓拱形、斜頂梯形以及偏心圓弧形巷道的圍巖穩定性進行分析，并從耦合支護的角度，選擇最優的巷道形狀。李曉斌[12]等針對厚煤層矩形巷道支護困難的問題，利用數值模擬研究，改進了巷道形狀，采用直墻平頂肩角微拱形，對支護難題有所改善。以上研究均針對某一種特定地質條件，利用數值模擬，從巷道圍巖應力環境進行分析，但對于不同斷面形狀巷道圍巖的應力、變形和塑性區域較為全面的研究相對不足。

本文為研究斷面形狀對巷道圍巖穩定性的影響，利用數值模擬軟件FLAC3D對矩形、梯形和直墻圓拱形三種斷面形狀的巷道進行了模擬，并全面分析了不同斷面形狀巷道圍巖的應力特征、變形特征和塑性區域的分布規律，從而選取該地質條件下最佳巷道斷面形狀，為解決工程問題提供依據，同時為類似工程提供借鑒。

1 工程背景

紅慶梁煤礦3-1煤層為主采煤層，厚度為4.7m～5.7m，平均煤厚為5.15m。煤層傾角為0-6°，平均傾角為3°。3-1號煤層結構簡單，呈黑色，瀝青光澤，參差狀、棱角狀斷口，內生裂隙較發育，常為黃鐵礦及方解石薄膜充填，條帶狀結構，屬半暗型煤。局部含1層夾矸，厚度為0.15～1.0m，夾矸巖性為砂質泥巖或砂巖。

11303 綜采工作面沿煤層傾向布置，工作面順槽沿煤層走向布置。該工作面位于3-1煤輔助運輸大巷西部，走向長為4290m，傾向長為275m。11303工作面回風巷頂板為細砂巖，呈灰色，局部含植物化石，平行層理發育；底板為泥巖，灰色，局部含植物化石，巖屑及云母碎片，泥巖膠結。在現有支護條件下，底鼓現象嚴重，影響正常生產。

2 模擬方案

本次數值模擬以紅慶梁煤礦11303回風巷為工程背景，根據工程地質條件，建立模型。模擬區域為長×寬×高=50m×30m×45m，其中矩形巷道斷面為寬×高=5.5m×4m，梯形巷道斷面為上底/下底×高=4.5m/5.5m×4m，直墻圓拱形巷道斷面為寬5.5m，拱形半徑為2.75m，墻高為1.25m。模型網格采用“中間密四周疏”的劃分原則，以底板左下角為坐標原點，傾向為x軸方向，走向為y軸方向，重力方向為z軸方向。

模型整體采用Mohr-Coulomb力學模型，巷道開挖采用null模型代替。該模型限制其側向和底部處位移，在上表面施加12.2 MPa的等效荷載，模擬上覆巖體的自重條件。表1為圍巖力學參數。模擬深入揭示不同巷道斷面形狀開挖穩定后圍巖應力特征、變形特征、圍巖塑性區分布規律。

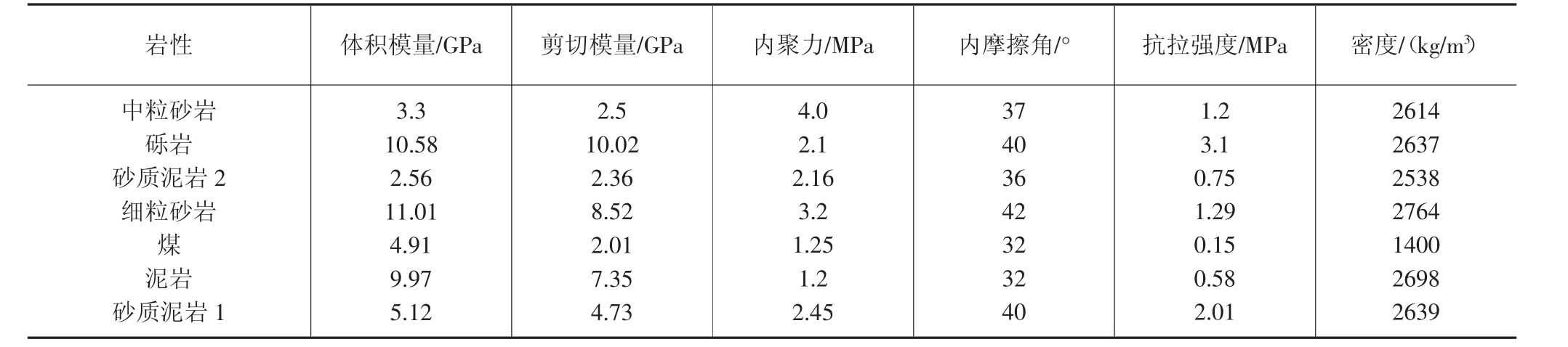
表1 圍巖力學參數

3 結果分析

3.1 巷道圍巖應力特征

圖1為不同形狀巷道圍巖垂直應力云圖。由圖可知，①不同形狀巷道圍巖垂直應力分布規律一致，巷道兩幫為高應力區域，兩幫以橢圓形式向兩側擴散；頂底板為低應力區域，以半圓的形式向兩側擴散，最終過渡為原巖應力區域。

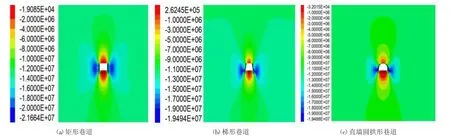
圖1 不同形狀巷道垂直應力云圖

②不同形狀的巷道應力區域分布略有不同：就兩幫高應力區域而言，矩形巷道高應力區域最大，直墻圓拱形巷道最小，梯形巷道居中；對于巷道頂底板的低應力區域因巷道形狀而異，梯形巷道和直墻圓拱形巷道頂底板應力不對稱，頂板低應力區域相對較小。

③不同形狀巷道的應力峰值不同，矩形巷道高應力峰值為21.66MPa，梯形巷道為19.49MPa，直墻圓拱形為19.45MPa，應力集中系數從1.86降到了1.59。因此，巷道形狀影響巷道圍巖應力環境，三種巷道形狀中，直墻圓拱形巷道兩幫高應力區域最小，且高應力最大值較小；頂底板應力分布均勻，直墻圓拱形巷道更利于巷道穩定。

為分析巷道圍巖的應力變化特征，分別沿巷道頂底板（中部）、右幫（距底板2m）、頂角和底角位置（與水平方向呈45°夾角方向），設置測線，側線長度為15m，每隔1m設置一個測點。不同形狀巷道條件下，不同位置的應力變化不同：頂、底板和右幫垂直應力變化規律相似，不同巷道的應力差值不大；巷道底角垂直應力變化為先增大后減小，梯形和直墻圓拱形巷道底角垂直應力變化規律相似，而矩形巷道底角垂直應力整體偏低；梯形巷道頂角垂直應力整體偏低，且在8m范圍內遠低于原巖應力，而直墻圓拱形巷道頂角相對穩定，有利于巷道的整體穩定。綜上所述，從巷道應力分布來看，直墻圓拱形巷道應力分布較為均勻，高應力區域較小，整體穩定性最好。

3.2 巷道圍巖變形特征

圖2為不同巷道寬高比圍巖垂直位移云圖。由圖可知，①巷道掘進穩定后，垂直位移分布呈對稱分布，垂直位移主要發生在巷道頂底板。從分布范圍來看，頂板分布范圍較小，底板分布范圍較大。從位移值上來看，頂板垂直位移較大。

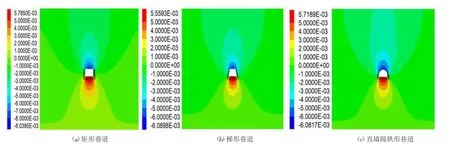
圖2 不同形狀巷道垂直位移云圖

②對比三種巷道斷面形狀的垂直位移，矩形巷道頂板位移最大為8.04mm，梯形巷道和直墻圓拱形巷道頂板位移較小，分別為6.09mm和6.08mm。矩形巷道和直墻圓拱形巷道底板位移較大，分別為5.79mm和5.72mm，梯形巷道底板位移為5.56mm。綜上所述，巷道形狀對于巷道圍巖變形有較大影響，直墻圓拱形巷道底板變形量相對較小，底鼓范圍也相對較小，因此直墻圓拱形巷道圍巖變形量最小，巷道圍巖更穩定。

3.3 巷道圍巖塑性區分布

圖3為不同形狀巷道塑性區域分布圖。由圖可知，①不同形狀的巷道圍巖塑性區破壞方式基本一致，破壞形態為“X”型，頂底板為拉伸破壞，巷幫及頂底角位置為剪切破壞。②與直墻圓拱形相比，梯形巷道和矩形巷道塑性破壞范圍稍大，尤其體現在頂板和頂角位置，這與垂直應力分布結果一致，頂底角是巷道圍巖變形破壞的關鍵位置。③整體來看，三種形狀巷道底角的剪切破壞比較嚴重，直墻圓拱形巷道底角塑性區域相對較小，這是因為圓拱形巷道應力分布均勻，不易形成應力集中，從而使巷道圍巖應力處于相對平衡的狀態，不易發生較大范圍的塑性破壞。綜上所述，巷道形狀為直墻圓拱形時，巷道圍巖塑性區域最小，更有利于巷道圍巖穩定。

圖3 不同形狀巷道塑性區域分布

4 結論及建議

①不同形狀巷道的應力峰值不同，矩形巷道高應力峰值為21.66MPa，梯形巷道為19.49MPa，直墻圓拱形為19.45MPa，應力集中系數從1.86降到了1.59。巷道底角垂直應力變化為先增大后減小，梯形和直墻圓拱形巷道底角垂直應力變化規律相似，而矩形巷道底角垂直應力整體偏低；梯形巷道頂角垂直應力整體偏低，且在8m范圍內遠低于原巖應力，而直墻圓拱形巷道頂角相對穩定，有利于巷道的整體穩定。

②垂直位移主要發生在巷道頂底板。從矩形到梯形再到直墻圓拱形巷道，頂底板的位移范圍變小，且垂直位移峰值也變大，底板垂直位移從8.04mm增加到6.08mm，頂板垂直位移從5.79mm降低到5.71mm。這表明直墻圓拱形巷道圍巖變形量最小。

③巷道圍巖塑性區破壞方式基本一致，頂底板為拉伸破壞，巷幫及頂底角位置為剪切破壞。與直墻圓拱形巷道相比，梯形巷道和矩形巷道塑性破壞范圍稍大，尤其體現在頂板和頂角位置，且直墻圓拱形巷道頂板塑性破壞范圍最小。

④通過從應力特征、變形特征和塑性區域分布三個方面，分析矩形、梯形和直墻圓拱形三種斷面形狀的巷道圍巖穩定性，建議采用直墻圓拱形巷道，該形狀斷面巷道圍巖穩定性最好，從模擬結果上來看，可以較好地解決底鼓問題。