基于改進啟發式蟻群算法的無人機自主航跡規劃

辛建霖，左家亮，岳龍飛，張宏宏

（空軍工程大學 空管領航學院，西安 710051）

0 引 言

隨著科學技術的發展，現代戰爭信息化、智能化程度逐漸提高，使得無人機的應用發展受到更多關注。無人機航跡規劃是無人機作戰應用的關鍵環節，其目的是在滿足各種約束條件的前提下（無人機性能、飛行安全性、任務目標等），尋找到一條最優或較優航跡。航跡規劃經歷了從手動繪制到計算機自動解算兩個階段，研究內容主要包括：地形和威脅等環境要素的表示方法分析、基于任務需求的目標函數構造、滿足飛行距離和轉彎半徑等限制因素的約束條件處理、針對實時性和協同性等需求的航跡搜索算法研究。現有的航跡規劃已可以滿足一定的應用需求，例如，田疆等提出了一種改進連接型快速擴展隨機樹算法，可用于復雜環境下的無人機三維航跡規劃，但在實時性、高效性、協同航跡規劃和可替換航跡規劃等方面仍然存在一些不足。

航跡規劃算法主要分為兩大類，一類是經典算法，如最優控制法、動態規劃法等；另一類是智能算法，如人工勢場法、粒子群算法、遺傳算法、蟻群算法等。最優控制法把航跡規劃問題轉化為最優控制問題，建立最優控制模型進行求解，但這種方法對初始值要求較高，建模和求解較為復雜。遺傳算法模擬生物遺傳進化過程，求解航跡規劃問題高效、魯棒性強，但算法容易早熟收斂，局部搜索能力較差。李涵等在殲轟機突防突擊過程中，運用改進的遺傳算法進行了航線規劃，但其計算模型考慮因素較少，模型尚不完善。蟻群算法（Ant Colony Algorithm，簡稱ACO）是一種基于對螞蟻群體覓食行為的研究而提出的搜索算法，具有魯棒性好、正反饋能力強的優點，但面對復雜問題時，容易出現算法停滯、陷入局部最優、運算時間過長等問題。為此，國內外對ACO 算法提出了許多改進措施。陳雄等對信息素揮發系數進行動態調整，用優化參數的方式有效解決了算法停滯的問題，但改進后算法不夠靈活；B. Bulln?heimer 等引入精英螞蟻策略，通過改進算法結構提高最優和次優路徑的引導能力，但收斂速度較慢；Wang L 等采用融合遺傳算法的方式提升ACO 算法的尋優能力，但算法適應性較差。

本文提出一種改進啟發式蟻群算法（Im?proved Heuristic Ant Colony Algorithm，簡稱IHACO）的無人機自主航跡規劃算法，通過引入Dijk?stra 算法、Logistic 混沌映射、多航跡選擇策略、模擬退火機制的方法對ACO 算法進行改進，以提高算法初期的搜索效率，增強全局尋優能力，平衡收斂速度與全局尋優能力之間的矛盾，增強算法在復雜環境中的搜索性能，并對算法進行仿真分析。

1 航跡規劃問題描述及環境建模

1.1 問題描述

針對無人機在作戰任務中穿越地形障礙、躲避敵方地對空導彈威脅的航跡規劃，簡化運行環境并進行如下假設：（1）簡化模型，將無人機簡化為質點；（2）假設無人機在執行任務中，保持一定的飛行高度和速度，在二維有限空間進行移動；（3）假設地形障礙、地空導彈火力覆蓋范圍已知，并用多邊形進行表示（通常地空導彈火力覆蓋為圓形區，這里簡化模型，用正方形區域表示）。

1.2 空間建模

在航跡規劃中，常用的空間建模方法有VOR?ONOI 法、柵格圖法、鏈接圖法等，其中鏈接圖法具有簡化模型占用內存少、效果好的優點，故本文采用鏈接圖法構造二維空間模型，生成規劃可用空間，如圖1 所示，在MATLAB 環境中構造200 km×200 km 的二維空間，存在4 個不規則多邊形表示的障礙區域、多條自由鏈接線（黑色虛線表示）和初始點和終止點，鏈接各鏈接線中點、初始點和終止點，生成初始航跡規劃網絡圖（黑色實線表示）。

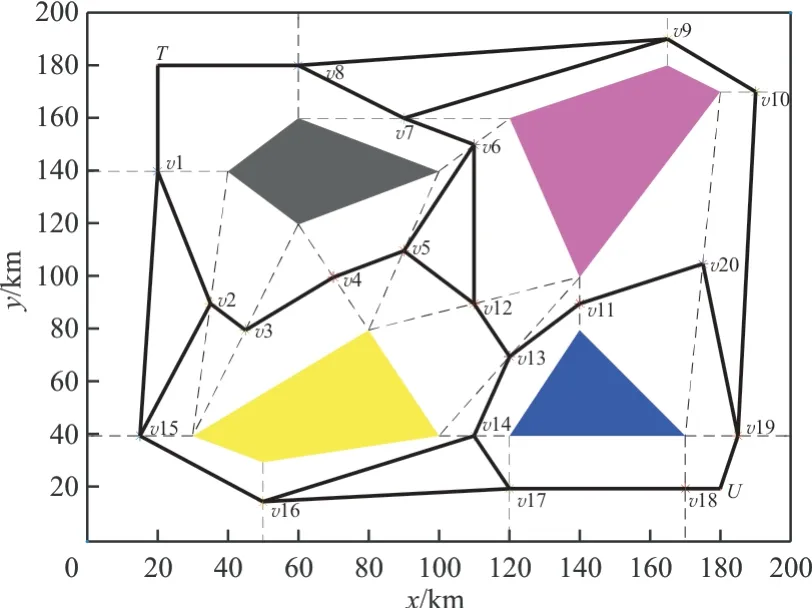
圖1 鏈接圖法構造二維空間模型圖Fig.1 Construction of two dimensional space model graph by link graph method

1.3 航跡點的構造

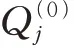
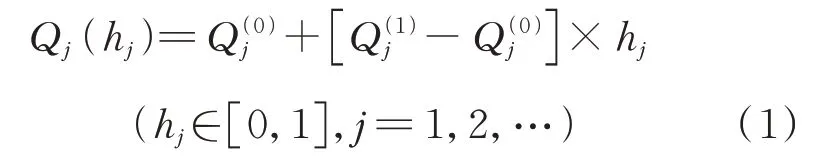
式中：h為比例參數；為與航跡相交的鏈接線數。

通過式（1）可知，用，，…，h，和可以表示一條從起始點到終止點的航跡。

1.4 建立目標函數

在無人機飛行穿越地形障礙、躲避敵方地對空導彈威脅時需要進行航跡規劃，航跡規劃的任務是根據起始點和目標點的位置，在避開地形障礙區、導彈威脅區的前提下，找到一條最短航跡，保證無人機能夠安全、快速通過。目標函數為

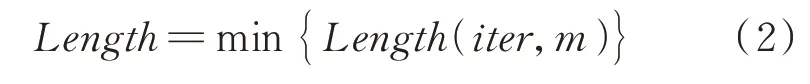
式中：(，)為航跡長度（在第次迭代第只螞蟻的情況）。

2 蟻群算法改進

2.1 Dijkstra 算法規劃初始航跡

為了改善ACO 算法前期搜索效率差的問題，運用典型的最短路徑算法，在算法求解出一個節點到其他節點的最短航跡的基礎上，確定起始點到終止點的一條較優航跡，以減少ACO 算法前期搜索的盲目性。Dijkstra 算法的基本思想是先把二維模型中的節點分為兩組，一組為已確定最短航跡的節點，另一組為未確定最短航跡的節點，按最短航跡長度遞增的順序逐個把未確定的節點加入已確定的一組中，直到所有節點都成為已確定的節點，即可得到一條從初始點到終止點的較優航跡。Dijkstra 算法流程如圖2 所示。

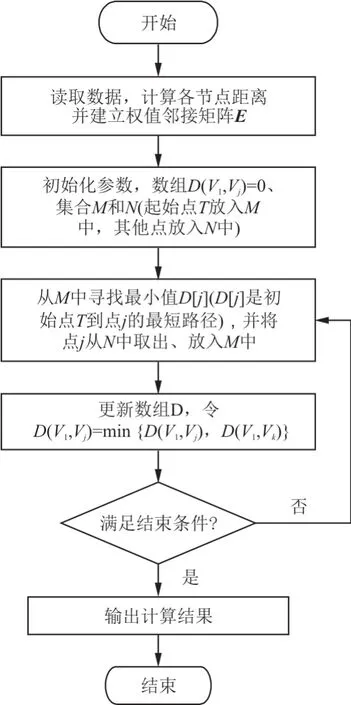
圖2 Dijkstra 算法初始化航跡流程圖［20］Fig.2 Flow chart of Dijkstra algorithm initialization track［20］

2.2 引入Logistic 混沌映射初始化信息素

為了避免蟻群停滯在局部搜索，提高算法收斂速度，引入混沌擾動。混沌是在確定性系統中存在的隨機情況，表現為類似隨機的非隨機運動現象，其具有規律性、遍歷性、隨機性等特點。本文在初始化信息素階段應用Logistic 混沌映射。Logistic 混沌映射方程：

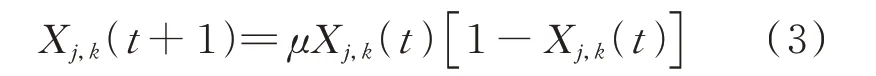
式中：X()為混沌變量；為控制變量。

當=4，0 ≤X(0)≤1 時，式（3）處 于 混 沌狀態。

信息素中引入Logistic 混沌映射：

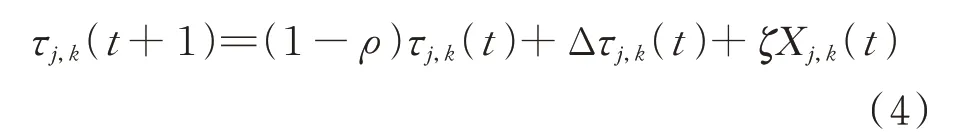
式中：為可調節參數。

2.3 多航跡選擇策略

在ACO 算法中，狀態轉移規則直接影響了搜索解的質量和效率，將真實螞蟻在前進中對信息素利用、對新航跡的探索以及一些“隨機行為”引入狀態轉移規則，采用多航跡選擇策略對基本狀態轉移規則進行改進，公式為

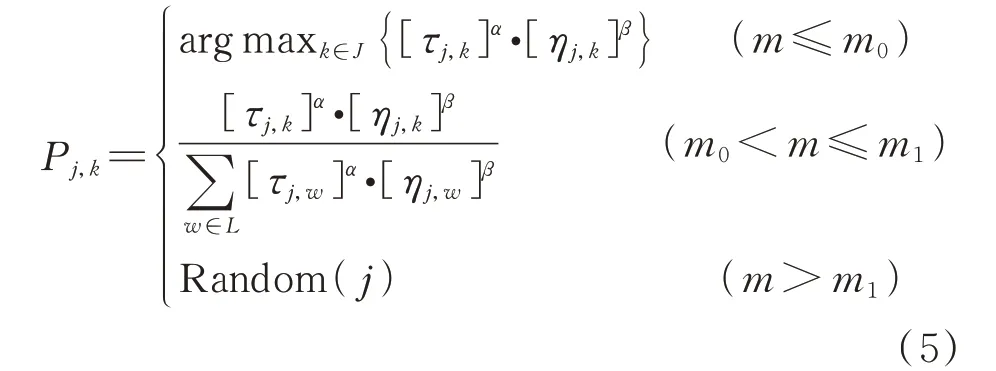
式 中：，為 常 數 且0 ＜＜1，0 ＜＜1；為隨機數且0 ＜＜1。

當≤時，從 可 行 航 跡 點 中 找 出[τ]·[η]最 大 的 航 跡 點；當＜≤時，使 用ACO 算法的狀態轉移規則選擇航跡點；當＞時，隨機選擇下一個航跡點。這種設計很好地保證了解的多樣性，同時避免算法因收斂速度快而陷入局部最優的情況。

2.4 模擬退火算法

Metropolis 研究發現一般組合優化問題和固體物質退火過程中物理系統的能量變化具有相似性，進而提出了模擬退火優化算法。固體物質退火分為升溫、等溫、降溫三個階段，高溫階段固體升溫，內能增加，固體內的粒子無序運動速度快，此過程與算法設置的初始溫度對應；等溫階段固體與外界保持熱平衡狀態，此過程與算法設置Me?tropolis 抽樣準則對應；退火階段固體溫度降低、內能減小，粒子趨于有序，最終達到穩定狀態，此過程與算法控制參數減小相對應。使用Metropolis抽樣準則接受一定條件下的劣解，有效避免陷入局部最優，以達到收斂全局最優解的效果。模擬退火算法流程如下：

（1）初始化：設置系統溫度為，初始溫度(0)=，任取初始解，確定每個時的迭代次數，即Metropolis 鏈長。

（2）對當前溫度和=1，2，…，，重復步驟（3）～步驟（6）。

（3）對當前解進行隨機擾動，得到新解；

（4）設置增 量 為d，d=()-()，為的代價函數。

（5）根據Metropolis 準則，公式為

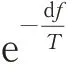
（6）當連續多個Metropolis 鏈中都未接受新解，或退火達到終止溫度，輸出當前解為最優解，然后結束；否則減小溫度后返回步驟（2）。

2.5 算法步驟

IH-ACO 算法通過Dijkstra 算法初始航跡、Lo?gistic 混沌映射初始化信息素、采用多航跡選擇策略和模擬退火機制，在提高算法收斂速度的同時，能夠有效提高全局搜索能力，避免陷入局部最優。改進算法流程如圖3 所示，具體實施步驟為：

（1）使用鏈接圖法構造二維空間環境模型；

（2）采用Dijkstra 算法規劃一條從起始點到終止點的初始航跡；

（3）初始化算法參數；

（4）引入Logistic 混沌映射，按照式（4）初始化信息素；

（5）設=0，只螞蟻放于初始點；

（6）蟻群算法開始搜索，根據式（5）選擇下一節點；

（7）判斷螞蟻是否到達終止點，若未到達終止點，跳轉至步驟（6），到達終止點則跳轉至步驟（8）；

（8）引入模擬退火機制，根據式（6）產生新解并更新最優解；

（9）根據當前航跡規劃情況，更新信息素；

（10）=+1，當＞時，輸出結果，否則跳轉至步驟（5）。

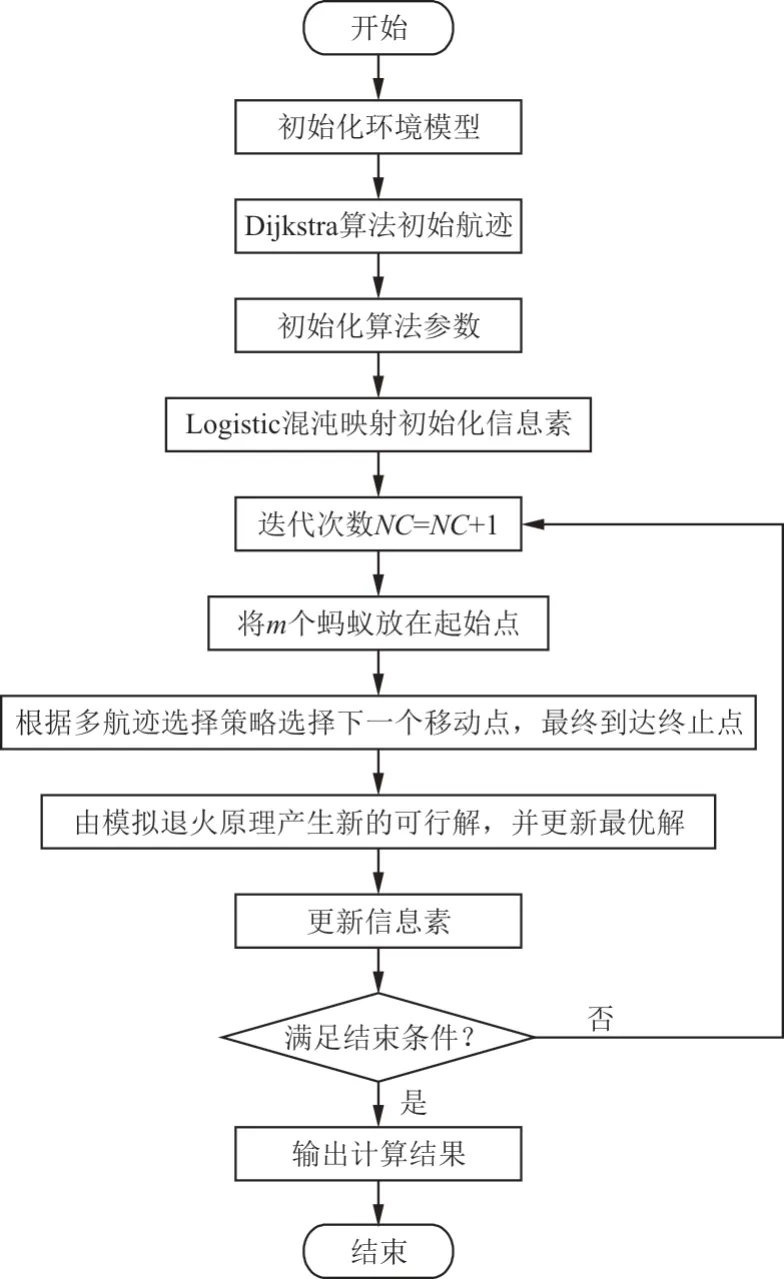
圖3 IH-ACO 算法流程圖Fig.3 IH-ACO flow diagram

3 仿真分析

為測試IH-ACO 算法在無人機作戰中飛行穿越地形障礙、躲避敵方地對空導彈威脅的航跡規劃效果，使用MATLAB 2018a 對IH-ACO 算法進行仿真，并與ACO 算法、文獻［10］的改進算法（Novel Ant Colony Algorithm，簡稱NL-ACO）和文獻［12］的改進算法（Evolutionary Ant Colony Al?gorithm，簡稱EY-ACO）在相同測試環境下進行對比。構造200 km×200 km 的二維仿真測試區域，進行算法參數初始化：種群數量=20，信息啟發因子＝1，期望啟發因子＝2，初始條件下信息素濃度＝0.000 09，信息素衰減因子＝0.5，隨機概率＝0.6，迭代次數=500，模擬退火初始溫度=90 ℃，終止溫度=10 ℃，退火系數為0.9，隨機產生地形障礙區（不規則多邊形表示）和敵方地空導彈威脅區（正方形表示）、起始點Start 和終止點End。

仿真實驗1：無人機穿越1 個的地形障礙區，初始點為Start（20，20）、終止點為End（140，90），實驗結果如圖4 所示。

圖4 一個地形障礙區時航跡軌跡迭代圖Fig.4 Iterative map of track in a terrain obstacle area

仿真實驗2：無人機穿越2 個地形障礙區，初始點為Start（20，180）、終止點為End（160，97），實驗結果如圖5 所示。

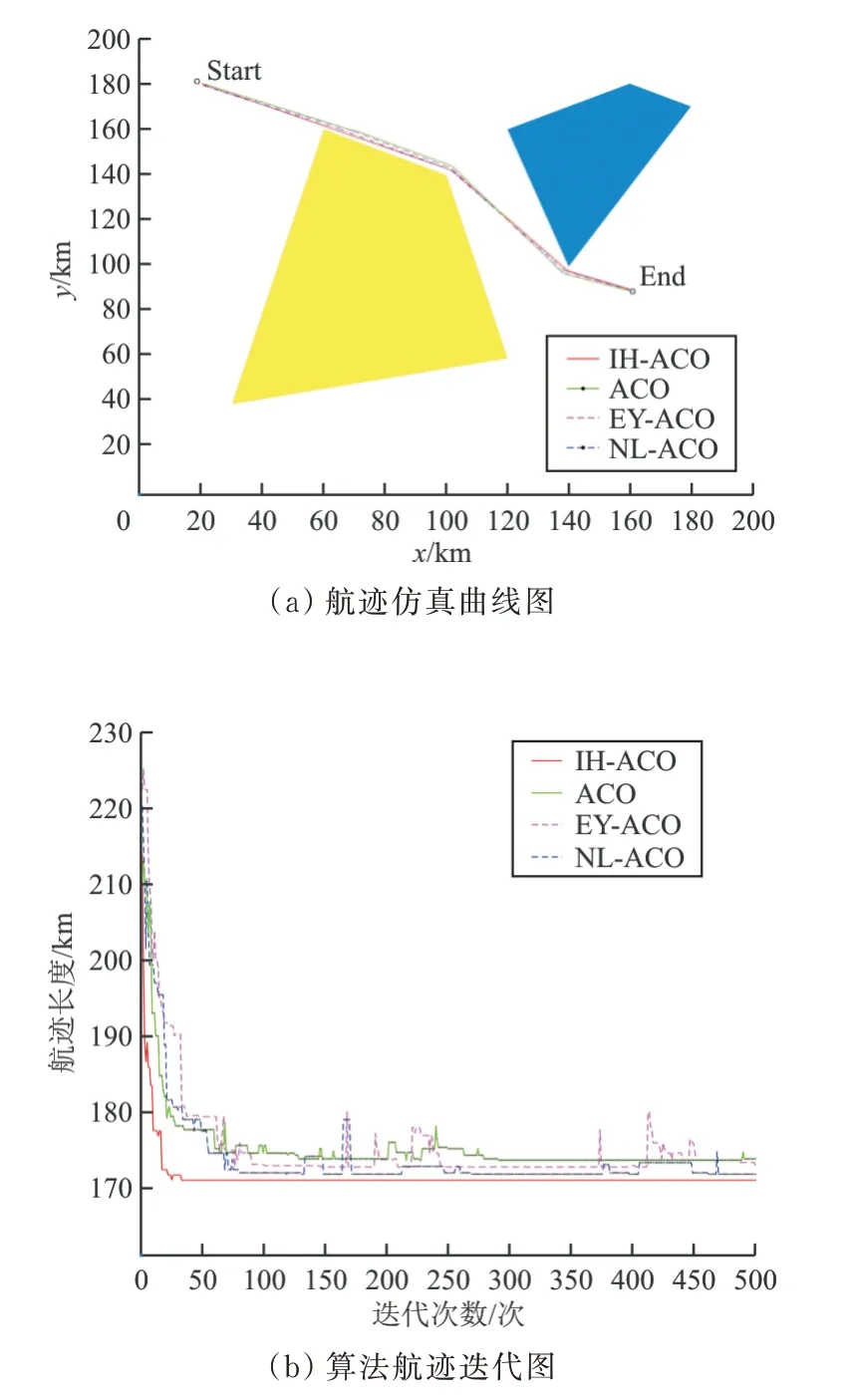
圖5 兩個地形障礙區時航跡軌跡迭代圖Fig.5 Iterative map of track in two terrain obstacle areas

仿真實驗3：無人機躲避1 個地空導彈威脅區并穿越3 個地形障礙區，初始點為Start（30，100）、終止點為End（180，60），實驗結果如圖6 所示。

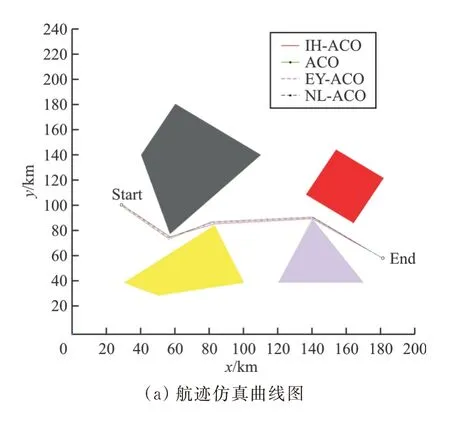
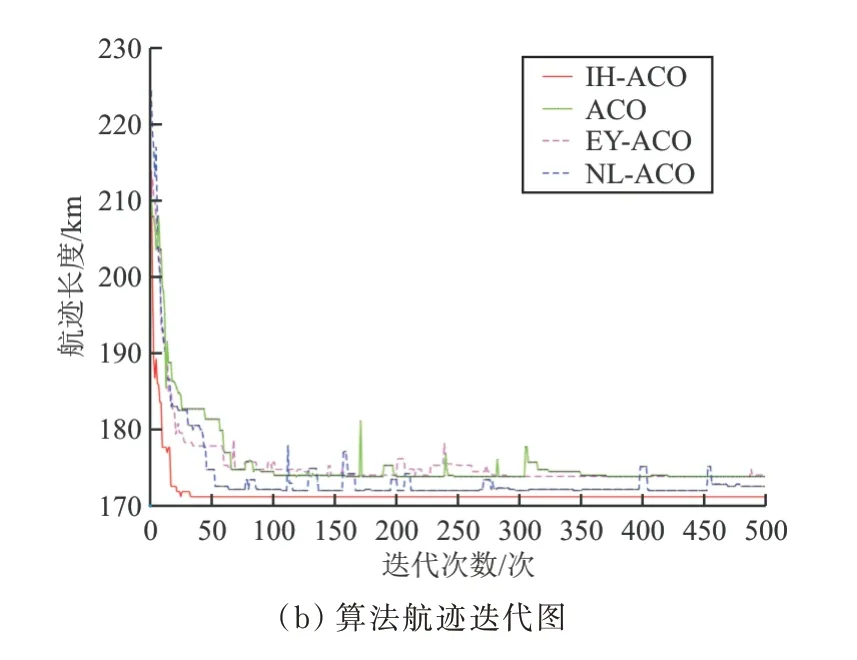
圖6 1 個地空導彈威脅區和3 個地形障礙區時航跡軌跡迭代圖Fig.6 Iterative map of track trajectory for one surface to air missile threat area and three terrain obstacle areas

仿真實驗4：無人機穿越躲避3 個地空導彈威脅區并穿越5 個地形障礙區，初始點為Start（10，100）、終 止 點 為End（180，80），實 驗 結 果 如 圖7所示。

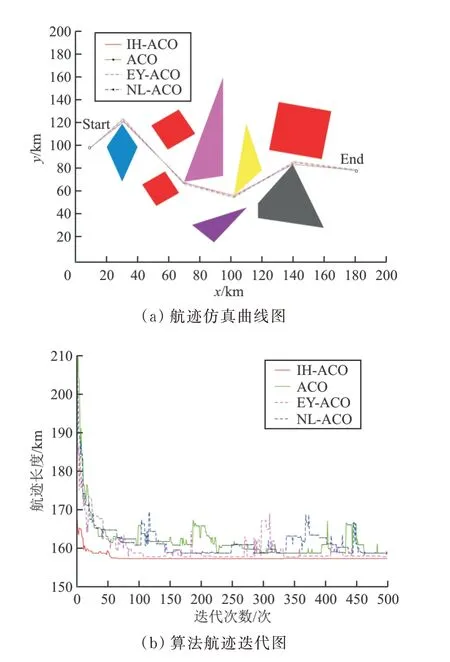
圖7 3 個地空導彈威脅區和5 個地形障礙區時航跡軌跡迭代圖Fig.7 Iterative map of track trajectory for three surface to air missile threat areas and five terrain obstacle areas

從圖4～圖7 中的（a）圖可以看出：在無人機航跡規劃過程中，通過使用ACO 算法、NL-ACO 算法、EY-ACO 算法、IH-ACO 算法，無人機可以有效穿越地形障礙、躲避敵方地對空導彈威脅，證明四種算法都能滿足無人機航跡規劃的基本要求。

從圖4～圖7 中的（b）圖可以看出：IH-ACO 算法和ACO 算法相比，在迭代次數一定的情況下，IH-ACO 算法搜索得到的最短航跡更小，表明本文改進算法的全局搜索能力得到了增強；IH-ACO算法與NL-ACO 算法、EY-ACO 算法相比，在均可加快收斂速度的情況下，NL-ACO 算法、EYACO 算法在面對復雜環境時出現了停滯在局部最優解的情況，而本文改進算法仍可以很好地進行航跡搜索。綜上所述，可以證明IH-ACO 算法可有效解決全局尋優與收斂速度之間矛盾。

四種算法運算結果如表1 所示，可以看出：IHACO 算法在最短航跡、收斂時間上都要優于其他三種算法，表明IH-ACO 算法在精度提高的同時，加快了收斂速度，即IH-ACO 算法具有更好的尋優能力。

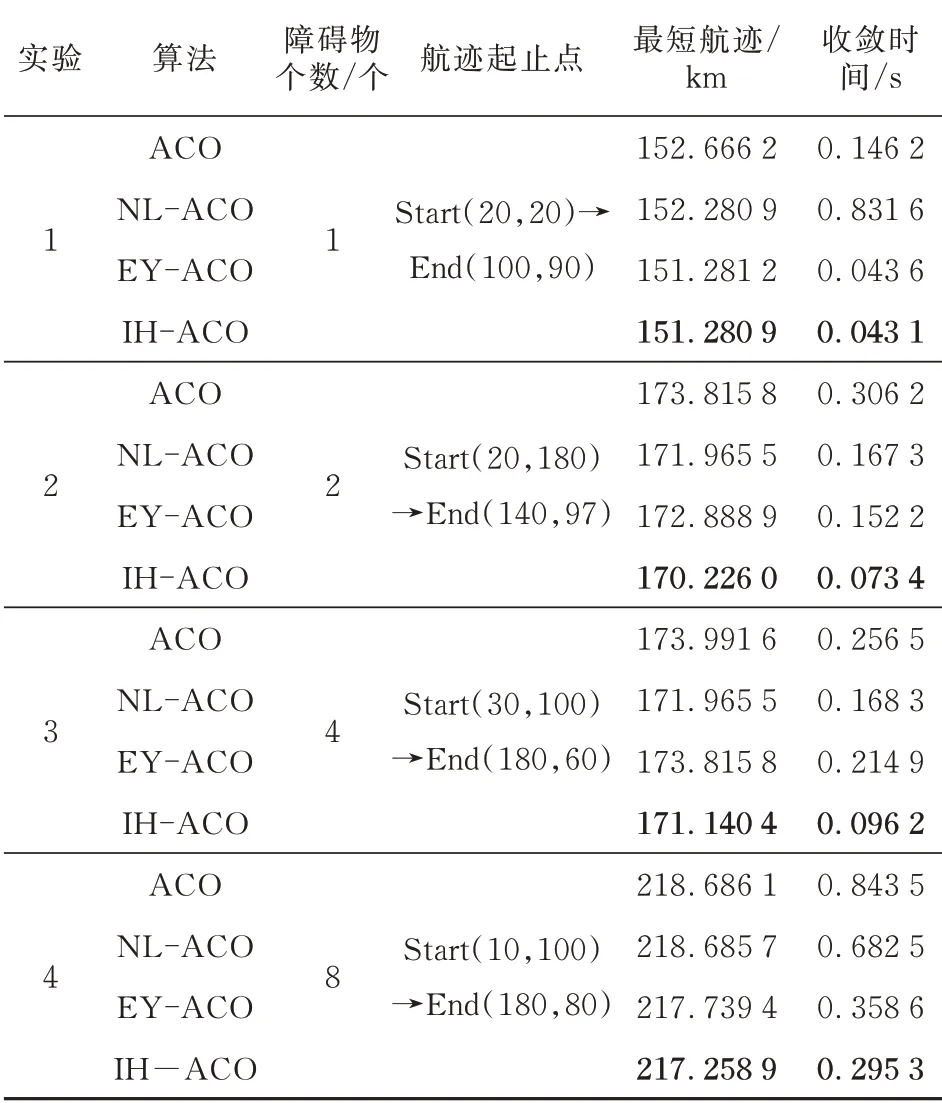
表1 四種算法運算結果Table 1 Calculation results of four algorithms

綜上可知，由于在前期進行了Dijkstra 算法初始航跡、Logistic 混沌映射初始化信息素，在中、后期采用多航跡選擇策略和模擬退火機制，IH-ACO算法加強了全局搜索能力并提高了算法收斂速度，相比ACO 算法具有更好的航跡規劃效果。

4 結 論

（1）使用Dijkstra 算法進行初始化航跡、Logis?tic 混沌映射初始化信息素，保證較快的搜索速度，提高蟻群前期搜索能力。

（2）采用多航跡選擇策略的狀態轉移規則，增加解的多樣性，有效提高了算法的全局搜索能力。

（3）應用模擬退火機制，避免算法收斂過快陷入局部最優解。

（4）IH-ACO 算法在航跡規劃過程中，因Dijk?stra 初始化和Logistic 初始化能加快前期搜索效率、多航跡選擇策略能增加解的多樣性、模擬退火機制能防止早熟收斂，有效解決全局尋優與收斂速度之間的矛盾，在無人機作戰的航跡任務規劃中有很好的適用性。

（5）HI-ACO 算法與ACO 算法相比，在收斂速度提升的同時保證了全局搜索能力；HI-ACO算法與NL-ACO 算法、EY-ACO 算法相比，在復雜環境中仍能快速、有效地進行航跡搜索，解決了其他改進算法在復雜環境中停滯在局部最優解的問題。

下一步將研究如何將IH-ACO 算法應用到有更多約束條件的復雜環境中進行航跡規劃，并結合不同的作戰環境和目的要求，提出更實時高效的航跡規劃算法。