基于傾向性評分簡單加權估計的慢性乙型肝炎抗病毒治療的成本?效果分析

陳舸，楊朔，周峰，李麗霞，周舒冬，賈衛東，郜艷暉3，

（1.廣東藥科大學公共衛生學院，廣東 廣州 510310；2.廣州市第八人民醫院信息科，廣東 廣州 510080；3.暨南大學基礎醫學與公共衛生學院，廣東 廣州 510270）

藥物經濟學研究中常用成本?效果分析（cost?effectiveness analysis,CEA）來評價不同藥物治療效果的優劣[1]，對臨床用藥和藥品政策的制定都能起到參考作用。通常采用隨機對照臨床試驗、前瞻性隊列研究、回顧性隊列研究以及二次文獻研究進行分析。《中國藥物經濟學評價指南》指出，回顧性隊列研究的有關數據大多可以從現有的數據庫獲得、研究成本較低，且研究時間較短。因此，回顧性隊列研究是缺乏前瞻性研究時的最佳選擇[1]。然而，回顧性隊列研究中由于患者的非隨機選擇導致的組別間疾病特征和治療方案的差異，以及醫療費用數據的刪失等問題給成本?效果分析帶來困難。

觀察性研究中，費用數據由于患者出現刪失，通常是不完整的。Lin等[2]指出，由于生存數據的費用不是非信息刪失（non?informatively cencored），即刪失成本與潛在未刪失成本之間不相互獨立，傳統處理刪失生存數據的方法不再有效地用于分析刪失成本數據。此外，由于出現刪失，除非有更多的假設，否則無法估計整個健康史的成本和生存分布。因此，通常需要設置有限的時間范圍，例如L年。Bang和Tsiatis[3]提供了生存數據成本估計的方法，即簡單加權法。簡單加權的方法是使用未刪失的觀測數據的費用信息，通過計算該時期無刪失的逆概率權重，對每個具有完整數據的觀測進行加權，從而對時間范圍內的平均生存費用進行估計。另外，為了控制組間存在的混雜，可以采用傾向評分（propensity score，PS）的方法。該方法由Rosenbaum和Rubin[4]首先提出的。基于傾向評分，可以通過匹配、分層、加權和回歸等方式對混雜因素調整。其中，逆概率加權（inverse probability of treatment weighting，ⅠPTW）[5]已成為首選方法。該方法利用傾向得分這個權重構造一個虛擬樣本，使各處理組間基線協變量分布均衡，從而不同組間的結果能夠進行比較。目前國內采用觀察性數據進行成本?效果分析的研究仍較少，希望通過本文的研究能對今后該方法在國內的應用提供參考。

1 原理與方法

1.1 傾向性評分簡單加權法

假定一多組獨立有刪失生存數據，L為估計成本的時間范圍，Yi（u）為到u時期的累計成本，Yi為在時間范圍L內累計總成本。Ci為刪失時間，設研究有i個觀測對象，令ti為每個觀測對象的生存時間，其中變量t受時間范圍L限制。其中L可以根據需要進行設定，例如我們想要了解觀測壽命年的成本。基于上述的設定，可以得到以下的參數：

Ti=min（ti,Ci）為觀測在時間范圍內的隨訪時間，且Ti=min（Ti,L）；

δi=I（ti≤Ci）表示出現結局的指示變量，當δi=1時表示第i個觀測的結局可以被觀測；

Yi=Yi（ti）為δi=1的所有觀測的總費用；

Zi=0，1，2，…，K表示有K個組別，Xi為協變量向量。

令K（u）=Pr（C≥u）表示觀測在u時刻無刪失的概率，其中K（u）可以從參數模型或非參數模型來估計得到。這里使用Kaplan?Meier估計來估計K（u）。

令pik為第i觀測成為k組的概率，pik=P（Zi=k|Xi），即為傾向性評分值。本文采用logistic回歸模型估計傾向性評分，進一步計算ⅠPTW權重。ⅠPTW權重可分為非穩定權重和穩定權重。非穩定權重定義為穩定權重定義為，本文采用穩定權重進行加權。其中pt為K組別占總樣本的比例。由此可得到平均費用：

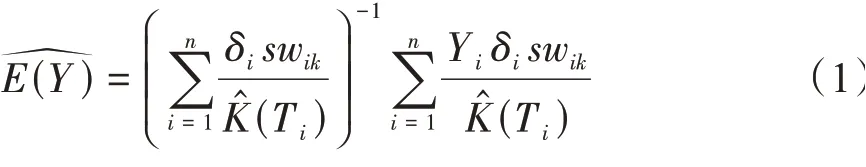
在時間范圍L內的平均生存時間可以通過生存函數曲線下面積來計算。為S（u）=Pr（T≥u）的估計值。然而，這個方法需要非信息性刪失，并且不對混雜因素進行調整。Willan和Briggs[6]建議使用估計費用的加權方法來替代生存曲線下面積來計算生存時間（效果）。所以在這里，我們應用與估計成本費用相同的概念來估計：

根據上述公式，假設Z=1表示某治療策略，Z=0表示某參照策略，我們可達到ΔC和ΔE為：

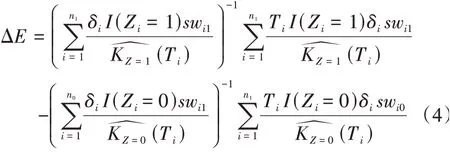
1.2 成本?效果分析方法

（1）增量成本效果比（ⅠCER）

成本?效果分析采用的評價指標為成本?效果比（cost?effectiveness ratio,CER），是將成本（cost,C）作為分子，效果（effectiveness,E）作為分母，計算兩者的比值CER=C/E，由此可以獲得單位效果所需的成本[1]。

當運用成本?效果分析方法對多個方案進行評價與方案選擇時，需要使用增量分析法，其指標為增量成本?效果比（incremental cost?effectiveness ratio,ⅠCER）。ⅠCER是指兩種方案之間的增量成本除以增量健康產出，表示增加一個單位的健康產出所消耗的增量成本，可用于評價兩個或兩個以上治療方案之間的相對經濟性。增量成分?效果比用式（5）表示：

運用增量效果比的判斷標準為：如果一個治療方案相對于另一個方案的ⅠCER低于某個特定價值標準，即人們意愿支付值（willingness to pay,WTP）（常用λ表示），則表示該方案經濟性更優。根據世界衛生組織的建議[1]，如果新的治療策略額外獲取一個效果所付出的額外成本低于3倍國內人均生產總值（gross domestic product,GDP），則認為該治療策略是可以被患者接受的。因此，本研究將人們意愿支付的值設定為2016年的3倍國內人均GDP（155 594元/年）

（2）凈效益值（NMB）

現階段，衛生經濟研究提倡使用凈效益值（net?monetary?benefit,NMB）來對藥物的成本?效果進行評價[1]：

NMB是ΔC和ΔE的線性組合，用來測量在給定人們意愿支付的值λ的水平下的超額收益。

1.3 置信區間計算和概率敏感性分析

采用Bootstrap方法計算ⅠCER和NMB的置信區間。Bootstrap是一個非參數方法，利用概率理論從研究中得到樣本的點估計值的置信區間。一般步驟為采用放回抽樣的方法，從研究樣本中抽取觀測組成Boots樣本，通過重復抽取n次（本研究抽取1 000次），進而得到參數5%~95%的可信區間范圍，這可以使研究者得到不同治療方案的所有可能性和極端情況[7?8]。概率敏感性分析結果用成本?效果可接受曲線表示。成本?效果可接受曲線顯示在人們意愿支付閾值下，某一種治療方案成為最優治療策略的概率是多少。

2 實例分析

2.1 數據來源

本研究數據來源于廣州市最大的傳染病專科醫院。從醫院電子病歷系統中確認2008－2016年間診斷為慢性乙型肝炎（以下簡稱慢乙肝）、肝硬化和肝癌的所有門診及住院患者，提取其門診系統、住院系統和檢驗系統中相關信息，包括就診時間、診斷、處方、費用和所有檢驗信息。

2.2 研究內容

本研究為回顧性隊列研究。觀察起點為慢乙肝初治患者開始抗病毒治療時間，收集患者的人口學信息（性別、年齡等）、就診信息（就診時間、疾病診斷等）、抗病毒用藥信息，包括干擾素（interferon,ⅠFN）、恩替卡韋（entecavir,ETV）、拉米夫定（lamivu‐dine,LAM）、阿德福韋酯（adefovirdipivoxil,ADV）、替比夫定（telbivudine,LdT）、實驗室檢查信息（HBV DNA、ALT水平及乙肝兩對半檢查結果等）、費用信息（抗病毒藥費、其他藥費、檢驗檢查費、床位護理費、其他費用等）。如果患者出現疾病進展，則以發生該終點日期為終止時間。其中，疾病進展定義為發生肝硬化或肝癌。如果患者在隊列終止前（2016年12月31日）未觀察到疾病進展情況，則定義為刪失。刪失患者的觀察終點為患者末次就診時間。生存時間定義為患者首次抗病毒用藥到觀察終止所經歷的時間。本研究使用無疾病進展生存時間（年）（progression?free survival,PFS）作為衡量疾病治療效果的指標，使用總醫療費用作為疾病治療成本的指標，并采用5%貼現率對費用進行貼現。

2.3 統計分析

本研究使用SAS 9.4軟件對人口學資料進行描述，使用PROC LOGⅠSTⅠC過程進行傾向性評分估計，使用PROC LⅠFETEST過程進行簡單加權權重估計。根據相關公式，編寫協變量調整簡單加權后的成本?效果分析估計以及Bootstrap的SAS程序。

3 結果

研究納入1 626名慢乙肝初治患者，各組患者基線特征如表1所示，各組間基線年齡、性別、HBV DNA水平、HBeAg水平分布差異均有統計學意義。通過對各治療組進行逆概率加權，使基線的混雜因素在各治療組間的分布達到了平衡（表2）。這說明加權后各治療組之間是可比的，解決了觀察性研究中因非隨機化分組而帶來的混雜。

表1 不同抗病毒用藥患者的基線特征Table 1 Characteristics of patients with different antiviral drugs

表2 逆概率加權后不同抗病毒用藥患者的基線特征Table 2 Characteristics of patients with different antiviral drugs after inverse probability weighting

表3為不同治療組的年直接費用結果。費用的均數大于中位數。其中ⅠFN組的年平均總費用最高，達到了9 567.41元，其次是ETV（6 258.83元）和ETV+ADV組（6 038.46元），年平均總費用最低的是ADV組（3 825.62元）。

表3 不同抗病毒用藥患者的年直接醫療費用（元）Table 3 Annual direct medical expenses of patients with different antiviral drugs

基于傾向性評分簡單加權法，估計各治療組在3、5、8年治療效果、治療成本、增量效果、增量成本，結果如表4所示。ⅠFN組在3年、5年和8年均獲得最好的效果，同時總成本也是最高的。在核苷（酸）類似物（NAS）方案中，LAM+ADV組則獲得了最高的效果，其次為ETV+ADV聯合治療方案。

表4 不同抗病毒用藥患者療效與成本的估計Table 4 Estimation of effectiveness and total cost of different antiviral treatment in chronic hepatitis patients

以ADV組作為參比，各治療組在3、5、8年成本?效果分析結果如表5。3年總費用的成本?效果分析結果顯示：LAM組與ADV相比獲得更低的效果和更高的費用，處于絕對劣勢。在意愿支付閾值下，ADV比LdT更具擴展優勢。ⅠFN產生的ⅠCER（223 626.00元/年）遠遠高于意愿支付的閾值，ETV、ETV+ADV、LAM+ADV 3種治療方案所產生的ⅠCERs（ETV：26 534.63元/年，ETV+ADV：36 031.42元/年，LAM+ADV：28 231.21元/年）都低于意愿支付的閾值。進一步的計算凈效益值發現，在這3種治療方案中，LAM+ADV（17 830.79元）治療方案的凈效益估計結果均高于ETV（10 324.75元）和ETV+ADV組（14 347.51元）。5年總費用的成本?效果分析結果顯示：LAM產生的ⅠCER（142 614.00元/年）處于意愿支付閾值的臨界。另外ⅠFN、LdT、ETV、ADV+ETV、LAM+ADV所產生的ⅠCERs都低于意愿支付的閾值。進一步的計算凈效益值發現，LAM+ADV（50 337.06元）治療方案的凈效益估計結果最高，這提示了LAM+ADV治療方案對其他治療方案占據了優勢。8年總費用的成本?效果分析結果顯示：LAM、LdT和ETV治療方案與ADV組相比效果更好，成本更低，處于絕對優勢。另外ⅠFN、ETV+ADV、LAM+ADV 3種治療方案所產生的ⅠCERs都低于意愿支付的閾值。進一步的計算凈效益值發現，ⅠFN（167 361.60元）治療方案的凈效益估計結果最高，其次為LAM+ADV（159 304.60元）治療方案。

表5 不同抗病毒用藥患者總費用的成本?效果分析Table 5 Cost?effectivenessof different antiviral treatment in chronic hepatitis patients

總費用可接受曲線結果顯示，在人們意愿支付閾值下，接受治療3年，LAM+ADV聯合治療方案成為成本?效果最優方案的概率最大，高達80.7%；接受治療5年，LAM+ADV聯合治療方案成為成本?效果最優方案的概率最大（55.7%）；接受治療8年，ⅠFN單藥治療方案成為成本?效果最優方案的概率最大（52.0%），見圖1~圖3。

圖1 3年治療的成本?效果可接受曲線Figure1 Cost?effectivenessacceptability curveof 3?year treatment

圖3 8年治療的成本?效果可接受曲線Figure3 Cost?effectivenessacceptability curveof 8?year treatment

4 討論

針對真實世界數據存在的偏倚問題，除了設計科學合理的研究方案，在統計分析階段還應采用合理的分析方法進行處理。本研究采用傾向性評分逆概率加權的方法對觀測數據中的潛在混雜進行調整。該方法通過對多個協變量綜合成一個得分值，進而構造出一個加權樣本，能夠很好解決傳統方法無法處理的由協變量過多而導致的過度匹配、過度分層以及共線性等問題[9?10]，從而最大限度地減少混雜的偏倚。逆概率加權的權重設定包括了非穩定權重和穩定權重，由于非穩定權重會使樣本量膨脹，容易出現極值，導致結局不穩定[11]。因此，本文中使用穩定化權重的方法進行加權調整，該計算方式保留了原始人群一樣的樣本量，減少極值的出現，減小了Ⅰ類錯誤。但逆概率加權的方法也存在無法處理未測量的混雜，要求在協變量不同水平下的不同分組均要有觀測等問題。另外，雖然逆概率加權能夠處理多個混雜因素，但并不是說能夠隨意選擇協變量加入模型。過多或錯誤的選擇協變量則會產生偏倚，從而導致權重的估計錯誤。

對于刪失數據，可以通過排除發生刪失的數據或把刪失數據當作完整數據的簡單方式進行處理。但是這些做法會造成受試者信息丟失、估值偏低等問題。本文采用了簡單加權方法，假設刪失為完全隨機缺失（missing completely at random,MCAR）的數據，即認為受試者發生刪失的原因與其他因素無關，出現刪失的受試者與未出現刪失的受試者的成本或療效是相似的，因而可以利用未刪失受試者的成本或療效來估計刪失受試者的成本或療效[12]。然而本研究并未考慮利用刪失受試者已有的成本或療效進行估計，以及當其他混雜因素與發生刪失存在關聯，即該刪失類型為隨機缺失（missing at random,MAR）時如何對刪失進行處理和估計。今后的研究可以對成本或療效的方法進一步優化。

目前，藥物經濟學越來越受到重視，本文將基于傾向性評分簡單加權估計的方法應用于慢乙肝抗病毒治療的成本?效果分析中，研究發現干擾素治療方案在短期治療（3年和5年）上不具有成本?效果，但在長期治療（8年）上是成本?效果最優的治療方案；在NAS治療方案中，LAM+ADV初始聯合治療方案在3年、5年和8年的治療中最具成本?效果。基于本研究結果，對慢性乙型肝炎患者的抗病毒藥的成本以及療效有了更全面的了解，為醫生對慢性乙型肝炎初治患者選擇合適的治療方案提供了參考，也為“真實世界”復雜醫療數據的長期療效比較和成本?效果的實證分析提供了方法選擇。

圖2 5年治療的成本?效果可接受曲線Figure2 Cost?effectivenessacceptability curveof 5?year treatment